Rumus Gerak Fisika

Suatu benda dikatakan bergerak apabila kedudukan atau posisinya berubah terhadap acuan tertentu. Titik-titik berurutan yang dilalui oleh benda yang bergerak disebut lintasan. Gerak dengan lintasan berbentuk garis lurus disebut gerak lurus. Dibawah ini adalah rumus gerak fisika:

Gerak lurus beraturan

Sistem koordinat kutub dua dimensi

Gerak Lurus Beraturan (GLB) adalah suatu gerak lurus yang mempunyai kecepatan konstan. Maka nilai percepatannya adalah a = 0. Gerakan GLB berbentuk linear dan nilai kecepatannya adalah hasil bagi jarak dengan waktu yang ditempuh.

Rumus gerak lurus beraturan:

$\!v={\frac {s}{t}}$

Dengan ketentuan:

$\!s$ = Jarak yang ditempuh (km, m)
$\!v$ = Kecepatan (km/jam, m/s)
$\!t$ = Waktu tempuh (jam, sekon)

Catatan:

Untuk mencari jarak yang ditempuh, rumusnya adalah $\!s=\!v\times \!t$ .
Untuk mencari waktu tempuh, rumusnya adalah $\!t={\frac {s}{v}}$ .
Untuk mencari kecepatan, rumusnya adalah $\!v={\frac {s}{t}}$ .
Jadi: 1 m/s = 3,6 km/jam

Kecepatan rata-rata

Rumus:

$\!v={\frac {s_{total}}{t_{total}}}={\frac {V_{1}\times t_{1}+V_{2}\times t_{2}+...+V_{n}\times t_{n}}{t_{1}+t_{2}+...+t_{n}}}$

Gerak Lurus Berubah Beraturan

Gerak lurus berubah beraturan adalah gerak yang lintasannya berupa garis lurus dengan kecepatannya yang berubah beraturan.

Percepatannya bernilai konstan/tetap.

Rumus GLBB ada 3, yaitu:

$\!v_{t}=\!v_{0}+\!a\times \!t$
$\!s=\!v_{0}\times \!t+{\frac {1}{2}}\times \!a\times \!t^{2}$

$\!v_{t}^{2}=\!v_{0}^{2}+\!2\times \!a\times \!s$

Dengan ketentuan:

$\!v_{0}$ = Kecepatan awal (m/s)
$\!v_{t}$ = Kecepatan akhir (m/s)
$\!a$ = Percepatan (m/s²)
$\!s$ = Jarak yang ditempuh (m)

Gerak vertikal ke atas

Benda dilemparkan secara vertikal, tegak lurus terhadap bidang horizontal ke atas dengan kecepatan awal tertentu. Arah gerak benda dan arah percepatan gravitasi berlawanan, gerak lurus berubah beraturan diperlambat.

Peluru akan mencapai titik tertinggi apabila V_t sama dengan nol.

$t_{\text{maks}}={\frac {Vo}{g}}$

$h={\frac {Vo^{2}}{2g}}$

$t={2}\times {t_{\text{maks}}}$

${V_{\text{t}}^{2}}=V_{\text{0}}^{2}-2\times {g}\times {h}$

Keterangan:

Kecepatan awal= Vo
Kecepatan benda di suatu ketinggian tertentu= Vt
Percepatan /Gravitasi bumi: g
Tinggi maksimum: h
Waktu benda mencapai titik tertinggi: t _maks
Waktu ketika benda kembali ke tanah: t

Catatan gerak vertikal keata:

$t_{titiktertinggi}={\frac {v_{0}}{g}},t_{kembalikeawal}={\frac {2v_{0}}{g}}$

$h_{maks}={\frac {{v_{0}}^{2}}{2g}}$

Gerak jatuh bebas

Benda dikatakan jatuh bebas apabila benda:

Memiliki ketinggian tertentu (h) dari atas tanah.
Benda tersebut dijatuhkan tegak lurus bidang horizontal tanpa kecepatan awal.

Selama bergerak ke bawah, benda dipengaruhi oleh percepatan gravitasi bumi (g) dan arah kecepatan/gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.

$v={\sqrt {2gh}}$

$t={\sqrt {2h/g}}$

Keterangan:

v = kecepatan di permukaan tanah
g = gravitasi bumi
h = tinggi dari permukaan tanah
t = lama benda sampai di tanah

Gerak vertikal ke bawah

Benda dilemparkan tegak lurus bidang horizontal arahnya ke bawah.

Arah percepatan gravitasi dan arah gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.

$Vt={Vo}+g\times t$

$Vt^{2}={Vo^{2}}+2\times g\times h$

Keterangan:

Vo = kecepatan awal
Vt = kecepatan pada ketinggian tertentu dari tanah
g = gravitasi bumi
h = jarak yang telah ditempuh secara vertikal
t = waktu

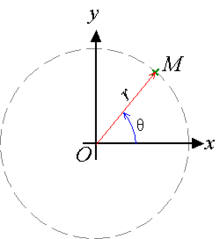
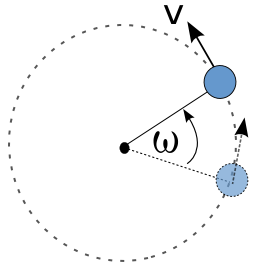
Gerak Melingkar atau Gaya Sentripetal

Gerak dengan lintasan berupa lingkaran.

Dari diagram di atas, diketahui benda bergerak sejauh ω° selama $t$ sekon, maka benda dikatakan melakukan perpindahan sudut.

Benda melalukan 1 putaran penuh. Besar perpindahan linear adalah $2\pi r$ atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah $2\pi$ radian atau 360°.

$2\pi rad=360^{\circ }$

$1rad={\frac {360^{\circ }}{2\pi }}={\frac {180^{\circ }}{\pi }}=57,3^{\circ }$

Perpindahan sudut, kecepatan sudut dan percepatan sudut

Perpindahan sudut adalah posisi sudut benda yang bergerak secara melingkar dalam selang waktu tertentu.

$\theta =\omega \times t$

Keterangan:

$\theta$ = perpindahan sudut (rad)
$\omega$ = kecepatan sudut (rad/s)
t = waktu (sekon)

Kecepatan sudut rata-rata ( ${\overline {\omega }}$ ): perpindahan sudut per selang waktu.

${\overline {\omega }}={\frac {\vartriangle \theta }{\vartriangle t}}={\frac {\theta _{2}-\theta _{1}}{t_{2}-t_{1}}}$

Percepatan sudut rata-rata ( $\alpha$ ): perubahan kecepatan sudut per selang waktu.

$\alpha ={\frac {\vartriangle \omega }{\vartriangle t}}={\frac {\omega _{2}-\omega _{1}}{t_{2}-t_{1}}}$

$\alpha$ : Percepatan sudut (rad/s²)

Percepatan sentripetal

Arah percepatan sentripetal selalu menuju ke pusat lingkaran.

Percepatan sentripetal tidak menambah kecepatan, melainkan hanya untuk mempertahankan benda agar tetap bergerak melingkar.

$A_{s}={\frac {v^{2}}{r}}=\omega ^{2}r$

Keterangan:

r : jari-jari benda/lingkaran
A_s: percepatan sentripetal (rad/s²)

Gerak melingkar beraturan

Ciri-ciri gerak melingkar beraturan:

Besar kelajuan linearnya tetap
Besar kecepatan sudutnya tetap
Besar percepatan sentripetalnya tetap
Lintasannya berupa lingkaran

Gerak Melingkar Beraturan (GMB) adalah gerak melingkar dengan besar kecepatan sudut $\omega\!$ tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial $v_T\!$ dengan jari-jari lintasan $R\!$ .

\omega = \frac {v_T} R

Arah kecepatan linier $v\!$ dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial $v_T\!$ . Tetapnya nilai kecepatan $v_T\!$ akibat konsekuensi dar tetapnya nilai $\omega\!$ . Selain itu terdapat pula percepatan radial $a_R\!$ yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.

a_R = \frac {v^2} R = \frac {v_T^2} R

Bila $T\!$ adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran $\theta = 2\pi R\!$ , maka dapat pula dituliskan

v_T = \frac {2\pi R} T \!

Kinematika gerak melingkar beraturan adalah

\theta(t) = \theta_0 + \omega\ t

dengan $\theta(t)\!$ adalah sudut yang dilalui pada suatu saat $\theta_0\!$ adalah sudut mula-mula dan $\omega\!$ adalah kecepatan sudut (yang tetap nilainya).

Gerak melingkar berubah beraturan

Gerak Melingkar Berubah Beraturan (GMBB) adalah gerak melingkar dengan percepatan sudut $\alpha\!$ tetap. Dalam gerak ini terdapat percepatan tangensial $a_T\!$ (yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial $v_T\!$ ).

\alpha = \frac {a_T} R

Kinematika GMBB adalah

\omega(t) = \omega_0 + \alpha\ t \!

\theta(t) = \theta_0 + \omega_0\ t + \frac12 \alpha\ t^2 \!

\omega^2(t) = \omega_0^2 + 2 \alpha\ (\theta(t) - \theta_0) \!

dengan $\omega_0\!$ adalah kecepatan sudut mula-mula.

Persamaan Parametrik (gerak melingkar)

Gerak melingkar dapat pula dinyatakan dalam persamaan parametrik dengan terlebih dahulu mendefinisikan:

titik awal gerakan dilakukan $(x_0,y_0)\!$
kecepatan sudut putaran $\omega\!$ (yang berarti suatu GMB)
pusat lingkaran $(x_c,y_c)\!$

untuk kemudian dibuat persamaannya.

Hal pertama yang harus dilakukan adalah menghitung jari-jari lintasan $R\!$ yang diperoleh melalui:

R = \sqrt{(x_0 - x_c)^2 + (y_0 - y_c)^2} \!

Setelah diperoleh nilai jari-jari lintasan, persamaan dapat segera dituliskan, yaitu

x(t)=x_{c}+R\cos(\omega t+\phi _{x})\!

y(t)=y_{c}+R\sin(\omega t+\phi _{y})\!

dengan dua konstanta $\phi_x \!$ dan $\phi_y \!$ yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai $(x_0,y_0)\!$ , maka dapat ditentukan nilai $\phi_x \!$ dan $\phi_y \!$ :

\phi_x = \arccos \left( \frac{x_0 - x_c}{R} \right)\!

\phi_y = \arcsin \left( \frac{y_0 - y_c}{R} \right)\!

Perlu diketahui bahwa sebenarnya

\phi_x = \phi_y \!

karena merupakan sudut awal gerak melingkar.

Hubungan antar besaran linier dan angular

Dengan menggunakan persamaan parametrik, telah dibatasi bahwa besaran linier yang digunakan hanyalah besaran tangensial atau hanya komponen vektor pada arah angular, yang berarti tidak ada komponen vektor dalam arah radial. Dengan batasan ini hubungan antara besaran linier (tangensial) dan angular dapat dengan mudah diturunkan.

Kecepatan tangensial dan kecepatan sudut

Kecepatan linier total dapat diperoleh melalui

v = \sqrt{v_x^2 + v_y^2}

dan karena batasan implementasi persamaan parametrik pada gerak melingkar, maka

v_T = v = \sqrt{v_x^2 + v_y^2}

dengan

v_x = \dot{x} = \frac{dx}{dt}

v_y = \dot{y} = \frac{dy}{dt}

diperoleh

v_x = -\omega R \sin(\omega t + \phi_x) \!

v_y = \omega R \cos(\omega t + \phi_x) \!

sehingga

v_T = \sqrt{(-\omega)^2 R^2 \sin^2(\omega t + \phi_x) + \omega^2 R^2 \cos^2(\omega t + \phi_x)}\!

v_T = \omega R \sqrt{\sin^2(\omega t + \phi_x) + \cos^2(\omega t + \phi_x)}\!

v_T = \omega R\!

Percepatan tangensial dan kecepatan sudut

Dengan cara yang sama dengan sebelumnya, percepatan linier total dapat diperoleh melalui

a = \sqrt{a_x^2 + a_y^2}

dan karena batasan implementasi persamaan parametrik pada gerak melingkar, maka

a_T = a = \sqrt{a_x^2 + a_y^2}

dengan

a_x = \ddot{x} = \frac{d^2x}{dt^2}

a_y = \ddot{y} = \frac{d^2y}{dt^2}

diperoleh

a_x = -\omega^2 R \cos(\omega t + \phi_x) \!

a_y = -\omega^2 R \sin(\omega t + \phi_x) \!

sehingga

a_T = \sqrt{(-\omega)^4 R^2 \cos^2(\omega t + \phi_x) + \omega^4 R^2 \sin^2(\omega t + \phi_x)}\!

a_T = \omega^2 R \sqrt{\cos^2(\omega t + \phi_x) + \sin^2(\omega t + \phi_x)}\!

a_T = \omega^2 R\!

Kecepatan sudut tidak tetap

Persamaan parametric dapat pula digunakan apabila gerak melingkar merupakan GMBB, atau bukan lagi GMB dengan terdapatnya kecepatan sudut yang berubah beraturan (atau adanya percepatan sudut). Langkah-langkah yang sama dapat dilakukan, akan tetapi perlu diingat bahwa

\omega \rightarrow \omega(t) = \int \alpha dt = \omega_0 + \alpha t \!

dengan $\alpha\!$ percepatan sudut dan $\omega_0\!$ kecepatan sudut mula-mula. Penurunan GMBB ini akan menjadi sedikit lebih rumit dibandingkan pada kasus GMB di atas.

Persamaan parametrik di atas, dapat dituliskan dalam bentuk yang lebih umum, yaitu:

x(t) = x_c + R \cos \theta \!

y(t) = y_c + R \sin \theta \!

di mana $\theta = \theta(t) \!$ adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara $\theta \!$ , $\omega \!$ dan $\alpha \!$ melalui proses integrasi dan diferensiasi, maka dalam kasus GMBB hubungan-hubungan tersebut mutlak diperlukan.

Kecepatan sudut

Dengan menggunakan aturan rantai dalam melakukan diferensiasi posisi dari persamaan parametrik terhadap waktu diperoleh

v_x(t) = - R \sin \theta\ \frac{d\theta}{dt} = - \omega(t) R \sin \theta \!

v_y(t) = R \cos \theta \ \frac{d\theta}{dt} = \omega(t) R \cos \theta \!

dengan

\frac{d\theta}{dt} = \omega(t) = \omega_0 + \alpha\ t \!

Dapat dibuktikan bahwa

v(t) = v_T(t) = \sqrt{v_x^2(t) + v_y^2(t)} = \omega(t) R \!

sama dengan kasus pada GMB.

Gerak berubah beraturan (melingkar)

Gerak melingkar dapat dipandang sebagai gerak berubah beraturan. Bedakan dengan gerak lurus berubah beraturan (GLBB). Konsep kecepatan yang berubah kadang hanya dipahami dalam perubahan besarnya, dalam gerak melingkar beraturan (GMB) besarnya kecepatan adalah tetap, akan tetapi arahnya yang berubah dengan beraturan, bandingkan dengan GLBB yang arahnya tetap akan tetapi besarnya kecepatan yang berubah beraturan.

Gerak berubah beraturan
Kecepatan	GLBB	GMB
Besar	berubah	tetap
Arah	tetap	berubah

Besaran Gerak Melingkar

Besaran-besaran yang mendeskripsikan suatu gerak melingkar adalah $\theta\!$ , $\omega\!$ dan $\alpha\!$ atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan $r\!$ , $v\!$ dan $a\!$ .

**Besaran gerak lurus dan melingkar**
Gerak lurus		Gerak melingkar
Besaran	Satuan (SI)	Satuan (SI)
posisi $r\!$	m	rad
kecepatan $v\!$	m/s	rad/s
percepatan $a\!$	m/s²	rad/s²
–	–	s
–	–	m

Turunan dan integral

Seperti halnya kembarannya dalam gerak linier, besaran-besaran gerak melingkar pun memiliki hubungan satu sama lain melalui proses integrasi dan diferensiasi.

\int \omega \ dt=\theta \quad \leftrightarrow \quad \omega ={\frac {d\theta }{dt}}

\int \alpha \ dt=\omega \quad \leftrightarrow \quad \alpha ={\frac {d\omega }{dt}}

\int \int \alpha \ dt^{2}=\theta \quad \leftrightarrow \quad \alpha ={\frac {d^{2}\theta }{dt^{2}}}

Hubungan antar besaran sudut dan tangensial

Antara besaran gerak linier dan melingkar terdapat suatu hubungan melalui $R\!$ khusus untuk komponen tangensial, yaitu

\theta = \frac{r_T}{R}\ \ , \ \ \omega = \frac{v_T}{R}\ \ , \ \ \alpha = \frac{a_T}{R}

Perhatikan bahwa di sini digunakan $r_T\!$ yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu

r_T \approx |\overrightarrow{r}(t+\Delta t)-\overrightarrow{r}(t)|\!

untuk suatu selang waktu kecil atau sudut yang sempit.

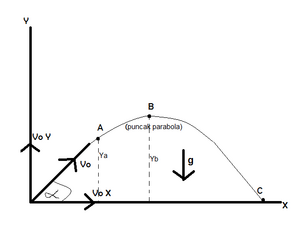
Gerak Parabola

Gerak parabola adalah gerak yang membentuk sudut tertentu terhadap bidang horizontal. Pada gerak parabola, gesekan diabaikan, dan gaya yang bekerja hanya gaya berat/percepatan gravitasi.

Pada titik awal,

$Vo_{x}=Vo\times \cos \alpha$

$Vo_{y}=Vo\times \sin \alpha$

Pada titik A (t = t_a):

$Va_{x}=Vo_{x}=Vo\times \cos \alpha$

$Va_{y}=Vo_{y}-g\times t_{a}$

Letak/posisi di A:

$X_{a}=Vo_{x}\times t_{a}$

$Y_{a}=Vo_{y}\times t_{a}-1/2g{t_{a}^{2}}$

Titik tertinggi yang bisa dicapai (B):

$h_{max}={\frac {{(Vo\times \sin \alpha })^{2}}{2g}}={\frac {{(Vo^{2}\times \sin ^{2}\alpha })}{2g}}$

Waktu untuk sampai di titik tertinggi (B) (t_b):

$V_{y}=0$

$V_{y}=Vo_{y}-gt$

$0=Vo\sin \alpha -gt$

$t_{b}={\frac {{(Vo\times \sin \alpha })}{g}}={\frac {Vo_{y}}{g}}$

Jarak mendatar/horizontal dari titik awal sampai titik B (Xb):

$X_{b}=Vo_{x}\times t_{b}$

$X_{b}=Vo\cos \alpha \times ({\frac {{(Vo\times \sin \alpha })}{g}})$

$X_{b}={\frac {{Vo^{2}}\times \sin 2\alpha }{2g}}$

Jarak vertikal dari titik awal ke titik B (Yb):

$Y_{b}={\frac {Vo_{y}^{2}}{2g}}$

$Y_{b}={\frac {{Vo^{2}}\times \sin ^{2}\alpha }{2g}}$

Waktu untuk sampai di titik C:

$t_{total}={\frac {{(2Vo\times \sin \alpha })}{g}}={\frac {2Vo_{y}}{g}}$

Jarak dari awal bola bergerak sampai titik C:

$X_{maks}=Vo{x}\times t_{total}$

$X_{maks}=Vo\times \cos \alpha \times {\frac {{(2Vo\times \sin \alpha })}{g}}$

$X_{maks}={\frac {{Vo^{2}}\times \sin 2\alpha }{g}}$

Gerak Setengah Parabola

Benda yang dilempar mendatar dari suatu ketinggian tertentu dianggap tersusun atas dua macam gerak, yaitu :

a.	*Gerak pada arah sumbu X (GLB)* v_x = v₀ S_x = X = v_x t
b.	*Gerak pada arah sumbu Y (GJB/GLBB)* v_y = 0 ]® Jatuh bebas y = 1/2 g t²

Gerak Parabola/Peluru

Benda yang dilempar ke atas dengan sudut tertentu, juga tersusun atas dua macam gerak dimanalintasan
dan kecepatan benda harus diuraikan pada arah X dan Y.

a.	*Arah sb-X (GLB)* v_0x = v₀ cos q (tetap) X = v_0xt = v₀cos q.t
b.	*Arah sb-Y (GLBB)* v_0y = v₀ sin q Y = v_oyt – 1/2 g t² = v₀sin q . t – 1/2 g t² v_y = v₀ sin q – g t

Syarat mencapai titik P (titik tertinggi): v_y = 0

t_op = v₀ sin q / g

sehingga

t_op = t_pqt_oq = 2 t_op

OQ = v_0x t_Q = V₀²sin 2q / g

h _max = v _oy t_p – 1/2 gt_p² = V₀²sin² q / 2g

vt = Ö (vx)² + (vy)²

Contoh:

1. Sebuah benda dijatuhkan dari pesawat terbang yang sedang melaju horisontal 720 km/jam dari ketinggian 490 meter. Hitunglah jarak jatuhnya benda pada arah horisontal ! (g = 9.8 m/det²).

Jawab:

v_x = 720 km/jam = 200 m/det.
h = 1/2 gt² ® 490 = 1/2 . 9.8 . t²
t = 100 = 10 detik
X = v_x. t = 200.10 = 2000 meter

2. Peluru A dan peluru B ditembakkan dari senapan yang sama dengan sudut elevasi yang berbeda; peluru A dengan 30^o dan peluru B dengan sudut 60^o. Berapakah perbandingan tinggi maksimum yang dicapai peluru A dan peluru B?

Jawab:

Peluru A:

h_A = V₀²sin² 30^o / 2g = V₀² 1/4 /2g = V₀² / 8g

Peluru B:

h_B = V₀²sin² 60^o / 2g = V₀² 3/4 /2g = 3 V₀² / 8g

h_A = h_B= V₀²/8g : 3 V₀² / 8g = 1 : 3

Contoh Soal Gerak Fisika dan Jawaban

1. Cindy mengendarai sepeda motor dengan kecepatan tetap 36 km/jam selama 10 sekon. Berapakah jarak yang ditempuh oleh Cindy?

Jawaban: t = 10 s ; v = 36 km/jam harus diubah menjadi m/s

maka v = 36000 meter : 3600 sekon = 10 m/s
S = v x t
S = 10 m/s x 10 s
S = 100 m
Jadi jarak yang telah ditempuh oleh Cindy adalah 100 meter.

2. Jarak rumah Michael ke sekolah adalah 2 km. Jika ia mengendarai sepeda dengan kecepatan 4 m/s, berapa lama (waktu) ia sampai di sekolah?

a. 0,5 sekon
b. 8 sekon
c. 500 sekon
d. 800 sekon

Jawaban: s = 2 km = 2000 meter ; v = 4 m/s
ditanya t = …
s = v x t ==> maka t = s /t
t = 2000 / 4 = 500 sekon
Jadi jawabannya C

3. Pak Toni mengayuh sepeda dengan kecepatan 2 m/s selama 20 detik. Berapakah jarak yang ditempuh Pak Toni?

jawaban: v = 2 m/s ; t = 20 s
S = V x t
S = 2 m/s x 20 s
S = 40 m
Jadi jarak yang telah ditempuh Pak Toni 40 meter.

4. Irwan mau pergi ke kota Tegal untuk membeli Hp pada pukul 05.00 pagi. Jarak rumah Yanu ke Kota Tegal adalah 150 km. Jika Irwan mengendarai sepeda motor dengan kecepatan 50 km/jam. Jam berapa Irwan sampai di Kota Tegal?

a. 06.00
b. 07.00
c. 08.00
d. 09.00

Jawaban: karena satuan di atas km dan jam, maka kita tidak perlu mengubah satuan tersebut.

Jam berangkat 05.00 ; s = 150 km ; v = 50 km/jam
ditanya waktu sampai = jam berangkat + waktu tempuh
waktu tempuh t = s/v
t = 150 / 50 = 3 jam
Waktu sampai = 05.00 + 3 jam = 08.00

5. Ada sebuah bus melaju di jalan tol yang lurus. Selama 30 menit pertama bus menempuh jarak 45 km, 15 menit berikutnya menempuh jarak 15 km, 15 menit terkhir menmpuh jarak 20 km. Berapakah kecepatan rata-rata bus tersebut?

Total jarak yang ditempuh = 45 + 15 + 20 = 80 km
Total waktu = 30 + 15 + 15 = 60 menit

v = 80 / 1 = 80 km/jam

6. Irene mengendarai sepeda dengan kecepata 4m/s. Berapakah jarak yang di tempuh mobil tersebut selama 10 sekon?

Jawaban:

Diketahui:
kecepatan (V) = 4m/s
waktu (t) = 10 s
ditanya, s=?
jarak (s) = 4 X 10 = 400 meter

7. Jarak rumah Ibu Sinta dengan kantornya 18 km. Bu Anita hanya bisa mengendarai mobilnya dengan pelan kecepatannya 36 km/jam. Sedangkan jam kantor masuknya pada pukul 07.00. Pada pukul berapa agar Ibu Sinta harus berangkat ke kantor agar tidak terlambat?

a. 06.20
b. 06.30
c. 06.40
d. 06.50

Jawaban: s = 18 km ; v = 36 km/jam ==>> karena satuannya sama=sama km dan jam maka tidak harus diubah menjadi meter dan sekon.

t = s/v
t = 18 / 36 = 1/2 jam

Jadi waktu untuk sampai di kantor 1/2 jam atau 30 menit. Pada pilihan yang paling tepat agar tidak telat ke kantor adalah A. 06.20 sehingga Ibu Sinta akan sampai pada pukul 06.50.

8. Sebuah bola dilontarkan dari atap sebuah gedung yang tingginya adalah h = 10 m dengan kelajuan awal $V_{0}$ = 10 m/s. Jika percepatan gravitasi bumi adalah 10 $m/s^{2}$ , sudut yang terbentuk antara arah lemparan bola dengan arah horizontal adalah 30 $^{o}$ (gesekan bola dengan udara diabaikan). Waktu yang diperlukan bola untuk menyentuh tanah dan jarak mendatar yang dicapai bola berturut-turut adalah…

$\textrm{A.} \; \; \; 2 \; \textrm{dan} \; 10 \sqrt{3}$
$\textrm{B.} \; \; \; 1 \; \textrm{dan} \; 10 \sqrt{3}$
$\textrm{C.} \; \; \; 2 \; \textrm{dan} \; 5 \sqrt{3}$
$\textrm{D.} \; \; \; 1 \; \textrm{dan} \; 5 \sqrt{3}$
$\textrm{E.} \; \; \; 2 \; \textrm{dan} \; 7 \sqrt{3}$

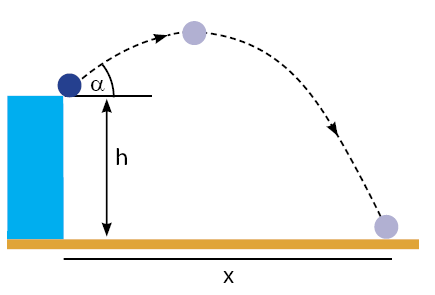
Pembahasan:

Mencari waktu yang diperlukan bola untuk menyentuh tanah ketinggian gedung h atau sama dengan y.

$y = V_{0}t \cdot sin \; \alpha - \frac{1}{2}gt^{2}$

$y = 10 \cdot t \cdot sin \; 30^{o} - \frac{1}{2} \cdot 10 \cdot t^{2}$

$-10 = 10 \cdot \frac{1}{2} \cdot t - \frac{1}{2} \cdot 10 \cdot t^{2}$

$-10 = 5t - 5t^{2}$

$5t^{2} - 5t + 10 = 0$

$t^{2} - t + 2 = 0$

$\left( t - 2\right) \left( t + 1 \right) = 0$

$t \; = \; 2 \; \textrm{atau} \; t \; = \; -1$

Sehingga waktu yang diperlukan bola untuk menyentuh tanah dari ketinggian h = 10 dari atas gedung adalah 2 sekon (ambil nilai positif).

Mencari jarak mendatar yang dicapai bola.

$x = V_{0}t \cdot cos \; t$
$x = 10 \cdot 2 \cdot cos \; 30^{o}$
$x = 10 \cdot 2 \cdot \frac{1}{2} \sqrt{3}$
$x = 10 \sqrt{3} \; \textrm{meter}$

Jadi, waktu yang diperlukan bola untuk menyentuh tanah adalah 2 sekon dan jarak yang dapat dicapai bola dalah $10 \sqrt{3}$ meter.

Jawaban: A

9. Peluru ditembakkan condong ke atas dengan kecepatan awal $V \; = \; 1,4 \times 10^{3} \; m/s$ dan mengenai sasaran yang jarak mendatarnya sejauh $2 \times 10^{5}$ m. Bila percepatan gravitasi 9,8 $m/s^{2}$ , maka besar sudut elevasinya adalah…

A.    $10^{o}$
B.    $30^{o}$
C.    $45^{o}$
D.    $60^{o}$
E.    $75^{o}$

Pembahasan:

Berdasarkan informasi pada soal dapat diperoleh informasi bahwa.

$V_{0} = 1,4 \times 10^{3} \; m/s$

$x_{max} = 2 \times 10^{5} \; m$

Besar sudut elevasi dapat diperoleh dari rumus jarak mendatar maksimum. Caranya adalah sebagai berikut.

$x_{max} = \frac{V_{0}^{2} \cdot sin \; 2 \alpha}{g}$

$2 \times 10^{5} = \frac{ \left( 1,4 \times 10^{3} \right)^{2} \cdot sin \; 2 \alpha}{9,8}$

$sin \; 2 \alpha = \frac{ 2 \times 10^{5} \times 9,8}{ \left( 1,4 \times 10^{3} \right)^{2} }$

$sin \; 2 \alpha = \frac{ 19, 6 \times 10^{5} }{ \left( 1,96 \times 10^{6} \right) }$

$sin \; 2 \alpha = \frac{ 19, 6 \times 10^{5} }{ \left( 19,6 \times 10^{5} \right) }$

$sin \; 2 \alpha = 1$

$sin \; 2 \alpha = sin \; 90^{o}$

$2 \alpha = 90^{o}$

$\alpha = \frac{90^{o}}{2} = 45^{o}$

Jawaban: C

10. Sebuah roda dengan radius 48 cm diputar melingkar beraturan dengan kelanjuan linear 1,2 m/s. Maka kecepatan sudutnya adalah…

Pembahasan dan jawaban:

Diketahui

r = 48 cm = 0,48
v = 1,2 m/s

Ditanya :

ω ?

Jawaban:

ω = v/r
= 1,2 / 0,4
= 2,5 rad/s

11. Sebuah roda melakukan gerakan melingkar sebanyak 7200 kali per menit. Maka kecepatan sudut roda tersebut adalah…

Pembahasan

Diketahui:

f = 7200 / menit = 7200 / 60 detik = 30 putaran / s = 30 Hz

Ditanya :
ω ?

Jawab :

ω = 2πf
= 2π x 3
= 60 rad/s

12. Sebuah benda melakukan gerakan melingkar dengan kecepatan sudut konstan 0,5π rad/s. Berapa putaran yang dapat dilakukan benda tersebut dalam satu menit ?

Pembahasan

Diketahui:

ω = 0,5π rad/s

Ditanya :
f ?

Jawab :

ω = 2πf
f = ω/2π
= 0,5π / 2π
= 4 Hz

Bacaan Lainnya

Sumber bacaan: Physics, Tutor Vista

Rumus Gerak Fisika – Gerak Lurus Beraturan, Gerak Lurus Berubah Beraturan, Melingkar, Parabola – Beserta Soal dan Jawaban

Rumus Gerak Fisika

Gerak lurus beraturan

Rumus gerak lurus beraturan:

Kecepatan rata-rata

Gerak Lurus Berubah Beraturan

Gerak vertikal ke atas

Gerak jatuh bebas

Gerak vertikal ke bawah

Gerak Melingkar atau Gaya Sentripetal

Perpindahan sudut, kecepatan sudut dan percepatan sudut

Percepatan sentripetal

Gerak melingkar beraturan

Gerak melingkar berubah beraturan

Persamaan Parametrik (gerak melingkar)

Hubungan antar besaran linier dan angular

Kecepatan tangensial dan kecepatan sudut

Percepatan tangensial dan kecepatan sudut

Kecepatan sudut tidak tetap

Kecepatan sudut

Gerak berubah beraturan (melingkar)

Besaran Gerak Melingkar

Turunan dan integral

Hubungan antar besaran sudut dan tangensial

Gerak Parabola

Gerak Setengah Parabola

Gerak Parabola/Peluru

Syarat mencapai titik P (titik tertinggi): vy = 0

Contoh Soal Gerak Fisika dan Jawaban

1. Cindy mengendarai sepeda motor dengan kecepatan tetap 36 km/jam selama 10 sekon. Berapakah jarak yang ditempuh oleh Cindy?

2. Jarak rumah Michael ke sekolah adalah 2 km. Jika ia mengendarai sepeda dengan kecepatan 4 m/s, berapa lama (waktu) ia sampai di sekolah?

3. Pak Toni mengayuh sepeda dengan kecepatan 2 m/s selama 20 detik. Berapakah jarak yang ditempuh Pak Toni?

4. Irwan mau pergi ke kota Tegal untuk membeli Hp pada pukul 05.00 pagi. Jarak rumah Yanu ke Kota Tegal adalah 150 km. Jika Irwan mengendarai sepeda motor dengan kecepatan 50 km/jam. Jam berapa Irwan sampai di Kota Tegal?

5. Ada sebuah bus melaju di jalan tol yang lurus. Selama 30 menit pertama bus menempuh jarak 45 km, 15 menit berikutnya menempuh jarak 15 km, 15 menit terkhir menmpuh jarak 20 km. Berapakah kecepatan rata-rata bus tersebut?

6. Irene mengendarai sepeda dengan kecepata 4m/s. Berapakah jarak yang di tempuh mobil tersebut selama 10 sekon?

7. Jarak rumah Ibu Sinta dengan kantornya 18 km. Bu Anita hanya bisa mengendarai mobilnya dengan pelan kecepatannya 36 km/jam. Sedangkan jam kantor masuknya pada pukul 07.00. Pada pukul berapa agar Ibu Sinta harus berangkat ke kantor agar tidak terlambat?

10. Sebuah roda dengan radius 48 cm diputar melingkar beraturan dengan kelanjuan linear 1,2 m/s. Maka kecepatan sudutnya adalah…

11. Sebuah roda melakukan gerakan melingkar sebanyak 7200 kali per menit. Maka kecepatan sudut roda tersebut adalah…

12. Sebuah benda melakukan gerakan melingkar dengan kecepatan sudut konstan 0,5π rad/s. Berapa putaran yang dapat dilakukan benda tersebut dalam satu menit ?

Bacaan Lainnya

Nilai Pi 1 juta digit pertama | Analisis dan…

Menghitung Dimensi Balok dari Luas Jaring-Jaringnya

Rahasia Kehidupan Harimau: Mengenal Lebih Dekat dengan Sang Raja…

Tinggalkan Balasan Batalkan balasan

Syarat mencapai titik P (titik tertinggi): v_y = 0