Pengertian Gaya Sentripetal atau Gerak Melingkar

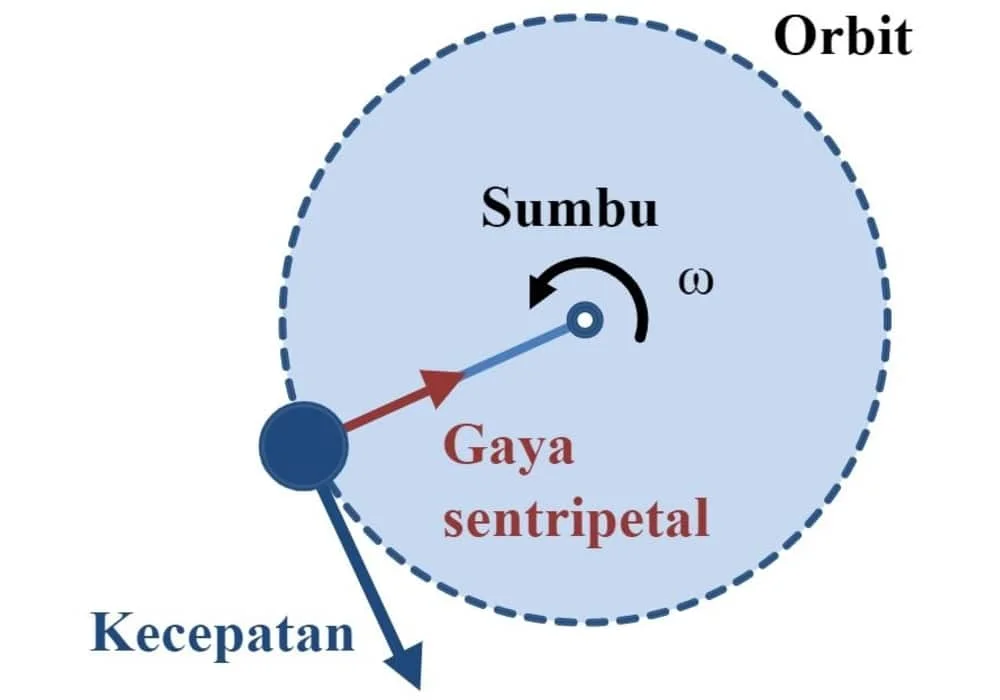
Gaya sentripetal adalah gaya yang membuat benda untuk bergerak melingkar. Gaya ini bukan merupakan gaya fisis, atau gaya dalam arti sebenarnya, melainkan hanya suatu penamaan atau penggolongan jenis-jenis gaya yang berfungsi membuat benda bergerak melingkar.

Bermacam-macam gaya fisis dapat digunakan sebagai gaya sentripetal, antara lain gaya gravitasi, elektrostatik, tegangan tali, gesekan dan lainnya. Istilah sentripetal berasal dari kata bahasa Latin, yaitu centrum (“pusat”) dan petere(“menuju arah”), yang berarti menuju arah pusat lingkaran.

Kenapa gaya sentripetal bukan merupakan gaya fisis?

Yang dimaksud gaya sentripetal bukan merupakan gaya fisis atau gaya dalam arti yang sebenarnya adalah karena gaya sentripetal hanyalah suatu sebutan untuk jenis-jenis gaya yang berfungsi membuat benda bergerak melingkar.

Contoh Gaya Sentripetal

Gerak bulan dan satelit buatan yang mengelilingi bumi.

Gerak planet mengelilingi matahari.

Gesekan antara ban kendaraan dengan jalan saat berbelok di tikungan melengkung.

Gerak benda yang diputar baik vertikal maupun horizontal dengan menggunakan seutas tali.
Gerak Roller Coaster saat melewati lintasan melingkar.

Rumus Gaya Sentripetal

Gaya sentripetal memiliki besar sebanding kuadrat kecepatan tangensial benda dan berbanding terbalik dengan jari-jari lintasan

\!F_{s}=m{\frac {v^{2}}{r}}

dengan arah menuju pusat lintasan berbentuk lingkaran, yang menunjukkan bahwa terdapat suatu percepatan sentripetal, yaitu

\!a_{s}={\frac {v^{2}}{r}}

apabila dianalogikan dengan hukum kedua Newton.

\!F=ma

Representasi vektor

Dalam notasi vektor dengan sistem koordinat polar, gaya sentripetal dapat dituliskan sebagai

\!{\vec {F_{s}}}=-m{\frac {v^{2}}{r}}{\hat {r}}

Vektor-vektor sesaat gaya sentripetal.

dengan

\!{\hat {r}}={\frac {\vec {r}}{r}}

adalah vektor satuan dalam arah radial, yang umumnya dipilih bernilai positif mengarah ke luar lingkaran.

Representasi produk perkalian vektor

Atau dapat pula dituliskan sebagai produk dari perkalian vektor.

{\vec {F}}_{s}=-{\frac {mv^{2}}{r}}{\hat {r}}=-{\frac {mv^{2}}{r}}{\frac {\vec {r}}{r}}=-m\omega ^{2}{\vec {r}}=m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})

Dengan arah ${\vec {\omega }}$ mengikuti aturan tangan kanan. Dalam kasus seperti ditunjukkan dalam gambar, besaran-besaran vektor yang dimaksud bernilai:

\!{\vec {\omega }}=\omega \ {\hat {k}}

\!{\vec {r}}=r\left[\cos(\omega t)\ {\hat {i}}+\sin(\omega t)\ {\hat {j}}\right]

dan sebagai konsekuensinya

\!{\hat {r}}=\cos(\omega t)\ {\hat {i}}+\sin(\omega t)\ {\hat {j}}

\!{\vec {v}}={\vec {\omega }}\times {\vec {r}}=\omega r\ \left[-\sin(\omega t)\ {\hat {i}}+\cos(\omega t)\ {\hat {j}}\right]

Dengan demikian dapat dibuktikan bahwa

{\vec {F}}_{s}=m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})=m{\vec {\omega }}\times {\vec {v}}

=m(\omega {\hat {k}})\times \left(\omega r\ \left[-\sin(\omega t)\ {\hat {i}}+\cos(\omega t)\ {\hat {j}}\right]\right)

=m\omega ^{2}r\left[-\sin(\omega t)\ {\hat {j}}-\cos(\omega t)\ {\hat {i}}\right]

=m\omega ^{2}r\left\{-\left[\sin(\omega t)\ {\hat {j}}+\cos(\omega t)\ {\hat {i}}\right]\right\}

=m\omega ^{2}r(-{\hat {r}})=-m\omega ^{2}{\vec {r}}

seperti dituliskan sebelumnya, yang menunjukkan bahwa gaya sentripetal selalu menuju ke pusat lintasan lingkaran.

Besaran gerak melingkar

Besaran-besaran yang mendeskripsikan suatu gerak melingkar adalah $\theta\!$ , $\omega\!$ dan $\alpha\!$ atau berturur-turut berarti sudut, kecepatan sudut dan percepatan sudut. Besaran-besaran ini bila dianalogikan dengan gerak linier setara dengan posisi, kecepatan dan percepatan atau dilambangkan berturut-turut dengan $r\!$ , $v\!$ dan $a\!$ .

**Besaran gerak lurus dan melingkar**
Gerak lurus		Gerak melingkar
Besaran	Satuan (SI)	Besaran	Satuan (SI)
poisisi $r\!$	m	sudu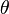t $\theta\!$ theta	rad
kecepatan 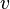$v\!$	m/s	kecepatan sudut $\omega\!$ omega	rad/s
percepatan $a\!$	m/s²	percepatan sudut $\alpha\!$ alpha	rad/s²
–	–	perioda 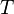$T\!$	s
–	–	radius $R\!$	m

Turunan dan integral

Seperti halnya kembarannya dalam gerak linier, besaran-besaran gerak melingkar pun memiliki hubungan satu sama lain melalui proses integrasi dan diferensiasi.

\int \omega \ dt=\theta \quad \leftrightarrow \quad \omega ={\frac {d\theta }{dt}}

\int \alpha \ dt=\omega \quad \leftrightarrow \quad \alpha ={\frac {d\omega }{dt}}

\int \int \alpha \ dt^{2}=\theta \quad \leftrightarrow \quad \alpha ={\frac {d^{2}\theta }{dt^{2}}}

Hubungan antar besaran sudut dan tangensial

Antara besaran gerak linier dan melingkar terdapat suatu hubungan melalui $R\!$ khusus untuk komponen tangensial, yaitu:

\theta = \frac{r_T}{R}\ \ , \ \ \omega = \frac{v_T}{R}\ \ , \ \ \alpha = \frac{a_T}{R}

Perhatikan bahwa di sini digunakan $r_T\!$ yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu:

r_T \approx |\overrightarrow{r}(t+\Delta t)-\overrightarrow{r}(t)|\!

untuk suatu selang waktu kecil atau sudut yang sempit.

Jenis Gerak Melingkar atau Gaya Sentripetal

Gerak melingkar dapat dibedakan menjadi dua jenis, atas keseragaman kecepatan sudutnya $\omega\!$ , yaitu:

Gerak melingkar beraturan.
Gerak melingkar berubah beraturan.

Gerak melingkar beraturan

Gerak Melingkar Beraturan (GMB) adalah gerak melingkar dengan besar kecepatan sudut $\omega\!$ tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial $v_T\!$ dengan jari-jari lintasan $R\!$ .

\omega = \frac {v_T} R

Arah kecepatan linier $v\!$ dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial $v_T\!$ . Tetapnya nilai kecepatan $v_T\!$ akibat konsekuensi dar tetapnya nilai $\omega\!$ . Selain itu terdapat pula percepatan radial $a_R\!$ yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.

a_R = \frac {v^2} R = \frac {v_T^2} R

Bila $T\!$ adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran $\theta = 2\pi R\!$ , maka dapat pula dituliskan

v_T = \frac {2\pi R} T \!

Kinematika gerak melingkar beraturan adalah

\theta(t) = \theta_0 + \omega\ t

dengan $\theta(t)\!$ adalah sudut yang dilalui pada suatu saat $t\!$ , $\theta_0\!$ adalah sudut mula-mula dan $\omega\!$ adalah kecepatan sudut (yang tetap nilainya).

Gerak melingkar berubah beraturan

Gerak Melingkar Berubah Beraturan (GMBB) adalah gerak melingkar dengan percepatan sudut $\alpha\!$ tetap. Dalam gerak ini terdapat percepatan tangensial $a_T\!$ (yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial $v_T\!$ ).

\alpha = \frac {a_T} R

Kinematika GMBB adalah

\omega(t) = \omega_0 + \alpha\ t \!

\theta(t) = \theta_0 + \omega_0\ t + \frac12 \alpha\ t^2 \!

\omega^2(t) = \omega_0^2 + 2 \alpha\ (\theta(t) - \theta_0) \!

dengan $\alpha\!$ adalah percepatan sudut yang bernilai tetap dan $\omega_0\!$ adalah kecepatan sudut mula-mula.

Persamaan Parametrik

Gerak melingkar dapat pula dinyatakan dalam persamaan parametrik dengan terlebih dahulu mendefinisikan:

titik awal gerakan dilakukan $(x_0,y_0)\!$
kecepatan sudut putaran $\omega\!$ (yang berarti suatu GMB)
pusat lingkaran $(x_c,y_c)\!$

untuk kemudian dibuat persamaannya.

Hal pertama yang harus dilakukan adalah menghitung jari-jari lintasan $R\!$ yang diperoleh melalui:

R = \sqrt{(x_0 - x_c)^2 + (y_0 - y_c)^2} \!

Setelah diperoleh nilai jari-jari lintasan, persamaan dapat segera dituliskan, yaitu

x(t)=x_{c}+R\cos(\omega t+\phi _{x})\!

y(t)=y_{c}+R\sin(\omega t+\phi _{y})\!

dengan dua konstanta $\phi_x \!$ dan $\phi_y \!$ yang masih harus ditentukan nilainya. Dengan persyaratan sebelumnya, yaitu diketahuinya nilai $(x_0,y_0)\!$ , maka dapat ditentukan nilai $\phi_x \!$ dan $\phi_y \!$ :

\phi_x = \arccos \left( \frac{x_0 - x_c}{R} \right)\!

\phi_y = \arcsin \left( \frac{y_0 - y_c}{R} \right)\!

Perlu diketahui bahwa sebenarnya

\phi_x = \phi_y \!

karena merupakan sudut awal gerak melingkar.

Hubungan antar besaran linier dan angular

Dengan menggunakan persamaan parametrik, telah dibatasi bahwa besaran linier yang digunakan hanyalah besaran tangensial atau hanya komponen vektor pada arah angular, yang berarti tidak ada komponen vektor dalam arah radial.

Dengan batasan ini hubungan antara besaran linier (tangensial) dan angular dapat dengan mudah diturunkan.

Kecepatan tangensial dan kecepatan sudut

Kecepatan linier total dapat diperoleh melalui

v = \sqrt{v_x^2 + v_y^2}

dan karena batasan implementasi persamaan parametrik pada gerak melingkar, maka

v_T = v = \sqrt{v_x^2 + v_y^2}

dengan

v_x = \dot{x} = \frac{dx}{dt}

v_y = \dot{y} = \frac{dy}{dt}

diperoleh

v_x = -\omega R \sin(\omega t + \phi_x) \!

v_y = \omega R \cos(\omega t + \phi_x) \!

sehingga

v_T = \sqrt{(-\omega)^2 R^2 \sin^2(\omega t + \phi_x) + \omega^2 R^2 \cos^2(\omega t + \phi_x)}\!

v_T = \omega R \sqrt{\sin^2(\omega t + \phi_x) + \cos^2(\omega t + \phi_x)}\!

v_T = \omega R\!

Percepatan tangensial dan kecepatan sudut

Dengan cara yang sama dengan sebelumnya, percepatan linier total dapat diperoleh melalui

a = \sqrt{a_x^2 + a_y^2}

dan karena batasan implementasi persamaan parametrik pada gerak melingkar, maka

a_T = a = \sqrt{a_x^2 + a_y^2}

dengan

a_x = \ddot{x} = \frac{d^2x}{dt^2}

a_y = \ddot{y} = \frac{d^2y}{dt^2}

diperoleh

a_x = -\omega^2 R \cos(\omega t + \phi_x) \!

a_y = -\omega^2 R \sin(\omega t + \phi_x) \!

sehingga

a_T = \sqrt{(-\omega)^4 R^2 \cos^2(\omega t + \phi_x) + \omega^4 R^2 \sin^2(\omega t + \phi_x)}\!

a_T = \omega^2 R \sqrt{\cos^2(\omega t + \phi_x) + \sin^2(\omega t + \phi_x)}\!

a_T = \omega^2 R\!

Kecepatan sudut tidak tetap

Persamaan parametric dapat pula digunakan apabila gerak melingkar merupakan GMBB, atau bukan lagi GMB dengan terdapatnya kecepatan sudut yang berubah beraturan (atau adanya percepatan sudut). Langkah-langkah yang sama dapat dilakukan, akan tetapi perlu diingat bahwa

\omega \rightarrow \omega(t) = \int \alpha dt = \omega_0 + \alpha t \!

dengan $\alpha\!$ percepatan sudut dan $\omega_0\!$ kecepatan sudut mula-mula. Penurunan GMBB ini akan menjadi sedikit lebih rumit dibandingkan pada kasus GMB di atas.

Persamaan parametrik di atas, dapat dituliskan dalam bentuk yang lebih umum, yaitu:

x(t) = x_c + R \cos \theta \!

y(t) = y_c + R \sin \theta \!

di mana $\theta = \theta(t) \!$ adalah sudut yang dilampaui dalam suatu kurun waktu. Seperti telah disebutkan di atas mengenai hubungan antara $\theta \!$ , $\omega \!$ dan $\alpha \!$ melalui proses integrasi dan diferensiasi, maka dalam kasus GMBB hubungan-hubungan tersebut mutlak diperlukan.

Kecepatan sudut

Dengan menggunakan aturan rantai dalam melakukan diferensiasi posisi dari persamaan parametrik terhadap waktu diperoleh

v_x(t) = - R \sin \theta\ \frac{d\theta}{dt} = - \omega(t) R \sin \theta \!

v_y(t) = R \cos \theta \ \frac{d\theta}{dt} = \omega(t) R \cos \theta \!

dengan

\frac{d\theta}{dt} = \omega(t) = \omega_0 + \alpha\ t \!

Dapat dibuktikan bahwa

v(t) = v_T(t) = \sqrt{v_x^2(t) + v_y^2(t)} = \omega(t) R \!

sama dengan kasus pada GMB.

Gerak Berubah Beraturan

Gerak melingkar dapat dipandang sebagai gerak berubah beraturan. Bedakan dengan gerak lurus berubah beraturan (GLBB).

Konsep kecepatan yang berubah kadang hanya dipahami dalam perubahan besarnya, dalam gerak melingkar beraturan (GMB) besarnya kecepatan adalah tetap, akan tetapi arahnya yang berubah dengan beraturan, bandingkan dengan GLBB yang arahnya tetap akan tetapi besarnya kecepatan yang berubah beraturan.

**Gerak berubah beraturan**
Kecepatan	GLBB	GMB
Besar	berubah	tetap
Arah	tetap	berubah

Contoh Soal dan Jawaban Sentripetal

1. Sebuah benda bergerak dengan kelajuan tetap $v$ melalui lingkaran berjari-jari $r$ dengan percepatan sentripetal $a_{s}$ .
a) Agar percepatan sentripetalnya menjadi dua kali semula, maka?
b) Apabila $v$ dijadikan 4 kali semula dan $r$ dijadikan 2 kali semula, maka a_s menjadi?

a) Gunakan hukum kesebandingan
Mari kita tinjau dari hubungan pertama:
$a_{s} = ω^{2} r$

Sehingga

a_s $\alpha\!$ v² dan a_s $\alpha\!$ 1/r

Agar a_s menjadi dua kali semula, maka $r$ dapat dijadikan dua kali semula dengan menahan $ω$ tetap, atau $ω$ dijadikan $\sqrt{2}$ kali semula dengan menahan $r$ tetap.

Mari kita tinjau dari hubungan kedua:

a_s=v²/r

Sehingga

a_s $\alpha\!$ v² dan a_s $\alpha\!$ 1/r

Agar a_s menjadi dua kali semula, maka $r$ dapat dijadikan setengah kali semula dengan menahan $v$ tetap, atau $v$ dijadikan $\sqrt{2}$ kali semula dengan menahan $r$ tetap.

b) Gunakan hubungan kedua

( 4²/₂ ) = 8

maka $a_{s}$ menjadi 8 kali semula.

2. Sebuah benda bermassa 1 kg berputar dengan kecepatan sudut 120 rpm. Jika jari-jari putaran benda adalah 2 meter tentukan percepatan sentripetal gerak benda tersebut !

Pembahasan dan jawaban:
Data:
ω = 120 rpm = 4π rad/s
r = 2 meter
m = 1 kg
a_sp = …?

a_sp = ^V2/_r = ω² r
a_sp = (4π)² (2) = 32π² m/s²

3. Gaya sentripetal yang bekerja pada sebuah benda bermassa 1 kg yang sedang bergerak melingkar beraturan dengan jari-jari lintasan sebesar 2 m dan kecepatan 3 m/s adalah….?

Pembahasan dan jawaban:

Data:
m = 1 kg
r = 2 meter
V = 3 m/s
F_sp = ….?

F_sp = m ( ^V2/_r )
F_sp = (1)( ³²/₂ ) = 4,5 N

4. Nyatakan dalam satuan radian :
a) 90^o
b) 270^o

Pembahasan dan jawaban:
360^o = 2π radian

a) 90^o

$\100dpi 90^o=90^o\times \frac{2\pi\,\,radian}{360^o}=\frac{\pi}{2}\,\,rad$

b) 270^o

$\100dpi 270^o=270^o\times \frac{2\pi\,\,radian}{360^o}=\frac{3\pi}{2}\,\,rad$

5. Sebuah benda bergeak melingkar dengan kecepatan sudut 50π rad/s. Tentukan frekuensi putaran gerak benda!

Pembahasan dan jawaban:
$\100dpi \\\omega =2\pi f\\ 50\pi =2\pi f\\ f=25\,\,Hz$

6. Gaya sentripetal yang bekerja pada sebuah benda bermassa 1 kg yang sedang bergerak melingkar beraturan dengan jari-jari lintasan sebesar 2 m dan kecepatan 3 m/s adalah….?

Pembahasan dan jawaban:
Data:
m = 1 kg
r = 2 meter
V = 3 m/s
F_sp = ….?

F_sp = m ( ^V2/_r )
F_sp = (1)( ³²/₂ ) = 4,5 N

7. Kecepatan sudut sebuah benda yang bergerak melingkar adalah 12 rad/s. Jika jari-jari putarannya adalah 2 meter, tentukan besar kecepatan benda tersebut!

Pembahasan dan jawaban:
$\100dpi \\V =\omega r\\ V=(12)(2)=24\,\,m/s$

8. Dua buah roda berputar dihubungkan seperti gambar berikut!

Jika jari jari roda pertama adalah 20 cm, jari-jari roda kedua adalah 10 cm dan kecepatan sudut roda pertama adalah 50 rad/s, tentukan kecepatan sudut roda kedua!

Pembahasan dan jawaban:
Data:
r₁ = 20 cm
r₂ = 10 cm
ω₁ = 50 rad/s
ω₂ = …?

Dua roda dengan hubungan seperti soal diatas akan memiliki kecepatan (v) yang sama :

$\100dpi \\v_1=v_2\\ \omega _1r_1=\omega _2r_2\\ (50)(20)=\omega_2(10)\\ \omega_2 = 100\,\,rad/s$

9. Sebuah partikel bergerak melingkar dengan kecepatan sudut sebesar 4 rad/s selama 5 sekon. Tentukan besar sudut yang ditempuh partikel tersebut!

Pembahasan dan jawaban:
Soal di atas tentang Gerak Melingkar Beraturan. Untuk mencari sudut tempuh gunakan rumus :
θ = ωt
θ = (4)(5) = 20 radian.

10. Sebuah titik pada tepi silinder bergerak melingkar dengan kelajuan konstan 10 m/s. Jari-jari silinder = 1 meter. Tentukan (a) kelajuan tepi silinder 5 sekon kemudian (b) jarak yang ditempuh tepi silinder 5 sekon kemudian (c) percepatan sentripetal titik yang berjarak 0,5 meter dan 1 meter dari poros alias sumbu putar.

Pembahasan dan jawaban:

(a) kelajuan titik pada tepi silinder setelah 5 sekon
Silinder bergerak melingkar dengan kelajuan konstan karenanya 5 sekon kemudian, kelajuan tepi silinder tetap 10 meter/sekon

(b) jarak tempuh titik pada tepi silinder setelah 5 sekon
Tanpa rumus
Kelajuan 10 meter/sekon artinya setiap 1 sekon, titik pada tepi selinder bergerak sejauh 10 meter. Setelah 1 sekon, titik pada tepi silinder bergerak sejauh 10 meter. Setelah 2 sekon, titik pada tepi silinder bergerak sejauh 20 meter. Setelah 5 sekon, titik pada tepi silinder bergerak melingkar sejauh 50 meter.
Menggunakan rumus :
v = s / t
s = v t = (10)(5) = 50 meter
(c) percepatan sentripetal (a_s)
Percepatan sentripetal sebuah titik berjarak 0,5 meter dari poros adalah :
a_s = v² / r = 10² / 0,5 = 100 / 0,5 = 200 m/s²
Percepatan sentripetal sebuah titik berjarak 1 meter dari poros adalah :
a_s = v² / r = 10² / 0,5 = 100 / 1 = 100 m/s²

11. Dua buah roda berputar dihubungkan seperti gambar berikut!

Jika kecepatan roda pertama adalah 20 m/s jari-jari roda pertama dan kedua masing-masing 20 cm dan 10 cm, tentukan kecepatan roda kedua!

Pembahasan dan jawaban:
Kecepatan sudut untuk hubungan dua roda seperti soal adalah sama:

$\100dpi \\\omega_1=\omega_2\\ \frac{v_1}{r_1}=\frac{v_2}{r_2}\\ \frac{20}{20}=\frac{v_2}{10}\\ v_2 = 10\,\,m/s$

12. Roda sebuah mobil selalu melakukan 120 putaran setiap 60 sekon. Berapa kelajuan sudut roda ? Nyatakan dalam:
(a) revolution per minute (rpm) atau putaran per menit
(b) derajat per sekon (^o/s)
(c) radian per sekon (rad/s)

Pembahasan dan jawaban:
(a) kelajuan sudut roda dalam satuan putaran / menit (rpm)
120 putaran / 60 sekon = 120 putaran / 1 menit = 120 putaran / menit = 120 rpm

(b) kelajuan sudut roda dalam satuan derajat / sekon (^o/s)
1 putaran = 360^o, 120 putaran = 43200^o
Jadi 120 putaran / 60 sekon = (120)(360^o) / 60 sekon = 43200^o / 60 sekon = 720^o/sekon

(c) kelajuan sudut roda dalam satuan radian/sekon (rad/s)
1 putaran = 6,28 radian
Jadi 120 putaran / 60 sekon = (120)(6,28) radian / 60 sekon = 753,6 radian / 60 sekon = 12,56 radian/sekon

13. Tiga buah roda berputar dihubungkan seperti gambar berikut!

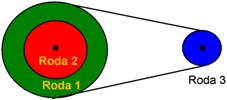
Data ketiga roda :
r₁ = 20 cm
r₂ = 10 cm
r₃ = 5 cm
Jika kecepatan sudut roda pertama adalah 100 rad/s, tentukan kecepatan sudut roda ketiga!

Pembahasan dan jawaban:
$\100dpi \\\omega_1=\omega_2=100\,\,rad/s\\ v_1=v_3\\ \omega_1r_1=\omega_3r_3\\ (100)(20)=\omega_3(5)\\ \omega_3=400\,\,rad/s$

14. Sebuah benda bergerak melingkar dengan percepatan sudut 2 rad/s². Jika mula-mula benda diam, tentukan :
a) Kecepatan sudut benda setelah 5 sekon
b) Sudut tempuh setelah 5 sekon

Pembahasan dan jawaban:
Data:
α = 2 rad/s²
ω_o = 0
t = 5 sekon
Soal tentang Gerak Melingkar Berubah Beraturan

a) ω_t = ω_o + αt
ω_t = (0) + (2)(5) = 10 rad/s

b) θ = ω_ot + ¹/₂ αt²
θ = (0)(5) + ¹/₂ (2)(5)²

15. Konversikan ke dalam satuan rad/s :
a) 120 rpm
b) 60 rpm

Pembahasan dan jawaban:
1 rpm = 1 putaran per menit
1 putaran adalah 2π radian atau
1 putaran adalah 360^o
1 menit adalah 60 sekon
a) 120 rpm

$\100dpi 120\,\,rpm=120\times\frac{1\,\,putaran}{1\,\,menit}=120\times \frac{2\pi rad} {60\,\,s}\,\,=4\pi\,\, rad/s\\$

b) 60 rpm

$\100dpi 60\,\,rpm=60\times\frac{1\,\,putaran}{1\,\,menit}=60\times \frac{2\pi\,\, rad}{60\,\,s}\,\,=2 \pi\,\, rad/s\\$

16. Sebuah bola diikat pada seutas tali yang panjangnya 2 meter lalu diputar melingkar horisontal hingga bola bergerak dengan kecepatan sudut konstan 10 radian/sekon. Tentukan besar kecepatan tangensial sebuah titik yang:
(a) berjarak 0,5 meter dari poros
(b) berjarak 1 meter dari poros
(c) berada pada tepi roda

Pembahasan dan jawaban:
Diketahui:
Panjang tali = jari-jari lintasan melingkar (r) = 2 meter
Kelajuan sudut = 10 radian/sekon
Ditanya : kelajuan tangensial sebuah titik pada (a) r = 0,5 meter (b) r = 1 meter (c) r = 2 meter
Jawaban:
Rumus hubungan antara kelajuan tangensial dan kelajuan sudut :

v = r ω
Keterangan: v = kelajuan, r = jari-jari, ω = kelajuan sudut

(a) Kelajuan tangensial (v) sebuah titik pada r = 0,5 meter
v = (0,5 meter)(10 rad/s) = 5 meter/sekon

(b) Kelajuan tangensial (v) sebuah titik pada r = 1 meter
v = (1 meter)(10 rad/s) = 10 meter/sekon

17. Jika kelajuan sudut roda berjari-jari 20 cm adalah 120 rpm, berapa jarak tempuh mobil ketika bergerak selama 10 sekon?

Pembahasan dan jawaban:
Diketahui:
Jari-jari roda (r) = 20 cm = 0,2 meter
Kelajuan sudut roda = 120 putaran / 60 sekon = 2 putaran / sekon = (2)(6,28) radian / sekon = 12,56 radian / sekon
Ditanya : jarak tempuh mobil selama 10 sekon.
Jawaban:
Kelajuan tepi roda:

v = r ω (0,2 meter) (12,56 radian/sekon) = 2,5 meter/sekon

Kelajuan tepi roda 2,5 meter / sekon artinya sebuah titik pada tepi roda bergerak sejauh 2,5 meter setiap 1 sekon. Setelah 10 sekon, titik pada tepi roda bergerak sejauh 25 meter.
Jadi jarak tempuh mobil selama 10 sekon adalah 25 meter.

18. Sebuah benda memiliki massa 100 g bergerak melingkar beraturan dengan kelajuan 3 m.s⁻¹. Jika jari-jari lintasan benda adalah 40 cm maka gaya sentripetal yang dialami benda tersebut sebesar….
A. 1,25 N B. 2,25 N C. 3,25 N D. 4,25 N E. 5,25 N

Pembahasan dan jawaban:
Massa benda, m = 100 gram = 0,1 kg, panjang tali jadi jari-jari R = 40 cm = 0,4 m dan kecepatan lienar v = 3 m/s². Maka gaya sentripetalnya adalah
F_sp = mv²/R
F_sp = (0,1 kg)(3 m/s²)²/(0,4 m) = 2,25 N

19. Sebuah bergerak dengan kelajuan konstan v melalui lintasan yang berbentuk lingkaran dengan percepatan sentripetal (a_s). Agar percepatan sentripetal menjadi 3 kali dari semula maka….
A. V dijadikan 3 kali dan R dijadikan 2 kali semula
B. V dijadikan 3 kali dan R dijadikan 4 kali semula
C. V dijadikan 2 kali dan R dijadikan 3 kali semula
D. V tetap dan R dijadikan 1/3 kali semula
E. V dijadikan 1/3 kali semula dan R tetap

Pembahasan dan jawaban:
Percepatan sentripetal a_s = ν² / R, agar percepatan sentripetal menjadi tiga kali semula, maka
Jika v dijadikan 3 kali dan R dijadikan 3 kali semula dan jila v tetap maka R dijadikan 1/3 kalinya.

20. Sebuah benda yang massanya 10 kg bergerak melingkar beraturan dengan kecepatan 4 m.s^-1. Jika jari-jari lingkaran 0,5 meter, maka:
(1) Frekuensi putarannya 4/π Hz
(2) Percepatan sentripetalnya 32 m.s^-2
(3) Gaya sentripetalnya 320 N
(4) Periodenya 4π s
Pernyataan yang benar adalah….
A. (1), (2), (3), dan (4)
B. (1), (2), dan (3)
C. (1), dan (3) saja
D. (2), dan (4) saja
E. (3), dan (4) saja

Pembahasan dan jawaban:
Massa benda, m = 10 kg, kecepatan benda, v = 4 m/s dan R = 0,5 m.
Dengan menggunakan hubungan v = ωr dan ω = 2πf, kita peroleh
f = v/(2πr) = (4 m/s)/(2π x 0,5 m) = 4/π Hz
Percepatan sentripetal benda adalah
a_s = v²/R = (4 m/s)²/(0,5 m) = 32 m/s²
gaya sentripetal diperoleh dari
F_s = ma_s = 10 kg x 32 m/s² = 320 N
Periodenya adalah
T = 1/f = π/4

Rumus Fisika Lainnya

Fisika banyak diisi dengan persamaan dan rumus fisika yang berhubungan dengan gerakan sudut, mesin Carnot, cairan, gaya, momen inersia, gerak linier, gerak harmonik sederhana, termodinamika dan kerja dan energi. Klik disini untuk melihat rumus fisika lainnya (akan membuka layar baru, tanpa meninggalkan layar ini).

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber: S-cool, Physics

Rumus Gaya Sentripetal – Gerak Melingkar – Contoh Soal dan Jawaban (Representasi dan Produk Perkalian Vektor)

Pengertian Gaya Sentripetal atau Gerak Melingkar

Kenapa gaya sentripetal bukan merupakan gaya fisis?

Contoh Gaya Sentripetal

Gerak bulan dan satelit buatan yang mengelilingi bumi.

Gerak planet mengelilingi matahari.

Gesekan antara ban kendaraan dengan jalan saat berbelok di tikungan melengkung.

Gerak benda yang diputar baik vertikal maupun horizontal dengan menggunakan seutas tali.

Gerak Roller Coaster saat melewati lintasan melingkar.

Rumus Gaya Sentripetal

Representasi vektor

Representasi produk perkalian vektor

Besaran gerak melingkar

Turunan dan integral

Hubungan antar besaran sudut dan tangensial

Jenis Gerak Melingkar atau Gaya Sentripetal

Gerak melingkar beraturan

Gerak melingkar berubah beraturan

Persamaan Parametrik

Hubungan antar besaran linier dan angular

Kecepatan tangensial dan kecepatan sudut

Percepatan tangensial dan kecepatan sudut

Kecepatan sudut tidak tetap

Kecepatan sudut

Gerak Berubah Beraturan

Contoh Soal dan Jawaban Sentripetal

1. Sebuah benda bergerak dengan kelajuan tetap v melalui lingkaran berjari-jari r dengan percepatan sentripetal as. a) Agar percepatan sentripetalnya menjadi dua kali semula, maka? b) Apabila v dijadikan 4 kali semula dan r dijadikan 2 kali semula, maka as menjadi?

2. Sebuah benda bermassa 1 kg berputar dengan kecepatan sudut 120 rpm. Jika jari-jari putaran benda adalah 2 meter tentukan percepatan sentripetal gerak benda tersebut !

3. Gaya sentripetal yang bekerja pada sebuah benda bermassa 1 kg yang sedang bergerak melingkar beraturan dengan jari-jari lintasan sebesar 2 m dan kecepatan 3 m/s adalah….?

4. Nyatakan dalam satuan radian : a) 90o b) 270o

5. Sebuah benda bergeak melingkar dengan kecepatan sudut 50π rad/s. Tentukan frekuensi putaran gerak benda!

6. Gaya sentripetal yang bekerja pada sebuah benda bermassa 1 kg yang sedang bergerak melingkar beraturan dengan jari-jari lintasan sebesar 2 m dan kecepatan 3 m/s adalah….?

7. Kecepatan sudut sebuah benda yang bergerak melingkar adalah 12 rad/s. Jika jari-jari putarannya adalah 2 meter, tentukan besar kecepatan benda tersebut!

8. Dua buah roda berputar dihubungkan seperti gambar berikut!

9. Sebuah partikel bergerak melingkar dengan kecepatan sudut sebesar 4 rad/s selama 5 sekon. Tentukan besar sudut yang ditempuh partikel tersebut!

11. Dua buah roda berputar dihubungkan seperti gambar berikut!

12. Roda sebuah mobil selalu melakukan 120 putaran setiap 60 sekon. Berapa kelajuan sudut roda ? Nyatakan dalam: (a) revolution per minute (rpm) atau putaran per menit (b) derajat per sekon (o/s) (c) radian per sekon (rad/s)

13. Tiga buah roda berputar dihubungkan seperti gambar berikut!

14. Sebuah benda bergerak melingkar dengan percepatan sudut 2 rad/s2. Jika mula-mula benda diam, tentukan : a) Kecepatan sudut benda setelah 5 sekon b) Sudut tempuh setelah 5 sekon

15. Konversikan ke dalam satuan rad/s : a) 120 rpm b) 60 rpm

17. Jika kelajuan sudut roda berjari-jari 20 cm adalah 120 rpm, berapa jarak tempuh mobil ketika bergerak selama 10 sekon?

18. Sebuah benda memiliki massa 100 g bergerak melingkar beraturan dengan kelajuan 3 m.s−1. Jika jari-jari lintasan benda adalah 40 cm maka gaya sentripetal yang dialami benda tersebut sebesar…. A. 1,25 N B. 2,25 N C. 3,25 N D. 4,25 N E. 5,25 N

Rumus Fisika Lainnya

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

1. Sebuah benda bergerak dengan kelajuan tetap $v$ melalui lingkaran berjari-jari $r$ dengan percepatan sentripetal $a_{s}$ .
a) Agar percepatan sentripetalnya menjadi dua kali semula, maka?
b) Apabila $v$ dijadikan 4 kali semula dan $r$ dijadikan 2 kali semula, maka a_s menjadi?

4. Nyatakan dalam satuan radian :
a) 90^o
b) 270^o

12. Roda sebuah mobil selalu melakukan 120 putaran setiap 60 sekon. Berapa kelajuan sudut roda ? Nyatakan dalam:
(a) revolution per minute (rpm) atau putaran per menit
(b) derajat per sekon (^o/s)
(c) radian per sekon (rad/s)

14. Sebuah benda bergerak melingkar dengan percepatan sudut 2 rad/s². Jika mula-mula benda diam, tentukan :
a) Kecepatan sudut benda setelah 5 sekon
b) Sudut tempuh setelah 5 sekon

15. Konversikan ke dalam satuan rad/s :
a) 120 rpm
b) 60 rpm

18. Sebuah benda memiliki massa 100 g bergerak melingkar beraturan dengan kelajuan 3 m.s⁻¹. Jika jari-jari lintasan benda adalah 40 cm maka gaya sentripetal yang dialami benda tersebut sebesar….
A. 1,25 N B. 2,25 N C. 3,25 N D. 4,25 N E. 5,25 N