Persentase
Dalam matematika, persentase atau perseratus adalah adalah sebuah angka atau perbandingan (rasio) untuk menyatakan pecahan dari seratus. Persentase sering ditunjukkan dengan simbol “%” unuk menghitung persen.
Persentase juga digunakan meskipun bukan unsur ratusan. Bilangan itu kemudian diskalakan agar dapat dibandingkan dengan seratus.
Contohnya, 4 orang dosen sedang mengawas ujian di kampus, 3 dari mereka tak berkacamata, dan 1 orang berkacamata. Persentase dosenyang tidak berkacamata adalah 3 dari 4 = 3/4 = 75/100 = 75%, sementara dosen berkacamata adalah 1 dari 4 = 1/4 = 25/100.
Rumus Persen
Rumus menghitung persen
Persentase (%) = (bagian/seluruh) x 100
Rumus menghitung nilai persen
Nilai persen = [Nilai Persen] x [100] x [Nilai Pecahan] Nilai persen = [Nilai Persen] x [Nilai Pecahan] : [100]
Rumus mencari nilai persen (%)
Persen = [Nilai] : [Nilai Pecahan] x [100] Harga Diskon = Harga Awal x Persentase Diskon.
Rumus menghitung persentase untung
% Untung = untung / harga beli x100%
Rumus menghitung untung jika diketahui persen untung dan harga beli
Untung = %untung / 100 x harga beli
Rumus menghitung persentase rugi
% Rugi = rugi / harga beli x 100
Rumus menghitung rugi jika diketahui persen rugi dan harga beli
Rugi = %rugi / 100 x Harga beli
Rumus untuk menghitung harga jual dengan persentase keuntungan tertentu
Harga jual = [100 + %untung] / 100 x Harga beli
Rumus untuk menghitung harga beli yang diketahui persentase keuntungan dan harga jualnya
Harga beli = 100 / [100 + %untung] x Harga jual
Rumus untuk menghitung harga jual dengan persentase kerugian tertentu
Harga jual = [100 – rugi] / 100 x Harga jual
Rumus untuk menghitung harga beli yang diketahui persentase kerugian dan harga jualnya
Harga beli = 100 / [100 – %rugi] x Harga jual
Sejarah perkalian menghitung persen
Saat zaman Romawi Kuno, jauh sebelum munculnya sistem desimal yang memungkinkan menuliskan angka dengan ada angka di belakang koma, perhitungan untuk angka-angka tertentu sering di buat dalam fraksi-fraksi kelipatan 1/100.
Di zaman romawi kuno dikenal adanya pajak lelang yang dihitung sebesar 1/100 dari nilai lelang yang dikenal dengan nama centesima rerum venalium. Perhitungan ini mirip dengan istilah persen yang kita kenal pada komputasi modern.
Pada abad-abad berikutnya, istilah pembagi 1/100 ini kemudian sering digunkan dalam berbagai penghitungan. Ia digunakan untuk mencari bagian dari sebuah bagian besar. Di akhir abad ke-15 persen sudah umum digunakan pada berbagai laporan seperti laporan laba rugi, suku bunga, penjualan, dan lain-lain.
Pada abad ini pula penulisan persen mengalami perubahan. Dulu dituliskan dengan kata “percento” kemudian kata “per” digantikan oleh tanda miring “/” dan cento digantikan oleh dua tanda nol (0) yang kemudian kita kenal luas simbolnya persen sebagai “%”.


Pengubahan pecahan ke desimal, desimal ke persen dan sebaliknya
1. Mengubah Pecahan Biasa ke Desimal
Contoh:
2. Mengubah Pecahan Desimal ke Persen
Contoh:
c) Mengubah persen ke pecahan dan sebaliknya
Contoh:
Nyatakan ke dalam pecahan atau ke dalam persen!
Contoh soal persen dan jawabannya
1. Saya membeli meja senilai 100.000, ternyata meja itu ada yang cacat dan tidak bisa ditukar maka saya jual dengan harga 67.000. Berapa persentase kerugian saya?
Cara menghitung persen kerugiannya
jumlah kerugian/harga beli x 100%
100.000-67.000/100.00 x 100% = 33%
2. Tina seorang pedagang, Tina membeli gula perkilonya 9800. Jika Tina menginginkan untung 20% maka berapa gula tersebut harus Tina jual lagi?
Anda bisa saja menghitung nilai keuntungan yang 20% nya dulu baru kemudian ditambahkan dengan 9.800. atau dengan cara yang lebih cepat: [120%/100%] x 9800 = 11 760
120%
—– x 9.800 = 11.760
100%
3. Budi membeli satu baju seharga Rp 125.000 dan memperoleh diskon sebesar 40%. Berapa total biaya yang patut di bayar oleh Budi?
Jawaban
Diketahui:
Harga mula-mula = Rp. 200.000
Harga diskon = harga mula-mula x persentase diskon
Harga diskon = Rp. 200.000 x 40%
Harga diskon = Rp. 200.000 x 40/100
Harga diskon = Rp. 80.000
Ditanyakan:
Harga akhir = … ?
Harga akhir = harga mula – harga diskon
Harga akhir = Rp. 200.000 – Rp. 80.000
Harga akhir = Rp. 120.000
Maka total biaya yang harus dibayar Budi agar bisa membeli baju itu ialah Rp. 120.000
4. Jika sebuah topi seharga Rp40.000,00 didiskon menjadi Rp32.000,00, berapa persen diskon yang diberikan?
Persentase tidak diketahui, Rp40.000 adalah nilai awal dan Rp32.000 adalah nilai baru.
Untuk menjawab contoh soal, ketik bilangan 32.000, tekan simbol pembagian, ketik bilangan 40.000, lalu tekan simbol sama dengan.
Hasil yang muncul yaitu: 0,8 (ini bukan jawaban akhir)
Ubah 0,8 menjadi 80%.
Bandingkan persentase tersebut dengan 100%. Jika persentase kurang dari 100%, terjadi penurunan atau diskon. Jika persentase melebihi 100%, terjadi kenaikan.
Karena harga baru lebih kecil daripada harga awal dan yang ditanyakan memang diskon, penghitungan kita sejauh ini benar. Sebaliknya, jika didapat hasil 120%, pasti penghitungan kita salah karena soal menanyakan diskon sehingga tidak mungkin ada kenaikan (lebih dari 100%).
Hitung selisih persentase dengan 100%. Selisih tersebut merupakan jawaban akhir. Pada contoh soal, ada selisih 20% antara 80% dengan 100%. Jadi, harga awal topi didiskon sebesar 20%.
5. Kemeja seharga Rp120.000 didiskon 65%. Berapa harga yang baru?
Jawaban: 100% – 65% = 35%; ubah 35% menjadi 0,35.
0,35 x 120.000 = 42.000. Jadi, setelah didiskon 65%, harga kemeja menjadi Rp42.000,00 (cukup murah!)
6. Sebuah populasi yang terdiri dari 4.800 orang mengalami pertumbuhan sebesar 20%. Berapa jumlah orang sekarang?
Jawaban: 100% + 20% = 120%; ubah 120% menjadi 1,2.
1,2 x 4.800 = 5.760. Jadi, dalam koloni tersebut, ada 5.760 orang sekarang.
7. Nilai sebuah investasi naik sebesar 22% sehingga sekarang bernilai Rp1.525.000,00. Berapa nilai awal investasi tersebut?
Soal ini melibatkan persentase kenaikan. Jadi, jumlahkan 100% dengan 22% sehingga didapat hasil 122%.
Ubah 122% menjadi bilangan desimal: 1,22.
Ambil kalkulator. Ketik bilangan 1.525.000, tekan simbol pembagian, ketik bilangan 1,22, tekan simbol sama dengan; didapat hasil 1.250.000.
Tulis kalimat jawaban yang tepat. Jadi, nilai awal investasi tersebut adalah Rp1.250.000,00.
8. Jika Anda menerima gaji Rp45.000.000 per tahun di pekerjaan Anda sebelumnya, lalu Anda menerima jabatan baru dengan gaji Rp50.000.000 per tahun. Berapa persen kenaikan gaji Anda?
Ini berarti Anda harus mengurangi Rp50.000.000 dengan Rp45.000.000 = Rp5.000.000
Rp 5.000.000 / Rp 45.000.000 = 0,111. Ubah angka yang ditulis dalam format desimal menjadi persentase, Anda cukup mengalikannya dengan 100.
0,111 x 100 = 11,1%. Jadi kenaikan gaji Anda 11,1%.
9. Apabila Pak Michael memiliki pinjaman cicilan Rp 120.000.000, dengan ansuran setiap bulan sebesar 3.520.000, selama 47 kali, maka berapa persen angsuran tiap bulan pak Michael terhadap pinjaman?
Berdasarkan masalah atau soal persen diatas kita ketahui tentang jumlah pinjaman Rp.120.000.000
Jumlah angsuran tiap bulan Rp. 3.520.000
Karena ditanyakan persen angsuran setiap bulan, maka nilai yang harus kita cari adalah jumlah kenaikan biaya ansuran atau pinjaman yang dibebankan kepada Pak Andi tiap bulan.
Pertama kita cari nilai pembayaran tiap bulan atau cicilan tiap bulan tanpa adanya bunga pinjaman, yaitu Rp 120.000.000/47 kali ansuran = Rp. 2553191.
Ini merupakan nilai seluruh. Sehingga jumlah kenaikan yang dibebankan atau bunga pinjaman Pak Michael adalah Rp.3.520.000 – Rp. 2.553.191 = Rp.966.809. Nilai rupiah tersebut kemudian di persenkan menggunakan rumus perhitungan persen diatas
Persenan = (bagian/ Seluruh) x 100 % = (Rp. 966.809 / 2553.191) x 100 % = 37, 87 %. Sehingga persen angsuran tiap bulan Pak Michael atau bunga pinjaman Pak Michael setiap bulan itu Rp.966.809, tinggi bukan!.
10. Terdapat botol air minum yang telah terisi air 200 ml. Selanjutnya Anda menambahkan air sebanyak 40 ml. Berapa persentase kenaikan volume air dalam botol?
Diketahui bagian adalah 40 ml. Seluruh adalah 200 ml.
Rumus: Bagian = (persentase/100 %) x seluruh
Sehingga menggunakan rumus persen diatas yaitu persentase = (40 ml / 200 ml) x 100 % = 20 %.
11. Terdapat 10 buah Appel. Bila Budi mengambil 2 appel, berapa persen yang tersisa?
Seluruh adalah 10 Appel, sedangkan yang diambil ada 2 appel, sehingga tersisa 10-2 appel=8 appel.
Rumus: Bagian = (persentase/100 %) x seluruh
Persenan = (Bagian/Seluruh) x 100 % = (8/10) x 100 % = 80 %. Jadi, tersisa 80 % appel.
Bila pertanyaan tentang persenan diatas diubah, yaitu berapa persen yang diambil Andi, Anda dapat menggunakan cara menghitung persen diatas barusan, dapat juga dengan langsung saja mengurangi 100 %-80 % menjadi 20 %.
12. Ibu Linda hendak membeli satu buah meja baru, setelah memilih meja yang ia mau, Ibu Linda kemudian mendatangi si kasir untuk membayar meja tersebut. Seusai dikasih potongan harga dengan jumlah 40% harga meja tersebut jadi Rp. 650.000. Hitunglah berapa harga awal dari meja tersebut sebelum dikasih diskon?
Penyelesaian
Diketahui:
Harga akhir = Rp. 650.000
persentase diskon = 50 %
Ditanyakan:
Harga mula-mula = …?
Pakai Logika perbandingan :
X% +Y% = Z %
50% + 50 % = 100 %
Rp X + Rp 650,000 = Rp Z
(Rp 650.000 x 50%) : 50 % = Rp 650,000
Maka Harga mula-mula ialah Rp 650,000 + Rp 650,000 = Rp 1,300,000
Maka harga mula-mula dari meja tersebut sebelum dipotong diskon ialah Rp 1,300,000.
13. Harga sepeda motor = Rp 14 Juta, DP = 4 Juta, lama cicilan = 36 Bulan (3 tahun), berapa persen bunganya ?
Bunga total (36 bulan) = Rp 400.000 x 36 = Rp 14.400.000
Bunga total (36 bulan) = Rp 14.400.000 – Rp 10.000.000 = Rp 4.400.000
Bunga total (36 bulan) = Rp 4.400.000 / 36 = Rp 122.222,-
Persentase Bunga = Rp 122.222 / Rp 10.000.000 = 0,012 atau 1,2% per bulan.
Total jumlah persentase bunga ini kira-kira sudah meliputi premi asuransi. Besar bunga dalam 1 tahun, 2 tahun atau 3 tahun pastinya juga akan berbeda.
14. Sebuah barang dibeli dengan harga Rp. 2.000.000,00 dan di jual dengan harga Rp. 2.400.000,00. Hitunglah persentase keuntungan dari harga pembelian dan dari harga penjualan!
Jawaban:
Laba = Rp. 2.400.000,00 – Rp. 2.000.000,00 = Rp. 400.000,00
Persentase keuntungan (laba) dari harga beli:
Persentase keuntungan (laba) dari harga penjualan:
15. Perusahaan Holiday Sport mengorganisir penjualan luar biasa untuk semua perlengkapan musim dinginnya, dengan pengurangan 65% dari harga normal. Anda telah menemukan jaket snowboard yang Anda inginkan selama setahun. Itu $ 220 sebelum penjualan. Berapa biayanya sekarang?
Temuan bagus! Nah, jaket ini diskon 65% dari $ 220. Pertama kita perlu mencari tahu apa itu 65% dari 220. Mari kita terjemahkan ini ke dalam persamaan:
Berapakah (x) (=) 65% (0,65) dari (kalikan) 220?
x = 0,65 × 220
Sekarang selesaikan persamaannya.
x = 0,65 × 220 = 143
16. Seorang salesman TV akan mendapatkan komisi sebesar 15 % jika ia mampu menjual barang senilai Rp. 2.000.000,00. Berapa besarnya komisi yang diterima?
Jawaban:
Komisi = 15 % x Rp. 2.000.000
Jadi besarnya komisi yang diterima oleh salesman itu sebesar. Rp. 300.000,00
17. Beras dibeli dengan harga Rp.168.000,00 per-50kg, kemudian dijual harga Rp.2.100,00 tiap ½ kg. Persentase keuntungan dari harga pembelian adalah…
a) 10%
b) 15%
c) 23%
d. 30%
e. 35%
Jawaban: c 25%
Cara menghitung Untung = harga jual – harga beli
= Rp.210.000,00 – Rp.168.000,00
= Rp. 42.000,00
% Untung = U
H.B
= Rp. 42.000,00 x 100% = 25%
Rp. 168.000,00
18. Berapa 10% dari 150?
Ubah soal menjadi persamaan menggunakan rumus persentase: P% * X = Y
P adalah 10%, X adalah 150, jadi persamaannya adalah 10% * 150 = Y
Ubah 10% menjadi desimal dengan menghilangkan tanda persen dan membaginya dengan 100: 10/100 = 0,10
Gantikan 0,10 untuk 10% dalam persamaan: 10% * 150 = Y menjadi 0,10 * 150 = Y
Lakukan perhitungan: 0,10 * 150 = 15
Y = 15
Jadi 10% dari 150 adalah 15
Periksa kembali jawaban Anda dengan pertanyaan asli: Berapa 10% dari 150? Kalikan 0,10 * 150 = 15
18. Pertanyaan: 24% dari ___ adalah 36
Jawaban:
36 / dari = 24/100
Gantikan dengan y dan kalikan silang untuk mendapatkan:
36 / y = 24/100
y × 24 = 36 × 100
y × 24 = 3600
Bagilah 3600 dengan 24 untuk mendapatkan y
3600/24 = 150, y = 150
Oleh karena itu, 24% dari 150 adalah 360
Tentang Matematika
- Tes Matematika Deret Angka Untuk Yang Pintar – Tomat, Timun Dan Paprika
- Tes Matematika “Otak Atik Otak” Jumlah nomor yang harus didapatkan: 50 & Nomor yang diberikan: 2 8 9 15 20 40
- Tes Matematika Pengukuran Berat: Sebuah botol & tutupnya berberat 110g. Berat botol 100g lebih berat daripada tutupnya. Berapa berat tutupnya?
- Matematika Jika 2=6, 3=15, 4=24, 5=35, 6=48 Jadi 7=??
- Tes Matematika Pemecahan Masalah Logika Visual Psikotes Roda Gigi X – Beserta Rumus, Soal & Jawaban Untuk Menghitung Panjang Lintasan Roda
- Rumus Trigonometri Dan Contoh-Contoh Soal Beserta Jawabannya
- Soal Rumus Kimia Hidrat (Air Kristal) Dan Jawabannya
- Induksi Matematika Rumus, Contoh Soal dan Jawaban
Bacaan Lainnya
- Berapa Kecerdasan IQ Anda? Tes IQ Anda Disini
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
- Tulisan Menunjukkan Kepribadian Anda & Bagaimana Cara Anda Menulis?
- Top 10 Sungai Terpanjang Di Dunia
- Perbedaan Ketelitian, Ketepatan Dan Kecermatan Pada Kalkulasi & Cara Untuk Mencegah Kesalahan Menghitung
Sumber: Helping With Math
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing

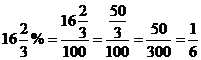
Wah rumus dan contoh soal lengkap. Makasih ya Admin ??
Sama-Sama Kelly 🙂
Mohon penjelasan contoh soal yang ini.
3. Budi membeli satu baju seharga Rp 125.000 dan memperoleh diskon sebesar 40%. Berapa total biaya yang patut di bayar oleh Budi?
Jawaban
Diketahui:
Harga mula-mula = Rp. 200.000
Harga diskon = harga mula-mula x persentase diskon
Harga diskon = Rp. 200.000 x 40%
Harga diskon = Rp. 200.000 x 40/100
Harga diskon = Rp. 80.000
Ditanyakan:
Harga akhir = … ?
Harga akhir = harga mula – harga diskon
Harga akhir = Rp. 200.000 – Rp. 80.000
Harga akhir = Rp. 120.000
Maka total biaya yang harus dibayar Budi agar bisa membeli baju itu ialah Rp. 120.000.
poin utama yang jadi pertanyaan adalah darimana dapat harga semula Rp. 200.000 itu…???
Terima kasih.
Ndak semua betul jawabanya
Penghitungan untuk contoh soal nomor 7 kl menggunakan rumus bagaimana…???
(Nilai sebuah investasi naik sebesar 22% sehingga sekarang bernilai Rp1.525.000,00. Berapa nilai awal investasi tersebut?
Soal ini melibatkan persentase kenaikan. Jadi, jumlahkan 100% dengan 22% sehingga didapat hasil 122%.
Ubah 122% menjadi bilangan desimal: 1,22.
Ambil kalkulator. Ketik bilangan 1.525.000, tekan simbol pembagian, ketik bilangan 1,22, tekan simbol sama dengan; didapat hasil 1.250.000.
Tulis kalimat jawaban yang tepat. Jadi, nilai awal investasi tersebut adalah Rp1.250.000,00.)
Kita tiadakan penggunaan kalkulator. Kita fokus pada penggunaan rumus saja.
Bagaimana…???
Terima kasih.
soal no 3 dengan penjelasan yang berbeda, harga mula2+125k bukan 200k. saya hitung menggunakan cara sendiri, 2 kali hitung tnpa lihat jawaban nya anda ternyata harga mula2 nya salah. ><