Rumus Trigonometri dan Hubungan Fungsi
Berikut adalah rumus trigonometri dan hubungan fungsi:
Fungsi dasar rumus trigonometri:
Identitas Trigonometri
Baca selanjutnya tentang identitas rumus trigonometri di ? Identitas Trigonometri – Rumus, Penjelasan, Pembuktian, Contoh Soal dan Jawaban
Rumus jumlah dan selisih sudut
Rumus perkalian trigonometri
2sinAcosB = sin(A+B) + sin(A-B)
2cosAsinB = sin(A+B) – sin(A-B)
2cosAcosB = cos(A+B) + cos(A-B)
2sinAsinB = -cos(A+B) + cos(A-B)
Rumus jumlah dan selisih trigonometri
Rumus trigonometri sudut rangkap 2
Rumus trigonometri sudut rangkap 3
sin3A = 3sinA – 4sin3A
cos3A = 4cos3A – 3cosA
Rumus setengah sudut
- 1. Jika f(x) = sin x maka f'(x) = cos x
2. Jika f(x) = cos x maka f'(x) = -sin x
3. Jika f(x) = tan x maka f'(x) = sec²x
4. Jika f(x) = cot x maka f'(x) = -cosec²x
5. Jika f(x) = sec x maka f'(x) = sec x.tan x
6. Jika f(x) = cosec x maka f'(x) = -cosec x.cot x
Baca selanjutnya tentang turunan fungsi trigonometri di ? Turunan Trigonometri – Rumus Turunan Fungsi Trigonometri – Contoh Soal dan Jawaban
Rentang Sudut Kuadran Trigonometri

- Kuadran 1 memiliki rentang sudut dari 0° – 90° dengan nilai sinus, cosinus dan tangent positif.
- Kuadran 2 memiliki rentang sudut dari 90° – 180° dengan nilai cosinus dan tangen negatif, sinus positif.
- Kuadran 3 memiliki rentang sudut dari 180° – 270° dengan nilai sinus dan cosinus negatif, tangen positif.
- Kuadran 4 memiliki rentang sudut dari 270° – 360° dengan nilai sinus dan tangent negatif, cosinus positif.
Sudut Istimewa Rumus Trigonometri
Sudut istimewa sendiri merupakan sudut-sudut yang mempunyai nilai derajat tertentu seperti 0°, 30°, 45°, 60°, 90° dan lain-lain; dapat di tentukan oleh tabel yang ada di bawah ini.
Sudut Istimewa Kuadran I
| 0° | 30° | 45° | 60° | 90° | |
| sin | 0 | 1/2 | 1/2√2 | 1/2√3 | 1 |
| cos | 1 | 1/2√3 | 1/2√2 | 1/2 | 0 |
| tan | 0 | 1/3√3 | 1 | √3 | ∞ |
Sudut Istimewa Kuadran II
| 90° | 120° | 135° | 150° | 180° | |
| sin | 0 | 1/2√3 | 1/2√2 | 1/2 | 0 |
| cos | 1 | –1/2 | –1/2√2 | –1/2√ | -1 |
| tan | ∞ | –√3 | -1 | –1/3√3 | 0 |
Sudut Istimewa Kuadran III
| 180° | 210° | 225° | 240° | 270° | |
| sin | 0 | –1/2 | –1/2√2 | –1/2√3 | 1 |
| cos | 1 | –1/2 √3 | –1/2 √2 | –1/2 | 0 |
| tan | 0 | 1/3 √3 | 1 | √3 | ∞ |
Sudut Istimewa Kuadran IV
| 270° | 300° | 315° | 330° | 360° | |
| sin | -1 | –1/2 √3 | –1/2 √2 | –1/2 | 0 |
| cos | 0 | 1/2 | 1/2 √2 | 1/2 √3 | 1 |
| tan | ∞ | -√3 | -1 | –1/3 √3 | 0 |
Baca selanjutnya tentang sudut istimewa di ? Sudut Istimewa Sampai 360 – Trigonometri – Soal dan Jawaban
Rumus trigonometri perbandingan untuk sudut-sudut berelasi
Hanya ada beberapa aturan yang harus diingat:
⇒ Untuk sudut (90 ± a) dan (270 ± a) berlaku: sin = cos, cos = sin,
tan = cot, cot = tan, sec = cosec, cosec = sec ; dengan tanda positif
dan negatif disesuaikan berdasarkan ASTC.
⇒ Untuk sudut (180 ± a) dan (360 ± a) berlaku: sin = sin, cos = cos,
tan = tan, cot = cot, sec = sec, cosec = cosec ; dengan tanda positif
dan negatif disesuaikan berdasarkan ASTC.
Persamaan trigonometri
x = α + k360 atau x = (180 – α) +k360
x = ± α + k360
x = α + k180
Identitas Trigonometri – Rumus Dasar Identitas
Rumus rumus dasar identitas trigonometri sebagai berikut:
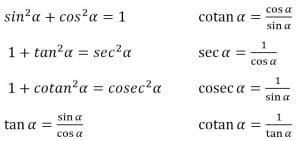
Untuk membuktikan suatu persamaan mempakan identitas atau bukan maka persamaan itu diubah dengan salah satu dari cara-cara berikut:
- Mengubah bentuk ruas kiri sehingga menjadi bentuk ruas kanan.
- Mengubah bentuk ruas kanan, sehingga menjadi bentuk ruas kiri.
- Mengubah bentuk ruas kiri maupun ruas kanan sehingga menjadi bentuk yang sama.
Perkalian, Penjumlahan dan Pengurangan Sinus dan Kosinus
Rumus Perkalian Sinus dan Kosinus
- 2 sin A sin B = cos (A- B) – cos (A+ B)
- 2 sin A cos B = sin (A + B) + sin (A-B)
- 2 cos A sin B = sin (A + B)-sin (A-B)
- 2 cos A cos B = cos (A + B) + cos (A- B)
Rumus Penjumlahan dan Pengurangan Sinus dan Kosinus
- sin A + sin B = 2sin ½ (A+B) cos ½ (A-B)
- sin A – sin B = 2cos ½ (A+B) sin ½ (A-B)
- cos A + cos B = 2cos ½ (A+B) cos ½ (A-B)
- cos A – cos B = -2sin ½ (A+B) cos ½ (A-B)
- tan A + tan B =

- tan A – tan B =

Kegunaan Triginometri Dalam Kehidupan Sehari-Hari
1. Sebagai teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat.
2. Dalam geografi untuk menghitung antara titik tertentu dan dalam sistem navigasi satelit.
3. Dalam kriminologi, trigonometri dapat membantu menghitung lintasan proyektil, untuk memperkirakan apa yang mungkin menyebabkan tabrakan dalam kecelakaan mobil atau bagaimana benda jatuh dari suatu tempat atau di mana sudut tembakan peluru, dll.
4. Dalam konstruksi kita membutuhkan trigonometri untuk menghitung? Mengukur bidang, banyak dan area? Membuat dinding sejajar dan tegak lurus? memasang ubin keramik, kecenderungan atap, tinggi bangunan, panjang lebar dan sebagainya. Banyak hal lain lainnya yang menjadi kebutuhan untuk menggunakan trigonometri.
5. Arsitek menggunakan trigonometri untuk menghitung beban struktural, lereng atap, permukaan tanah dan banyak aspek lainnya, termasuk naungan matahari dan sudut cahaya.
6. Bidang lainnya yang menggunakan trigonometri:
- Termasuk astronomi (dan termasuk navigasi, di laut, udara dan angkasa)
- Teori musik, akustik
- Teori optik
- Analisis pasar finansial
- Elektronik
- Teori probabilitas
- Statistika
- Biologi
- Pencitraan medis/medical imaging (CAT scan dan ultrasound)
- Farmasi
- Kimia
- Teori angka (dan termasuk kriptologi)
- Seismologi
- Meteorologi
- Oseanografi
- Berbagai cabang dalam ilmu fisika
- Survei darat dan geodesi
- Arsitektur
- Fonetika
- Ekonomi
- Teknik listrik
- Teknik mekanik
- Teknik sipil
- Grafik komputer
- Kartografi
- Kristalografi
Penjelasan Trigonometri
Trigonometri adalah sebuah cabang matematika yang berhadapan dengan sudut segitiga dan fungsi trigonometrik seperti sinus, cosinus dan tangen. Dibawah ini Anda dapat menemukan rumus trigonometri beserta contoh soal dan jawabannya.
Trigonometri berasal dari bahasa Yunani: trigonon = tiga sudut dan metro = mengukur.
Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.
Sejarah awal
Awal trigonometri dapat dilacak hingga zaman Mesir Kuno dan Babilonia dan peradaban Lembah Indus, lebih dari 3000 tahun yang lalu. Matematikawan India adalah perintis penghitungan variabel aljabar yang digunakan untuk menghitung astronomi dan juga trigonometri.
Konsep Trigonometri
Dasar dari Trigonometri adalah Konsep kesebangunan segitiga siku-siku. Sisi-sisi yang bersesuaian pada dua bangun datar yang sebangun memiliki perbandingan yang sama.
Pada geometri Euclid, jika masing-masing sudut pada dua segitiga memiliki besar yang sama, maka kedua segitiga itu pasti sebangun. Hal ini adalah dasar untuk perbandingan trigonometri sudut lancip. Konsep ini lalu dikembangkan lagi untuk sudut-sudut non lancip (lebih dari 90 derajat dan kurang dari nol derajat).
Contoh Soal dan Jawaban Trigonometri
1. Tentukan luas segitiga:

Luas segitiga = ½ 3.5. sin 30o = ½.3.5.½ = 15/4 = 3,75 cm
2. Titik P dan Q dinyatakan dengan kordinat polar. Tentukan jarak antar titik Pdan Q.
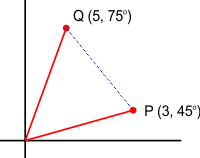
Jawaban:
Dari gambar di atas terlihat bentuk segitiga dan jarak antar titik P dan Q bisa dicari dengan menggunakan aturan cosinus.
Besar sudut POQ = 180o – (75o+45o) = 60o.
PQ2 = OQ2 + OP2 – 2.OQ.OP cos ∠POQ
PQ2 = 32 + 52 – 2.3.5 cos 60o c
PQ2 = 9 + 25 – 30. 0,5
PQ2 = 9 + 25 -15
PQ2 = 19
PQ = √19 = 4,36
3. Berapa nilai sin 120o?
Jawaban:
120 = 90 + 30, jadi sin 120o dapat dihitung dengan
Sin 120o = Sin (90o + 30o) = Cos 30o (nilainya positif karena soalnya adalah sin 120o, di kuadran 2, maka hasilnya positif)
Cos 30o = ½ √3
Atau dengan cara lain:
Sama seperti 180o-80o.
Sin 120o = Sin (180o – 60o) = sin 60o = ½ √3
4. Tentukan nilai dari: 2 cos 75° cos 15°
Jawaban:
2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)°
= cos 90° + cos 60°
= 0 + ½
= ½
5. Buktikan bahwa sin4 α – sin2 α = cos4 α – cos2 α
Jawaban:
sin4 α – sin2 α = (sin2 α)2 – sin2 α
= (1 cos2 α) 2 – (1 cos2 α)
= 1 – 2 cos2 α + cos4 α – 1 + cos2 α
= cos4 α – cos2 α
6. Diketahui p dan q adalah sudut lancip dan p – q = 30°. Jika cos p sin q = 1/6 , maka nilai
dari sin p cos q =
Jawaban:
p – q = 30°
sin (p – q)= sin 30°
sin p cos q – cos p sin q = ½
sin p cos q – 1/6 = ½
sin p cos q = ½ + 1/6 = 4/6
jadi nilai sin p cos q = 4/6
7. Pada segitiga ABC lancip, diketahui cos A = 4/5 dan sin B =12/ 13 , maka sin C =
Jawaban:
Karena segitiga ABC lancip , maka sudut A,B dan C juga lancip, sehingga :
cos A = 4/5, maka sin A = 3/5, (ingat cosami, sindemi dan tandesa)
sin B = 12/13, maka cos B = 5/13
A + B + C = 180°, (jml sudut -sudut dalam satu segitiga = 180)
A + B = 180 – C
sin (A + B) = sin (180 – C)
sin A . cos B + cos A.sin B = sin C, (ingat sudut yang saling berelasi : sin(180-x) = sin x)
sin C = sin A.cos B + cos A.sin B
sin C = 3/5.5/13 + 4/5.12/13
sin C = 15/65 + 48/65 = 63/65
8. A dan B titik ujung sebuah terowongan yang dilihat dari C dengan sudut lihat ACB=45˚ ,Jika garis CB =p dan CA=2p√2 , maka panjang terowongan itu adalah…
Jawaban:
Aturan Cosinus
AB²=CB²+CA²-2CA.CB cos C
AB²=p²+(2p√2)²-2(p.2p√2) cos 45˚
AB²=p²+8p²-2(2p²√2)√2/2
AB²=9p²-√2(2p²√2)
AB²=9p²-4p²
AB²=5p²
AB=√5p²
AB=p√5
9. Diketahui segitiga ABC dengan panjang sisi AB=6 cm , besar sudut A=30˚ dan sudut C=120˚,Luas segitiga ABC adalah…
Jawaban:
Panjang CB
a/sinA = c/sinC
a/sin30˚=6/sin120˚
a/sin30˚=6/sin60˚
a/1/2=6/√3/2
a√3/2=3
a=2√3/3 x 3
a=2√3
Luas Segitiga
L=1/2 a x c sin30˚
L=1/2 x 2√3 x 6 x 1/2
L=1/4 x 12√3
L=3√3 cm²
10. Diketahui segitiga ABC dengan panjang sisi AB=6 cm, BC=8 cm AC=7 cm. Nilai cos A adalah…
Jawaban:
Cos A=(AB²+AC²-BC²)/2(AB . AC)
Cos A=6²+7²-8²/2(6 . 7)
Cos A = 36+49-64/2(42)
Cos A=21/84
11. Nilai dari cos 1200˚ adalah…
= cos( 120˚+3.360˚)
12. Pada ∆ ABC diketahui a+b=10 , sudut A=30˚ dan sudut 45˚ , maka panjang sisi b adalah…
a+b=10
a=10-b
Aturan Sinus
a/sin A = b/sin B
10-b/ sin 30 = b/sin 45
10-b/1/2= b/√2/2
√2/2(10-b)=b/2
(10√2-b√2)/2=b/2
5√2-b√2/2=b/2
5√2=b√2/2 + b/2
5√2=(b√2+b)/2
5√2=b(√2+1)/2
b=5√2 x 2/(√2+1)
b=10√2/(√2+1) x (√2-1)/(√2-1)
b=20-10√2
b=10(2-√2)
13.Tentukan penyelesaian persamaan trigonometri berikut ini: sin x0 = sin 250
sin x0 = sin 250, maka diperoleh:
Jawaban:
x = 250 + k.3600 atau x = (1800 ? 250) + k.3600
= 1550 + k.3600
Jadi, x = 250 + k.3600 atau 1550 + k.3600
14. Tentukan penyelesaian persamaan trigonometri berikut ini: sin x0 = sin 500
Jawaban:
sin x0 = sin500, maka diperoleh:
x = 500 + k.3600 atau x = (1800 ? 500) + k.3600
= 1300 + k.3600
Jadi, x = 500 + k.3600 atau 1300 + k.3600
15. Tentukan nilai dari sin 105° + sin 15°
jawab:
sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°
![]()
16. Tentukan nilai dari: 2 cos 75° cos 15°
Jawab:
2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)°
= cos 90° + cos 60°
= 0 + ½
= ½
17. Tentukan himpunan penyelesaian dari persamaan trigonometri berikut ini: sin 2x0 = sin 400, jika x dalam interval 0 ? x ? 3600
Jawaban:
sin 2x0 = sin 400, maka diperoleh:
2x = 400 + k.3600 atau 2x = (1800 ? 400) + k.3600
» x = 200 + k.3600 » 2x = 1400 + k.3600
» x = 700 + k.3600
untuk k = 0 ? x = 200 atau untuk k = 0 ? x = 700
k = 1 ? x = 2000 k = 1 ? x = 2500
Jadi, himpunan penyelesaiannya adalah HP = {200, 700, 2000, 2500}
18. Tentukan himpunan penyelesaian dari persamaan trigonometri berikut ini: sin 3x0 = sin 450, jika x dalam interval 0 ? x ? 3600
Jawaban:
sin 3x0 = sin 450, maka diperoleh:
3x = 450 + k.3600 atau 3x = (1800 ? 4500) + k.3600
» x = 150 + k.3600 atau » 3x = 1350 + k.3600
» x = 450 + k.1200
untuk k = 0 ? x = 150 atau untuk k = 0 ? x = 450
k = 1 ? x = 1350 k = 1 ? x = 1650
k = 2 ? x = 2550 k = 2 ? x = 2850
Jadi, himpunan penyelesaiannya adalah: HP = {150, 450, 1350, 1650, 2550, 2850}
19. Buktikan bahwa sin4 α – sin2 α = cos4 α – cos2 α
Jawaban:
sin4 α – sin2 α = (sin2 α)2 – sin2 α
= (1 cos2 α) 2 – (1 cos2 α)
= 1 – 2 cos2 α + cos4 α – 1 + cos2 α
= cos4 α – cos2 α
20. Turunan pertama dari f(x) = 7 cos (5 – 3x) adalah f ‘ (x) =…
- 35 sin (5 – 3x)
- – 15 sin (5 – 3x)
- 21 sin (5 – 3x)
- – 21 sin (5 – 3x)
- – 35 sin (5 – 3x).
Jawab :
21. Tentukan nilai-nilai perbandingan trigonometri pada titik berikut!
A(-3, 4)
Pembahasan
Kali ini, kita membahas Trigonometri. Khususnya, mencari nilai perbandingan Trigonometri yang meliputi sinus, cosinus, dan tangen dari suatu koordinat cartesius. Rumusnya adalah:
Rumus:
Sin α = y/r
Cos α = x/r
Tan α = y/x
Cosec α = r/y
Sec α = r/x
Cot α = x/y
Yang dimana, untuk mencari nilai r, kita menggunakan teorema phytagoras, yaitu r² = x² + y²
Penyelesaian
A (-3, 4)
r² = x² + y²
r² = -3² + 4²
r² = 9 + 16
r² = 25
r = √25
r = 5
Nilai perbandingan trigonometrinya adalah:
Sin α = 4/5
Cos α = -3/5
Tan α = 4/-3 = -4/3
Cosec α = 5/4
Sec α = 5/-3 = -5/3
Cot α = -3/4
22. Tentukan nilai-nilai perbandingan trigonometri pada titik berikut: B(5, 12)
B (5, 12)
r² = x² + y²
r² = 5² + 12²
r² = 25 + 144
r² = 169
r = √169
r = 13
Nilai perbandingan trigonometrinya adalah:
Sin α = 12/13
Cos α = 5/13
Tan α = 12/5
Cosec α = 13/12
Sec α = 13/5
Cot α = 5/12
23. Tentukan nilai-nilai perbandingan trigonometri pada titik berikut: C(12, -16)
C (12, -16)
r² = x² + y²
r² = 12² + -16²
r² = 144 + 256
r² = 400
r = √400
r = 20
Nilai perbandingan trigonometrinya adalah :
Sin α = -16/20
Cos α = 12/20
Tan α = -16/12
Cosec α = 20/-16 = -20/16
Sec α = 20/12
Tan α = 12/-16 = -12/16
24. Tentukan nilai-nilai perbandingan trigonometri pada titik berikut: D(-15, -8)
D (-15, -8)
r² = x² + y²
r² = -15² + -8²
r² = 225 + 64
r² = 289
r = √289
r = 17
Nilai perbandingan trigonometrinya adalah :
Sin α = -8/17
Cos α = -15/17
Tan α = -8/-15 = 8/15
Cosec α = 17/-8 = -17/8
Sec α = 17/-15 = -17/15
Cot α = -15/-8 = 15/8
25. Nyatakan sudut-sudut berikut dalam satuan radian (rad):
a) 270°
b) 330°
Pembahasan dan jawaban:
Konversi:
1 π radian = 180°
Jadi:
a) 270°
= 270° x r/180°
= 3/2 r rad
b) 330°
= 330° x r/180°
= 11/6 r rad
26. Penyelesaian persamaan sin x0 = sin ?0 (x ? R)
Untuk menyelesaiakan persamaan trigonometri sin x0 = sin ?0(x ? R) dapat ditentukan dengan menggunakan hubungan-hubungan yang berlaku pada perbandingan trigonometri sudut berelasi berikut.
- sin (1800-?0) = sin ?0
- sin (?o+k.3600) = sin ?0
Dengan menggunakan hubungan-hubungan di atas, maka penyelesaian persamaan trigonometri sin x0 = sin ?0 dapat ditetapkan sebagai berikut.
| Jika sin x0 = sin ?0 (x ? R), maka:x = ? + k.3600 atau x = (1800 ? ?) + k.360, dengan k ? B Catatan: x dalam derajat Jika sin x = sin A (x ? R), maka: x = A + k.2? atau x = (? ? A) + k.2?, dengan k ? B Catatan: x dalam radian |
Contoh:
Tentukan penyelesaian dari tiap persamaan trigonometri berikut ini:
| a. sin x0 = sin 250 | b. sin x0 = sin 500 |
Jawab:
- sin x0 = sin 250, maka diperoleh:
x = 250 + k.3600 atau x = (1800 ? 250) + k.3600
= 1550 + k.3600
Jadi, x = 250 + k.3600 atau 1550 + k.3600
- sin x0 = sin500, maka diperoleh:
x = 500 + k.3600 atau x = (1800 ? 500) + k.3600
= 1300 + k.3600
Jadi, x = 500 + k.3600 atau 1300 + k.3600
Tentukan himpunan penyelesaian dari tiap persamaan trigonometri berikut ini.
- sin 2x0 = sin 400, jika x dalam interval 0 ? x ? 3600
- sin 3x0 = sin 450, jika x dalam interval 0 ? x ? 3600
Jawab:
- sin 2x0 = sin 400, maka diperoleh:
2x = 400 + k.3600 atau 2x = (1800 ? 400) + k.3600
» x = 200 + k.3600 » 2x = 1400 + k.3600
» x = 700 + k.3600
untuk k = 0 ? x = 200 atau untuk k = 0 ? x = 700
k = 1 ? x = 2000 k = 1 ? x = 2500
Jadi, himpunan penyelesaiannya adalah HP = {200, 700, 2000, 2500}
- sin 3x0 = sin 450, maka diperoleh:
3x = 450 + k.3600 atau 3x = (1800 ? 4500) + k.3600
» x = 150 + k.3600 atau » 3x = 1350 + k.3600
» x = 450 + k.1200
untuk k = 0 ? x = 150 atau untuk k = 0 ? x = 450
k = 1 ? x = 1350 k = 1 ? x = 1650
k = 2 ? x = 2550 k = 2 ? x = 2850
Jadi, himpunan penyelesaiannya adalah:
HP = {150, 450, 1350, 1650, 2550, 2850}
27. Dengan menggunakan identitas trigonometri, sederhanakan setiap bentuk berikut ini: (cos x) / (1+ sin x) + (1+sin x) / (cos x)
cos x/(1 +sin x) +1 +sin x/(cos x)
=cos²x +1 +2sin x +sin²x/(1 +sin x)
(cos x)
=1 -sin²x +1 +2sin x +sin²x/(1 +sin x)
(cos x)
= 2 +2sin x/(1 +sin x) (cos x)
= 2 (1 +sin x) /(1 +sin x) (cos x)
=2/cos x
= 2sec x
28. Jika f(x) = sinx+cosxsinx, sin x ≠ 0 dan f’ adalah turunan f, maka f'(π2) = …
Misalkan:
* u(x) = sin x + cos x , maka:
u'(x) = cos x – sin x
* v(x) = sin x, maka v'(x) = cos x
f(x) = u(x)v(x)
f'(x) = u′(x).v(x)−u(x).v′(x)[v(x)]2
= (cosx−sinx).(sinx)−(sinx+cosx).(cosx)[sinx]2
f'(π2) = (cosπ2−sinπ2).(sinπ2)−(sinπ2+cosπ2).(cosπ2)[sinπ2]2
f'(π2) = (0−1).(1)−(1+0).(0)(1)2
f'(π2) = −1−01
f'(π2) = -1
(JAWABAN: B)
29. Jika f(x) = -(cos² x – sin²x), maka f'(x) adalah…
B. 2(cos x – sin x)
C. sin x. cos x
D. 2sin x cos x
E. 4sin x cos x
f(x) = -(cos² x – sin²x)
f(x) = -((1 – sin²x) – sin²x)
f(x) = -(1 – 2sin²x)
f(x) = 2sin²x – 1
Misalkan:
u(x) = sin x, maka u'(x) = cos x
f(x) = 2[u(x)]² – 1
f'(x) = 4 . u(x)¹. u'(x) – 0
f'(x) = 4 sin x cos x
(JAWABAN: E)
30. Jika iketahui f(x) = sin³ (3 – 2x). Turunan pertama fungsi f adalah f’ maka f'(x) =…
Misalkan:
u(x) = sin (3 – 2x), maka:
u'(x) = cos (3 – 2x) . (-2)
u'(x) = -2cos (3 – 2x)
(-2 berasal dari turunan (3-2x))
f(x) = [u(x)]³
f'(x) = 3[u(x)]² . u'(x)
f'(x) = 3sin²(3 – 2x) . -2cos (3 – 2x)
= -6 sin²(3 – 2x) . cos (3 – 2x)
= -3 . 2 sin (3 -2x).sin (3 -2x).cos (3 – 2x)
= -3 . sin (3 – 2x). 2 sin (3 – 2x).cos (3 – 2x)
(ingat: sin 2x = 2 sin x.cos x)
= -3 sin (3 – 2x) sin 2(3 – 2x)
= -3 sin (3 – 2x) sin (6 – 4x)
(JAWABAN: E)
31. Tentukanlah nilai dari sin 105° + sin 15°
Jawaban:
Dari soal di atas bisa kita simpulkan bahwa jenis soal di atas adalah contoh soal penjumlahan trigonometri.
Sehingga kita dapat melihat rumus penjumlahan sin pada uraian di atas .
Rumusnya yaitu 2sin ½ (A+B) cos ½ (A-B)
Jawaban:
nilai sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°
Maka nilai dari sin 105° + sin 15° adalah sin 60° cos 45°.
32. Apabila tan 5°= p. maka tentukanlah nilai dari: tan 50°
Jawaban:
tan 50° = tan (45° + 5°)
= tan 45° + tan 5°/1 – tan 45° x tan 5°
= 1 + p/1 – p
Sehingga, hasil nilai dari tan 50° adalah = 1 + p/1 – p
Bacaan Lainnya
- Identitas Trigonometri – Rumus, Penjelasan, Contoh Soal dan Jawaban
- Turunan Trigonometri – Rumus Turunan Fungsi Trigonometri – Contoh Soal dan Jawaban
- Integral Trigonometri – Fungsi Beserta Contoh Soal dan Jawaban
- Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
- Trigonometri Invers Beserta Contoh Soal dan Jawaban
- Barisan Aritmetika dan Deret Aritmetika
- Quiz gunung tertinggi di Jepang?
- 24 Foto Yang Menunjukkan Mengapa Wisatawan Memilih Kyoto Sebagai Kota Terbaik Di Dunia
- Cara Membeli Tiket Pesawat Murah Secara Online Untuk Liburan Atau Bisnis
- Tibet Adalah Provinsi Cina – Sejarah Dan Budaya
- Puncak Gunung Tertinggi Di Dunia dimana?
- TOP 10 Gempa Bumi Terdahsyat Di Dunia
- Apakah Matahari Berputar Mengelilingi Pada Dirinya Sendiri?
- Test IPA: Planet Apa Yang Terdekat Dengan Matahari?
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
- TOP 10 Virus Paling Mematikan Manusia
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Pada Daerah Kewanitaan Akibat Pembalut Wanita
- Apakah Produk Pembalut Wanita Aman?
- Narkoba – Contoh, Jenis, Pengertian, Efek jangka pendek dan panjang
- Kepalan Tangan Menandakan Karakter Anda – Kepalan nomer berapa yang Anda miliki?
- 7 Cara Untuk Menguji Apakah Dia, Adalah Teman Sejati Anda Atau Bukan BFF (Best Friend Forever)
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar?Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Sciencing, Clark University, SOS Math
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing


























Nomor 7 itu kurang benar, karena disana tertera sudut abc adalah lancip, sehingga tidak dapat digunakan rumus phytagoras
Maaf saya ingin mencari sambungan soal bab trigonomètri baru halaman 39 udah gak ada
Bikin pening
belajar trigonometri memang butuh perjuangan
Aku ingin jadi wibu fisikawan
Terimakasih ini benar benar membantu???
Sama-sama dan tetap semangat untuk belajar 🙂
Dari dulu trigonometri, memang harus dicoba latihan soal terus, karena mudah lupa rumusnya
Wih keren banget sharingnya. Aduh trigonometri bikin pusing… 🙂