Rumus Mekanika Fluida

Mekanika Fluida adalah cabang dari ilmu fisika yang mempelajari mengenai zat fluida (cair, gas dan plasma) dan gaya yang bekerja padanya. Mekanika fluida dapat dibagi menjadi statika fluida, ilmu yang mempelajari keadaan fluida saat diam; kinematika fluida, ilmu yang mempelajari fluida yang bergerak; dan dinamika fluida, ilmu yang mempelajari efek gaya pada fluida yang bergerak. Ini adalah cabang dari mekanika kontinum, sebuah subjek yang memodelkan materi tanpa memperhatikan informasi mengenai atom penyusun dari materi tersebut sehingga hal ini lebih berdasarkan pada sudut pandang makroskopik daripada sudut pandang mikroskopik.

Rumus Tekanan

$p={\frac {F}{A}}$

Keterangan:

p: Tekanan (N/m² atau dn/cm²)
F: Gaya (N atau dn)
A: Luas alas/penampang (m² atau cm²)

Satuan:

1 Pa = 1 N/m² = 10^-5 bar = 0,99 x 10^-5 atm = 0,752 x 10^-2 mmHg atau torr = 0,145 x 10^-3 lb/in² (psi)
1 torr= 1 mmHg

Tekanan Hidrostatis

$p_{\text{h}}=\rho \,\!\times g\times h$

$p_{\text{h}}=s\times h$

Keterangan:

p_h: Tekanan hidrostatis (N/m² atau dn/cm²)
h: jarak ke permukaan zat cair (m atau cm)
s: berat jenis zat cair (N/m³ atau dn/cm³)
ρ: massa jenis zat cair (kg/m³ atau g/cm³)
g: gravitasi (m/s² atau cm/s²)

Tekanan mutlak dan tekanan gauge

Tekanan gauge: selisih antara tekanan yang tidak diketahui dengan tekanan udara luar.

Tekanan mutlak = tekanan gauge + tekanan atmosfer

$p=p_{\text{gauge}}+p_{\text{atm}}$

Tekanan mutlak pada kedalaman zat cair

$p_{\text{h}}=p_{\text{0}}+\rho \,\!\times g\times h$

Keterangan:

p₀: tekanan udara luar (1 atm = 76 cmHg = 1,01 x 10⁵ Pa)

Hukum Pascal

Tekanan yang diberikan pada zat cair dalam ruang tertutup akan diteruskan sama besar ke segala arah.

${\frac {F_{\text{2}}}{A_{\text{2}}}}={\frac {F_{\text{1}}}{A_{\text{1}}}}$

Keterangan:

F₁: Gaya tekan pada pengisap 1
F₂: Gaya tekan pada pengisap 2
A₁: Luas penampang pada pengisap 1
A₂: Luas penampang pada pengisap 2

Jika yang diketahui adalah besar diameternya, maka: ${F_{\text{2}}}=({\frac {D_{2}}{D_{1}}})^{2}\times F_{1}$

Gaya Apung (Hukum Archimedes)

Gaya apung adalah selisih antara berat benda di udara dengan berat benda dalam zat cair.

$F_{a}=M_{f}\times g$

$F_{a}=\rho _{f}\times V_{bf}\times g$

Keterangan:

F_a: gaya apung
M_f: massa zat cair yang dipindahkan oleh benda
g: gravitasi bumi
ρ_f: massa jenis zat cair
V_bf: volume benda yang tercelup dalam zat cair

Mengapung, tenggelam, dan melayang

Syarat benda mengapung: $\rho _{b}campuran<\rho _{f}$

Syarat benda melayang: $\rho _{b}campuran=\rho _{f}$

Syarat benda tenggelam: $\rho _{b}campuran>\rho _{f}$

Persamaan Navier-Stokes

Bentuk umum persamaan Navier-Stokes untuk kekekalan momentum adalah :

\rho {\frac {D\mathbf {v} }{Dt}}=\nabla \cdot \mathbb {P} +\rho \mathbf {f}

di mana

$\rho$ adalah densitas fluida,

{\frac {D}{Dt}}

adalah derivatif substantif (dikenal juga dengan istilah derivatif dari material)

$\mathbf {v}$ adalah vektor kecepatan,
$f$ adalah vektor gaya benda, dan
$\mathbb {P}$ adalah tensor yang menyatakan gaya-gaya permukaan yang bekerja pada partikel fluida.

$\mathbb {P}$ adalah tensor yang simetris kecuali bila fluida tersusun dari derajat kebebasan yang berputar seperti vorteks. Secara umum, (dalam tiga dimensi) $\mathbb {P}$ memiliki bentuk persamaan:

\mathbb {P} ={\begin{pmatrix}\sigma _{xx}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{yy}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{zz}\end{pmatrix}}

di mana

$\sigma$ adalah tegangan normal, dan
$\tau$ adalah tegangan tangensial (tegangan geser).

Persamaan di atas sebenarnya merupakan sekumpulan tiga persamaan, satu persamaan untuk tiap dimensi. Dengan persamaan ini saja, masih belum memadai untuk menghasilkan hasil penyelesaian masalah. Persamaan yang dapat diselesaikan diperoleh dengan menambahkan persamaan kekekalan massa dan batas-batas kondisi ke dalam persamaan di atas.

Fluida Newtonian vs. non-Newtonian

Sebuah Fluida Newtonian (dinamakan dari Isaac Newton) didefinisikan sebagai fluida yang tegangan gesernya berbanding lurus secara linier dengan gradien kecepatan pada arah tegak lurus dengan bidang geser. Definisi ini memiliki arti bahwa fluida newtonian akan mengalir terus tanpa dipengaruhi gaya-gaya yang bekerja pada fluida. Sebagai contoh, air adalah fluida Newtonian karena air memiliki properti fluida sekalipun pada keadaan diaduk.

Sebaliknya, bila fluida non-Newtonian diaduk, akan tersisa suatu “lubang”. Lubang ini akan terisi seiring dengan berjalannya waktu. Sifat seperti ini dapat teramati pada material-material seperti puding. Peristiwa lain yang terjadi saat fluida non-Newtonian diaduk adalah penurunan viskositas yang menyebabkan fluida tampak “lebih tipis” (dapat dilihat pada cat). Ada banyak tipe fluida non-Newtonian yang kesemuanya memiliki properti tertentu yang berubah pada keadaan tertentu.

Persamaan pada fluida Newtonian

Konstanta yang menghubungkan tegangan geser dan gradien kecepatan secara linier dikenal dengan istilah viskositas. Persamaan yang menggambarkan perlakuan fluida Newtonian adalah:

\tau =\mu {\frac {dv}{dx}}

di mana

\tau

adalah tegangan geser yang dihasilkan oleh fluida

\mu

adalah viskositas fluida-sebuah konstanta proporsionalitas

{\frac {dv}{dx}}

adalah gradien kecepatan yang tegak lurus dengan arah geseran

Viskositas pada fluida Newtonian secara definisi hanya bergantung pada temperatur dan tekanan dan tidak bergantung pada gaya-gaya yang bekerja pada fluida. Jika fluida bersifat inkompresibel dan viskositas bernilai tetap di seluruh bagian fluida, persamaan yang menggambarkan tegangan geser (dalam koordinat Kartesius) adalah

\tau _{ij}=\mu \left({\frac {\partial v_{i}}{\partial x_{j}}}+{\frac {\partial v_{j}}{\partial x_{i}}}\right)

di mana

\tau _{ij}

adalah tegangan geser pada bidang

i^{th}

dengan arah

j^{th}

v_{i}

adalah kecepatan pada arah

i^{th}

x_{j}

adalah koordinat berarah

j^{th}

Jika suatu fluida tidak memenuhi hubungan ini, fluida ini disebut fluida non-Newtonian.

Hukum pendinginan Newton

q = h.A.(Tw-T∞)

Q adalah laju perpindahan panas (satuan SI: watt),
h adalah koefisien perpindahan panas (diasumsikan independen dari T dan dirata-ratakan pada permukaan) (satuan SI: W / m2-K)
A adalah luas permukaan perpindahan panas (satuan SI: m2)
T adalah suhu permukaan benda (satuan SI: K)

Hukum Pendinginan Newton menyatakan bahwa laju perubahan pendinginan suhu suatu benda sebanding dengan perbedaan antara suhu sendiri dan suhu ambien (yaitu suhu sekitarnya). Hukum Newton membuat pernyataan tentang tingkat sesaat perubahan suhu.

Penurunan suhu dalam pendinginan Newton

dT/dt = k ( T-To )

Dimana dT/dt merupakan fungsi temperatur (suhu) terhadap waktu, k adalah konstanta, T adalah suhu pada saat t sekon, dan T0 adalah suhu pada saat t= 0 sekon.

Nilai dari k sendiri tidak diketahui, namun nilainya bisa didapat dengan menurunkan persamaan diatas.(nilai dari k dapat berharga –k dan +k, hal ini dapat ditentukan dengan cara: apabila suhunya mengalami penaikan nilai yang sipakai adalah +k, sebaliknya bila suhu mengalami penurunan maka nilainya adalah -k).

Contoh Soal dan Jawaban dari Rumus Mekanika Fluida

1. Tony mengisi ember yang memiliki kapasitas 20 liter dengan air dari sebuah kran. Jika luas penampang kran dengan diameter D₂ adalah 2 cm² dan kecepatan aliran air di kran adalah 10 m/s tentukan:
a) Debit air
b) Waktu yang diperlukan untuk mengisi ember

Pembahasan
Data :
A₂ = 2 cm² = 2 x 10⁻⁴ m²
v₂ = 10 m/s

a) Debit air
Q = A₂v₂ = (2 x 10⁻⁴)(10)
Q = 2 x 10⁻³ m³/s

b) Waktu yang diperlukan untuk mengisi ember
Data :
V = 20 liter = 20 x 10⁻³ m³
Q = 2 x 10⁻³ m³/s
t = V / Q
t = ( 20 x 10⁻³ m³)/(2 x 10⁻³ m³/s )
t = 10 sekon

2. Tangki air dengan lubang sedang bocor dan air mengalir. Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan:
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah

Pembahasan
a) Kecepatan keluarnya air
v = √(2gh)
v = √(2 x 10 x 3,2) = 8 m/s

b) Jarak mendatar terjauh yang dicapai air
X = 2√(hH)
X = 2√(3,2 x 10) = 8√2 m

c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2H/g)
t = √(2(10)/(10)) = √2 sekon

3. Air dalam bak setinggi 0,2 m terletak 5 m di atas permukaan tanah. Di dasar bak terdapat lubang kran kecil sehingga air memancar keluar dan jatuh di permukaan tanah pada jarak R. Jika g = 10 m.s⁻², nilai R adalah…

A.   2 meter
B.   5 meter
C.   7 meter
D.   10 meter
E.   15 meter

Pembahasan

Misalkan h adalah ketinggian dari permukaan air ke lubang kran dan H adalah ketinggian dari lubang kran ke permukaan tanah.

h = 0,2 m
H = 5 m

Jarak jatuhnya air diukur dari kaki bak (R) dirumuskan sebagai:

R= 2√(hH)
= 2√(0,2 x 5) = 2√1 m

Jadi, jarak mendatar jatuhnya air adalah 2 meter (A).

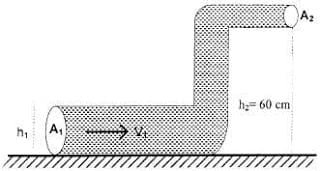
4. Sebuah pipa berbentuk “S” (seperti gambar), dialiri air. Luas penampang besar 10 cm² dan penampang kecil 5 cm². Apabila kecepatan aliran air pada pipa besar 2 m/s² dengan tekanan 40 kilopascal maka tekanan pada pipa kecil adalah …. (ρ_air = 10³ kg/m²)

A.   36 kPa
B.   34 kPa
C.   28 kPa
D.   12 kPa
E.   8 kPa

Pembahasan

Pertama, kita tentukan kecepatan aliran air yang melalui penampang kecil dengan menggunakan rumus debit aliran.

A₁v₁ = A₂v₂
10 × 2 = 5 × v₂
v₂ = 4 m/s

Selanjutnya kita gunakan hukum Bernoulli untuk menyelesaikan soal di atas.

P₁ + ρgh₁ + ½ρv₁² = P₂ + ρgh₂ + ½ρv₂²
4×10⁴ + 10³×10×0 + ½×10³×2² = P₂ + 10³×10×0,6 + ½×10³×4²
40.000 + 2.000 = P₂ + 6.000 + 8.000
42.000 = P₂ + 14.000
P₂ = 28.000

Jadi, tekanan pada pipa yang berpenampang kecil adalah 28 kPa (C).

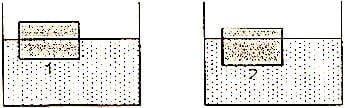
5. Lihatlah gambar dibawah ini. Sebuah benda ketika dimasukkan ke dalam zat cair 1 terapung dengan ½ bagian volumenya berada di bawah permukaan dan ketika dimasukkan ke dalam zat cair 2 terapung ¾ bagian volumenya berada di bawah permukaan, maka perbandingan massa jenis zat cair 1 dan 2 adalah…

A.   3 : 4
B.   3 : 2
C.   2 : 3
D.   1 : 3
E.   1 : 2

Pembahasan

Ketika benda dimasukkan ke dalam cairan 1, ½ bagian volumenya tenggelam, maka:

V₁ = ½V_b

Sehingga massa jenis cairan 1 (ρ₁) adalah:

ρ₁.g.V₁ = ρ_b.g.V_b
ρ₁.½V_b = ρ_b.V_b
ρ₁ = 2ρ_b

Sedangkan ketika benda dimasukkan ke dalam cairan 2, ¾ bagian volumenya tenggelam, maka:

V₂ = ¾V_b

Sehingga massa jenis cairan 2 (ρ₂) adalah:

ρ₂.g.V₂ = ρ_b.g.V_b
ρ₂.¾V_b = ρ_b.V_b
ρ₂ = 4/3ρ_b

Dengan demikian, perbandingan ρ₁ terhadap ρ₂ adalah:

ρ₁ : ρ₂ = 2ρ_b : 4/3ρ_b
= 2 : 4/3
(masing-masing dikalikan 3)
= 6 : 4
= 3 : 2

Jadi, perbandingan massa jenis zat cair 1 dan 2 adalah 3 : 2 (B).

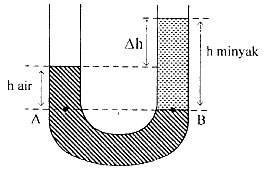
6. Sebuah pipa U diisi minyak dan air dan dalam keadaan stabil tampak seperti gambar. Bila perbedaan ketinggian (Δh) 4,8 cm, tinggi air 7,2 cm, dan massa jenis air 1.000 kg/m³ maka massa jenis minyak adalah…

A.   833 kg/m³
B.   758 kg/m³
C.   666 kg/m³
D.   600 kg/m³
E.   580 kg/m³

Pembahasan

Data yang dapat diperoleh dari soal:
beda ketinggian : Δh = 4,8 cm
tinggi air : h_a = 7,2 cm
massa jenis air : ρ_a = 1.000 kg/m³
tinggi minyak : h_m = h_a + Δh
= 7,2 cm + 4,8 cm
= 12 cm

Tekanan hidrostatis di titik A dan B besarnya sama karena terletak dalam satu garis mendatar.

P_A = P_B
ρ_a g h_a = ρ_m g h_m
ρ_a h_a = ρ_m h_m
1000 × 7,2 = ρ_m × 12
(satuan tidak perlu dikonversi)
ρ_m = 7200/12
= 600

Jadi, massa jenis minyak adalah 600 kg/m³ (D).

7. Berapakah tekanan hidrostatis di dasar kolam dengan kedalaman air 2 m $(\rho_{air}=\text{ 1000 kg/m}^3,\text{g= 10 m/s}^2)$ .

Penyelesaian

Diketahui :
h = 2 m
$\rho_air=\text{ 1000 kg/m}^3)$
g = 10 m/s²

Ditanya : Ph?

Jawaban:
$P_h=\rho.g.h$
= 1000 x 10 x 2
= 20000 N/m²

Jadi tekanan hidrostatis di dasar kolam 20000 N/m²

8. Kapal selam berada pada kedalaman 50 m dibawah permukaan laut. Bila diketahui massa jenis air laut $\text{1,03 x 10}^3\text{kg/m}^3$ dan tekanan udara di atas permukaan laut $10^5$ Pa, berapa tekanan hidrostatis yang dialami kapal selam tsb. ( g = 10 m/s²)

Penyelesaian

Diketahui:
H = 50 m
$\rho_{\text{air laut}}=\text{1,03 x 10}^3\text{ kg/m}^3$
$P_o=10^5\text{ Pa}$
g = 10 m/s²

Ditanya: Ph?

Jawaban:

$P_h=P_o+\rho .g.h$
$P_h=10^5+(1,03.10^3.10.50)$
$P_h=6,15.10^5\text{ Pa}$

9. Sebuah dongkrak hidroulik mempunyai dua penampang masing2 $A_1=10\text{ cm}^2$ dan $A_2=50\text{ cm}^2$ . Jika pada penampang A₁ diberi gaya F₁ = 10 N, berapakah berat beban maksimum yang dapat diangkat oleh penampang A₂?

Penyelesaian

Diketahui :

$A_1=10\text{ cm}^2$
$A_2=50\text{ cm}^2$
$F_1=10\text{ N}$

Ditanya : F2 ?

Jawaban:

$\frac{10}{10}=\frac{F_2}{50}$

$F_2=\frac{10.50}{10}$

$F_2=50\text{ N}$

Jadi berat beban maksimum yang dapat diangkat oleh penampang A2 adalah 50 N

10. Sepotong tembaga volumenya 20 cm³ dan massa jenisnya 9 gr/cm³, dimasukkan ke dalam air yang massa jenisnya 1 gr/cm³. Berapakah berat tembaga di dalam air? ( g= 9,800 cm/s²)

Penyelesaian

Diketahui: V b = 20 cm³ $\rho_{b}=9\text{ gr/cm}^3$
$\rho_{a}=1\text{ gr/cm}^3$
g = 9,800 cm/s²

Ditanya: w ( berat tembaga dlm air)

Jawaban: berat tembaga di udara

$W_u=m_b.g$

$W_u=\rho_b.g.V_b=\text{ 9 x 9800 x 20 = 1764000 dyne}$

Gaya ke atas ( gaya Archimedes)

F = berat air yang dipindahkan
= ma x g
= ρa . g .Va (Va = Vb)
=1 x 9800 x 20
= 196000 dyne

Jadi berat tembaga di dalam air adalah:

Wa = Wu – F

= 1764000 dyne – 196000 dyne
= 1568000 dyne

11. Sebuah jarum terapung di atas air, panjang jarum 5 cm dan memilki massa 5 gr. Tentukan tegangan permukaan air tersebut!

Penyelesaian

Diketahui:

l = 5 cm = 0,05 m
m = 5 gr = 0,005 kg

Ditanya: γ (tegangan permukaan air)

Jawaban:

$\gamma=\frac{F}{2l}$

$\gamma=\frac{mg}{2l}$

$\gamma=\frac{0,005x10}{2x0,05}$

$\gamma=0,5\text{ N/m}$

Jadi tegangan permukaan air sebesar 0,5 N/m

Rumus mekanika fluida — Ilustrasi gambar untuk artikel: Rumus Mekanika Fluida Dan Contoh-Contoh Soal Beserta Jawabannya. Sumber foto: Pexels

Rumus Fisika Lainnya

Fisika banyak diisi dengan persamaan dan rumus fisika yang berhubungan dengan gerakan sudut, mesin Carnot, cairan, gaya, momen inersia, gerak linier, gerak harmonik sederhana, termodinamika dan kerja dan energi. Klik disini untuk melihat rumus fisika lainnya (akan membuka layar baru, tanpa meninggalkan layar ini).

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Physics, Tutor Vista, University of British Columbia

Rumus Mekanika Fluida Tekanan, Hidrostatis, Hukum Pascal, Apung, Navier-Stokes, Fluida Newton | Beserta Contoh-Contoh Soal dan Jawaban

Rumus Mekanika Fluida

Rumus Tekanan

Tekanan Hidrostatis

Tekanan mutlak dan tekanan gauge

Tekanan mutlak pada kedalaman zat cair

Hukum Pascal

Gaya Apung (Hukum Archimedes)

Mengapung, tenggelam, dan melayang

Persamaan Navier-Stokes

Fluida Newtonian vs. non-Newtonian

Persamaan pada fluida Newtonian

Hukum pendinginan Newton

Penurunan suhu dalam pendinginan Newton

Contoh Soal dan Jawaban dari Rumus Mekanika Fluida

1. Tony mengisi ember yang memiliki kapasitas 20 liter dengan air dari sebuah kran. Jika luas penampang kran dengan diameter D₂ adalah 2 cm² dan kecepatan aliran air di kran adalah 10 m/s tentukan:
a) Debit air
b) Waktu yang diperlukan untuk mengisi ember

2. Tangki air dengan lubang sedang bocor dan air mengalir. Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan:
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah

4. Sebuah pipa berbentuk “S” (seperti gambar), dialiri air. Luas penampang besar 10 cm² dan penampang kecil 5 cm². Apabila kecepatan aliran air pada pipa besar 2 m/s² dengan tekanan 40 kilopascal maka tekanan pada pipa kecil adalah …. (ρ_air = 10³ kg/m²)

5. Lihatlah gambar dibawah ini. Sebuah benda ketika dimasukkan ke dalam zat cair 1 terapung dengan ½ bagian volumenya berada di bawah permukaan dan ketika dimasukkan ke dalam zat cair 2 terapung ¾ bagian volumenya berada di bawah permukaan, maka perbandingan massa jenis zat cair 1 dan 2 adalah…

6. Sebuah pipa U diisi minyak dan air dan dalam keadaan stabil tampak seperti gambar. Bila perbedaan ketinggian (Δh) 4,8 cm, tinggi air 7,2 cm, dan massa jenis air 1.000 kg/m³ maka massa jenis minyak adalah…

7. Berapakah tekanan hidrostatis di dasar kolam dengan kedalaman air 2 m $(\rho_{air}=\text{ 1000 kg/m}^3,\text{g= 10 m/s}^2)$ .

8. Kapal selam berada pada kedalaman 50 m dibawah permukaan laut. Bila diketahui massa jenis air laut $\text{1,03 x 10}^3\text{kg/m}^3$ dan tekanan udara di atas permukaan laut $10^5$ Pa, berapa tekanan hidrostatis yang dialami kapal selam tsb. ( g = 10 m/s²)

9. Sebuah dongkrak hidroulik mempunyai dua penampang masing2 $A_1=10\text{ cm}^2$ dan $A_2=50\text{ cm}^2$ . Jika pada penampang A₁ diberi gaya F₁ = 10 N, berapakah berat beban maksimum yang dapat diangkat oleh penampang A₂?

10. Sepotong tembaga volumenya 20 cm³ dan massa jenisnya 9 gr/cm³, dimasukkan ke dalam air yang massa jenisnya 1 gr/cm³. Berapakah berat tembaga di dalam air? ( g= 9,800 cm/s²)

11. Sebuah jarum terapung di atas air, panjang jarum 5 cm dan memilki massa 5 gr. Tentukan tegangan permukaan air tersebut!

Rumus Fisika Lainnya

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

Rumus Mekanika Fluida Tekanan, Hidrostatis, Hukum Pascal, Apung, Navier-Stokes, Fluida Newton | Beserta Contoh-Contoh Soal dan Jawaban

Rumus Mekanika Fluida

Rumus Tekanan

Tekanan Hidrostatis

Tekanan mutlak dan tekanan gauge

Tekanan mutlak pada kedalaman zat cair

Hukum Pascal

Gaya Apung (Hukum Archimedes)

Mengapung, tenggelam, dan melayang

Persamaan Navier-Stokes

Fluida Newtonian vs. non-Newtonian

Persamaan pada fluida Newtonian

Hukum pendinginan Newton

Penurunan suhu dalam pendinginan Newton

Contoh Soal dan Jawaban dari Rumus Mekanika Fluida

1. Tony mengisi ember yang memiliki kapasitas 20 liter dengan air dari sebuah kran. Jika luas penampang kran dengan diameter D2 adalah 2 cm2 dan kecepatan aliran air di kran adalah 10 m/s tentukan: a) Debit air b) Waktu yang diperlukan untuk mengisi ember

2. Tangki air dengan lubang sedang bocor dan air mengalir. Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan: a) Kecepatan keluarnya air b) Jarak mendatar terjauh yang dicapai air c) Waktu yang diperlukan bocoran air untuk menyentuh tanah

4. Sebuah pipa berbentuk “S” (seperti gambar), dialiri air. Luas penampang besar 10 cm2 dan penampang kecil 5 cm2. Apabila kecepatan aliran air pada pipa besar 2 m/s2 dengan tekanan 40 kilopascal maka tekanan pada pipa kecil adalah …. (ρair = 103 kg/m2)

5. Lihatlah gambar dibawah ini. Sebuah benda ketika dimasukkan ke dalam zat cair 1 terapung dengan ½ bagian volumenya berada di bawah permukaan dan ketika dimasukkan ke dalam zat cair 2 terapung ¾ bagian volumenya berada di bawah permukaan, maka perbandingan massa jenis zat cair 1 dan 2 adalah…

6. Sebuah pipa U diisi minyak dan air dan dalam keadaan stabil tampak seperti gambar. Bila perbedaan ketinggian (Δh) 4,8 cm, tinggi air 7,2 cm, dan massa jenis air 1.000 kg/m3 maka massa jenis minyak adalah…

10. Sepotong tembaga volumenya 20 cm3 dan massa jenisnya 9 gr/cm3, dimasukkan ke dalam air yang massa jenisnya 1 gr/cm3. Berapakah berat tembaga di dalam air? ( g= 9,800 cm/s2)

11. Sebuah jarum terapung di atas air, panjang jarum 5 cm dan memilki massa 5 gr. Tentukan tegangan permukaan air tersebut!

Rumus Fisika Lainnya

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

1. Tony mengisi ember yang memiliki kapasitas 20 liter dengan air dari sebuah kran. Jika luas penampang kran dengan diameter D₂ adalah 2 cm² dan kecepatan aliran air di kran adalah 10 m/s tentukan:
a) Debit air
b) Waktu yang diperlukan untuk mengisi ember

2. Tangki air dengan lubang sedang bocor dan air mengalir. Jarak lubang ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 3,2 m. Tentukan:
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah

4. Sebuah pipa berbentuk “S” (seperti gambar), dialiri air. Luas penampang besar 10 cm² dan penampang kecil 5 cm². Apabila kecepatan aliran air pada pipa besar 2 m/s² dengan tekanan 40 kilopascal maka tekanan pada pipa kecil adalah …. (ρ_air = 10³ kg/m²)

6. Sebuah pipa U diisi minyak dan air dan dalam keadaan stabil tampak seperti gambar. Bila perbedaan ketinggian (Δh) 4,8 cm, tinggi air 7,2 cm, dan massa jenis air 1.000 kg/m³ maka massa jenis minyak adalah…

10. Sepotong tembaga volumenya 20 cm³ dan massa jenisnya 9 gr/cm³, dimasukkan ke dalam air yang massa jenisnya 1 gr/cm³. Berapakah berat tembaga di dalam air? ( g= 9,800 cm/s²)