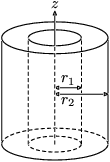
Rumus Momen inersia
Momen inersia adalah hasil kali partikel massa dengan kuadrat jarak tegak lurus partikel dari titik poros. Berikut adalah rumus momen inersia.
Satuan dari momen inersia adalah kg m² (Kilogram meter kuadrat).
Besaran momen inersia dari beberapa benda.
Hubungan antara torsi dengan momen inersia
Hukum II Newton tentang rotasi
Keterangan:
- I : momen inersia (kg m²)
- α : percepatan sudut (rad/s²)
: torsi (Nm)
Momen inersia (Satuan SI : kg m2) adalah ukuran kelembaman suatu benda untuk berotasi terhadap porosnya. Besaran ini adalah analog rotasi daripada massa. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalarterhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik.
Lambang 

Definisi skalar
Definisi sederhana momen inersia (terhadap sumbu rotasi tertentu) dari sembarang objek, baik massa titik atau struktur tiga dimensi, diberikan oleh rumus:
di mana m adalah massa dan r adalah jarak tegak lurus terhadap sumbu rotasi.
Analisis
Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh
Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik mi dengan jarak ri terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:
Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut:
di mana
- V adalah volume yang ditempati objek
- ρ adalah fungsi kerapatan spasial objek
- r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi) antara sumbu rotasi dan titik di benda tersebut.
Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk:
di mana
- M adalah massa
- R adalah jari-jari objek dari pusat massa (dalam beberapa kasus, panjang objek yang digunakan)
- k adalah konstanta tidak berdimensi yang dinamakan “konstanta inersia”, yang berbeda-beda tergantung pada objek terkait.
Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa dari pusat rotasi. Contoh:
- k = 1, cincin tipis atau silinder tipis di sekeliling pusat
- k = 2/5, bola pejal di sekitar pusat
- k = 1/2, silinder atau piringan pejal di sekitar pusat.
Hubungan antara torsi dengan momen inersia
Hukum II Newton tentang rotasi
Keterangan:
- I : momen inersia (kg m²)
- α : percepatan sudut (rad/s²)
: torsi (Nm)
Torsi
Torsi atau momen gaya adalah hasil kali antara gaya F dan lengan momennya. Torsi dilambangkan dengan lambang {\displaystyle \tau }
Satuan dari torsi adalah Nm (Newton meter).
Contoh Soal dan Jawaban Momen Inersia
1. Bola bermassa 100 gram dihubungkan dengan seutas tali yang panjangnya 30 cm seperti pada gambar. Momen inersia bola terhadap sumbu AB adalah…
2. Batang AB massanya 2 kg diputar melalui ujung A ternyata momen inersianya 8 kg.m2. Bila diputar melalui pusat O (AO = OB), momen inersianya menjadi….
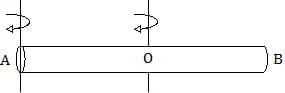
B. 4 kg.m2
C. 8 kg.m2
D. 12 kg.m2
E. 16 kg.m2
Pembahasan
Saat batang AB diputar dengan poros A, momen inersianya 8 kg.m2, sehingga panjang batang R dapat dicari dengan rumus:
I = mR2
8 = 2R2
R2 = 4
R = 2 m
Saat batang AB diputar dengan poros A, massa batang terbagi menjadi dua, demikian juga jarak terhadap poros:
mA = 1 kg
mB = 1 kg
RA = 1 m
RB = 1 m
Dengan demikian, momen inersianya menjadi:
I = ΣmR2
= mARA2 + mBRB2
= 1 × 12 + 1 × 12
= 1 + 1
= 2
Jadi, momen inersia pada keadaan tersebut adalah 2 kg.m2 (A).
3. Empat partikel masing-masing bermassa m, dihubungkan dengan batang ringan tak bermassa. Jika sistem partikel diputar dengan poros Y maka besar momen inersia sistem partikel adalah…
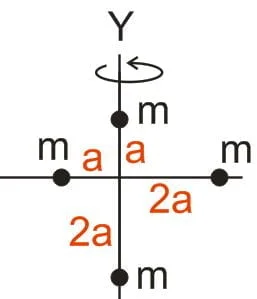
A. 3m.a2
B. 4m.a2
C. 5m.a2
D. 8m.a2
E. 15m.a2
Pembahasan:
Rumus momen inersia: ΣI=Σm⋅r2
Karena diputar terhadap sumbu Y, maka yang dihitung hanya partikel pada sumbu X saja.
ΣI=Σm⋅r²
= m1 R12 + m2R22
= m . a2 + m . (2a)2
= ma2 + 4ma2
= 5ma2
Jawaban : C
4. Tiga buah partikel dengan massa m, 2m, dan 3m dipasang pada ujung kerangka yang massanya diabaikan. Sistem terletak pada bidang xy. Jika sistem diputar terhadap sumbu y maka momen inersia sistem adalah….
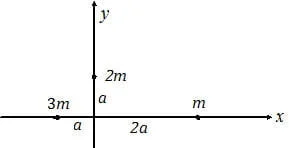
B. 7 ma
C. 5 ma2
D. 6 ma2
E. 7 ma2
Pembahasan
Karena sistem diputar terhadap sumbu y maka partikel yang bermassa 2m tidak berfungsi. Berarti hanya partikel yang berada pada sumbu x yang diperhitungkan. Anggap saja partikel di sebelah kiri berindeks (1) dan partikel sebelah kanan berindeks (2).
m1 = 3m
m2 = m
R1 = a
R2 = 2a
Momen inersia pada sistem tersebut adalah:
I = ΣmR2
= m1R12 + m2R22
= 3m × a2 + m × (2a)2
= 3ma2 + 4ma2
= 7ma2
Jadi, momen inersia sistem tersebut adalah 7 ma2 (E).

Rumus Fisika Lainnya
Fisika banyak diisi dengan persamaan dan rumus fisika yang berhubungan dengan gerakan sudut, mesin Carnot, cairan, gaya, momen inersia, gerak linier, gerak harmonik sederhana, termodinamika dan kerja dan energi. Klik disini untuk melihat rumus fisika lainnya (akan membuka layar baru, tanpa meninggalkan layar ini).
Bacaan Lainnya
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang
- Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender
- Cara Menghentikan Penindasan Bullying
- Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
- Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
- Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
- Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Apakah Produk Pembalut Wanita Aman?
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Physics, Tutor Vista
Isi Dari Bisnis Plan dan Contoh
Struktur tipikal untuk bisnis plan atau rencana bisnis untuk memulai usaha, sebaiknya Anda membuat bisnis plan, jika Anda ingin berhasil dalam kewirausahaan Anda. Berikut adalah 14 hal penting yang harus Anda tulis pada saat membuat Bisnis Plan:
1. Halaman sampul dan daftar isi
Cover page and table of contents atau halaman sampul dan daftar isi harus dibuat semenarik mungkin. Contohnya seperti sampul buku, jika menarik Anda ingin membaca isinya!

2. Ringkasan bisnis plan
Executive summary atau ringkasan bisnis plan merangkum laporan atau proposal yang lebih panjang atau sekelompok laporan terkait sedemikian rupa sehingga pembaca dapat dengan cepat berkenalan dengan sejumlah besar bahan tanpa harus membaca semuanya.
Biasanya berisi pernyataan singkat tentang masalah atau proposal yang tercakup dalam dokumen utama, informasi latar belakang, analisis ringkas dan kesimpulan utama. Ini dimaksudkan sebagai bantuan untuk pengambilan keputusan oleh manajer dan telah digambarkan sebagai bagian terpenting dari rencana bisnis.
Contoh executive summary dalam bisnis plan:
BUKA CAFÉ memiliki beragam unit bisnis di F&B, layanan katering, gerai kafe, internet, dan penjualan jejaring sosial.
Buka Café adalah konsep F&B baru dengan “Layanan Cepat” dan semi-restoran kasual yang menawarkan layanan take-out dan fitur menu makanan internasional, seperti Indonesia, Italia, Cina. Waktu penayangan biasanya dalam beberapa menit dan harga relatif murah. Makanan dapat dikonsumsi di luar lokasi, di rumah pelanggan atau lokasi kerja.
Kami akan menawarkan layanan katering penuh dan mudah, makanan yang dilayani oleh tempat makan dan minum biasanya dikonsumsi oleh pelanggan di tempat / oleh tempat mereka sendiri. Misalnya, perusahaan katering dapat menyiapkan dan menyajikan makanan untuk konvensi penjualan perusahaan di hotel, pesta, pertemuan kantor, dan banyak lagi.
Makanan kami unik dan eksklusif dan target konsumennya adalah wanita dan pria dengan pendapatan menengah ke bawah. Dengan fakta ini kami berharap dapat menarik lebih banyak orang yang menghargai variasi makanan.
Layanan luar kota dan penjualan internet / jaringan sosial terus mendukung semua unit bisnis. Saat ini, mereka adalah salah satu pemain terbaik dalam hal komunikasi dan penjualan.
Alasan dari rencana bisnis ini adalah untuk memastikan bahwa BUKA CAFÉ untuk mengekspresikan suatu tujuan sedemikian rupa sehingga mudah untuk melihat bagaimana hasilnya akan berdampak pada bottom line. Bisnis adalah tentang menghasilkan uang dan rencana bisnis dapat membantu memindahkan bisnis dari awal ke prospek menghasilkan uang, terutama untuk membantu kami dalam hal-hal berikut:
- Akan membantu meramalkan masa depan, bahkan jika masa depan tidak diketahui.
- Dapat membantu mengklarifikasi ceruk bisnis dan potensi pertumbuhan.
- Untuk membantu menyalurkan energi, uang, dan waktu ke arah yang terfokus, sehingga membantu memastikan kesuksesan.
- Sebagai alat untuk pengembangan dan pertumbuhan di masa depan.
Bagian ini tidak boleh diselesaikan sampai rencana bisnis ditulis. Ini akan menyoroti semua tonggak dalam pengembangan perusahaan selama lima tahun ke depan. Ini harus merangkum bidang-bidang berikut:
Tujuan rencana
Produk atau layanan dan kelebihannya
Peluang pasar
Tim manajemen
Lacak rekam, jika ada
Proyeksi keuangan
Persyaratan pendanaan
Proyeksi keuangan harus dirangkum dan “disorot”. Format berikut ini disarankan sebagai panduan:
| Tahun 1 | Tahun 2 | Tahun 3 | |
| Penjualan (Sales) | 1 886 250 000 | 2 357 812 500 | 2 947 265 625 |
| Penghasilan sebelum pajak (Net Profit before Tax) | 384 979 985 | 481 224 981 | 601 531 227 |
| Investasi | 279 590 048 | 209 692 536 | 157 269 402 |
| Ketenagakerjaan | 8 orang | 12 orang | 16 orang |
Untuk penjualan (sales): peningkatan 25% pada tahun ke-2 dan tahun ke-3.
Ingat bahwa calon investor sering membuat penilaian sementara berdasarkan ringkasan rencana bisnis atau ringkasan bisnis plan, dan bahwa keputusan mereka untuk membaca bagian utama dari rencana bisnis akan tergantung pada informasi yang disajikan di sini. Lampiran di bagian belakang rencana berisi informasi yang lebih rinci untuk mendukung teks utama dari rencana bisnis.
3. Pernyataan misi dan visi
Mission statement atau pernyataan misi adalah merupakan sebuah pernyataan yang digunakan sebagai cara untuk mengomunikasikan tujuan dari sebuah organisasi. Walaupun sering tidak berubah dalam jangka waktu yang lama, sebuah organisasi tidak lazim memperbarui pernyataan misi mereka dan umumnya terjadi ketika sebuah organisasi berkembang. Pernyataan misi biasanya ringkas dan pernyataan sederhana yang menunjukkan ikhtisar apa tujuan organisasi tersebut dan di sektor manakah organisasi tersebut bekerja.
Jangan hanya menulis misi dan visi, tetapi Anda juga harus dapat melakukannya!
Contoh visi dan misi:
Visi: menjadi café di area yang dapat dijangkau semua kalangan.
Misi: mempekerjakan dan membeli bahan dasar makanan yang tidak jauh dari tempat café, agar bumi menjadi lebih hijau!
Misi
Buka Café akan menggunakan teknologi untuk mengidentifikasi dan melayani target audiens yang ideal dalam radius 30 km dari tempat tersebut. Perusahaan akan menggunakan teknik pemasaran canggih untuk mengamankan klien inti dari pengusaha eksekutif dan akun korporat.
Buka Café berdedikasi untuk beroperasi dengan antusiasme yang konstan untuk belajar, terbuka untuk mengimplementasikan ide-ide baru dan memelihara kemauan untuk beradaptasi dengan kondisi pasar yang berkembang.
Kunci Sukses
• Menggunakan teknologi untuk mengembangkan klien laki-laki yang loyal dan sering membeli, alih-alih pembeli eceran makanan tradisional.
• Merancang dan menjual F&B berkualitas inovatif dan bernilai uang dengan menggunakan berbagai gaya, bumbu, dan wadah makanan desain.
• Membuat etalase yang menyerupai galeri seni, dengan F&B segar yang ditampilkan seperti seni (dan selalu dijual).
• Menawarkan produk tambahan, termasuk cokelat gourmet dan karya seni asli dari seniman lokal.
• Berkomunikasi dengan pelanggan potensial melalui surat langsung, iklan cetak, dan situs web yang mudah digunakan.
• Menawarkan acara di dalam toko gratis, seperti penandatanganan buku dan pertunjukan seni, yang bertepatan dengan pembukaan galeri lingkungan lainnya.
4. Deskripsi bisnis
Jelaskan dengan tepat bisnis Anda.
Pemegang Saham
Buka Café, adalah salah satu makanan semi-cepat baru di Indonesia, telah mengembangkan reputasinya untuk yang baru dan inovatif, menggabungkan layanan cepat & nilai uang yang baik, dengan standar layanan pelanggan yang sangat baik.
Kepemilikan Perusahaan
Nama pemegang saham dan investasi tunai hingga saat ini:
- Bapak Jonathan memiliki saham 50%.
- Ibu Rini memiliki 25% saham.
- Bapak Michael memiliki 25% saham.
- Ibu Candra memiliki 25% saham.
Bapak Jonathan adalah CEO kami, berpengalaman dalam industri layanan makanan & penginapan. Dia dididik di Jakarta & Singapura terutama di industri bisnis. Dia membawa pengetahuan dan keahlian yang luas ke perusahaan.
Ibu Rini adalah General Manager kami dan latar belakang pendidikannya di Australia. Dia memainkan peran utama dalam pengembangan program yang meningkatkan produktivitas dan kualitas. Dia memastikan bahwa grup beroperasi dengan lancar dan mencapai keunggulan dalam kinerja operasional, profitabilitas, efisiensi serta secara efektif mencapai tujuan dan sasaran bisnis.
Bapak Michael adalah Direktur Keuangan kami yang berbasis di Australia dan mengelola beberapa perusahaan.
Dia dipercaya untuk mengawasi perencanaan keuangan grup, sistem kontrol internal, manajemen kas dan bank, audit dan pajak serta manajemen keuangan perusahaan secara keseluruhan. Selain itu juga bertanggung jawab dalam persiapan perencanaan anggaran dan proses pengembangan untuk kelompok.
Sistem pelaporannya yang unggul mencakup laporan keuangan terintegrasi dari semua merek portofolio dan alat keputusan bisnis informasi yang membantu operasi dalam mendorong margin laba yang lebih tinggi. Dia menguasai bidang yang sangat khusus termasuk pengembangan proyek, manajemen operasi waralaba, pengembangan dan konsultasi strategis, evaluasi keuangan, layanan dukungan pemilik, penilaian dan analisis akuisisi.
Direktur Penjualan & Pemasaran kami (dipantau jarak jauh), dipimpin oleh Ibu Candra yang berbasis di Bali. Dia dibantu oleh tim yang sangat berpengalaman dan personel pengembangan bisnis yang berdedikasi yang berbasis di Paris.
Divisi ini bertanggung jawab untuk pertumbuhan dan pengembangan serta implementasi strategi bisnis dari masing-masing unit bisnis sesuai dengan rencana bisnis perusahaan. Direktur secara konstan meninjau dan menganalisis tren bisnis saat ini dan dia memastikan bahwa grup tersebut mencapai sasaran kuantifikasi yang diinginkan.
Produk dan layanan
<< Jelaskan dengan jelas apa produk atau layanan Anda dan apa fungsinya. Produk-produk ini menyediakan konsumen dengan berbagai macam lini produk dan memungkinkan untuk kustomisasi pesanan individu. >>
• Latar belakang perkembangannya.
BUKA CAFÉ OFFICE lahir untuk memastikan kelanjutan dan perluasan luas bisnis bunga.
• Manfaat dan Fitur.
Layanan cepat & nilai uang yang baik adalah situasi yang saling menguntungkan bagi kedua belah pihak.
• Nilai jual yang unik.
Bebas repot dan pengalaman membeli makanan dan minuman. Menu Harian berubah setiap hari, dari Jawa ke Sumatera, melalui favorit Singapura atau Malaysia. Mereka dapat mencoba makanan Italia jika bosan, sandwich dan hot dog jika mereka mau. Buka Café memiliki produk varietas dan ini adalah jaminan klien kami.
• Keuntungan bagi pelanggan.
Hemat waktu & uang. Untuk pesanan yang lebih dibuat khusus dan canggih, klien akan memiliki lebih banyak pilihan dalam membuat makanan mereka puas.
• Kekurangan atau titik lemah.
Dikenal karena makanan berkalori tinggi dan makanan berkualitas lebih rendah untuk orang-orang tertentu, tetapi makanan kita akan lebih sehat daripada yang mereka kira dan kita mengadopsi model bisnis makanan sehat. Kami melayani sandwich ayam panggang, membungkus, atau salad untuk mengkompensasi atau permintaan khusus (jika ada).
• Gerai pengembangan masa depan:
belum ditentukan.
Unit Bisnis BUKA CAFÉ
- Buka Café
Menjual makanan dan minuman jenis: Amerika, Eropa dan Asia.
- Take-away corner cepat saji Buka café
Dengan kesibukan yang berbeda-beda, corner Buka Café akan melayani take-away dengan loket tersendiri.
- Penjualan internet
Dengan adanya Go-Jek, kami harus selalu meng-update apa saja yang harus dijual di platform Go-Jek.
Produk
• Desain Makanan Asli, Menggunakan Berbagai pilihan daun & buah hiasan. Setiap pengaturan makanan Buka Café akan menjadi karya seni yang alami, asli, dan jenisnya.
• Wadah Unik.
Buka Café akan mengembangkan dan membeli (yang sudah tersedia di pasaran) kemasan khusus untuk menjaga agar wadah tetap tegak dan tidak tumpah. Kemasan ini akan dicap dengan baik dengan logo perusahaan dan akan berfungsi sebagai kendaraan pemasaran tambahan setelah dikirimkan ke tempat kerja pelanggan (gedung kantor).
Akan memilih dan menawarkan piring & gelas kertas-plastik yang khas untuk pembeli bebas atau untuk acara khusus (katering, Ramadhan / Idul Fitri, Tahun Baru, serta pilihan yang terjangkau untuk pembelian rutin.
• Cokelat Gourmet. Dengan meningkatnya kesadaran konsumen akan merek cokelat dan kemauan untuk membayar untuk produk yang lebih baik untuk acara-acara khusus, Buka Café akan membawa 1 atau 2 baris cokelat gourmet dengan harga terjangkau, yaitu, merek tidak akan dijual oleh pengecer / supermarket lain. . Penjualan coklat gourmet adalah pelengkap sempurna untuk makanan dan mendorong konsumen untuk menikmati dan mengalami sesuatu yang baru karena mereka layak.
• Jasa katering. Berbagai harga terjangkau. Buka Café akan menawarkan berbagai ukuran makanan dan akan selalu membuat pengaturan unik untuk memenuhi anggaran yang dinyatakan oleh siapa pun.
• Lukisan dan Karya Seni dari Artis Lokal. Untuk membuat lingkungan galeri, toko Buka Café akan menampilkan lukisan dan / atau gambar dari seniman lokal dan karya seni akan dijual. Perusahaan akan mengumpulkan persentase kecil dari setiap penjualan (5%).
• Makanan anak-anak.
Dengan design, gambar dan penataan yang unik, akan selalu mengundang gairah makan anal-anak.
Layanan lainnya
Dalam bisnis plan ini, Buka Café akan membuat Buka Café Club. Acara-acara khusus mencakup empat dari setiap sepuluh pembelian makanan yang dilakukan. Untuk menangkap sebagian dari pasar ini dan untuk menumbuhkan nafsu makan secara keseluruhan, Buka Café akan menawarkan Frequent Food Gift Program yang disebut Forget-Me-Not Club yang dirancang untuk klien. Program ini akan memungkinkan setiap pelanggan mendaftar minimal enam hari per tahun (ulang tahun, liburan, peringatan atau hari apa pun kecuali Hari Valentine) di mana Buka Café akan secara otomatis berencana untuk mengirimkan pesan / email.
Program Akun Komersial termasuk:
• Konsultasi awal gratis. Untuk penyewaan tempat event, sekolah, dan kantor yang tertarik dengan program pengiriman harian, Buka Café akan melakukan kunjungan awal gratis di tempat ke kantor atau toko pelanggan untuk menentukan rencana makanan yang optimal.
• Program pengiriman prioritas. Buka Café akan bekerja dengan setiap pelanggan komersial untuk menentukan jadwal pengiriman mingguan dan akan memastikan bahwa makanan dikirim pada hari yang sama setiap minggu pada waktu yang sama.
• Makanan Ulang Tahun / Kue. Buka Café akan menawarkan pengaturan gratis kepada setiap manajer kantor untuk akun komersial pada hari ulang tahunnya.
• Program “menggaet atau klien membawa klien baru”. Buka Café akan menawarkan diskon 25% satu kali untuk setiap pelanggan komersial untuk setiap kalinya membawa klien baru yang menjadi pelanggan.
Sumber bahan makanan
Sumber bahan makanan segar akan dikirimkan setiap minggu oleh distributor kami langsung dari kota “ini”. Kami juga memiliki perjanjian dengan Perusahaan Q untuk secara eksklusif memproduksi saus khas kami, dan semua barang dagangan kami akan dicetak dan diproduksi oleh kantor mitra kami di Cina.
5. Analisis lingkungan bisnis
Bagaimana lingkungan bisnis Anda? Dalam bisnis plan, Anda perlu mengidentifikasi banyak faktor.
Ketika Anda memulai atau menjalankan bisnis, Anda harus dapat mengidentifikasi kekuatan dan kelemahan bisnis dengan informasi pasar dan dengan menilai faktor internal dan eksternal. Seorang manajer perlu memahami bagaimana faktor lingkungan dapat memengaruhi dan memengaruhi bisnis.
Analisis PESTLE, yang kadang-kadang disebut analisis PEST, adalah konsep dalam prinsip pemasaran. Selain itu, konsep ini digunakan sebagai alat oleh perusahaan untuk melacak lingkungan tempat mereka beroperasi atau berencana untuk meluncurkan proyek / produk / layanan baru, dll.
PESTLE adalah singkatan dari;
- P untuk Politik.
- E untuk Ekonomi.
- S untuk Sosial.
- T untuk Teknologi.
- L (Law) untuk Hukum.
- E (Environment) untuk Lingkungan.
Sangat penting bagi seseorang untuk memahami kedalaman lengkap dari masing-masing huruf PESTLE. Seperti di bawah ini:
Politik
Faktor-faktor ini menentukan sejauh mana pemerintah dapat mempengaruhi ekonomi atau industri tertentu. Misalnya, pemerintah dapat mengenakan pajak atau bea baru yang dengannya seluruh struktur organisasi yang menghasilkan pendapatan dapat berubah. Faktor-faktor politik termasuk kebijakan pajak, kebijakan fiskal, tarif perdagangan, dll.
Yang dapat dipungut pemerintah sekitar tahun fiskal dan dapat mempengaruhi lingkungan bisnis (lingkungan ekonomi) secara luas.
Faktor-faktor yang pada dasarnya adalah bagaimana campur tangan pemerintah dalam perekonomian.
Secara khusus, faktor-faktor politik termasuk: kebijakan pajak, hukum perburuhan, hukum lingkungan, pembatasan perdagangan, tarif, dan stabilitas politik. Faktor-faktor politik juga dapat mencakup barang-barang dan jasa yang akan diberikan atau diberi oleh pemerintah serta berbagai hal yang tidak ingin disediakan oleh pemerintah.
Lebih jauh, pemerintah memiliki dampak yang tinggi pada kesehatan, pendidikan, dan infrastruktur pada negara.
Ekonomi
Faktor-faktor ini merupakan penentu kinerja ekonomi yang secara langsung berdampak pada perusahaan dan memiliki efek jangka panjang yang menggema. Misalnya, kenaikan tingkat inflasi ekonomi apa pun akan memengaruhi cara perusahaan menghargai produk dan layanan mereka.
Selain itu, itu akan mempengaruhi daya beli konsumen dan mengubah model permintaan / penawaran untuk ekonomi itu. Faktor ekonomi termasuk tingkat inflasi, suku bunga, nilai tukar mata uang asing, pola pertumbuhan ekonomi, dll. Ini juga memperhitungkan investasi langsung asing, tergantung pada industri tertentu yang menjalani analisis ini.
Faktor yang termasuk dalam aspek ini seperti: pertumbuhan ekonomi, suku bunga, nilai tukar, tingkat inflasi. Faktor-faktor ini sangat mempengaruhi bagaimana bisnis beroperasi dan membuat keputusan. Misalnya, suku bunga mempengaruhi biaya modal perusahaan dan dari situ sejauh mana perusahaan tersebut dapat tumbuh dan berkembang.
Nilai tukar dapat mempengaruhi biaya dari barang-barang ekspor dan pasokan dan harga barang-barang impor dalam perekonomian. Baca juga? Hiperinflasi – Definisi, Penyebab, Efek, Cara Mengatasi dan Contoh
Sosial
Faktor-faktor ini meneliti lingkungan sosial pasar, dan mengukur faktor-faktor penentu seperti tren budaya, demografi, analisis populasi, dll. Contoh untuk ini dapat berupa tren pembelian untuk negara-negara Barat seperti AS di mana terdapat permintaan tinggi selama musim liburan.
Teknologi: Faktor-faktor ini berkaitan dengan inovasi dalam teknologi yang dapat mempengaruhi operasi industri dan pasar secara menguntungkan atau tidak menguntungkan. Ini mengacu pada otomatisasi, penelitian dan pengembangan dan jumlah kesadaran teknologi yang dimiliki pasar.
Law (Hukum)
Faktor-faktor ini memiliki sisi eksternal dan internal. Ada undang-undang tertentu yang memengaruhi lingkungan bisnis di negara tertentu sementara ada kebijakan tertentu yang dipelihara perusahaan untuk diri mereka sendiri. Analisis hukum memperhitungkan kedua sudut ini dan kemudian memetakan strategi berdasarkan undang-undang ini. Misalnya, hukum konsumen, standar keselamatan, hukum perburuhan, dll. Baca juga ? Hukum di Indonesia – Pengertian dan Contoh
Environment (Lingkungan)
Faktor-faktor ini mencakup semua yang mempengaruhi atau ditentukan oleh lingkungan sekitarnya. Aspek PESTLE ini sangat penting untuk industri tertentu khususnya misalnya pariwisata, pertanian, pertanian, dll. Faktor-faktor analisis lingkungan bisnis mencakup tetapi tidak terbatas pada iklim, cuaca, lokasi geografis, perubahan global dalam iklim, penyeimbang lingkungan, dll.
6. Analisis SWOT
Analisis SWOT adalah metode perencanaan strategis yang digunakan untuk mengevaluasi dalam dunia bisnis: kekuatan (strengths), kelemahan (weaknesses), peluang (opportunities), dan ancaman (threats) dalam suatu proyek atau suatu spekulasi bisnis.
Berikut ini contoh analisis SWOT untuk bisnis kemeja dan kaos online yang disesuaikan. Meskipun lebih banyak faktor muncul selama brainsorming, ini dianggap yang paling penting.
Strengths (kekuatan)
| Weaknesses (kelemahan)
|
Opportunities (peluang)
| Threats (ancaman)
|
Pikirkan tentang strategi apa yang dapat diterapkan oleh pemilik bisnis ini untuk memanfaatkan informasi ini. Ingat, tidak ada jawaban yang benar atau salah di sini.
7. Latar belakang industri
Industry background atau latar belakang industri mencatat secara keseluruhan tentang industri dalam bisnis plan.
Dikutip dari Indonesia Investment, Jika kita melihat lebih dekat, maka kita melihat bahwa Kementerian Perindustrian Indonesia menetapkan target investasi IDR 53,18 triliun (sekitar USD $ 3,9 miliar) untuk industri makanan nasional dan target investasi IDR 10,07 triliun (sekitar USD $ 735 juta) untuk industri minuman.
Oleh karena itu, total investasi langsung dalam industri makanan dan minuman Indonesia ditargetkan mencapai 63,25 triliun pada tahun penuh 2018.
Posisi kami di Industri
West Vancouver adalah daerah makmur dengan kepadatan hewan peliharaan yang tinggi, pasar yang ideal untuk bisnis hewan peliharaan seperti Nenek Pet. Orang-orang di daerah ini tidak hanya memiliki hewan peliharaan, tetapi mampu mengeluarkan uang untuk mereka dan bersedia melakukannya.
Riset pasar
Riset pasar kami telah menunjukkan bahwa sembilan dari 10 pemilik hewan peliharaan yang disurvei di Vancouver Barat akan lebih memilih untuk memelihara hewan peliharaan mereka di rumah mereka sendiri ketika mereka bepergian daripada dikuduskan dan enam dari 10 akan mempertimbangkan memiliki pengasuh hewan peliharaan yang menyediakan perusahaan anjing ketika mereka sedang bekerja.
8. Analisis pesaing
Competitor analysis atau analisis dalam pemasaran dan manajemen strategis adalah penilaian kekuatan dan kelemahan pesaing saat ini dan yang potensial. Analisis ini memberikan konteks strategis ofensif dan defensif untuk mengidentifikasi peluang dan ancaman. Profiling menggabungkan semua sumber analisis pesaing yang relevan ke dalam satu kerangka kerja dalam mendukung perumusan strategi, implementasi, pemantauan, dan penyesuaian strategi yang efisien dan efektif. Selanjutnya baca ? Analisis Pesaing – Competitor Analysis dalam Bisnis dan Contohnya – Cara Melakukan Analisis Pesaing atau Analisis Kompetitif
- Tentukan industri – ruang lingkup dan sifat industri.
- Tentukan siapa kompetitornya.
- Tentukan siapa pelanggan dan manfaat apa yang mereka harapkan.
- Tentukan kekuatan utama – misalnya harga, layanan, kenyamanan, inventaris, dll.
- Rangking faktor-faktor kunci keberhasilan dengan memberikan bobot kepada masing-masing – Jumlah dari semua bobot harus dijumlahkan menjadi satu.
- Nilai setiap pesaing pada masing-masing faktor kunci keberhasilan.
- Lipat gandakan setiap sel dalam matriks dengan faktor pembobotan.
Contoh Pesaing:
- Pizza express: 200 meter. Harga rata-rata Rp 60 000.
- Cafe ABC: 350 meter. harga rata-rata Rp 55 000.
- Rumah makan Indonesia: 500 meter. Harga rata-rata Rp 45 000.
9. Analisis Pasar
Market analysis atau analisis pasar mempelajari daya tarik dan dinamika pasar khusus dalam industri khusus. Ini adalah bagian dari analisis industri dan dengan demikian pada gilirannya analisis lingkungan global. Melalui semua analisis ini, kekuatan, kelemahan, peluang dan ancaman (SWOT) perusahaan dapat diidentifikasi. Akhirnya, dengan bantuan analisis SWOT, strategi bisnis yang memadai dari sebuah perusahaan akan ditentukan.
Analisis pasar juga dikenal sebagai investigasi terdokumentasi tentang pasar yang digunakan untuk menginformasikan kegiatan perencanaan perusahaan, khususnya seputar keputusan inventaris, pembelian, perluasan / kontraksi tenaga kerja, perluasan fasilitas, pembelian peralatan modal, kegiatan promosi, dan banyak aspek lain dari suatu perusahaan.
Dimensi analisis pasar
David A. Aaker menguraikan dimensi berikut dari analisis pasar:
Ukuran pasar (saat ini dan masa depan).
Trend pasar.
Tingkat pertumbuhan pasar.
Profitabilitas pasar.
Struktur biaya industri.
Saluran distribusi.
Faktor kunci keberhasilan.
Detail kunci keberhasilan.
<< Bagian ini mencakup riset pasar dan analisis pesaing. Anda harus menunjukkan bahwa Anda telah melakukan riset pasar untuk membenarkan proyeksi yang dibuat dalam rencana bisnis Anda. Itu harus menunjukkan bahwa ada pasar yang layak dan bahwa Anda dapat mengalahkan persaingan di pasar untuk penjualan. >>
Saat ini, pasar untuk produk bunga permanen berkembang pesat. Menurut statistik tahun 1993, nilai produk bunga permanen untuk tahun fiskal 1992 adalah lebih dari $ 2,2 miliar, dan masih terus tumbuh.
Industri hadiah juga meningkat, karena rumah tangga yang dikepalai oleh 45 hingga 54 tahun adalah pembeli hadiah terbesar.
Sasaran pasar
<< Pasar tempat Anda berencana menjual produk atau layanan. Analisis segmen pasar ini sebagai berikut:
• Ukuran setiap segmen pasar
• Apakah segmen tumbuh atau menurun?
• Karakteristik pelanggan potensial di setiap segmen >>
10. Rencana pemasaran
Bagaimana Anda akan memasarkan bisnis Anda? Rencana pemasaran usaha Anda dalam bisnis plan merupakan hal yang penting.
Marketing plan atau rencana pemasaran dapat menjadi bagian dari keseluruhan rencana bisnis. Strategi pemasaran yang solid adalah dasar dari rencana pemasaran yang ditulis dengan baik. Sementara rencana pemasaran berisi daftar tindakan, tanpa landasan strategis yang sehat, itu tidak banyak berguna untuk bisnis.
Tujuan pemasaran biasanya harus didasarkan, terutama, pada tujuan keuangan organisasi; mengubah pengukuran keuangan ini menjadi pengukuran pemasaran terkait. Dia kemudian menjelaskan pandangannya tentang peran “kebijakan,” dengan strategi yang paling sering membingungkan: “Kebijakan adalah aturan atau pedoman yang menyatakan ‘batas’ di mana tindakan harus terjadi.” Menyederhanakan, strategi pemasaran dapat dilihat sebagai sarana, atau “rencana permainan,” di mana tujuan pemasaran akan dicapai dan, dalam kerangka kerja yang muncul di sini, umumnya berkaitan dengan 8 P. Contohnya adalah:
Price (Harga) – Jumlah uang yang dibutuhkan untuk membeli produk
Product (Produk) – Produk aktual
Promotion (Promosi atau iklan) – Mengenal produk
Placement (Penempatan) – Tempat produk dijual
People (Orang) – Mewakili bisnis
Physical environment (Lingkungan fisik) – Suasana, suasana hati, atau nada lingkungan
Process (Proses) – Layanan bernilai tambah yang membedakan produk dari pesaing (mis. Layanan purna jual, jaminan)
Packaging (Pengemasan) – Bagaimana produk akan dikemas dan dilindungi
Isi atau Konten Rencana Pemasaran
Rencana Pemasaran untuk bisnis kecil biasanya mencakup Small Business Administration Deskripsi pesaing, termasuk tingkat permintaan untuk produk atau layanan dan kekuatan dan kelemahan pesaing
Deskripsi produk atau layanan, termasuk fitur-fitur khusus.
Anggaran pemasaran, termasuk rencana iklan dan promosi.
Deskripsi lokasi bisnis, termasuk kelebihan dan kekurangan untuk pemasaran.
Strategi penetapan harga.
Segmentasi pasar.
<< Bagian ini menetapkan strategi Anda untuk mencapai target pasar Anda, membangkitkan minat mereka pada produk atau layanan Anda, dan benar-benar memberikan produk atau layanan kepada mereka dalam penjualan. >>
Ada banyak restoran dan warung semi-cepat di pusat kota.
Sebuah restoran makanan semi-cepat dengan bisnis niche yang jelas dapat berkembang. Strategi pemasaran Buka Café adalah mengembangkan bisnis niche khusus dan independen yang berpusat di sekitar Frequent Food Gift Programs dan menghadirkan produk-produk berkualitas, bernilai baik untuk uang dan layanan katering pelanggan pribadi yang istimewa.
BUKA CAFÉ berfokus pada penyediaan produk berkualitas dengan nilai terbaik untuk uang kepada konsumen dengan layanan luar biasa. Kustomisasi pesanan dan spesialisasi layanan akan menciptakan keunggulan kompetitif.
BUKA CAFÉ mengembangkan organisasi dengan memulainya dengan sedikit karyawan untuk mengurangi biaya. Semua karyawan saat ini termotivasi, menghasilkan budaya perusahaan yang positif dan kuat. Budaya ini akan dibawa ke semua peserta pelatihan baru, yang merupakan tujuan utama untuk perluasan KANTOR BUKA CAFÉ di setiap unit bisnis yang ada dan yang baru.
Tahun pertama layanan akan menjadi yang paling penting, karena BUKA CAFÉ berencana untuk membangun hubungan yang kuat dengan pemasok dan pembeli. Hubungan ini akan membantu BUKA CAFÉ OFFICE untuk tumbuh dan berkembang di industri ini.
Strategi Pemasaran
<< Bagaimana Anda akan memposisikan produk atau layanan Anda di pasar dan membedakannya dari para pesaingnya:
- Segmen pasar mana yang akan menjadi target pertama dan mengapa?
- Demografi
- Usia: 15 – 40
- Jenis Kelamin: Laki-laki & perempuan
- Status pernikahan: menikah & belum menikah
- Pekerjaan: pekerja kantor pusat kota, mulai dari pangkat & file dan siswa
- Pendidikan: nonpendidikan
- Demografi
- Geografis
- Pusat: Perkantoran
- Perusahaan
- Hotel dengan atau tanpa restoran
- Sekolah / universitas
- Bagaimana ini akan dikembangkan untuk mencapai target pasar penuh?
Pemasaran online & offline yang agresif
- Bagaimana Anda membedakan produk atau layanan Anda?
Cepat, presentasi bagus / gaya, enak dan terjangkau.
- Apa manfaat utama yang akan ditonjolkan?
Keramah tamahan staf, penyajian cepat dan tatanan bagus.
- Pelanggan potensial apa yang sudah Anda targetkan?
Pekerja / staf kantor, mahasiswa
- Sudahkah Anda memiliki lokasi pengujian dalam operasi dan umpan balik (feedback) apa yang berasal dari ini?
Di rumah nenek, dengan mengungang tetangga sekitar 35 orang. Feedback beragam, beberapa makanan terlalu asin, manis, pedas. Beberapa minuman terlalu manis dan asam. Feedback ini sangat bagus, karena kita harus berhati-hati agar makanan / minuman memiliki rasaya yang pas untuk hampir setiap orang. Lama penyajian berkisar dari 10-25 menit. yang 25 menit terlalu lama, jadi harus berhati-hati.
- Kontak apa yang dapat digunakan untuk menghasilkan kesadaran pasar dan penjualan?
Pemasaran Internet, publikasi radio, kunjungan kantor & universitas.
- Siapa yang akan melakukan pemasaran:
- Ibu Candra untuk mengoordinasikan iklan online & offline.
- Staf (dengan layanan yang baik dan cepat + senyum).
- Agensi online seperti: Google, Instagram, Facebook, dll.
Strategi penjualan
<< Bagaimana Anda akan menjual produk atau layanan Anda ke target pasar.
- Langsung.
- Eceran.
- Distributor.
- Agen.
- Situs web.
- Jejaring sosial: Facebook, Twitter, Pinterest, dll.
- Mitra Bagi Hasil / penyedia bisnis.
Harga
<< Bagaimana Anda akan menetapkan harga yang dikenakan untuk produk atau layanan Anda. Pertimbangan meliputi:
- Harga pesaing.
- Tingkat persaingan di pasar.
- Persepsi hubungan kualitas-harga oleh pelanggan.
- Biaya produksi dan biaya overhead.
- Rantai distribusi dan nilai tambah pada setiap tahap.
- Sejauh mana pembeli dapat mengendalikan harga.
Nyatakan bagaimana setiap produk atau layanan akan diberi harga, mengacu pada sumber pendapatan di atas. >>
- Nasi putih: Rp 3 000.
- Sate ayam 10 tusuk: Rp 10 000.
- Sate daging 10 tusuk: Rp 15 000.
- 4 Sosis ayam (panjang 15 cm masing-masing): Rp 7 500.
- 4 Sosis daging (panjang 15 cm masing-masing): Rp 11 500.
- Es teh manis: Rp 2 500.
11. Perencanaan operasional
Operational plan atau perencanaan operasional adalah proses perencanaan sasaran dan sasaran strategis untuk sasaran dan sasaran taktis. Ini menggambarkan tonggak sejarah, kondisi untuk keberhasilan dan menjelaskan bagaimana, atau bagian apa dari, rencana strategis akan dioperasikan selama periode operasional tertentu, dalam kasus aplikasi komersial, tahun fiskal atau periode anggaran tertentu lainnya.
Rencana operasional adalah dasar untuk, dan pembenaran atas permintaan anggaran operasional tahunan. Oleh karena itu, rencana strategis lima tahun biasanya akan membutuhkan lima rencana operasional yang didanai oleh lima anggaran operasional.
Rencana operasional harus menetapkan kegiatan dan anggaran untuk setiap bagian dari organisasi untuk 1 – 3 tahun ke depan. Mereka mengaitkan rencana strategis dengan kegiatan yang akan diberikan organisasi dan sumber daya yang diperlukan untuk mewujudkannya.
Rencana operasional harus memuat
Tujuan yang jelas dari mereka.
Kegiatan yang akan disampaikan.
Standar kualitas.
Hasil yang diinginkan.
Persyaratan kepegawaian dan sumber daya.
Jadwal implementasi.
Sebuah proses untuk memantau kemajuan.
Apa rencana operasional perusahaan Anda? Jawab pertanyaan ini!
Sebuah rencana operasional diambil langsung dari rencana strategis perusahaan Anda untuk menggambarkan misi, visi, sasaran, program dan kegiatan program. Seperti rencana strategis, rencana operasional menjawab 4 pertanyaan Anda:
Dimana kita sekarang?
Di mana kita ingin berada?
Bagaimana kita bisa sampai di sana?
Bagaimana kita mengukur kemajuan kita?
Operasi Toko
BUKA CAFÉ akan dibuka untuk beroperasi Senin – Minggu.
Shopping Mall ABC Outlet jam operasi: 10:00 pagi – 10:00 malam Senin minggu.
Jam dapat diperpanjang selama liburan dan / atau sesuai dengan masing-masing jam outlet membuka & menutup di setiap pusat perbelanjaan.
Kebijakan Toko
Perusahaan akan membangun kebijakan untuk membangun kepercayaan dengan pelanggan dan untuk mempertahankan retensi dan loyalitas.
Perusahaan akan berinvestasi dalam perangkat lunak manajemen hubungan pelanggan (CRM) dan sistem point of sales (POS) sederhana untuk melacak penjualan dan mengumpulkan informasi pelanggan, termasuk nama, alamat, alamat email dan informasi terkait lainnya (hewan peliharaan, suka / tidak suka bunga, preferensi warna, alergi, ulang tahun, ulang tahun). Informasi ini akan digunakan dengan upaya email dan direct mail untuk membangun program pemasaran khusus, membangun loyalitas pelanggan dan mendorong pendapatan.
Tujuan Jangka Panjang Bisnis
Tujuan jangka panjang bisnis kami untuk diakui dan nilai yang baik untuk merek uang di Indonesia dan luar negeri melalui, akuisisi, usaha patungan, pembagian keuntungan, kemitraan pemasaran aliansi strategis dan investasi organik.
Tujuan
Selama 5 tahun ke depan kita harus mampu meningkatkan penjualan, pengembangan, pengembangan, dan menstabilkan lapangan kerja.
1. Pada tahun pertama, kami akan memperluas ke katalog surat langsung dan belanja internet.
2. Pada Tahun pertama, kedua dan ketiga, kami akan mencoba mempertahankan margin kotor 25 persen.
3. Perbanyak keluarga produk dengan menambahkan 10 jenis bunga dan rangkaian bunga utama pada tahun 2014, yaitu: papan bunga setengah jadi, pengaturan standar.
4. Membangun program penetapan harga berdasarkan asumsi laba 10%.
* Catatan: BUKA CAFÉ OFFICE akan dibuka per 1 Januari, di Tahun Pertama. Peningkatan persentase yang besar di Tahun Dua mencerminkan pendapatan 12 bulan penuh (dibandingkan 10 bulan di Tahun Satu), manfaat pemasaran satu tahun, dan dimasukkannya Hari Valentine dan Paskah / Paskah. Hari Valentine saja biasanya menyumbang sepertiga dari pendapatan tahunan toko bunga.
12. Ringkasan manajemen
Management summary atau ringkasan manajemen menjelaskan bagaimana bisnis Anda terstruktur, memperkenalkan siapa yang terlibat, menguraikan sumber daya eksternal dan menjelaskan bagaimana bisnis dikelola.
Bagian ini mencadangkan semua data yang Anda sertakan di tempat lain dalam rencana bisnis dengan menunjukkan keahlian tim dan sumber daya di belakang perusahaan Anda.
Struktur Bisnis: Struktur bisnis apa yang akan diambil perusahaan Anda, kepemilikan perseorangan, LLC, kemitraan atau korporasi? Penentuan ini akan menjadi dasar untuk sisa area di bagian ini.
Tim Manajemen: Siapa yang akan mengawasi perusahaan? Jika Anda membentuk korporasi, siapa yang akan menjadi Dewan Direksi? Bagan organisasi dapat menjadi visual yang baik untuk menggambarkan elemen ini.
Kesenjangan Tim Manajemen: Apa yang dibutuhkan oleh personel Anda? Bagaimana setiap peran, setelah diisi, akan berkontribusi pada keberhasilan perusahaan Anda?
Personil Lainnya: Selain Dewan dan karyawan Anda, dukungan eksternal apa yang akan membantu fungsi bisnis? Ini dapat mencakup pengacara, akuntan, profesional hubungan masyarakat, dukungan administratif dan bahkan dewan penasihat eksternal.
Rencana Pertumbuhan Personil: Berapa gaji setiap orang untuk terlibat dengan perusahaan selama tiga tahun ke depan? Ini harus menyediakan biaya garis bawah untuk pengeluaran pegawai.
Susunan Kepegawaian dan operassional
<< Di sinilah Anda akan menguraikan struktur perusahaan yang dimaksud dalam hal manajemen, jumlah karyawan, dan persyaratan operasional fisik untuk menghasilkan atau memasok produk atau layanan. >>
Bagan Organisasi Manajemen (termasuk CEO)
<< Sertakan diagram cara di mana manajemen usaha baru yang akan diselenggarakan. Ini harus menunjukkan bidang tanggung jawab masing-masing manajer dan karyawan yang akan diambil selama tiga tahun ke depan. >>
Bagan Organisasi Fungsional
Siapa yang akan bertanggung jawab kepada siapa? Contohnya: Manager restaurant akan bertanggung jawab kepada CEO dan laporan harian akan diberikan kepada CEO, dll.
Kepegawaian
<< Nyatakan apa yang akan diambil karyawan selama tiga tahun ke depan, dengan keterampilan apa, di bidang bisnis apa. >>
Asisten / Petugas Kantor
Untuk melakukan operasi yang lancar, masing-masing Direktur akan memiliki Asisten / Kantor Clerck.
Pengemudi dan Pengantar Barang (Delivery)
Tugas utama pengirim akan mencakup pengiriman perencanaan (waktu yang tepat, hari yang tepat); memuat dan menurunkan produk dengan hati-hati, mengamankan tanaman dan bunga selama transportasi; memperbaiki, mengembalikan, dan mengganti produk yang rusak karena transit; melacak pengiriman; dan melakukan transaksi kartu kredit di tempat.
Posisi ini akan diamankan melalui agen tenaga kerja lokal, dan akan bekerja paruh waktu. Berdasarkan proyeksi penjualan untuk tahun pertama, seorang pengirim akan diminta sekitar dua jam per hari, empat hari per minggu pada tahun pertama; jam yang dibutuhkan akan meningkat secara proporsional dengan penjualan di tahun dua dan tiga.
Karakteristik: sopan, berpengetahuan luas, rapi dan bersih. Orang tersebut harus mengetahui wilayah tersebut.
Bantuan Sementara
BUKA CAFÉ OFFICE akan mempekerjakan karyawan sementara melalui agen kepegawaian lokal untuk membantu penjualan dan layanan pelanggan sebelum Hari Valentine, Hari Ibu, Paskah / Paskah, Ramadhan / Idul Fitri dan Natal.
Rencana Pelatihan (Training)
<< Menjabarkan rencana pengembangan karyawan dan manajemen yang akan dilakukan untuk mempertahankan tenaga kerja yang terampil. Ini juga harus dikaitkan dengan perkembangan pasar di masa depan dan setiap pengembangan produk atau layanan baru. >>
Dengan menghargai karyawan di setiap tahap dalam karier mereka, kami menginspirasi kesetiaan dan memberikan titik sentuh penting bagi para manajer.
Karyawan senior kami akan mengikuti pelatihan selama setidaknya 2 tahun sekali, untuk memastikan bahwa keterampilan mereka masih mutakhir dengan lingkungan bisnis yang sebenarnya.
Perusahaan juga menawarkan manajemen karir pribadi yang menarik, sebagai janji untuk menumbuhkan komitmen staf terhadap tujuan strategis Perusahaan, serta untuk mempromosikan budaya perusahaan Perusahaan. Selain itu, Perusahaan juga menyediakan program bantuan pendidikan, yang diberikan kepada
staf terpilih yang mengikuti pendidikan formal di sekolah / universitas mana saja di Indonesia. Di bawah program ini, Perusahaan mengganti biaya staf yang memenuhi syarat untuk bagian yang disepakati dari biaya yang terkait dengan kegiatan pendidikannya.
6.4 Operasi
<< Nyatakan persyaratan fisik bisnis:
• Tempat
• Peralatan
• Fasilitas produksi
• Infrastruktur
• Fasilitas komunikasi
• Biaya yang terlibat
• Pemasok >>
Hukum Sumber Daya Manusia dan Ketenagakerjaan Indonesia
Undang-Undang Ketenagakerjaan Indonesia, yang dikeluarkan pada tahun 2003, mendorong perlindungan pekerja dengan menerapkan langkah-langkah yang dirancang untuk meresmikan hubungan antara pengusaha dan karyawan. Mencakup kesejahteraan pekerja adalah semangat utama UU Ketenagakerjaan.
Berikut ini adalah poin-poin penting yang perlu diperhatikan sehubungan dengan pekerjaan di Indonesia:
Kontrak kerja
Undang-undang Ketenagakerjaan Indonesia menyatakan bahwa pekerjaan dapat dibuat secara lisan dan tertulis. Untuk menghindari perselisihan hukum, yang terbaik adalah memiliki kontrak kerja secara tertulis.
Ada dua jenis kontrak kerja:
a. Kontrak jangka tetap.
b. Kontrak kerja permanen.
Kontrak dengan jangka waktu tertentu hanya dapat digunakan untuk jenis pekerjaan tertentu, yaitu pekerjaan musiman atau pekerjaan yang akan diselesaikan dalam periode waktu tertentu.
Kontrak dwibahasa diizinkan. Namun, jika dalam sengketa dan interpretasi antara kedua bahasa berbeda, versi bahasa Indonesia akan menang.
Perekrutan staf
Perekrutan staf dapat dilakukan dengan perekrutan langsung atau outsourcing. Rekrutmen langsung sangat umum di mana hubungan kerja antara majikan dan karyawan.
Rekrutmen outsourcing adalah ketika perusahaan outsourcing pihak ketiga menyediakan karyawannya kepada majikan, dan hanya diperbolehkan bagi pekerja yang terlibat dalam kegiatan non-inti seperti petugas kebersihan, keamanan, dll.
Hak karyawan
Sebuah. Jam kerja
Jam kerja normal adalah 7 jam per hari atau 40 jam per minggu selama 6 hari kerja dalam seminggu atau 8 jam per hari dan 40 jam per minggu selama 5 hari kerja dalam seminggu.
Bekerja melebihi jam kerja normal biasanya dianggap sebagai lembur. (waktu dapat berubah-ubah tergantung UU terbaru).
dan pekerja berhak atas kompensasi untuk itu, kecuali untuk pekerja dalam peran manajemen. Waktu istirahat normal akan menjadi minimal.
13. Rencana keuangan
Financial plan atau rencana keuangan adalah evaluasi komprehensif dari gaji individu saat ini dan keadaan keuangan masa depan dengan menggunakan variabel yang diketahui saat ini untuk memprediksi pendapatan masa depan, nilai aset, dan rencana pendapatan.
Ini sering termasuk anggaran yang mengatur keuangan individu dan kadang-kadang mencakup serangkaian langkah atau tujuan khusus untuk pengeluaran dan tabungan di masa depan. Rencana ini mengalokasikan pendapatan masa depan untuk berbagai jenis pengeluaran, seperti sewa atau utilitas, dan juga mencadangkan sebagian pendapatan untuk tabungan jangka pendek dan jangka panjang. Suatu rencana keuangan kadang-kadang disebut sebagai rencana investasi, tetapi dalam keuangan pribadi suatu rencana keuangan dapat fokus pada bidang-bidang spesifik lainnya seperti manajemen risiko, perkebunan, perguruan tinggi, atau pensiun.
Pastikan Anda mengetahui hal-hal dibawah ini tentang keuangan:
- Laporan Keuangan Konsolidasi – Pengertian dan Contoh Soal Dalam Akuntansi
- Nilai Masa Uang – Time Value of Money (TVM) – Soal dan Jawaban
- Rumus Modal, Laba Rugi, Neraca (Financial statement) dalam Akuntansi – Laporan Keuangan
- Rumus Matematika Keuangan & Contoh Soal dan Jawaban
- Akuntansi – Definisi, Pengertian, Siklus Akuntansi Laporan Keuangan Perusahaan Jasa dan Dagang
- Penggolongan Akun dalam Akuntansi
- Akuntansi FIFO dan LIFO – Beserta Contoh Soal dan Jawaban
- Istilah Akuntansi Inggris-Indonesia
- Rumus Akuntansi & Rumus Dasar, Metode, Penyusutan, HPP, Perusahaan Dagang / Jasa
- Jenis Pajak-Pajak, Tarif, Manfaat Pajak di Indonesia
Persyaratan Pendanaan
<< Nyatakan di sini total kebutuhan pendanaan bisnis, dan bagaimana hal itu dimaksudkan untuk disediakan. Anda juga perlu menyebutkan perkiraan bagaimana dana ini digunakan.
Sumber:
• Dana promotor
• Pinjaman bank
• Hibah atau pinjaman dari lembaga
• Investasi sudah diterima
• Investasi dicari
Dibutuhkan untuk:
• Peralatan
• R&D
• Pemasaran
• Pegawai dan staf >>
Kebijakan Akuntansi
Kebijakan Kredit dan Penagihan
Buku manual dirancang untuk memberikan pedoman dasar dan informasi di bidang kredit & pengumpulan melalui setiap situasi yang melibatkan kredit yang mungkin ditemui seseorang mungkin berbeda.
Pencegahan masalah tidak membayar:
- Periksa pesanan dengan benar.
- Pemeriksaan cash dengan seksama.
- Kartu kredit yang diterima: Visa, masterCard dan American Express.
- Menaruh di bank setiap harinya untuk cash pembayaran dari klien.
- Check tidak dapat diterima di BUKA CAFE.
- Setiap pemesanan harus langsung dibayar oleh klien.
- Pembayaran pajak sebelum jatuh tempo, agar tidak membayar denda.
Baca juga ? Rumus Modal, Laba Rugi, Neraca (Financial statement) dalam Akuntansi – Laporan Keuangan
Contoh rencana keuangan:
| REVENUE | BUDGET Jan | BUDGET Feb | BUDGET Mar | BUDGET Apr | BUDGET May | BUDGET June | BUDGET July | BUDGET Aug | BUDGET Sept | BUDGET Oct | BUDGET Nov | BUDGET Dec | BUDGETTotal in Rp | BUDGET % |
| OUTLET ABC MALL | ||||||||||||||
| Fried Potaes | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 141 750 000 | 7,51% |
| Sate / skewer Chicken | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 22 500 000 | 285 000 000 | 15,11% |
| Sate / skewer Beef | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 342 000 000 | 18,13% |
| Nasi | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 57 000 000 | 3,02% |
| Sausage: Chicken | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 12 750 000 | 155 250 000 | 8,23% |
| Stick Fried Chicken | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 18 000 000 | 228 000 000 | 12,09% |
| Stick Fried Beef | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 27 000 000 | 334 500 000 | 17,73% |
| Dessert crêpes | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 11 250 000 | 138 750 000 | 7,36% |
| Drinks: soda | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 9 000 000 | 111 000 000 | 5,88% |
| Drinks: tea, coffee | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 7 500 000 | 93 000 000 | 4,93% |
| Outlets Revenue | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 150 750 000 | 1 886 250 000 | 100,00% |
| COST OF SALES & DEPARTMENTAL EXPENSES | BUDGET Feb | BUDGET Mar | BUDGET Apr | BUDGET May | BUDGET June | BUDGET July | BUDGET Aug | BUDGET Sept | BUDGET Oct | BUDGET Nov | BUDGET Dec | BUDGETTotal in Rp | BUDGET % | |
| OUTLET ABC MALL | ||||||||||||||
| Fried Potaes | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 42 525 000 | 7,51% |
| Sate / skewer Ayam | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 6 750 000 | 85 500 000 | 15,11% |
| Sate / skewer Daging | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 102 600 000 | 18,13% |
| Nasi | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 1 350 000 | 17 100 000 | 3,02% |
| Sosis | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 3 825 000 | 46 575 000 | 8,23% |
| Stick Fried Chicken | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 5 400 000 | 68 400 000 | 12,09% |
| Stick Fried Beef | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 8 100 000 | 100 350 000 | 17,73% |
| Dessert crêpes | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 3 375 000 | 41 625 000 | 7,36% |
| Drinks: soda | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 2 700 000 | 33 300 000 | 5,88% |
| Drinks: tea, coffee | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 2 250 000 | 27 900 000 | 4,93% |
| Outlets C.O.S. | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 45 225 000 | 565 875 000 | 100,00% |
| GENERAL & OVERHEADS | BUDGET Feb | BUDGET Mar | BUDGET Apr | BUDGET May | BUDGET June | BUDGET July | BUDGET Aug | BUDGET Sept | BUDGET Oct | BUDGET Nov | BUDGET Dec | BUDGETTotal in Rp | BUDGET % | |
| OUTLETS ABC MALL | ||||||||||||||
| Administrative & General | 1 000 000 | 1 632 176 | 1 632 176 | 1 632 176 | 1 632 176 | 1 632 176 | 1 632 176 | 1 632 176 | 1 632 176 | 1 632 176 | 1 632 176 | 1 632 176 | 18 953 935 | 4,52% |
| Marketing | 1 000 000 | 2 845 455 | 2 845 455 | 2 845 455 | 2 845 455 | 2 845 455 | 2 845 455 | 2 845 455 | 2 845 455 | 2 845 455 | 2 845 455 | 2 845 455 | 32 300 000 | 7,70% |
| Salaries | 11 750 000 | 10 750 000 | 20 550 000 | 20 550 000 | 20 550 000 | 20 550 000 | 20 550 000 | 20 550 000 | 20 550 000 | 20 550 000 | 20 550 000 | 20 550 000 | 228 000 000 | 54,32% |
| Telephone / mobile | 200 000 | 1 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 21 200 000 | 5,05% |
| Water | 350 000 | 350 000 | 350 000 | 350 000 | 350 000 | 350 000 | 350 000 | 350 000 | 350 000 | 350 000 | 350 000 | 350 000 | 4 200 000 | 1,00% |
| Energy Costs | 500 000 | 1 000 000 | 2 000 000 | 2 000 000 | 2 000 000 | 4 000 000 | 4 000 000 | 4 000 000 | 4 000 000 | 4 000 000 | 4 000 000 | 4 000 000 | 35 500 000 | 8,46% |
| Property Op. & Maintenance | 1 000 000 | 0 | 200 000 | 200 000 | 200 000 | 200 000 | 200 000 | 200 000 | 200 000 | 200 000 | 200 000 | 200 000 | 3 000 000 | 0,71% |
| Management Fees | 0 | 0 | 1 507 500 | 1 507 500 | 1 507 500 | 1 507 500 | 1 507 500 | 1 507 500 | 1 507 500 | 1 507 500 | 1 507 500 | 1 507 500 | 15 075 000 | 3,59% |
| Transport / bensin / parkir | 1 000 000 | 5 500 000 | 5 500 000 | 5 500 000 | 5 500 000 | 5 500 000 | 5 500 000 | 5 500 000 | 5 500 000 | 5 500 000 | 5 500 000 | 5 500 000 | 61 500 000 | 14,65% |
| Total General & Overhead Exps | 16 800 000 | 23 077 630 | 36 585 130 | 36 585 130 | 36 585 130 | 38 585 130 | 38 585 130 | 38 585 130 | 38 585 130 | 38 585 130 | 38 585 130 | 38 585 130 | 419 728 935 | 100,00% |
| GROSS OPERATING PROFIT | 88 725 000 | 82 447 370 | 68 939 870 | 68 939 870 | 68 939 870 | 66 939 870 | 66 939 870 | 66 939 870 | 66 939 870 | 66 939 870 | 66 939 870 | 66 939 870 | 900 646 065 | 47,75% |
| FIXED EXPENSES | BUDGET Feb | BUDGET Mar | BUDGET Apr | BUDGET May | BUDGET June | BUDGET July | BUDGET Aug | BUDGET Sept | BUDGET Oct | BUDGET Nov | BUDGET Dec | BUDGETTotal in Rp | BUDGET % | |
| Financial Charges Bank Interest | 250 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 4 500 000 | 45 250 000 | 4,91% | |
| Financial Charges Bank Loan | 0 | 0,00% | ||||||||||||
| Insurance | 4 000 000 | 4 000 000 | 0,00% | |||||||||||
| Depreciation | 3 813 889 | 3 813 889 | 3 813 889 | 3 813 889 | 5 480 556 | 5 702 778 | 6 036 111 | 6 036 111 | 6 036 111 | 6 036 111 | 6 036 111 | 56 619 444 | 6,58% | |
| Lease Rental | 35 000 000 | 800 000 | 14 385 000 | 14 385 000 | 14 385 000 | 18 551 667 | 17 751 667 | 17 751 667 | 17 751 667 | 17 751 667 | 17 751 667 | 17 751 667 | 204 016 669 | 19,35% |
| Barter Costs | 61 775 000 | 61 775 000 | 61 775 000 | 185 325 000 | 67,34% | |||||||||
| Incentive Fees | 2 218 125 | 1 723 497 | 1 723 497 | 1 723 497 | 1 673 497 | 1 673 497 | 1 673 497 | 1 673 497 | 1 673 497 | 1 673 497 | 1 673 497 | 20 454 967 | 1,82% | |
| Other Exps Incl. F.F.& E. | 0 | 0,00% | ||||||||||||
| Total Fixed Expenses | 37 218 125 | 66 638 889 | 28 422 386 | 24 422 386 | 24 422 386 | 30 205 720 | 91 402 942 | 29 961 275 | 29 961 275 | 29 961 275 | 29 961 275 | 91 736 275 | 515 666 080 | 100,00% |
| Net Profit Before Tax | 51 506 875 | 15 808 481 | 40 517 484 | 44 517 484 | 44 517 484 | 36 734 150 | -24 463 072 | 36 978 595 | 36 978 595 | 36 978 595 | 36 978 595 | -24 796 405 | 384 979 985 | 20,41% |
14. Lampiran dan tonggak sejarah (milestone)
Setiap tonggak bisnis harus mencakup:
- Deskripsi tugas.
- Tanggal jatuh tempo.
- Anggaran.
- Orang yang bertanggung jawab.
Tonggak sejarah adalah kunci manajemen
Anda akan menggunakan tonggak untuk mengelola bisnis Anda dengan lebih baik. Sekali sebulan, ketika Anda bertemu dengan tim Anda untuk meninjau strategi bisnis dan nomor bisnis Anda, Anda akan meninjau tonggak sejarah Anda untuk memastikan rencana Anda berada di jalur yang benar. Jika ada masalah atau perubahan, ini adalah saat Anda dapat melakukan koreksi kursus.
Meninjau tonggak pencapaian Anda setiap bulan memberi Anda lebih banyak peluang untuk menemukan masalah dan mengidentifikasi peluang. Jika Anda hanya memeriksa kemajuan Anda sekali dalam seperempat, atau berpotensi hanya sekali dalam setahun, Anda memiliki lebih sedikit peluang untuk menyesuaikan arah dan mengubah arah. Di hampir setiap bisnis, selalu ada informasi baru untuk meninjau dan mengubah apa yang diinginkan dan dibutuhkan pelanggan Anda. Tinjauan yang sering tentang sasaran Anda memungkinkan Anda untuk gesit dan menyesuaikan diri dengan cepat ketika Anda membutuhkannya. Untuk selengkapnya tentang mengapa Anda harus sering meninjau tonggak dan metrik bisnis lainnya, lihat posting saya tentang topik ini.
3 jenis tonggak sejarah
Saat Anda membangun dan menumbuhkan bisnis, Anda harus menjadwalkan tiga jenis tonggak yang berbeda:
- Review rencana.
- Validasi asumsi.
- Pelaksanaan.
Review rencana
Semua bisnis harus memiliki tonggak “rencana tinjauan”. Ini mungkin tonggak paling penting yang Anda buat.
Tonggak rencana tinjauan menyisihkan waktu untuk meninjau strategi bisnis, taktik, ramalan, dan anggaran Anda. Jika Anda tidak secara teratur memeriksa paket dan melakukan penyesuaian, Anda dapat dengan mudah keluar jalur. Bukan berarti Anda harus mengikuti rencana secara membabi buta, baik. Sebagai gantinya, rapat tinjauan rencana reguler akan memberi Anda kesempatan untuk melihat apa yang berfungsi, apa yang tidak, dan merevisi saat Anda pergi.
Untuk startup tahap awal, mungkin hanya sedikit dari Anda yang berkumpul dan mungkin tidak banyak cara pendapatan atau biaya untuk meninjau. Tidak apa-apa. Sebagai gantinya, rapat bulanan Anda akan fokus pada langkah-langkah selanjutnya yang dapat Anda ambil untuk menjadikan ide bisnis Anda kenyataan, dan kemajuan apa yang telah Anda buat sejauh ini. Anda akan meninjau kemajuan Anda dalam menerapkan strategi dan taktik Anda, seperti mengembangkan kampanye pemasaran baru, meningkatkan jumlah pelanggan yang membuat pesanan kedua sebesar 15%, atau menandatangani sewa di ruang kantor baru.
Tonggak sejarah untuk memvalidasi asumsi Anda
Saat Anda baru memulai bisnis dan mencari tahu jika Anda memiliki strategi yang tepat, Anda akan membuat tonggak untuk membantu Anda memvalidasi asumsi Anda. Tonggak ini akan digunakan untuk mewawancarai pelanggan potensial untuk mencari tahu apakah mereka memiliki masalah yang Anda pikir mereka miliki, dan untuk mengetahui apakah mereka tertarik dengan solusi Anda. Anda juga akan bekerja untuk mencoba dan mencari tahu seperti apa seharusnya harga Anda.
Ingat, di masa-masa awal bisnis Anda, Anda membuat banyak tebakan – asumsi, betul – tentang apa yang dibutuhkan dan diinginkan pelanggan Anda. Strategi awal Anda adalah sekumpulan tebakan tentang masalah yang dimiliki pelanggan potensial Anda, bagaimana mereka ingin masalah mereka diselesaikan, dan apa yang mereka bayarkan untuk solusi Anda. Tonggak pencapaian Anda pada tahap ini harus diarahkan untuk memvalidasi asumsi-asumsi tersebut sehingga Anda dapat membangun bisnis yang sukses.
Beberapa contoh tonggak sejarah
- Wawancarai 20 pelanggan potensial di segmen pasar utama Anda.
- Meneliti harga untuk pesaing Anda.
- Buat brosur sampel untuk bisnis saya dan lihat apa yang dipikirkan calon pelanggan.
- Tonggak yang Anda buat pada tahap ini harus difokuskan pada tujuan menemukan apa yang disebut “produk / pas pasar.” Ini berarti bahwa Anda telah menemukan target pasar yang tertarik untuk membeli produk Anda dan bahwa produk Anda memecahkan masalah nyata untuk pelanggan Anda.
Sangat mungkin Anda mengetahui bahwa Anda tidak memiliki produk / pasar yang baik. Tidak apa-apa. Sangat mudah untuk membuat perubahan pada strategi Anda, menghasilkan asumsi baru, dan kembali dan mengujinya lagi dengan pelanggan potensial Anda. Itulah manfaat memvalidasi asumsi Anda di awal proses startup bisnis – Anda belum berinvestasi terlalu banyak dalam membangun bisnis Anda dan dapat dengan mudah mengubah arah jika perlu.
Menerapkan strategi Anda
Setelah asumsi Anda divalidasi, Anda akan mulai membuat tonggak implementasi. Ini adalah tugas yang akan Anda lakukan untuk benar-benar membangun bisnis Anda. Anda akan melakukan hal-hal seperti membangun produk Anda, mendirikan kantor atau toko Anda, mengembangkan situs web Anda, dan banyak lagi.
Tonggak implementasi biasanya untuk perusahaan yang telah maju dari tahap awal memulai dan memiliki strategi yang terbukti bahwa mereka tahu akan berhasil. Tonggak sejarah ini adalah tentang menyelesaikan sesuatu darimana yang belum ada dan karena kerja keras Anda menjadi ada hasilnya.
Ini berarti bahwa Anda telah menemukan target pasar yang tertarik untuk membeli produk Anda dan bahwa produk Anda memecahkan masalah nyata untuk pelanggan Anda.
Tanya Jawab Seputar Bisnis Plan
Apakah Bisnis Plan?
Bisnis plan adalah dokumen formal sebuah perusahaan yang berisi tujuan bisnis, metode tentang bagaimana tujuan ini dapat dicapai dan kerangka waktu di mana tujuan ini perlu dicapai. Ini juga menggambarkan sifat bisnis, informasi latar belakang organisasi, proyeksi keuangan organisasi, dan strategi yang ingin diterapkan untuk mencapai target yang dinyatakan. Secara keseluruhan, dokumen ini berfungsi sebagai “peta jalan” yang memberikan arahan bagi bisnis.
Mengapa Anda memerlukan bisnis plan atau rencana bisnis?
Rencana bisnis adalah dokumen tertulis yang menggambarkan bisnis Anda. Ini mencakup tujuan, strategi, penjualan, pemasaran dan perkiraan keuangan.
Rencana bisnis membantu Anda untuk:
- Mengklarifikasi ide bisnis Anda.
- Menemukan potensi masalah.
- Mentukan tujuan Anda.
- Mengukur kemajuan Anda.
Tips menulis bisnis plan
- Singkat, pendek dan jelas
Sangatlah penting bagi calon investor untuk memahami apa arti bisnis Anda dari pandangan sekilas pada rencana Anda. Pastikan Anda memasukkan ringkasan bisnis Anda, dan bagaimana hal itu akan menghasilkan uang sejak awal, dan gunakan bahasa sederhana di seluruh.
- Lebih spesifik
Menjadi spesifik sama pentingnya dengan ringkas. Detailnya akan membantu Anda menelusuri bagaimana Anda akan benar-benar menyampaikan rencana Anda.
- Kenali pasar Anda
Sebagian besar mengetahui apakah bisnis Anda akan berhasil adalah memahami audiens Anda. Pastikan rencana Anda jelas tentang target pasar Anda – kepada siapa Anda akan menjual dan berapa banyak perusahaan lain yang sudah menjual produk serupa?
- Ketahui keuangan Anda
Bagian penting lain dari rencana bisnis adalah bagian keuangan. Jika bisnis Anda tidak menghasilkan uang, itu tidak akan berhasil sehingga Anda harus sangat jelas tentang bagaimana Anda akan mendapat untung. Gunakan untuk keuntungan Anda – rencana Anda akan sangat berguna dalam hal mengamankan pinjaman dan investasi, tetapi itu bukan hanya digunakan. Ini juga merupakan alat pribadi untuk membantu Anda memahami tujuan Anda.
Bacaan Lainnya
- Etika Bisnis – Penjelasan dan Contoh (Tata Krama Dalam Berbisnis)
- Analisis Pesaing – Competitor Analysis dalam Bisnis dan Contohnya – Cara Melakukan Analisis Pesaing atau Analisis Kompetitif
- Pengertian, jenis dan contoh dari bentuk badan usaha: PT, CV, FIRMA, UD, BUMN, BUMD, KOPERASI, YAYASAN
- 15 Faktor Kegagalan Dalam Bisnis atau Wirausaha
- 7 Cara Menjadi Pebisnis Muda yang Handal (UKM Usaha Kecil Menengah)
- 10 Cara Menjadi Pengusaha Sukses dan Bisnis Anda Lancar
- Cara Memilih Asuransi Rumah Untuk Pembeli Yang Pintar
- Prinsip Peter – Manajer Tidak Kompeten
- Pengertian Inflasi Contoh, Indikator, Pengelompokan, Cara Mengatasi & Menghitung
- Pengertian Deflasi Contoh, Jenis, Penyebab, Pengaruh, Cara Mengatasi
- Jakarta Ibu Kota Indonesia: Lahir Pada Tanggal 22 Juni 1527
- Daftar Hari Penting Di Indonesia: Hari Libur / Hari Besar / Hari Raya Keagamaan
- Mengapa Suhu Udara Lebih Dingin Saat Ketinggian Tempat Meningkat?
- Kanker Payudara Penularan, Penyebab, Gejala, Perawatan, Pencegahan, Diteksi Dini
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “oooh begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Cambridge, The Balance
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing