Kerucut (rumus geometri)

Dalam geometri, kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk. Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang miring yang disebut selimut kerucut. Temukan dibawah ini rumus kerucut beserta contoh-contoh soal dan jawabannya.

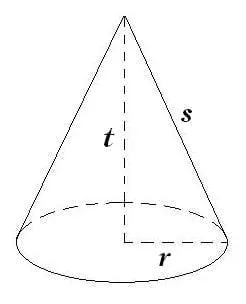
Rumus kerucut

Luas alas

$L=\pi r^{2}$

Luas selimut

$L=\pi rs$

Luas permukaan

$L=\ LuasLingkaran+LuasSelimut$
$=\pi r^{2}+\pi rs$ , atau
$=\pi r\cdot (r+s)$

Volume

$V={\frac {1}{3}}\cdot \pi r^{2}\cdot t$

Soal dan Jawaban Kerucut

1. Sebuah kerucut memiliki diameter 14 cm. Jika tingginya 12 cm, hitunglah volume kerucut tersebut?

Jawaban:
diameter = 14 cm
jari-jari = 1/2 x diameter = 1/2 x 14 = 7 cm

Volume = 1/3 x 22/7 x 7 x 7 x 12 = 616 cm³

2. Tentukan volume kerucut beriku b 18cm 10cm Jwb : V = 1/3 × phi. r2. t

Jawaban:

= 1/3 x 22/7 × 7 × 7 × 24
= 1.232 cm3

3. Diketahui tinggi sebuah kerucut 9 cm. Jika jari-jarinya 14 cm, berapakah volume bangun tersebut?

Petunjuk: gunakan rumus kerucut untuk mencari volume: $V={\frac {1}{3}}\cdot \pi r^{2}\cdot t$

Jawaban:
V = ⅓πr².t
V = 1/3 x 22/7 x 14 x 14 x 9
V = 1.848 cm³

4. Diketahui volume sebuah kerucut adalah 8.316 cm³. Tentukan diameter kerucut tersebut jika tingginya 18 cm! (π = 22/7)

V = 1/3πr².t
8.316 = 1/3 x 22/7 x r² x 18
8.316 = 132/7 x r²
r² = 8.316 x 7/132
r² = 441
r = √441
r = 21 cm

d = 2r
d = 2 x 21
d = 42 cm

5. Sebuah kerucut memiliki tinggi 14 cm. Jika jari-jari kerucut tersebut 8 cm, berapakah volume bangun tersebut? (π = 3,14)

Petunjuk: gunakan rumus kerucut untuk mencari volume: $V={\frac {1}{3}}\cdot \pi r^{2}\cdot t$

Jawaban:
V = 1/3 x 3,14 x 8 x 8 x 14 = 937,81 cm³

6. Sebuah lingkaran memiliki luas 40cm2. Jika lingkaran tersebut dibuat menjadi kerucut dengan tinggi 9 cm, hitung volume kerucut tersebut.

Jawaban:

Diketahui:

t = 9 cm
Luas : L = π x r2 = 40 cm2 .
V = 1/3 x π x r2 x t
= 1/3 x 40 x 9 (ingat : π x r2 = 40 cm2)
= 120 cm3.

Jadi Volume kerucut adalah 120 cm3.

7. Diketahui sebuah kerucut memiliki jari-jari sebesar 3 cm dan panjang garis pelukisnya adalah 5 cm. Maka tentukanlah:

A. tingi kerucut.
B. volume kerucut
C. luas selimut kerucut
D. luas permukaan kerucut

Jawaban:

A. Tinggi kerucut

Untuk mengetahui tinggi kerucut, kita bisa gunakan rumus phytagoras seperti ini:

t2 = s² – r²t2 = 5² – 3²t2 = 25 – 9
t2 = 16
t = √16 = 4cm

B. Volume kerucut

V = 1/3 π r² t
V = 1/3 x 3,14 x 3 x 3 x 4
V = 3.768 cm³

C. Luas selimut kerucut

L = π r s
L = 3,14 x 3 x 5
L = 471 cm²

D. Luas permukaan kerucut

L = π r (s + r)
L = 3,14 x 3 (5 + 3)
L = 3,14 x 3 x 8 = 75,36 cm²

8. Sebuah nasi tumpeng dengan bentuk kerucut sempurna memiliki tinggi 30 cm. Jika panjang jari-jari kerucut adalah 10 cm, berapakah volume nasi tumpeng tersebut?

Jawab :

Diketahui :

t = 30 cm
r = 10 cm
V = 1/3 x π x r2 x t
= 1/3 x 3,14 x 102 x 30
= 1/3 x 3,14 x 100 x 30
= 3140 cm3

Jadi Volume nasi tumpeng berbentuk kerucut tersebut adalah 3140 cm3.

9. Tentukan volume kerucut terpancung jika diameter alasnya 10 dm, diameter sisi atas 4 dm, dan tinggi 4 dm! Jari-jari alas = 5dm , Jari-jari atas = 2dm Jwb : V = phi×t (R.alas2 + R.alas × R.atas + R.atas2 )

Jawaban:

= 3,14×4dm (5dm×5dm + 5dm×2dm + 2dm×2dm)
= 12,56dm (25dm2 + 10dm2 + 4dm2)
= 12,56dm (39dm2)
= 12,56dm × 39dm2
= 489,84dm3

10. Sebuah kerucut memiliki volume 2.009,6 cm³ dan jari-jari 8 cm. Hitunglah tinggi kerucut tersebut! (π = 3,14)

V = 1/3πr².t
2.009,6 = 1/3 x 3,14 x 8 x 8 x t
2.009,6 = t/3 x 200,96

2.009,6/200,96 = t/3
10 = t/3
t = 10 x 3
t = 30 cm

11. Sebuah kerucut mempunyai volume 27 $cm^{3}$ . Jika diameter kerucut diperbesar 3 kali dan tingginya diperbesar 2 kali, maka volume kerucut tersebut adalah…

Pembahasan:
Misalkan jari-jari kerucut pertama adalah $r_{1}$ maka,

$V_{kerucut} = 27$

$\frac{1}{3} \pi r_1^2t_{1} = 27$

Berdasarkan keterangan pada soal: diameter kerucut diperbesar 3 kali.

$d_{2} = 3 \times d_{1}$

$\frac{1}{2}r_{2} = 3 \times \frac{1}{2} r_{1}$

$r_{2} = 3 \times r_{1}$

Berdasarkan pada soal: tingginya diperbesar 2 kali.

$t_{2} = 2t_{1}$

Sehingga,

$V_{2} = \frac{1}{3} \pi r_2^2 t_{2}$

$V_{2} = \frac{1}{3} \pi \times (3r_{1})^2 \times 2t_{1}$

$V_{2} = \frac{1}{3} \pi \times 9r_1^2 \times 2t_{1}$

$V_{2} = 18 \times \frac{1}{3} \pi r_1^2 t_{1}$

$V_{2} = 18 \times 27 = 486 \; cm^{3}$

Jawaban: 486 cm³

12. Ada sebuah kerucut yang memiliki jari – jari 33 cm. cari dan hitunglah keliling alas kerucut tersebut!

Penyelesaian:

Diketahui: r = 33 cm

ditany: K = …?

Jawaban:

K = 2 πr
K = 2 x 3,14 x 33 cm
K = 207,24 cm

Jadi, keliling alas kerucut tersebut adalah = 207,24 cm

13. Saya memiliki kerucut yang terbuat dari kertas. Jika diameter alas kerucut 10 cm dan tinggi kerucut 15 cm, hitung berapa volume kerucut tersebut?

.Jawaban:

Diketahui:

t = 15 cm
d = 10 cm
r = 1 /2 x d = 1 /2 x 10 = 5 cm
V = 1/3 x π x r2 x t
= 1/3 x 3,14 x 52 x 15
= 1/3 x 3,14 x 25 x 15
= 392,5 cm3.

Jadi Volume kerucut kertas Andi tersebut adalah 392,5 cm3.

14. Doni ingin membuat desain cone untuk es krim dengan volume terisi setidaknya 10 cm3. Bila tinggi cone harus tepat 6 cm, hitung berapa diameter lingkaran minimal.

Jawaban:

Diketahui:

t = 6 cm
V = 10 cm3
V = 1/3 x π x r2 x t
10 = 1/3 x 3,14 x r2 x 6
10 = 6,28 x r2
r2 = 10 /6,28 = 1,59
r = √1,59 = 1,26 cm
d = 2 x r = 2 x 1,26 = 2,52 cm.

Jadi diameter alas kerucut adalah 2,52 cm.

15. Contoh Soal Luas Permukaan Kerucut : Jika diameter sebuah kerucut adalah 10 cm dan tingginya 12 cm, tentukanlah:

Panjang garis pelukis (s).
Luas selimut kerucut.
Luas permukaan kerucut.

Jawaban:

Diketahui: d = 10 maka r = 10/2 = 5 cm
t = 12 cm

Ditanyakan :

Panjang garis pelukis (s)
Luas selimut kerucut
Luas permukaan kerucut.

Penyelesaian:

1.) Panjang garis pelukis (s2) = r2 + t2
= 52 + 122
= 25 + 144
s2 = 169 cm
Jadi, panjang garis pelukis kerucut tersebut adalah 13 cm.

2.) Luas selimut kerucut = πrs
= 3,14 · 5 · 13
= 204,1
Jadi, luas selimut kerucut tersebut adalah 204,1 cm2.

3.) Luas permukaan kerucut = πr (s + r)
= 3,14 · 5 · (13 + 5)
= 282,6
Jadi, luas permukaan kerucut tersebut adalah 282,6 cm2.

Rumus Tetrahedron Geometri 3 Dimensi Beserta Contoh Soal dan Jawaban

Tetrahedron geometri adalah bentuk geometrik 3 dimensi. Ini adalah polihedron terkecil. Hal ini terdiri 4 wajah segitiga, 3 dari yang bergabung di setiap sudut. Angka ini digunakan secara luas dalam arsitektur dan seni modern. Tetrahedron juga digunakan untuk memecahkan masalah geometris yang rumit. Klik disini untuk mengetahui lebih lanjut (akan membuka layar baru).

Bacaan Lainnya

Sumber bacaan: Math Warehouse, Varsity Tutors

Rumus Kerucut Berserta Contoh Soal dan Jawaban

Kerucut (rumus geometri)

Rumus kerucut

Luas alas

Luas selimut

Luas permukaan

Volume

Soal dan Jawaban Kerucut

1. Sebuah kerucut memiliki diameter 14 cm. Jika tingginya 12 cm, hitunglah volume kerucut tersebut?

2. Tentukan volume kerucut beriku b 18cm 10cm Jwb : V = 1/3 × phi. r2. t

3. Diketahui tinggi sebuah kerucut 9 cm. Jika jari-jarinya 14 cm, berapakah volume bangun tersebut?

4. Diketahui volume sebuah kerucut adalah 8.316 cm³. Tentukan diameter kerucut tersebut jika tingginya 18 cm! (π = 22/7)

5. Sebuah kerucut memiliki tinggi 14 cm. Jika jari-jari kerucut tersebut 8 cm, berapakah volume bangun tersebut? (π = 3,14)

6. Sebuah lingkaran memiliki luas 40cm2. Jika lingkaran tersebut dibuat menjadi kerucut dengan tinggi 9 cm, hitung volume kerucut tersebut.

A. tingi kerucut.
B. volume kerucut
C. luas selimut kerucut
D. luas permukaan kerucut

8. Sebuah nasi tumpeng dengan bentuk kerucut sempurna memiliki tinggi 30 cm. Jika panjang jari-jari kerucut adalah 10 cm, berapakah volume nasi tumpeng tersebut?

9. Tentukan volume kerucut terpancung jika diameter alasnya 10 dm, diameter sisi atas 4 dm, dan tinggi 4 dm! Jari-jari alas = 5dm , Jari-jari atas = 2dm Jwb : V = phi×t (R.alas2 + R.alas × R.atas + R.atas2 )

10. Sebuah kerucut memiliki volume 2.009,6 cm³ dan jari-jari 8 cm. Hitunglah tinggi kerucut tersebut! (π = 3,14)

11. Sebuah kerucut mempunyai volume 27 $cm^{3}$ . Jika diameter kerucut diperbesar 3 kali dan tingginya diperbesar 2 kali, maka volume kerucut tersebut adalah…

12. Ada sebuah kerucut yang memiliki jari – jari 33 cm. cari dan hitunglah keliling alas kerucut tersebut!

13. Saya memiliki kerucut yang terbuat dari kertas. Jika diameter alas kerucut 10 cm dan tinggi kerucut 15 cm, hitung berapa volume kerucut tersebut?

14. Doni ingin membuat desain cone untuk es krim dengan volume terisi setidaknya 10 cm3. Bila tinggi cone harus tepat 6 cm, hitung berapa diameter lingkaran minimal.

15. Contoh Soal Luas Permukaan Kerucut : Jika diameter sebuah kerucut adalah 10 cm dan tingginya 12 cm, tentukanlah:

Panjang garis pelukis (s).

Luas selimut kerucut.

Luas permukaan kerucut.

Rumus Tetrahedron Geometri 3 Dimensi Beserta Contoh Soal dan Jawaban

Bacaan Lainnya

Pajak Perusahaan Indonesia | Memahami Pajak Badan di Indonesia

Apakah Anda Perlu Menerbitkan Faktur Pajak?

Pajak Tahunan Perusahaan | Pengurangan Tarif, Penghitungan, Penghasilan Kena…

Tinggalkan Balasan Batalkan balasan

Rumus Kerucut Berserta Contoh Soal dan Jawaban

Kerucut (rumus geometri)

Rumus kerucut

Luas alas

Luas selimut

Luas permukaan

Volume

Soal dan Jawaban Kerucut

1. Sebuah kerucut memiliki diameter 14 cm. Jika tingginya 12 cm, hitunglah volume kerucut tersebut?

2. Tentukan volume kerucut beriku b 18cm 10cm Jwb : V = 1/3 × phi. r2. t

3. Diketahui tinggi sebuah kerucut 9 cm. Jika jari-jarinya 14 cm, berapakah volume bangun tersebut?

4. Diketahui volume sebuah kerucut adalah 8.316 cm³. Tentukan diameter kerucut tersebut jika tingginya 18 cm! (π = 22/7)

5. Sebuah kerucut memiliki tinggi 14 cm. Jika jari-jari kerucut tersebut 8 cm, berapakah volume bangun tersebut? (π = 3,14)

6. Sebuah lingkaran memiliki luas 40cm2. Jika lingkaran tersebut dibuat menjadi kerucut dengan tinggi 9 cm, hitung volume kerucut tersebut.

A. tingi kerucut. B. volume kerucut C. luas selimut kerucut D. luas permukaan kerucut

8. Sebuah nasi tumpeng dengan bentuk kerucut sempurna memiliki tinggi 30 cm. Jika panjang jari-jari kerucut adalah 10 cm, berapakah volume nasi tumpeng tersebut?

9. Tentukan volume kerucut terpancung jika diameter alasnya 10 dm, diameter sisi atas 4 dm, dan tinggi 4 dm! Jari-jari alas = 5dm , Jari-jari atas = 2dm Jwb : V = phi×t (R.alas2 + R.alas × R.atas + R.atas2 )

10. Sebuah kerucut memiliki volume 2.009,6 cm³ dan jari-jari 8 cm. Hitunglah tinggi kerucut tersebut! (π = 3,14)

12. Ada sebuah kerucut yang memiliki jari – jari 33 cm. cari dan hitunglah keliling alas kerucut tersebut!

13. Saya memiliki kerucut yang terbuat dari kertas. Jika diameter alas kerucut 10 cm dan tinggi kerucut 15 cm, hitung berapa volume kerucut tersebut?

14. Doni ingin membuat desain cone untuk es krim dengan volume terisi setidaknya 10 cm3. Bila tinggi cone harus tepat 6 cm, hitung berapa diameter lingkaran minimal.

15. Contoh Soal Luas Permukaan Kerucut : Jika diameter sebuah kerucut adalah 10 cm dan tingginya 12 cm, tentukanlah:

Panjang garis pelukis (s).

Luas selimut kerucut.

Luas permukaan kerucut.

Rumus Tetrahedron Geometri 3 Dimensi Beserta Contoh Soal dan Jawaban

Bacaan Lainnya

Pajak Perusahaan Indonesia | Memahami Pajak Badan di Indonesia

Apakah Anda Perlu Menerbitkan Faktur Pajak?

Pajak Tahunan Perusahaan | Pengurangan Tarif, Penghitungan, Penghasilan Kena…

Tinggalkan Balasan Batalkan balasan

A. tingi kerucut.
B. volume kerucut
C. luas selimut kerucut
D. luas permukaan kerucut