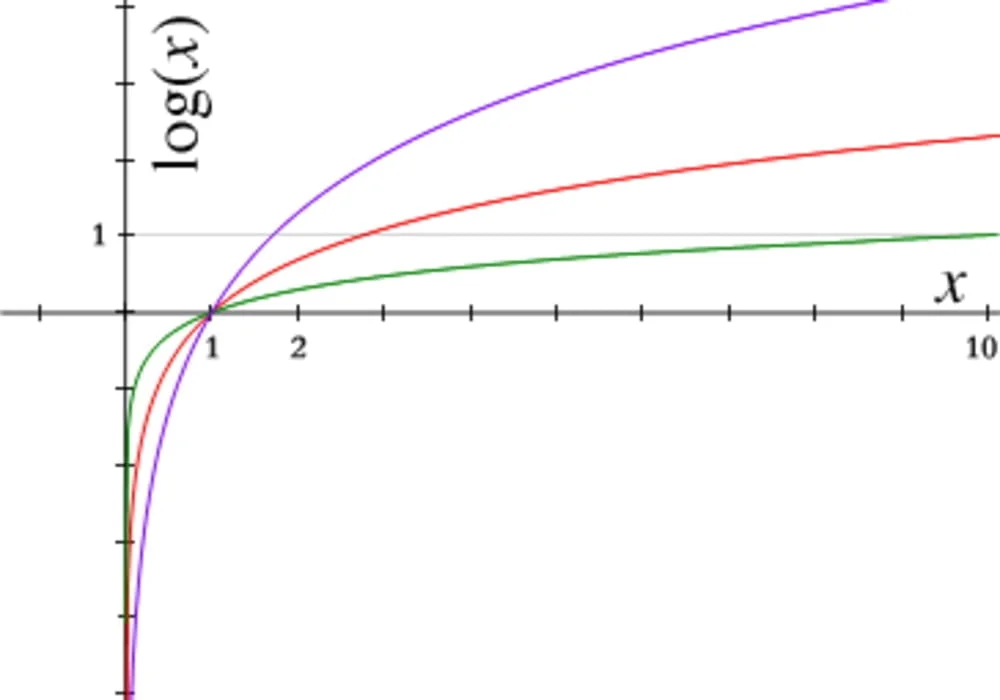
Kegunaan logaritma

Logaritma sering digunakan untuk memecahkan persamaan yang pangkatnya tidak diketahui. Turunannya mudah dicari dan karena itu logaritma sering digunakan sebagai solusi dari integral. Dalam persamaan bn = x, b dapat dicari dengan pengakaran, n dengan logaritma, dan x dengan fungsi eksponensial.

Rumus Logaritma

ac = b → ª log b = c

a = basis
b = bilangan yang dilogaritma
c = hasil logaritma

Sifat Logaritma

ª log a = 1
ª log 1 = 0
ª log aⁿ = n
ª log bⁿ = n • ª log b
ª log b • c = ª log b + ª log c
ª log b/c = ª log b – ª log c
ªˆⁿ log b m = m/n • ª log b
ª log b = 1 ÷ b log a
ª log b • b log c • c log d = ª log d
ª log b = c log b ÷ c log a

Penghitungan nilai logaritma

Nilai logaritma dengan basis b dapat dihitung dengan rumus dibawah ini.

\log _{b}(x)={\frac {\log _{e}(x)}{\log _{e}(b)}}\qquad {\mbox{ atau }}\qquad \log _{b}(x)={\frac {\log _{2}(x)}{\log _{2}(b)}}

Sedangkan untuk logaritma berbasis e dan berbasis 2, terdapat prosedur-prosedur yang umum, yang hanya menggunakan penjumlahan, pengurangan, pengkalian, dan pembagian.

Logaritma memindahkan fokus penghitungan dari bilangan normal ke pangkat-pangkat (eksponen). Bila basis logaritmanya sama, maka beberapa jenis penghitungan menjadi lebih mudah menggunakan logaritma:

Penghitungan dengan angka	Penghitungan dengan eksponen	Identitas Logaritma
$\!\,ab$	$\!\,A+B$	$\!\,\log(ab)=\log(a)+\log(b)$
$\!{\frac {a}{b}}$	$\!\,A-B$	$\!\,\log({\frac {a}{b}})=\log(a)-\log(b)$
$\!\,a^{b}$	$\!\,Ab$	$\!\,\log(a^{b})=b\log(a)$
$\!\,{\sqrt[{b}]{a}}$	$\!\,{\frac {A}{b}}$	$\!\,\log({\sqrt[{b}]{a}})={\frac {\log(a)}{b}}$

Sifat-sifat di atas membuat penghitungan dengan eksponen menjadi lebih mudah, dan penggunaan logaritma sangat penting, terutama sebelum tersedianya kalkulator sebagai hasil perkembangan teknologi modern.

Untuk mengkali dua angka, yang diperlukan adalah melihat logaritma masing-masing angka dalam tabel, menjumlahkannya, dan melihat antilog jumlah tersebut dalam tabel. Untuk mengitung pangkat atau akar dari sebuah bilangan, logaritma bilangan tersebut dapat dilihat di tabel, lalu hanya mengkali atau membagi dengan radix pangkat atau akar tersebut.

Logaritma alami

Adalah logaritma yang berbasis e, di mana e adalah 2,718281828459… (dan seterusnya). Logaritma alami terdefinisikan untuk semua bilangan real positif x dan dapat juga didefinisikan untuk bilangan kompleks yang bukan 0.

Ahli matematika biasanya menggunakan “ln(x)” atau “log(x)” untuk menotasikan log_e(x), atau logaritma alami dari x, dan menggunakan “log₁₀(x)” untuk menotasikan logaritma berbasis 10 dari x.

Insinyur, ahli biologi, dan orang dalam bidang-bidang lain, hanya menggunakan “ln(x)” atau kadang-kadang (untuk supaya lebih jelas) “log_e(x)” untuk menotasikan logaritma natural dari x, dan “log(x)” digunakan untuk logaritma berbasis 10, log₁₀(x) atau, dalam konteks teknik komputer, log₂(x).

Kebanyakan bahasa komputer, termasuk C, C++, Fortran, dan BASIC, “log” atau “LOG” berarti logaritma alami.

Pada kalkulator, tombol ln berarti logaritma alami, sedangkan tombol log adalah untuk logaritma berbasis 10

Secara formal, ln(a) dapat didefinisikan sebagai luas di bawah grafik (integral) dari 1/x dihitung dari 1 ke a, atau,

\ ln(a)=\int _{1}^{a}{\frac {1}{x}}\,dx.

Definisi tersebut mendefinisikan suatu logaritma, karena memenuhi sifat fundamental logaritma, yaitu:

\ ln(ab)=\ln(a)+\ln(b)\,\!

Ini dapat ditunjukkan dengan mendefinisikan $\phi (t)=at$ dan dengan menggunakan rumus substitusi:

\ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt=\ln(a)+\ln(b)

Bilangan e, selanjutnya dapat didefinisikan sebagai bilangan real yang unik a di mana $\ln(a)=1$ .

Ln sebagai invers fungsi eksponensial alami

Fungsi ln adalah invers dari fungsi eksponensial:

\ e^{\ln(x)}=x\,\!

untuk semua x yang positif dan

\ ln(e^{x})=x\,\!

untuk semua x yang real.

Logaritma dapat didefinisikan untuk basis lainnya, asal positif, tidak hanya e, dan biasanya berguna untuk memecahkan persamaan yang variabel tidak diketahuinya merupakan pangkat dari variabel lain.

Logaritma biner

Logaritma biner (bahasa Inggris: binary logarithm) dalam matematika adalah , adalah logaritma dengan basis 2, yang biasanya dilambangkan dengan log₂ n atau ²log n. Merupakan fungsi invers dari fungsi kuadrat atau fungsi pangkat dua. Logaritme biner nadalah kepangkatan bilangan dua untuk mendapatkan nilai n. Jadi:

x=\log _{2}n\quad \Longleftrightarrow \quad 2^{x}=n.

Misalnya:

logaritme biner 1 adalah 0
logaritme biner 2 adalah 1
logaritme biner 4 adalah 2
logaritme biner 8 adalah 3
logaritme biner 16 adalah 4
logaritme biner 32 adalah 5

dan seterusnya

Logaritma biner terkait erat dengan “Sistem bilangan biner”. Dalam sejarahnya, aplikasi pertama logaritme biner adalah dalam teori musik, oleh Leonhard Euler. Bidang lain yang sering menggunakan logaritme biner termasuk teori informasi, combinatorics, computer science, bioinformatika, desain turnamen olahraga, dan fotografi.

Suatu cara mudah untuk menghitung ²log (n) pada kalkulator yang tidak mempunyai fungsi log₂ adalah menggunakan fungsi logaritma natural (ln) atau logaritma umum (log), yang biasanya ada pada kebanyakan scientific calculator. Rumus perubahan basis logaritma adalah:^[15]^[16]

\log _{2}n={\frac {\ln n}{\ln 2}}={\frac {\log _{10}n}{\log _{10}2}},

or approximately

\log _{2}n\approx 1.442695\ln n\approx 3.321928\log _{10}n.

Contoh Soal dan Jawaban Logaritma

1. Jika log 2 = a
maka log 5 adalah…

Jawaban:

log 5 = log (10/2) = log 10 – log 2 = 1 – a (karena log 2 = a)

2. Sederhanakan bentuk berikut: 3 log 5 + log 8 – log 40

Jawaban:

= log 53 + log 8 – log 40
= log 125 + log 8 – log 40
= log
= log 25
= log 52 = 2 log 5

3. Nyatakan bentuk eksponen berikut dalam notasi logaritma 32 = 9

Jawaban:

32 = 9 3log 9 = 2

4. Nilai dari ^√5 log 625 adalah…

Jawaban:

^√⁵ log 625
(√5)^x = 625
(√5)⁸ = 625
X = 8

5. Sederhanakan bentuk berikut: Log 7 + log 2 + log 1/40 + log 1/7

Jawaban:

= log (7 x 2 x 1/10 x 1/7)
= log 1/5
= log 1 – log 5
= log 100 – log 5
= 0 – log 5
= – log 5

6. Nilai dari √15 + √60 – √27 = …

Jawaban:

√15 + √60 – √27
= √15 + √(4×15) – √(9×3)
= √15 + 2√15 – 3√3
= 3√15 – 3√3
= 3(√15 – √3)

7. Log 9 per log 27 =…

Jawaban:

log 9 / log 27
= log 3² / log 3³
= (2. log 3) / (3 . log 3) <– ingat sifat log a^n = n. log a
= 2/3

8. Jika log 2 = 0,3010 dan log 3 = 0,4771, maka log 600 =…

Jawaban:

Diketahui log 2 = 0,3010 dan log 3 = 0,4771
Log 600 = log 2.3.100
= log 2 + log 3 + log 100
= 0,3010 + 0,4771 + 2 = 2,7781

9. Jika ²log 3 = a dan ³log 5 = b, maka ¹⁵log 20 =…

Jawaban:

¹⁵log 20 = ¹⁵log 3 . ³log 20 = ³log 20 / ³log 15,
kita pisah jadi 2 untuk memudahkan mengerjakan
–> ³log 20 = ³log 4 +³log 5 = 2. ³log 2 +³log 5
–> karena ²log 3 = a maka ³log 2 = 1/a
–> 2/a + b = (2+ab)/a ……. (1)–> ³log 15 = ³log 3 + ³log 5 = 1+b ……. (2)jadi hasilnya = (2+ab)/a : (1+b) = 2a+ab/ a (1+b)

10. Jika log 2 = 0,301 dan log 3 = 0,477 maka nilai dari log 225 ?

Pembahasan= 1/3 log 225 = 1/3 log 15² = 2/3 log 15 = 2/3 (log 3 + log 5 )
log 3 sudah diketahui, sekarang bagaimanan dengan log 5 ? .
log 5 bisa didapat dari log 10/2 = log 10 – log 2
= 2/3 (log 3 + log 10 – log 2)
= 2/3 . (0.477 + 1 – 0,301)
= 2/3 . 1,176
= 0,784

11. Persamaan kuadrat 2×²-px+1=0 dengan p>0,mempunyai akar-akar a dan b ,jika x²-5x+q=0 mempunyai akar-akar 1/a² dan 1/b² maka p-q=…

pada persamaan 2×²-px+1=0 –> a = 2 b = -p c = 1
a + b = -b/a = p/2 _…(1)
a.b = c/a = 1/2 _…(2)

pada persamaan
x²-5x+q=0 –> a = 1 b= -5 c = q
1/a² + 1/b² = 5/1 = 5 _…(3)
1/a² . 1/b² = q_…(4)
sekarang kita punya 4 persamaan

1/a² + 1/b² = 5
a² + b² /(ab)² = 5
(a+b)² – 2ab / (ab)² = 5 (kita masukkan persamaan 1 dan 2)
(p/2)² – 2.(1/2) / (1/2)² = 5
(P²/4 – 1) 4 = 5
P² – 4 = 5
p² = 9
p = 3 atau -3

1/a² . 1/b² = q (kita masukkan persamaan 2)
1/(ab)² = q
1/(1/2)² = q
q = 4

Jadi p-q
bisa 3 – 4 = -1
atau
-3 -4 = -7

12. Jika diketahui 2log 3 = x dan 2log 5 = y, maka 2log 45 √15 sama dengan…

Jawaban:

²log 45√(15)= ²log 3².5.(3.5)^1/2= ²log 3².5.3^1/2.5^1/2= ²log 3^5/2 + ²log 5^3/2= (5/2) ²log 3 + (3/2)²log 5
= ½(5x + 3y)

13. Jika ³log 5 = 1,465 dan ³log 7 = 1,771, maka ³log 105 adalah…

Jawaban:

³log5 = 1,465 dan ³log7 = 1,771, maka:
³log105 = ³log3.5.7
=³log3 + ³log5 +³log7
= 1 + 1,465 + 1,771
=4,236

14. Nilai dari √5 -3 per √5 +3 =…

Jawaban:

(√5 – 3)/(√5 + 3)
= (√5 – 3)/(√5 + 3) x (√5 – 3)/(√5 – 3) <– kali akar sekawan
= (√5 – 3)²/(5 – 9)
= -1/4 (5 – 6√5 + 9)
= -1/4 (14 – 6√5)
= -7/2 + 3/2√5
= (3√5 – 7)/2

15. Jika a log 3 = -0,3 tunjukkan bahwa a = 1/81 3√9

Jawaban:

ª log 3 = -0,3
log 3/log a = -0.3
log a = -(10/3)log 3
log a = log [3^(-10/3)] a = 3^(-10/3) = 3^(-4) (3²)^(⅓ )
a= 1/81 3√9

16. Nilai dari ³log 6 + 2. ³log 2 adalah…

Jawaban:

³log 6 + 2. ³log 2
= ³log + 2. ³ log3
= ³log 3 + 2 . 1
= 1 + 2
= 3

17. Log (3a – √2) dengan basis 1/2. Tentukan nilai a!

Jawaban:

[log (3a – √2)]/log(0.5) = -0.5
log (3a – √2) = -0.5 log 0.5 = log (1/√½)
3a – √2 = 1/√½
a = (2/3) √2

18. Jika diketahui log x = a dan log y = b, maka log ….

Jawaban:

log log 10x³ – log y²= log 10 + 3 log x – 2log y
= 1 + 3a – 2b

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Sumber bacaan: Math Insight

Rumus Logaritma Matematika Beserta Contoh Soal dan Jawaban

Kegunaan logaritma

Rumus Logaritma

ac = b → ª log b = c

Sifat Logaritma

Penghitungan nilai logaritma

Logaritma memindahkan fokus penghitungan dari bilangan normal ke pangkat-pangkat (eksponen). Bila basis logaritmanya sama, maka beberapa jenis penghitungan menjadi lebih mudah menggunakan logaritma:

Logaritma alami

Ln sebagai invers fungsi eksponensial alami

Logaritma biner

Contoh Soal dan Jawaban Logaritma

1. Jika log 2 = a
maka log 5 adalah…

2. Sederhanakan bentuk berikut: 3 log 5 + log 8 – log 40

3. Nyatakan bentuk eksponen berikut dalam notasi logaritma 32 = 9

4. Nilai dari ^√5 log 625 adalah…

5. Sederhanakan bentuk berikut: Log 7 + log 2 + log 1/40 + log 1/7

6. Nilai dari √15 + √60 – √27 = …

7. Log 9 per log 27 =…

8. Jika log 2 = 0,3010 dan log 3 = 0,4771, maka log 600 =…

9. Jika ²log 3 = a dan ³log 5 = b, maka ¹⁵log 20 =…

10. Jika log 2 = 0,301 dan log 3 = 0,477 maka nilai dari log 225 ?

11. Persamaan kuadrat 2×²-px+1=0 dengan p>0,mempunyai akar-akar a dan b ,jika x²-5x+q=0 mempunyai akar-akar 1/a² dan 1/b² maka p-q=…

12. Jika diketahui 2log 3 = x dan 2log 5 = y, maka 2log 45 √15 sama dengan…

13. Jika ³log 5 = 1,465 dan ³log 7 = 1,771, maka ³log 105 adalah…

14. Nilai dari √5 -3 per √5 +3 =…

15. Jika a log 3 = -0,3 tunjukkan bahwa a = 1/81 3√9

16. Nilai dari ³log 6 + 2. ³log 2 adalah…

17. Log (3a – √2) dengan basis 1/2. Tentukan nilai a!

18. Jika diketahui log x = a dan log y = b, maka log ….

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

Rumus Logaritma Matematika Beserta Contoh Soal dan Jawaban

Kegunaan logaritma

Rumus Logaritma

ac = b → ª log b = c

Sifat Logaritma

Penghitungan nilai logaritma

Logaritma memindahkan fokus penghitungan dari bilangan normal ke pangkat-pangkat (eksponen). Bila basis logaritmanya sama, maka beberapa jenis penghitungan menjadi lebih mudah menggunakan logaritma:

Logaritma alami

Ln sebagai invers fungsi eksponensial alami

Logaritma biner

Contoh Soal dan Jawaban Logaritma

1. Jika log 2 = a maka log 5 adalah…

2. Sederhanakan bentuk berikut: 3 log 5 + log 8 – log 40

3. Nyatakan bentuk eksponen berikut dalam notasi logaritma 32 = 9

4. Nilai dari √5 log 625 adalah…

5. Sederhanakan bentuk berikut: Log 7 + log 2 + log 1/40 + log 1/7

6. Nilai dari √15 + √60 – √27 = …

7. Log 9 per log 27 =…

8. Jika log 2 = 0,3010 dan log 3 = 0,4771, maka log 600 =…

9. Jika 2log 3 = a dan 3log 5 = b, maka 15log 20 =…

10. Jika log 2 = 0,301 dan log 3 = 0,477 maka nilai dari log 225 ?

11. Persamaan kuadrat 2×2-px+1=0 dengan p>0,mempunyai akar-akar a dan b ,jika x2-5x+q=0 mempunyai akar-akar 1/a2 dan 1/b2 maka p-q=…

12. Jika diketahui 2log 3 = x dan 2log 5 = y, maka 2log 45 √15 sama dengan…

13. Jika 3log 5 = 1,465 dan 3log 7 = 1,771, maka 3log 105 adalah…

14. Nilai dari √5 -3 per √5 +3 =…

15. Jika a log 3 = -0,3 tunjukkan bahwa a = 1/81 3√9

16. Nilai dari 3log 6 + 2. 3log 2 adalah…

17. Log (3a – √2) dengan basis 1/2. Tentukan nilai a!

18. Jika diketahui log x = a dan log y = b, maka log <img decoding="async" class="alignnone size-full wp-image-10995" src="http://banksoal.sridianti.com/wp-content/uploads/2014/08/log1.png" alt="log1" width="55" height="55" /> ….

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

Tinggalkan Balasan Batalkan balasan

1. Jika log 2 = a
maka log 5 adalah…

4. Nilai dari ^√5 log 625 adalah…

9. Jika ²log 3 = a dan ³log 5 = b, maka ¹⁵log 20 =…

11. Persamaan kuadrat 2×²-px+1=0 dengan p>0,mempunyai akar-akar a dan b ,jika x²-5x+q=0 mempunyai akar-akar 1/a² dan 1/b² maka p-q=…

13. Jika ³log 5 = 1,465 dan ³log 7 = 1,771, maka ³log 105 adalah…

16. Nilai dari ³log 6 + 2. ³log 2 adalah…

18. Jika diketahui log x = a dan log y = b, maka log ….