Topologi Matematika

Topologi Matematika merupakan cabang matematika yang bersangkutan dengan tata ruang yang tidak berubah dalam deformasi dwikontinu (yaitu ruang yang dapat ditekuk, dilipat, disusut, direntangkan, dan dipilin, tetapi tidak diperkenankan untuk dipotong, dirobek, ditusuk atau dilekatkan). Karena sifat ini, topologi disebut pula geometri karet.

Ia muncul melalui pengembangan konsep dari geometri dan teori himpunan, seperti ruang, dimensi, bentuk dan transformasi.

Mug and Torus morph — Deformasi terus menerus (sejenis homeomorfisma) dari sebuah cangkir menjadi donat (torus) dan kembali lagi. Sumber foto: LucasVB / Wikimedia Commons

1. Topologi terhadap Himpunan

Istilah topologi matematika juga dipakai untuk sebuah ide matematis yang sangat pokok dalam sebuah cabang matematika yang disebut topologi. Secara sederhana, sebuah topologi memberikan deskripsi bagaimana anggota-anggota dalam sebuah himpunan saling terkait secara spasial (misal kedekatan antara 2 titik).

Himpunan yang sama dapat pula diberikan topologi yang berbeda. Misalkan, garis bilangan real, bidang kompleks, dan himpunan Kantor dapat dianggap sebagai himpunan yang sama tetapi dengan topologi matematika yang berbeda-beda (ketiganya memiliki kardinalitas yang sama).

Secara formal, misalkan X sebuah himpunan dan τ adalah keluarga subhimpunan dari X. Maka τ disebut topologi terhadap X jika:

Himpunan kosong dan X adalah anggota dari τ. $\emptyset ,X\in \tau$
Gabungan anggota-anggota dari τ dengan jumlah sembarang adalah anggota dari τ. ${\bigcup _{i=1}^{n\leq \infty }A_{i}}\in \tau :A_{i}\in \tau$
Irisan anggota-anggota dari τ yang jumlahnya berhingga adalah anggota dari τ. ${\bigcap _{i=1}^{n<\infty }A_{i}}\in \tau :A_{i}\in \tau$

Jika τ adalah topologi terhadap X maka pasangan (X, τ) disebut ruang topologi.

Anggota dari τ disebut himpunan terbuka di dalam X. Sebuah subhimpunan A dari X disebut tertutup jika komplemennya ada di dalam τ (komplemennya terbuka, X ∖ A ϵ τ). Sebuah subhimpunan dari X dapat merupakan himpunan terbuka, tertutup, terbuka dan tertutup, atau tidak kedua-duanya.

Himpunan kosong dan X sendiri masing-masing selalu tertutup dan terbuka. Sebuah subhimpunan N(x) dari X yang merupakan superhimpunan dari sebuah himpunan terbuka U yang memiliki sebagai salah satu anggotanya adalah x disebut tetangga dari x ( $x\in U\subset N(x):U\in \tau$ ).

Definisi melalui hubungan ketetanggaan

Definisi ini dicetuskan oleh Felix Hausdorff. Misalkan X adalah sebuah himpunan, dengan anggota-anggotanya yang sering kali disebut titik-titik, meski sebenarnya bisa obyek matematis apapun. X boleh himpunan kosong. Pilih sebuah fungsi N yang menyematkan kepada setiap titik x sebuah koleksi N(x) keluarga subhimpunan dari X.

Anggota-anggota dari N(x) disebut ketetanggaan dari x terhadap N (atau cukup, ketetanggaan dari x). Fungsi N disebut topologi ketetanggaan jika aksioma-aksioma di bawah terpenuhi; dan pasangan (X, N) adalah sebuah ruang topologi.

Jika N adalah ketetanggaan dari x (N ∈ N(x)), maka x ∈ N. Dalam kata lain, setiap titik merupakan anggota dari ketetanggaannya.
Jika N adalah subhimpunan dari X dan memuat sebuah ketetanggaan dari x, maka N adalah ketetanggaan dari x. Setiap superhimpunan dari ketetanggaan sebuah titik merupakan ketetanggaan titik itu pula.
Irisan dua ketetanggaan dari x adalah sebuah ketetanggaan dari x juga.
Seluruh ketetanggaan N dari x memuat ketetanggaan M dari x sedemikian sehingga N adalah ketetanggaan dari seluruh titik-titik di M.

Tiga aksioma pertama dari hubungan ketetanggaan memiliki maksud yang jelas. Aksioma ke-empat memiliki peran penting dalam menentukan struktur topologi matematika ketetanggaan N, yaitu menentukan hubungan ketetanggaan dari titik-titik yang berbeda.

Contoh umum dari hubungan ketetanggaan adalah sistem ketetanggaan pada garis bilangan riil, dimana N adalah ketetanggaan dari sebuah bilangan riil x jika ia memuat sebuah interval terbuka yang memiliki xsebagai anggotanya.

Dengan struktur demikian, sebuah subhimpunan U dari X disebut subhimpunan terbuka jika U merupakan ketetanggaan bagi seluruh anggotanya.

Definisi melalui himpunan terbuka

Diberikan himpunan tak-kosong X, suatu koleksi $\tau$ yang berisikan himpunan-himpunan bagian dari X dikatakan topologi matematika pada X, jika ia memenuhi

X dan himpunan kosong $\emptyset$ termuat di dalam $\tau$ .
Sembarang gabungan (berhingga ataupun tak hingga) dari himpunan-himpunan di $\tau$ termuat di $\tau$ juga.
Irisan berhingga dari himpunan-himpunan di $\tau$ berada di $\tau$ juga.

Pasangan $\left(X,\tau \right)$ dikatakan ruang topologi, dengan koleksi $\tau$ disebut sebagai topologi pada X, serta anggota $\tau$ disebut sebagai himpunan terbuka dari X.

Definisi melalui himpunan tertutup

Menggunakan hukum de Morgan, aksioma-aksioma di atas yang menggunakan himpunan terbuka dapat diubah menjadi aksioma-aksioma menggunakan himpunan tertutup:

Himpunan kosong dan X merupakan himpunan tertutup.
Sembarang Irisan dari himpunan tertutup juga tertutup.
Gabungan berhingga dari himpunan-himpunan tertutup juga tertutup.

Menggunakan aksioma-aksioma ini topologi pada X ditentukan oleh koleksi $\tau$ keluarga subhimpunan tertutup dari X dengan komplemennya adalah himpunan terbuka.

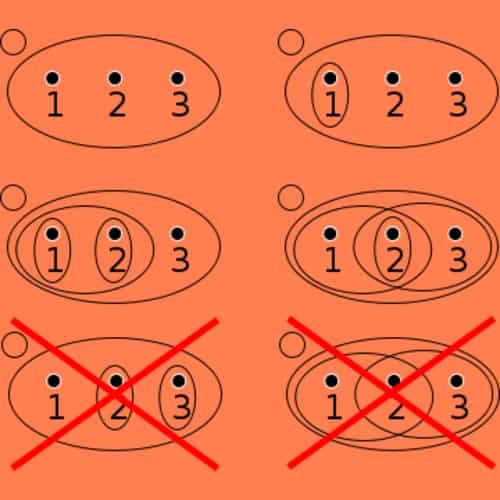
Contoh topologi matematika dan bukan — Empat contoh dan dua bukan-contoh topologi pada set tiga poin {1,2,3}. Contoh bawah-kiri bukan topologi karena penyatuan {2} dan {3} [yaitu {2,3}] hilang; contoh kanan bawah bukan merupakan topologi karena perpotongan {1,2} dan {2,3} [i.e. {2}], hilang. Sumber foto: Wikipedia

Contoh topologi matematika diskret

S = {1, 2, 3}, T = { $\varnothing$ , {1, 2, 3}}, T1 = $\varnothing$ , T2 = {1, 2, 3}, A = {1, 2}
(i) T1 $\cup$ T2 = {1, 2, 3} $\in$ T
(ii) T1 $\cap$ T2 = $\varnothing$ $\in$ T
(iii) $\varnothing$ $\in$ T, S $\in$ T

2. Homeomorfisme

Dalam bidang topologi, homeomorfisme atau isomorfisme topologi (dari bahasa Yunani, homeos = identik dan morphe = bentuk) adalah isomorfisme khusus antara ruang topologi yang memenuhi sifat-sifat topologi. Dua ruang dengan homeomorfisme antara mereka disebut homeomorfis. Dari tinjauan topologi mereka adalah sama.

Secara kasar dapat dikatakan, ruang topologi adalah objek geometri dan homeomorfisme adalah peregangan dan pembengkokan kontinu dari suatu objek menjadi objek bentuk baru. Jadi persegi dan lingkaran adalah homeomorfis. Dalam tinjauan topologi, cangkir bergagang satu dan kue donat adalah sama.

Sebuah fungsi $f:X\to Y$ antara dua ruang topologi $(X,{\mathcal {T}}_{X})$ dan $(Y,{\mathcal {T}}_{Y})$ disebut homeomorfisme jika memiliki sifat-sifat sebagai berikut:

$f$ adalah bijeksi (injektif dan surjektif),
$f$ adalah fungsi kontinu,
inversnya $f^{-1}$ kontinu. $f$ adalah pemetaan terbuka)

Fungsi dengan tiga sifat ini disebut juga dwikontinu. Jika terdapat fungsi dengan sifat-sifat tersebut, kita katakan $(X,{\mathcal {T}}_{X})$ dan $(Y,{\mathcal {T}}_{Y})$ adalah homeomorfik. Sebuah swahomeomorfisme atau otohomeomorfisme merupakan homeomorfisme dari sebuah ruang topologi ke dirinya sendiri. Homeomorfisme membentuk sebuah hubungan kesetaraan dalam sebuah kelas atau keluarga ruang topologi. Kelas kesetaraan ini disebut kelas homeomorfisme.

Contoh Homeomorfisme

Sebuah simpul trefoil homeomorfik dengan torus, tapi tidak isotopik (setara secara homotopi) di R³. Pemetaan kontinu tidak selalu bisa direalisasikan sebagai deformasi. Simpul ditebalkan untuk membuat gambar mudah dipahami.

Interval terbuka ${\textstyle (a,b)}$ homeomorfik dengan garis bilangan riil ${\textstyle \mathbf {R} }$ . (dalam kasus ini salah satu pemetaan bikontinu diberikan oleh ${\textstyle f(x)={\frac {1}{a-x}}+{\frac {1}{b-x}}}$ dimana pemetaan lain bisa juga diberikan oleh fungsi tan or arg tanh yang telah dibesar-kecilkan dan digeser).
Cakram satuan ${\textstyle D^{2}}$ dan persegi satuan (persegi dengan panjang sisi 1 dan isinya) di R² saling homeomorfik; karena cakram dan persegi bisa dideformasi satu sama lain. Salah satu contoh pemetaan dwikontinu dari persegi ke cakram diberikan oleh, dalam koordinat polar, $(\rho ,\theta )\mapsto \left(\rho \max(|\cos \theta |,|\sin \theta |),\theta \right)$ .
Kurva dari fungsi yang dapat diturunkan homeomorfik dengan domain fungsi itu sendiri.
Sebuah parametrisasi dari kurva merupakan homeomorfisme antara domain parametrisasi dan kurva tersebut.
Sebuah peta dari sebuah manifold adalah homeomorfisme antara himpunan terbuka dari manifold dengan sebuah himpunan terbuka dari ruang Euklides.
Proyeksi stereografik merupakan homeomorfisme antara kulit bola di R³ dengan salah satu titiknya dihilangkan, dengan seluruh titik di R².
Jika $G$ adalah sebuah grup topologis, peta inversinya $x\mapsto x^{-1}$ merupakan sebuah homeomorfisme. Juga, untuk sembarang $x\in G$ , pergeseran kiri $y\mapsto xy$ , pergeseran kanan $y\mapsto yx$ , dan otomorfisme dalamnya (transformasi konjugat) $y\mapsto xyx^{-1}$ merupakan homeomorfisme.

Contoh Soal Topologi Matematika

1. Diberikan $\tau=\phi, X,(a),(c,d),(a,c,d),(b,c,d,e)$ adalah suatu topologi pada $X={a,b,c,d,e}$

i. Ambil $A = {b,c,d}$ .

sehingga $A^c = {a,e}$

$int(A^c)=int({a,e})$

$={a}$

Jadi, $ext (A) = {a}$

2. Diberikan $X=\left\{ a,b,c,d,e,f\right\}$ dan $\tau_1=\left\{ X,\emptyset,\left\{ a\right\} ,\left\{ c,d\right\} ,\left\{ a,c,d\right\} ,\left\{ b,c,d,e,f\right\} \right\}$

maka $\tau_1$ merupakan topologi pada $X$ , karena memenuhi semua kondisi dari definisi 1

3. Diberikan $X=\left\{ a,b,c,d,e,f\right\}$ dan $\tau_{3}=\left\{ X,\emptyset,\left\{ a\right\} ,\left\{ f\right\} ,\left\{ a,f\right\} ,\left\{ a,c,f\right\} ,\left\{ b,c,d,e,f\right\} \right\}$

maka $\tau_{3}$ bukanlah topologi pada $X$ irisan $\left\{ a,c,f\right\} \cap\left\{ b,c,d,e,f\right\} =\left\{ c,f\right\}$ dua himpunan di $\tau_{3}$ tidak termuat di $\tau_{3}$ . Itu artinya $\tau_{3}$ tidak memenuhi kondisi (iii) pada definisi 1.

4. Diberikan $X=\left\{ a,b,c,d,e,\right\}$ dan $\tau_{2}=\left\{ X,\emptyset,\left\{ a\right\} ,\left\{ c,d\right\} ,\left\{ a,c,e\right\} ,\left\{ b,c,d\right\} \right\}$

maka $\tau_{2}$ bukanlah topologi pada $X$ karena gabungan $\left\{ c,d\right\} \cup\left\{ a,c,e\right\} =\left\{ a,c,d,e\right\}$ dua himpunan di $\tau_{2}$ tidak termuat di $\tau_{2}$ . Itu artinya $\tau_{2}$ tidak memenuhi kondisi (ii) pada definisi 1

5. Diberikan $\mathbb{N}$ himpunan bilangan asli dan $\tau_{4}$ memuat $\mathbb{N}$ , $\emptyset$ dan himpunan bagian berhingga dari $\mathbb{N}$ maka $\tau_{4}$ bukanlah topologi pada $\mathbb{N}$ . Karena gabungan tak hingga $\left\{ 2\right\} \cup\left\{ 3\right\} \cup\ldots\cup\left\{ n\right\} \cup\ldots=\left\{ 2,3,\ldots n\ldots\right\}$

dari himpunan-himpunan di $\tau_{4}$ tidak termuat di $\tau_{4}$ .Itu artinya $\tau_{4}$ tidak memenuhi kondisi (ii) pada definisi 1.

6. Misalkan N = { 1,2,3,…} dan M = { 2,4,6,…}

Fungsi F : N → M yang didefinisikan oleh f(x) = 2x yang berkorespondensi satu – satu. Maka N equivalend dengan M.

7. Suatu kalimat terbuka ?(?, ?) dimana ?(?, ?) bernilai benar atau salah untu sebarang pasangan terurut (?, ?) yang termuat di ? × ?. Maka kita sebut ? suatu relasi dari ? ke ? dan menyatakannya dengan ? = (?, ?, ?(?, ?)). Jika ?(?, ?) bernilai benar, kita tulis ???, dibaca “? berhubungan dengan ?”. Jika ?(?, ?) tidak benar, kita tulis ???, dibaca “? tidak berhubungan dengan ?”.

Misalkan ?1 = (?, ?, ?(?, ?)) dimana ? adalah himpunan dari kaum wanita, dan ? himpunan kaum pria, serta ?(?, ?) berbunyi “? adalah suami dari ?”. Maka ?1 adalah suatu relasi.
Misalkan ?2 = (?, ?, ?(?, ?)), dimana ? adalah bilangan-bilangan asli, dan ?(?, ?) berbunyi “? habis dibagi oleh ?”. Maka ?2 adalah relasi 3?2 21, 2?2 12, dan lain sebagainya. Definisi 0.2.4 (Himpunan Jawaban). Misalkan ? = (?, ?, ?(?, ?)) adalah suatu relasi himpunan jawaban ? ∗ dari relasi ? yang terdiri dari elemen (?, ?) dalam ? × ? untuk ?(?, ?) bernilai benar, dinotasikan ? ∗ = {(?, ?)|? ∈ ?, ? ∈ ?, ?(?, ?) adalah benar}.
Misalkan ? = (?, ?, ?(?, ?)) dimana ? = {2,3,4}, ? = {3,4,5,6} dan ?(?, ?) berbunyi “? habis dibagi oleh ?”. Maka himpunan jawabannya adalah ? ∗ = {(2,4), (2,6), (3,3), (3,6), (4,4)} Relasi sebagai himpunan dari pasangan-pasangan terurut.
Misalkan ? ∗ sebarang subset dari ? × ?, kita dapat mendefinisikan suatu relasi ? = (?, ?, ?(?, ?)) dimana ?(?, ?) berbunyi “Pasangan terurut (?, ?) termasuk ke dalam ?”.
Definisi: suatu relasi ? dari ? ke ? adalah himpunan dari ? × ?. Proposisi 0.2.7. Misalkan himpunan ? memiliki ? buah elemen, dan himpunan ? memiliki ? buah elemen, maka terdapat 2?? buah relasi dari ? ke ? yang berbeda.

8. Jika K = { k, o, m, p, a, s } dan L = { m, a, s, u, k }, maka K $\cup$ L = …

A. { p. o, s, u, k, m, a }
B. { m, a, s, b, u, k }
C. { p, a, k, u, m, i, s}
D. { k, a, m, p, u, s }
Pembahasan
K = { k, o, m, p, a, s }
L = { m, a, s, u, k }
K $\cup$ L = { k, o, m, p, a, s, u }

Diantara jawaban A, B, C dan D yang memiliki anggota K = anggota K $\cup$ L adalah opsi A
Kunci jawaban: A

9. Jika A = {0,1} maka n(A) =…

A. 0
B. 1
C. 2
D. 3

Pembahasan:
n(A) adalah simbol dari kardinalitas atau banyaknya anggota suatu himpunan. Jadi banyaknya anggota suatu himpunan dari himpunan A adalah 2, yaitu 0 dan 1.
Kunci jawaban: A

10. Diketahui K = { bilangan prima antara 2 dan 12} dan L = { 4 bilangan kelipatan 3 yang pertama}. $A\cap B$ adalah…

A. { 3,5,6,7,9,11,12}
B. { 5,6,7,9,11,12}
C. {3,6,9}
D. {3}

Pembahasan
K = { bilangan prima antara 2 dan 12}, maka K={3,5,7,11}
L = { 4 bilangan kelipatan 3 yang pertama}, maka L={3,6,9,12}
K $\cap$ L = {3}
Kunci jawaban: D

11. Jika himpunan $A\subset B$ dengan n(A) = 11 dan n(B) = 18 maka n ( $A\cap B$ ) =…

A. 7
B. 11
C. 18
D. 28

Pembahasan
n ( A ) = 11
n ( B ) = 18
Setiap $A\subset B$ maka $A\cap B$ = A
Sehingga n ( $A\cap B$ ) = n ( A )
n ( $A\cap B$ ) = 11
Kunci jawaban: B

12. Tuliskan anggota-anggota yang terdapat di dalam himpunan berikut.
a. P adalah himpunan nama presiden Republik Indonesia.
b. Q adalah himpunan bilangan genap yang kurang dari 10.
c. R adalah himpunan nama pulau besar di Indonesia.
d. S adalah himpunan faktor dari 36 yang kurang dari 20.
e. T adalah himpunan nama benua.
f. U adalah himpunan nama samudera.
g. V adalah himpunan nama bulan yang berjumlah 30 hari.
h. W adalah himpunan hewan pemakan rumput.
i. X adalah himpunan kendaraan beroda empat.
j. Y adalah himpunan nama hari yang diawali dengan huruf S.

Pembahasan:

a. P = {Sukarno, Suharto, B.J. Habibie, Abdurahman Wahid, Megawati
Sukarnoputri,Susilo Bambang Yudhoyono}.
b. Q = {2,4,6,8}
c. R = {Papua, Kalimantan,Sumatera, Sulawesi, Jawa}
d. S = {1,2,3,4,6,9,12,18}
e. T = {Asia, Afrika, Eropa, Amerika,Australia}
f. U = {Hindia, Pasifik, Atlantik,Artik}
g. V = {April, Juni, September, November}
h. W = { Sapi,Kuda, Kambing,Kerbau}
i. X = {Sedan, Truk, Bus}
j. Y = {Senin, Selasa, Sabtu}

Bacaan Lainnya

Sumber bacaan: Brilliant, Wayne State University, University of Waterloo, Britannica

Topologi Matematika – Contoh Soal dan Jawaban Ruang Topologi

Topologi Matematika

1. Topologi terhadap Himpunan

Secara formal, misalkan X sebuah himpunan dan τ adalah keluarga subhimpunan dari X. Maka τ disebut topologi terhadap X jika:

Definisi melalui hubungan ketetanggaan

Definisi melalui himpunan terbuka

Definisi melalui himpunan tertutup

2. Homeomorfisme

Contoh Homeomorfisme

Contoh Soal Topologi Matematika

1. Diberikan $\tau=\phi, X,(a),(c,d),(a,c,d),(b,c,d,e)$ adalah suatu topologi pada $X={a,b,c,d,e}$

2. Diberikan $X=\left\{ a,b,c,d,e,f\right\}$ dan $\tau_1=\left\{ X,\emptyset,\left\{ a\right\} ,\left\{ c,d\right\} ,\left\{ a,c,d\right\} ,\left\{ b,c,d,e,f\right\} \right\}$

3. Diberikan $X=\left\{ a,b,c,d,e,f\right\}$ dan $\tau_{3}=\left\{ X,\emptyset,\left\{ a\right\} ,\left\{ f\right\} ,\left\{ a,f\right\} ,\left\{ a,c,f\right\} ,\left\{ b,c,d,e,f\right\} \right\}$

4. Diberikan $X=\left\{ a,b,c,d,e,\right\}$ dan $\tau_{2}=\left\{ X,\emptyset,\left\{ a\right\} ,\left\{ c,d\right\} ,\left\{ a,c,e\right\} ,\left\{ b,c,d\right\} \right\}$

6. Misalkan N = { 1,2,3,…} dan M = { 2,4,6,…}

8. Jika K = { k, o, m, p, a, s } dan L = { m, a, s, u, k }, maka K $\cup$ L = …

9. Jika A = {0,1} maka n(A) =…

10. Diketahui K = { bilangan prima antara 2 dan 12} dan L = { 4 bilangan kelipatan 3 yang pertama}. $A\cap B$ adalah…

11. Jika himpunan $A\subset B$ dengan n(A) = 11 dan n(B) = 18 maka n ( $A\cap B$ ) =…

Bacaan Lainnya

Nilai Pi 1 juta digit pertama | Analisis dan…

Menghitung Dimensi Balok dari Luas Jaring-Jaringnya

Rumus Matematika dan Contoh untuk Penggunaan Sehari-hari

Tinggalkan Balasan Batalkan balasan

Topologi Matematika – Contoh Soal dan Jawaban Ruang Topologi

Topologi Matematika

1. Topologi terhadap Himpunan

Secara formal, misalkan X sebuah himpunan dan τ adalah keluarga subhimpunan dari X. Maka τ disebut topologi terhadap X jika:

Definisi melalui hubungan ketetanggaan

Definisi melalui himpunan terbuka

Definisi melalui himpunan tertutup

2. Homeomorfisme

Contoh Homeomorfisme

Contoh Soal Topologi Matematika

6. Misalkan N = { 1,2,3,…} dan M = { 2,4,6,…}

8. Jika K = { k, o, m, p, a, s } dan L = { m, a, s, u, k }, maka K <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e8ff7d0293ad19b43524a133ae5129f3d71f2040" alt="\cup " /> L = …

9. Jika A = {0,1} maka n(A) =…

10. Diketahui K = { bilangan prima antara 2 dan 12} dan L = { 4 bilangan kelipatan 3 yang pertama}. <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/bb27b38cf9eac6060e67b61f66cd9beec5067f81" alt="A\cap B" /> adalah…

Bacaan Lainnya

Nilai Pi 1 juta digit pertama | Analisis dan…

Menghitung Dimensi Balok dari Luas Jaring-Jaringnya

Rumus Matematika dan Contoh untuk Penggunaan Sehari-hari

Tinggalkan Balasan Batalkan balasan

8. Jika K = { k, o, m, p, a, s } dan L = { m, a, s, u, k }, maka K $\cup$ L = …

10. Diketahui K = { bilangan prima antara 2 dan 12} dan L = { 4 bilangan kelipatan 3 yang pertama}. $A\cap B$ adalah…