Pangkat Eksponen

Eksponensiasi atau pangkat eksponen adalah operasi matematika yang melibatkan dua bilangan:

Basis (bilangan pokok) = b
Eksponen (pangkat) = n

Ditulis sebagai: bⁿ

Artinya, b dikalikan dengan dirinya sendiri sebanyak n kali.

Ketika n adalah bilangan bulat positif, eksponensiasi adalah perkalian berulang dari basis: yaitu, bⁿ adalah produk dari mengalikan basis n:

b^{n}=\underbrace {b\times \cdots \times b} _{n}

Dalam kasus itu, bⁿ disebut pangkat n dari b, atau b dipangkatkan n.

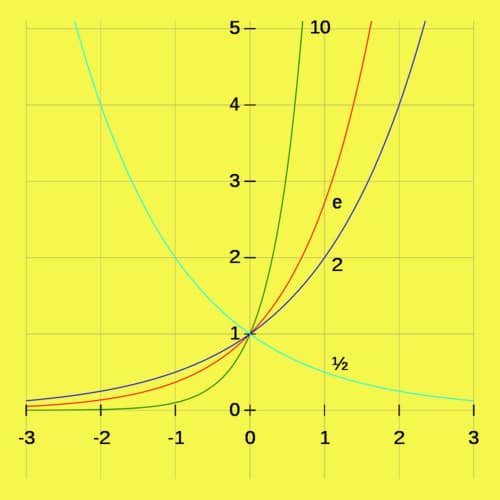
Rumus Pangkat Eksponen:

aⁿ = a × a × a × … × a (sebanyak n faktor)

Contoh Perhitungan:

3⁴ = 3 × 3 × 3 × 3 = 81

Penerapan Eksponensiasi:

Eksponen digunakan dalam berbagai bidang, seperti:
✅ Ekonomi → Perhitungan bunga berbunga
✅ Biologi → Model pertumbuhan populasi
✅ Fisika → Perilaku gelombang & energi
✅ Kimia → Kinetika reaksi kimia
✅ Ilmu komputer → Kriptografi & algoritma komputasi

🚀 Eksponensiasi adalah dasar dari banyak konsep penting dalam sains dan teknologi!

Pangkat Eksponen nol

Jika a ≠ 0 maka a⁰ = 1
contoh
2⁰ =1
3⁰ =1
128384⁰ =1
x⁰ =1

Pangkat Eksponen negatif dan pecahan

Jika m dan n adalah bilangan bulat positif maka
(i) a^-n = 1/aⁿ
contoh
2^-3= 1/2³ = 1/8
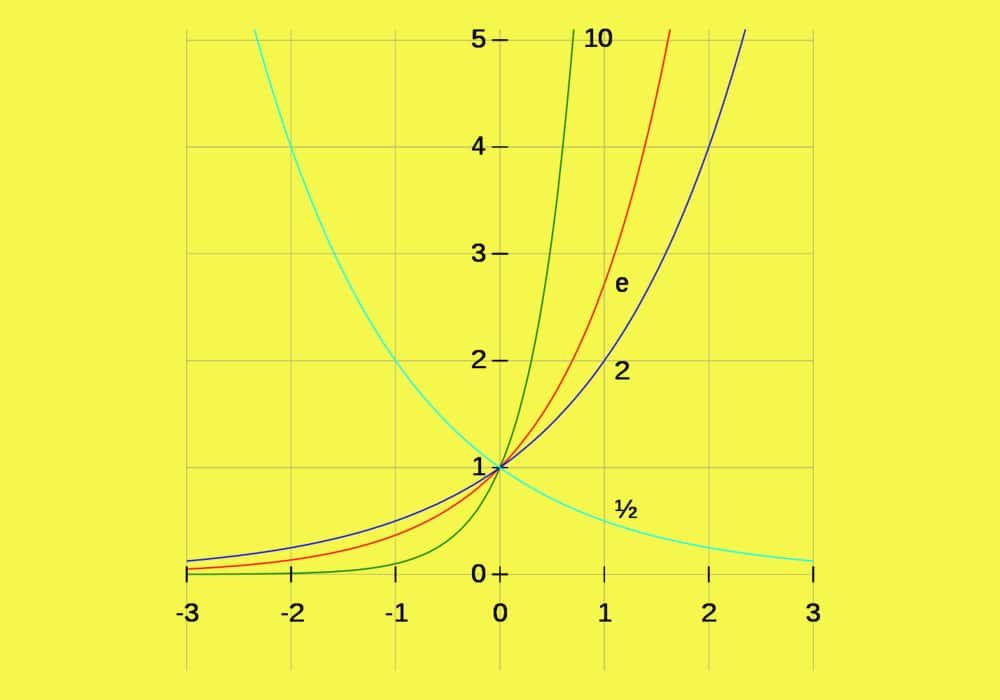
(ii) a^1/n = ⁿ√a
contoh
2^1/2 = √2
2^1/3 = ³√2

Bentuk Persamaan Eksponen

1. a^f(x)= 1 ( Jika a^f(x)= 1 dengan a>0 dan a ≠0, maka f(x) = 0 )
2. a^f(x)= a^p ( Jika a^f(x)= a^p dengan a>0 dan a ≠0, maka f(x) = p )
3. a^f(x)= a^g(x)( Jika a^f(x)= a^g(x) dengan a>0 dan a ≠0, maka f(x) = g(x) )
4. a^f(x)= b^f(x)( Jika a^f(x)= b^f(x) dengan a>0 dan a ≠1, b>0 dan b ≠1, dan a≠b maka f(x) = 0 )
5. A(a^f(x))² + B(a^f(x)) + C = 0 ( Dengan a^f(x) = p, maka bentuk persamaan diatas dapat diubah menjadi persamaan kuadrat : Ap² + Bp + C = 0 )

Latar Belakang Ekpresi Pangkat Eksponen

Eksponen menunjukkan berapa kali basis dikalikan dengan dirinya sendiri.

b² = b × b disebut “b kuadrat” (square) karena merepresentasikan luas bujursangkar dengan sisi b.
b³ = b × b × b disebut “b pangkat tiga” (cube) karena merepresentasikan volume kubus dengan sisi b.

Contoh Perhitungan Eksponen:

3⁵ = 3 × 3 × 3 × 3 × 3 = 243

Basis = 3
Eksponen = 5
Hasil = 243 atau disebut “3 pangkat lima” (three to the power of five).

Sejarah Eksponen & Notasi Modern

Kata “eksponen” diperkenalkan oleh Michael Stifel pada tahun 1544.
Notasi eksponensiasi modern diperkenalkan oleh René Descartes dalam Géométrie (1637).

🚀 Eksponen adalah dasar penting dalam matematika, digunakan dalam fisika, ekonomi, dan ilmu komputer!

Pangkat Eksponen integer

Bilangan $x$ disebut bilangan pokok, dan bilangan $y$ disebut eksponen. Sebagai contoh, pada $2^3$ , 2 adalah bilangan pokok dan 3 eksponen.

Untuk menghitung $2^3$ seseorang harus mengalikan 3 kali terhadap angka 2. Sehingga $2^{3}=2\cdot 2\cdot 2$ . Hasilnya adalah $2\cdot 2\cdot 2=8$ . Apa yang dikatakan persamaan bisa juga dikatakan dengan cara ini: 2 pangkat 3 sama dengan 8.

Contoh:

$5^{3}=5\cdot {}5\cdot {}5=125$
$x^{2}=x\cdot {}x$
$1^{x}=1$ untuk setiap bilangan x

Jika eksponen sama dengan 2, maka disebut persegi karena area persegi dihitung menggunakan $a^{2}$ . Sehingga

x^{2}

adalah persegi dari

x

Jika eksponen sama dengan 3, maka disebut kubik karena volume kubus dihitung dengan $a^{3}$ . Sehingga

x^{3}

adalah kubik

x

Jika eksponen sama dengan -1 orang harus menghitung invers bilangan pokok. Sehingga: $x^{-1}={\frac {1}{x}}$ Jika eksponen adalah integral dan kurang dari 0, orang harus membalik bilangan dan menghitung pangkat. Sebagai contoh:

2^{-3}=({\frac {1}{2}})^{3}={\frac {1}{8}}

Jika eksponen sama dengan ${\frac {1}{2}}$ hasilnya adalah akar persegi (akar kuadrat) bilangan pokok. Sehingga $x^{\frac {1}{2}}={\sqrt {x}}.$ Contoh:

4^{\frac {1}{2}}={\sqrt {4}}=2

Dengan cara yang sama, jika eksponen ${\frac {1}{n}}$ hasilnya adalah akar ke-n, sehingga:

a^{\frac {1}{n}}={\sqrt[{n}]{a}}

Jika eksponen merupakan bilangan rasional ${\frac {p}{q}}$ , hasilnya adalah akar ke-q bilangan pokok yang dipangkatkan p, sehingga:

a^{\frac {p}{q}}={\sqrt[{q}]{a^{p}}}

Eksponen bisa juga tak rasional. Untuk menjadikan bilangan pokok a menjadi pangkat ke-x yang tak rasional, kita menggunakan rangkaian ketidakterhinggaan bilangan rasional (x_i), yang limitnya adalah x:

x=\lim _{n\to \infty }x_{n}

seperti ini: $a^{x}=\lim _{n\to \infty }a^{x_{n}}$

Ada beberapa aturan yang membantu menghitung pangkat:

$\left(a\cdot b\right)^{n}=a^{n}\cdot {}b^{n}$
$\left({\frac {a}{b}}\right)^{n}={\frac {a^{n}}{b^{n}}},\quad b\neq 0$
$a^{r}\cdot {}a^{s}=a^{r+s}$
${\frac {a^{r}}{a^{s}}}=a^{r-s},\quad a\neq 0$
$a^{-n}={\frac {1}{a^{n}}},\quad a\neq 0$
$\left(a^{r}\right)^{s}=a^{r\cdot s}$
$a^{0}=1,\quad a\neq 0$ : Bila bilangan pokok lebih besar daripada 1 dan eksponen 0, jawabannya 1. Jika bilangan pokok dan pangkat sama dengan 0, jawabannya tak terdefinisikan.

Ekponen matriks bisa pula dihitung. Matriks itu harus persegi. Sebagai contoh: $I^{2}=I\cdot I=I$ .

Daftar eksponensial bilangan bulat

n	n²	n³	n⁴	n⁵	n⁶	n⁷	n⁸	n⁹	n¹⁰
2	4	8	16	32	64	128	256	512	1,024
3	9	27	81	243	729	2,187	6,561	19,683	59,049
4	16	64	256	1,024	4,096	16,384	65,536	262,144	1,048,576
5	25	125	625	3,125	15,625	78,125	390,625	1,953,125	9,765,625
6	36	216	1,296	7,776	46,656	279,936	1,679,616	10,077,696	60,466,176
7	49	343	2,401	16,807	117,649	823,543	5,764,801	40,353,607	282,475,249
8	64	512	4,096	32,768	262,144	2,097,152	16,777,216	134,217,728	1,073,741,824
9	81	729	6,561	59,049	531,441	4,782,969	43,046,721	387,420,489	3,486,784,401
10	100	1,000	10,000	100,000	1,000,000	10,000,000	100,000,000	1,000,000,000	10,000,000,000

Contoh Soal dan Jawaban Pangkat Exponen

Contoh Soal Persamaan Pangkat Eksponen Bentuk a^f(x) = 1

Tentukan himpunan penyelesaian dari:

- 3 ^5x-10= 1

2 ^2x²+3x-5= 1

Jawaban:

3 ^5x-10 = 1

3 ^5x-10 = 3⁰5x-10 = 0
5x = 10
x = 2

2 ^2x²+3x-5= 1

2 ^2x²+3x-5 = 2⁰2x²+2x-5 = 0
(2x+5) (x-1) = 0
2x+5 = 0 | x-1 = 0
X = -²⁄₅ | x = 1

Contoh Soal Persamaan Pangkat Eksponen Bentuk a^f(x)= a^p

Tentukan himpunan penyelesaian dari:

- 5 ^2x-1= 625

- 2 ^2x-7= ⅓₂

√3^3x-10= ½₇√3

Jawaban:

5 ^2x-1= 625

5 ^2x-1 = 5⁴2x-1 = 4
2x = 4+1
2x = 5
x= 5/2

Alternatif: x= 2 ½, x= 2,5

2 ^2x-7= ⅓₂

2 ^2x-7 = 2^-52x-7 = -5
2x = 2
x = 1

√3^3x-10= ½₇√3

3^3x-10⁄2 = 3^-3.3^½3^3x-10⁄2 = 3^-⁵⁄₂3x-10⁄2 = -⁵⁄₂
3x-10     = -5
3x           = 5
x             = ⁵⁄₃

Contoh Persamaan Pangkat Eksponen Bentuk a^f(x)= a^g(x)

Tentukan himpunan penyelesaian dari:

- 9 ^x²+x= 27 ^x²-1

25 ^x+2= (0,2) ^1-x

Jawaban:

9 ^x²+x= 27 ^x²-1

3 ^2(x²+x) = 3 ^3(x²-1)

2 (x²+x) = 3 (x²-1)

2x² + 2x = 3x² – 3

x² – 2x – 3 = 0

(x – 3) (x + 1) = 0

x = 3 x = -1 Jadi HP = { –1,3 }

25 ^x+2= (0,2) ^1-x

5^2(x+2) = 5 ^-1(1-x)

2x + 4 = -1 + x

2x – x = -1 – 4

x = -5 Jadi HP = { -5 }

Contoh Persamaan Eksponen Bentuk A(a^f(x))²+ B(a^f(x)) + C

Tentukan himpunan penyelesaian dari: 2^2x– 2^x+3 + 16 = 0

Jawaban:

2^2x– 2^x+3 + 16 = 0
2^2x – 2^x.2³ + 16 = 0

Misalkan 2^x = p, maka persamaannya menjadi

P² – 8p + 16 = 0
(p-4) p-4) = 0
p = 4

Untuk p = 4, jadi

2^x = 4
2^x = 2²x = 2
Jadi HP = { 2 }

Contoh Persamaan Pangkat Eksponen Bentuk a^f(x)= b^f(x)

Tentukan himpunan penyelesaian dari :

- 6 ^x-3= 9 ^x-3

7^x²-5x+6= 8^x²-5x+6

Jawaban:

6 ^x-3= 9 ^x-3

x-3 = 0
x = 3
Jadi HP = { 3 }

7^x²-5x+6= 8^x²-5x+6

x²-5x+6 = 0
(x-6) (x+1) = 0
x = 6 x = -1
Jadi HP = { -1,6 }

Jika x₁.x₂ adalah akar-akar 25^2x – 5^2x+1 – 2.5^2x+3 + a = 0 dimana x₁ + x₂ = 2.⁵log 2, maka a =

$\displaystyle \begin{aligned} 25^{2x}-5^{2x+1}-2\cdot 5^{2x+3}+a&=0\\ (25^x)^2-5\cdot 25^x -2\cdot 125\cdot 25^x + a &=0\\ (25^x)^2-255\cdot 25^x+a&=0 \end{aligned}$

Persamaan terakhir bisa diperlakukan seperti persamaan kuadrat dimana 25^x₁ dan 25^x₂ adalah akar-akar persamaan kuadrat tersebut.
Diketahui dari soal x₁+x₂ = 2.⁵log 2 → x₁+x₂ = ⁵log 4.

$\displaystyle \begin{aligned} 25^{x_1}\cdot 25^{x_2} &= a\\ 25^{x_1+x_2}&=a\\ 25^{\;^5\!\log 4} &= a\\ \left(5\;^{^5\log 4}\right)^2&=a\\ 4^2&=a\\ \therefore \:a&=16 \end{aligned}$

catatan:
Jika x₁ dan x_{2 adalah akar-akar dari ax² + bx + c = 0}

$\boxed{~a^m\cdot a^n = a^{m+n}~}$

$\boxed{~(a^m)^n=(a^n)^m=a^{mn}~}$

$\boxed{~a^{^a\!\log b}=b~}$

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Rapid Tables, Purple Math

Pangkat Eksponen – Integer – Daftar eksponensial bilangan bulat dan contoh soal dan jawaban