Kecepatan Cahaya
Laju kecepatan cahaya (kelajuan cahaya dalam ruang vakum; kecepatan cahaya), disimbolkan dengan c, adalah sebuah konstanta fisika universal yang penting dalam banyak bidang fisika. Nilai presisi kecepatan cahaya adalah 299 792 458 meter per detik (kira-kira 3.00×108 m/s), karena panjang meter didefinisikan berdasarkan konstanta ini dan standar internasional waktu.
Nilai numerik, notasi dan unit kecepatan cahaya
Laju cahaya dalam ruang hampa biasanya dilambangkan dengan huruf kecil c, untuk “constant” atau bahasa Latin celeritas (yang berarti “kecepatan”). Secara historis, simbol V pernah digunakan sebagai simbol alternatif untuk laju cahaya, yang diperkenalkan oleh James Clerk Maxwell pada tahun 1865.
Pada tahun 1856, Wilhelm Eduard Weber dan Rudolf Kohlrausch telah menggunakan c untuk konstanta yang berbeda yang kemudian terbukti sama dengan √2 dikalikan laju cahaya dalam ruang hampa.
Pada tahun 1894, Paul Drude mendefinisikan ulang c dengan makna modern. Einstein menggunakan V di makalah asli berbahasa Jerman tentang relativitas khusus pada tahun 1905. Namun pada tahun 1907 ia beralih ke c, yang saat itu telah menjadi simbol standar untuk laju cahaya.
Kadang-kadang c digunakan untuk laju gelombang di medium bahan apapun, dan c0 untuk laju cahaya dalam ruang hampa. Notasi subscript ini, yang didukung dalam literatur SI resmi, memiliki bentuk yang sama sebagai konstanta terkait lainnya:
yaitu, μ0 untuk permeabilitas vakum atau konstanta magnetik.
ε0 untuk permitivitas vakum atau konstanta listrik.
Z0 untuk impedansi ruang hampa. Artikel ini menggunakan ceksklusif untuk kecepatan cahaya dalam ruang hampa.
Sejak tahun 1983, meter telah didefinisikan dalam Sistem Satuan Internasional (SI) sebagai jarak perjalanan cahaya dalam ruang hampa dalam 1⁄299792458 detik. Definisi ini menetapkan laju cahaya dalam ruang hampa di persis 299792458 m/s.
Sebagai sebuah konstanta fisika berdimensi, nilai numerik dari c berbeda untuk sistem unit yang berbeda. Dalam cabang fisika di mana c sering muncul, seperti dalam relativitas, itu adalah umum untuk menggunakan sistem pengukuran satuan natural atau sistem unit tergeometrisasi dengan c = 1.
Menggunakan unit-unit ini, c tidak muncul secara eksplisit karena perkalian atau pembagian dengan 1 tidak memengaruhi hasil.
Peran kecepatan cahaya fundamental dalam fisika
Kelajuan di mana gelombang cahaya merambat dalam ruang hampa adalah independen baik dari gerakan sumber gelombang dan dari kerangka acuan inersial pengamat.
Invariansi dari kecepatan cahaya ini didalilkan oleh Einstein pada tahun 1905, setelah termotivasi oleh teori elektromagnetik Maxwell dan kurangnya bukti untuk luminiferous aether; sejak saat itu telah secara konsisten dikonfirmasi oleh banyak percobaan.
Hal ini hanya mungkin untuk memverifikasi secara eksperimental bahwa laju cahaya dua arah (misalnya, dari sumber ke cermin dan kembali lagi) adalah independen-kerangka, karena tidak mungkin untuk mengukur laju cahaya satu arah (misalnya, dari sumber ke detektor yang jauh) tanpa beberapa konvensi bagaimana jam pada sumber dan pada detektor harus disinkronkan.
Namun, dengan mengadopsi sinkronisasi Einstein untuk jam, kecepatan satu arah cahaya menjadi sama dengan kecepatan dua arah cahaya dengan definisi.
Teori relativitas khusus mengeksplorasi konsekuensi dari invariansi c dengan asumsi bahwa hukum fisika adalah sama dalam semua kerangka acuan inersial.
Salah satu konsekuensi adalah bahwa c adalah laju di mana semua partikel tak bermassa dan gelombang, termasuk cahaya, harus berjalan dalam ruang hampa.
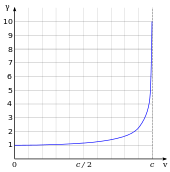
Faktor Lorentz γ sebagai fungsi dari kecepatan. Dimulai pada 1 dan mendekati tak terhingga sebagai vmendekati c.
Relativitas khusus memiliki banyak implikasi yang berlawanan dengan intuisi dan diverifikasi secara eksperimental. Ini termasuk kesetaraan massa dan energi (E = mc2), kontraksi panjang (benda bergerak menjadi lebih pendek) dan dilatasi waktu (jam bergerak berjalan lebih lambat).
Faktor γ oleh yang panjang berkontraksi dan waktu berdilatasi dikenal sebagai faktor Lorentz dan diberikan oleh γ = (1 − v2/c2)−1/2, di mana v adalah kelajuan benda.
Perbedaan γ dari 1 dapat diabaikan untuk kelajuan jauh lebih lambat dari c, seperti kebanyakan kecepatan sehari-hari—tempat relativitas khusus didekati oleh relativitas Galilea-tetapi meningkat pada kecepatan relativistik dan menyimpang hingga tak terbatas ketika vmendekati c.
Hasil relativitas khusus dapat diringkas dengan memperlakukan ruang dan waktu sebagai struktur terpadu yang dikenal sebagai ruang-waktu (dengan c mengaitkan unit ruang dan waktu), dan mengharuskan teori fisika memenuhi simetri khusus yang disebut invariansi Lorentz, yaitu formulasi matematis berisi parameter c.
Invariasi Lorentz adalah asumsi hampir universal untuk teori fisika modern, seperti:
Elektrodinamika kuantum.
Kromodinamika kuantum.
Model Standar fisika partikel.
Relativitas umum.
Dengan demikian, parameter c ada di mana-mana dalam fisika modern, muncul dalam banyak konteks yang tidak berhubungan dengan cahaya. Misalnya, relativitas umum memprediksi bahwa c juga merupakan kelajuan gravitasi dan gelombang gravitasi.
Pada kerangka acuan non-inersial (ruang gravitasi melengkung atau kerangka acuan dipercepat), laju lokal cahaya adalah konstan dan sama dengan c, tetapi laju cahaya di sepanjang lintasan panjang yang terbatas dapat berbeda dari c, tergantung pada bagaimana jarak dan waktu ditentukan.
Secara umum diasumsikan bahwa konstanta fundamental seperti c memiliki nilai yang sama di seluruh ruang-waktu, yang berarti bahwa mereka tidak bergantung pada lokasi dan tidak bervariasi dengan waktu. Namun, telah disarankan dalam berbagai teori bahwa laju cahaya mungkin telah berubah dari waktu ke waktu.
Tidak ada bukti konklusif untuk perubahan tersebut yang telah ditemukan, tetapi hal itu tetap menjadi subjek penelitian yang sedang berlangsung.
Umumnya juga diasumsikan bahwa kecepatan cahaya adalah isotropik, yang berarti bahwa ia memiliki nilai yang sama tidak bergantung arah di mana itu diukur.
Pengamatan dari emisi dari tingkat energi nuklir sebagai fungsi orientasi inti yang memancarkan emisi dalam medan magnet (lihat percobaan Hughes-Drever) dan resonator optik berputar (lihat percobaan resonator) telah memberi batas ketat pada kemungkinan anisotropi dua arah.
Batas atas kelajuan kecepatan cahaya
Menurut relativitas khusus, energi dari suatu objek dengan massa diam m dan kelajuan v diberikan oleh γmc2, di mana γ adalah faktor Lorentz didefinisikan di atas.
Ketika v adalah nol, γ sama dengan satu, sehingga menimbulkan rumus terkenal E = mc2 untuk kesetaraan massa-energi.
Faktor γ mendekati tak terhingga sebagai v mendekati c, dan itu akan mengambil jumlah tak terbatas energi untuk mempercepat objek dengan massa untuk laju cahaya.
Laju cahaya adalah batas atas untuk kelajuan benda dengan massa diam positif, dan foton individu tidak dapat melakukan perjalanan lebih cepat dari laju cahaya. Ini secara eksperimental dibuktikan di banyak uji energi relativistik dan momentum.
Pada umumnya dan biasanya tidak mungkin untuk informasi atau energi untuk melakukan perjalanan lebih cepat dari c. Salah satu argumen untuk ini mengikuti dari implikasi kontra-intuitif relativitas khusus yang dikenal sebagai relativitas simultanitas.
Jika jarak spasial antara dua peristiwa A dan B lebih besar dari interval waktu antara mereka dikalikan dengan c maka ada kerangka acuan di mana A mendahului B, yang lain di mana B mendahului A, dan yang lain di mana mereka simultan.
Akibatnya, jika sesuatu bepergian lebih cepat dari c relatif terhadap sebuah kerangka acuan inersial, itu akan menjadi perjalanan mundur dalam waktu relatif terhadap bingkai lain, dan kausalitas akan dilanggar.
Dalam kerangka acuan ini, sebuah “akibat” bisa diamati sebelum “penyebab”-nya. Pelanggaran kausalitas seperti itu tidak pernah direkam dan akan menyebabkan paradoks seperti antitelepon takion.
Pengamatan dan eksperimen lebih cepat-dari-cahaya
Ada situasi di mana mungkin tampak bahwa materi, energi, atau informasi bergerak pada laju lebih besar dari c, tetapi sebenarnya tidak. Misalnya, seperti yang dibahas dalam bagian perambatan cahaya di sebuah medium di bawah, banyak kecepatan gelombang dapat melebihi c.
Misalnya, kecepatan fase sinar-X melalui sebagian besar kaca secara rutin dapat melebihi c, tetapi kecepatan fase tidak menentukan kecepatan di mana gelombang menyampaikan informasi.
Jika sinar laser menyapu cepat di sebuah objek yang jauh, tempat cahaya dapat bergerak lebih cepat dari c. Meskipun gerakan awal tempat tertunda karena waktu yang dibutuhkan cahaya untuk sampai ke objek yang jauh dengan kelajuanc.
Namun, satu-satunya entitas fisik yang bergerak adalah laser dan cahaya yang dipancarkan, yang pada kelajuan c dari laser ke berbagai posisi dari tempat.
Demikian pula, bayangan diproyeksikan ke sebuah objek yang jauh dapat dibuat untuk bergerak lebih cepat dari c, setelah penundaan dalam waktu. Dalam hal yang manapun tidak ada materi, energi atau informasi yang bergerak lebih cepat dari cahaya.
Tingkat perubahan dalam jarak antara dua objek dalam suatu kerangka acuan terhadap yang keduanya bergerak (kelajuan penutupan mereka) mungkin memiliki nilai lebih dari c. Namun, ini tidak mewakili kecepatan dari setiap objek tunggal yang diukur dalam kerangka inersia tunggal.
Efek kuantum tertentu tampaknya ditularkan secara instan dan karena itu lebih cepat dari c, seperti dalam paradoks EPR. Contoh melibatkan keadaan kuantum dari dua partikel yang dapat terjerat. Sampai salah satu partikel yang diamati, mereka ada dalam superposisi dari dua keadaan kuantum.
Jika partikel dipisahkan dan keadaan kuantum satu partikel diamati, keadaan kuantum partikel lain ditentukan seketika (yaitu, lebih cepat dari cahaya bisa bepergian dari satu partikel ke yang lain).
Namun, tidak mungkin untuk mengontrol keadaan kuantum partikel pertama akan mengambil ketika diamati, sehingga informasi tidak dapat dikirimkan dengan cara ini.
Efek kuantum lain yang memprediksi terjadinya kelajuan lebih cepat dari cahaya disebut efek Hartman; dalam kondisi tertentu waktu yang diperlukan untuk sebuah partikel virtual untuk menerowong melalui penghalang adalah konstan, terlepas dari ketebalan penghalang. Hal ini dapat mengakibatkan partikel virtual melintasi jarak yang besar lebih cepat dari cahaya. Namun, tidak ada informasi yang dapat dikirim dengan efek ini.
Gerak superluminal terlihat di objek astronomi tertentu, seperti jet relativistik galaksi radio dan kuasar. Namun, jet ini tidak bergerak dengan kelajuan lebih dari laju cahaya: gerakan superluminal yang tampak adalah efek proyeksi yang disebabkan oleh benda yang bergerak mendekati laju cahaya dan mendekati Bumi pada sudut kecil dengan garis pandang:
Karena cahaya yang dipancarkan ketika jet itu lebih jauh membutuhkan waktu lebih lama untuk mencapai Bumi.
Waktu antara dua pengamatan berturut-turut sesuai dengan waktu yang lebih lama antara instan di mana sinar cahaya dipancarkan.
Dalam model alam semesta yang mengembang, semakin jauh galaksi dari satu sama lain, semakin cepat mereka menjauh. Kemunduran ini bukan karena gerakan melalui ruang, melainkan karena perluasan ruang itu sendiri.
Misalnya, galaksi yang jauh dari Bumi tampaknya bergerak menjauh dari Bumi dengan kelajuan sebanding dengan jarak mereka. Melampaui batas yang disebut bola Hubble, tingkat di mana jarak mereka dari Bumi meningkat menjadi lebih besar dari laju cahaya.
Persamaan perambatan cahaya
Dalam fisika klasik, cahaya dideskripsikan sebagai jenis gelombang elektromagnetik. Perilaku klasik medan elektromagnetik dijelaskan oleh persamaan Maxwell. Maxwell yang memprediksi bahwa kelajuan c di mana gelombang elektromagnetik (seperti cahaya) menyebar melalui vakum terkait dengan konstanta listrik ε0 dan konstanta magnetik μ0 dengan persamaan:
Dalam fisika kuantum modern, medan elektromagnetik dijelaskan oleh teori elektrodinamika kuantum (quantum electrodynamics, QED). Dalam teori ini, cahaya dideskripsikan oleh eksitasi mendasar (atau kuanta) dari medan elektromagnetik, yang disebut foton.
Dalam QED, foton adalah partikel tak bermassa dan dengan demikian, menurut relativitas khusus, mereka melakukan perjalanan dengan laju cahaya dalam ruang hampa.
Ekstensi dari QED di mana foton memiliki massa telah dipertimbangkan. Dalam teori semacam itu, kecepatannya akan tergantung pada frekuensi, dan kelajuan invarian c relativitas khusus maka akan menjadi batas atas laju cahaya dalam ruang hampa.
Tidak ada variasi laju cahaya dengan frekuensi telah diamati dalam pengujian ketat, menempatkan batas yang ketat pada massa foton. Batas diperoleh tergantung pada model yang digunakan:
Jika foton masif dijelaskan oleh teori Proca, batas atas eksperimental untuk massa adalah sekitar 10−57 gram.
Jika massa foton dihasilkan oleh mekanisme Higgs, batas atas eksperimental kurang tajam, m ≤ 10−14 eV/c2 (kira-kira 2 × 10−47 g).
Alasan lain untuk kecepatan cahaya bervariasi dengan frekuensi akan menjadi kegagalan relativitas khusus berlaku untuk skala kecil, seperti yang diperkirakan oleh beberapa teori yang diusulkan dari gravitasi kuantum.
Pada tahun 2009, pengamatan spektrum semburan sinar gamma GRB 090510 tidak menemukan perbedaan dalam kecepatan foton dengan energi yang berbeda, membenarkan bahwa invariansi Lorentz diverifikasi setidaknya sampai ke skala panjang Planck (lP = √ħG/c3 ≈ 1.6163×10−35 m) dibagi dengan 1,2.
Kecepatan cahaya di sebuah medium
Dalam sebuah medium, cahaya biasanya tidak bergerak pada laju yang sama dengan c; berbagai jenis gelombang cahaya akan melakukan perjalanan pada kelajuan yang berbeda.
Kelajuan di mana puncak-puncak individu dan palung dari gelombang bidang (gelombang mengisi seluruh ruang, dengan hanya satu frekuensi) merambat disebut kecepatan fase vp.
Sinyal fisik dengan batas terbatas (pulsa cahaya) bergerak pada kelajuan yang berbeda. Bagian terbesar dari pulsa berjalan pada kecepatan kelompok vg, dan bagian paling awal berjalan di kecepatan depan vf.
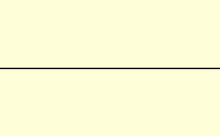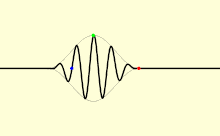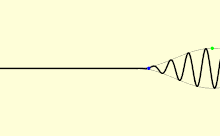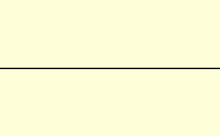
Kecepatan fase penting dalam menentukan bagaimana gelombang cahaya bergerak melalui materi atau dari satu material yang lain. Hal ini sering diwakili dalam hal indeks bias. Indeks bias material didefinisikan sebagai rasio c ke kecepatan fase vp dalam materi: indeks bias lebih besar menunjukkan kelajuan yang lebih rendah.
Indeks bias material mungkin tergantung pada frekuensi, intensitas, polarisasi, atau arah perambatan cahaya; meskipun, dalam banyak kasus, itu dapat diperlakukan sebagai konstanta bergantung-bahan. Indeks bias udara adalah sekitar 1,0003.
Media yang lebih padat, seperti air, kaca dan intan, memiliki indeks bias sekitar 1,3, 1,5 dan 2,4, secara berurutan, untuk cahaya tampak. Dalam bahan eksotis seperti kondensat Bose-Einstein dekat nol mutlak, laju efektif cahaya mungkin hanya beberapa meter per detik.
Namun, ini merupakan penundaan penyerapan dan re-radiasi antara atom, seperti semua kelajuan lebih lambat dari c dalam zat materi.
Sebagai contoh ekstrem dari “perlambatan” cahaya dalam materi, 2 tim independen dari fisikawan mengaku menjadikan cahaya “berhenti sepenuhnya” dengan melewatkannya melalui kondensat Bose-Einstein dari unsur rubidium, satu tim di Universitas Harvard dan Rowland Institute for Science di Cambridge, Mass., dan yang lainnya di Harvard-Smithsonian Center for Astrophysics, juga di Cambridge.
Namun, deskripsi populer cahaya “berhenti” dalam percobaan ini hanya mengacu pada cahaya yang disimpan dalam keadaan tereksitasi dari atom, kemudian kembali dipancarkan pada waktu kemudian, karena dirangsang oleh pulsa laser kedua. Selama “berhenti,” hal itu tidak lagi menjadi cahaya. Jenis perilaku ini umumnya benar secara mikroskopis di semua media transparan yang “memperlambat” laju cahaya.
Dalam bahan transparan, indeks bias umumnya lebih besar dari 1, berarti bahwa kecepatan fase kurang dari c. Dalam bahan lain, adalah mungkin untuk indeks bias menjadi lebih kecil dari 1 untuk beberapa frekuensi; di beberapa bahan eksotis bahkan dimungkinkan untuk indeks bias menjadi negatif.
Persyaratan bahwa kausalitas tidak dilanggar menyiratkan bahwa bagian real dan imajiner dari konstanta dielektrik dari bahan apapun, sesuai masing-masing dengan indeks bias dan dengan koefisien atenuasi, dihubungkan oleh hubungan Kramer-Kronig.
Secara praktis, ini berarti bahwa dalam bahan dengan indeks bias kurang dari 1, penyerapan gelombang sangat cepat yang tidak ada sinyal dapat dikirim lebih cepat dari c.
Sebuah pulsa dengan kecepatan kelompok dan fase yang berbeda (yang terjadi jika kecepatan fase tidak sama untuk semua frekuensi pulsa) menyebar dari waktu ke waktu, sebuah proses yang dikenal sebagai dispersi.
Bahan-bahan tertentu memiliki kecepatan kelompok yang sangat rendah (atau bahkan nol) untuk gelombang cahaya, fenomena yang disebut cahaya lambat, yang telah dikonfirmasi di berbagai eksperimen.
Sebaliknya, kecepatan kelompok melebihi c, juga telah ditunjukkan dalam percobaan. Bahkan mungkin untuk kecepatan kelompok menjadi tak terhingga atau negatif, dengan pulsa bepergian instan atau mundur dalam waktu.
Tak satu pun dari pilihan ini, bagaimanapun, memungkinkan informasi yang akan dikirim lebih cepat dari c. Tidak mungkin untuk mengirimkan informasi dengan pulsa cahaya lebih cepat dari kecepatan bagian awal dari pulsa (kecepatan depan). Hal ini dapat menunjukkan bahwa ini adalah (di bawah asumsi tertentu) selalu sama dengan c.
Hal ini dimungkinkan untuk partikel untuk melakukan perjalanan melalui media lebih cepat dari kecepatan fase cahaya dalam medium (tetapi masih lebih lambat dari c). Ketika partikel bermuatan melakukan itu dalam bahan dielektrik, ekuivalen elektromagnetik dengan gelombang kejut, dikenal sebagai radiasi Cherenkov, dipancarkan.
Efek praktis dari keterbatasan
Laju cahaya adalah relevan untuk komunikasi: waktu tunda pulang-pergi dan satu arah lebih besar dari nol. Hal ini berlaku dari skala kecil sampai astronomi. Di sisi lain, beberapa teknik tergantung pada laju terbatas cahaya, misalnya dalam pengukuran jarak.
Skala kecil
Dalam superkomputer, kecepatan cahaya memberlakukan batas pada seberapa cepat data dapat dikirim antara prosesor. Jika prosesor beroperasi pada 1 gigahertz, sinyal hanya dapat melakukan perjalanan maksimum sekitar 30 cm dalam satu siklus.
Prosesor karena itu harus ditempatkan dekat satu sama lain untuk meminimalkan latensi komunikasi; ini dapat menyebabkan kesulitan dengan pendingin. Jika frekuensi jam terus meningkat, laju cahaya pada akhirnya akan menjadi faktor pembatas untuk desain internal cip (sirkuit terpadu) tunggal.
Jarak yang besar di Bumi
Misalnya, diberikan lingkar ekuator Bumi adalah sekitar 40075 km dan c sekitar 300000 km/s, waktu tersingkat teoretis untuk sepotong informasi untuk melakukan perjalanan setengah dunia sepanjang permukaan adalah sekitar 67 milidetik.
Ketika cahaya berjalan di seluruh dunia dalam serat optik, waktu transit yang sebenarnya lebih panjang, sebagian karena kecepatan cahaya lebih lambat sekitar 35% dalam serat optik, tergantung pada indeks bias n-nya.
Selanjutnya, garis lurus jarang terjadi dalam situasi komunikasi global, dan penundaan terjadi ketika sinyal melewati sebuah switch elektronik atau regenerator sinyal.
Penerbangan ruang angkasa dan astronomi
Seberkas cahaya digambarkan bepergian antara Bumi dan Bulan dalam waktu yang dibutuhkan sebuah pulsa cahaya untuk bergerak di antara mereka: 1,255 detik pada rata-rata jarak orbital mereka (permukaan-ke-permukaan). Ukuran relatif dan pemisahan sistem Bumi-Bulan ditunjukkan sesuai skala.
Demikian pula, komunikasi antara Bumi dan pesawat ruang angkasa tidak seketika. Ada penundaan singkat dari sumber ke penerima, yang menjadi lebih terlihat ketika jarak meningkat. Penundaan ini adalah signifikan untuk komunikasi antara kontrol tanah dan Apollo 8 ketika menjadi pesawat ruang angkasa berawak pertama yang mengorbit Bulan: untuk setiap pertanyaan, stasiun kontrol tanah harus menunggu setidaknya tiga detik untuk jawaban tiba.
Penundaan komunikasi antara Bumi dan Mars bisa bervariasi antara lima dan dua puluh menit tergantung pada posisi relatif dari dua planet.
Sebagai konsekuensi dari ini, jika robot di permukaan Mars menghadapi masalah, pengendali manusia tidak akan menyadari hal itu sampai setidaknya 5 menit kemudian, dan mungkin sampai 20 menit kemudian; kemudian akan membutuhkan 5 – 20 menit untuk petunjuk untuk melakukan perjalanan dari Bumi ke Mars.
NASA harus menunggu beberapa jam untuk informasi dari pesawat ruang angkasa yang mengorbit Yupiter, dan jika perlu untuk memperbaiki kesalahan navigasi, perbaikan tidak akan sampai pada pesawat ruang angkasa untuk jumlah waktu yang sama, menciptakan risiko koreksi tidak tiba pada waktunya.
Menerima cahaya dan sinyal dari sumber astronomi jauh bahkan dapat memakan waktu lebih lama. Sebagai contoh, dibutuhkan 13 miliar (13×109) tahun untuk cahaya untuk melakukan perjalanan ke Bumi dari galaksi jauh dilihat dalam gambar Hubble Ultra Deep Field.
Foto-foto itu, yang diambil hari ini, menangkap gambar galaksi seperti mereka tampak 13 miliar tahun yang lalu, ketika alam semesta berusia kurang dari satu miliar tahun.
Fakta bahwa objek yang lebih jauh tampak lebih muda, karena laju cahaya yang terbatas, memungkinkan para astronom untuk menyimpulkan evolusi bintang, galaksi, dan alam semesta itu sendiri.
Jarak astronomi kadang-kadang dinyatakan dalam tahun cahaya, terutama dalam publikasi sains populer dan media.
Satu tahun cahaya adalah jarak yang ditempuh cahaya dalam satu tahun, sekitar 9461 miliar kilometer, 5879 miliar mil, atau 0,3066 parsec.
Dalam angka bulat, satu tahun cahaya adalah hampir 10 triliun kilometer atau hampir 6 triliun mil. Proxima Centauri, bintang terdekat dengan Bumi setelah Matahari, sekitar 4,2 tahun cahaya.
Pengukuran jarak
Sistem radar mengukur jarak ke target dengan waktu yang dibutuhkan pulsa gelombang radio untuk kembali ke antena radar setelah dipantulkan oleh target: jarak ke target adalah setengah waktu transit pulang-pergi yang dikalikan dengan laju cahaya.
Sebuah penerima Global Positioning System (GPS) mengukur jarak ke satelit GPS berdasarkan berapa lama waktu yang dibutuhkan untuk sinyal radio tiba dari setiap satelit, dan dari jarak ini menghitung posisi penerima.
Karena cahaya bergerak sekitar 300000 kilometer (186000 mi) dalam satu detik, pengukuran pecahan kecil dari detik harus sangat tepat. Lunar Laser Ranging Experiment, astronomi radar dan Deep Space Network menentukan jarak ke Bulan, planet dan pesawat ruang angkasa, secara berurutan, dengan mengukur waktu transit pulang-pergi.
Perdagangan frekuensi tinggi
Laju cahaya telah menjadi penting dalam perdagangan frekuensi tinggi, di mana para pedagang berusaha untuk mendapatkan keuntungan menit dengan memberikan perdagangan mereka untuk pertukaran pecahan detik lebih dulu dari pedagang lainnya.
Misalnya, pedagang telah beralih ke komunikasi gelombang mikro antara hub perdagangan, karena keuntungan gelombang mikro bepergian di dekat laju cahaya di udara, lebih dari sinyal serat optik yang bepergian 30-40% lebih lambat dari laju cahaya melalui kaca.
Pengukuran
Ada berbagai cara untuk menentukan nilai c. Salah satu cara adalah dengan mengukur laju yang sebenarnya di mana gelombang cahaya merambat, yang dapat dilakukan dengan berbagai setup astronomi dan berbasis-bumi.
Namun, hal ini juga memungkinkan untuk menentukan c dari hukum fisika lainnya di mana ia muncul, misalnya, dengan menentukan nilai-nilai konstanta elektromagnetik ε0 dan μ0 dan menggunakan hubungan mereka dengan c.
Secara historis, hasil yang paling akurat telah diperoleh dengan secara terpisah menentukan frekuensi dan panjang gelombang sinar, dengan produk mereka menyamai c.
Pada tahun 1983 meter didefinisikan sebagai:
“Panjang jalan yang ditempuh oleh cahaya dalam ruang hampa selama selang waktu dari 1⁄299792458 detik”.
Menetapkan nilai laju cahaya di 299792458 m/s dengan definisi, seperti yang dijelaskan di bawah ini. Akibatnya, pengukuran akurat dari kecepatan cahaya menghasilkan realisasi akurat dari meter daripada nilai yang akurat dari c.
Pengukuran astronomis
Luar angkasa adalah pengaturan nyaman untuk mengukur laju cahaya karena skala besar dan vakum hampir sempurna. Biasanya, seseorang mengukur waktu yang dibutuhkan untuk cahaya untuk melintasi jarak referensi dalam tata surya, seperti jari-jari orbit bumi.
Secara historis, pengukuran tersebut dapat dibuat cukup akurat, dibandingkan dengan seberapa akurat panjang jarak referensi dikenal di unit berbasis Bumi. Sudah menjadi adat untuk mengekspresikan hasil dalam satuan astronomi (SA) per hari.
Ole Christensen Rømer menggunakan pengukuran astronomis untuk membuat estimasi kuantitatif pertama dari laju cahaya. Ketika diukur dari Bumi, periode bulan yang mengorbit sebuah planet lebih pendek saat Bumi mendekati planet daripada ketika bumi sedang menjauhinya.
Jarak yang ditempuh oleh cahaya dari planet (atau bulannya) ke Bumi lebih pendek saat Bumi berada pada titik di orbitnya yang paling dekat dengan planet dibandingkan saat Bumi berada pada titik terjauh di orbitnya, perbedaan jarak adalah diameter orbit Bumi mengelilingi Matahari.
Perubahan yang diamati dalam periode orbit bulan disebabkan oleh perbedaan waktu yang dibutuhkan cahaya untuk melintasi jarak yang lebih pendek atau lebih panjang. Rømer mengamati efek ini untuk bulan terdalam Yupiter Io dan menyimpulkan bahwa cahaya memerlukan 22 menit untuk menyeberangi diameter orbit bumi.
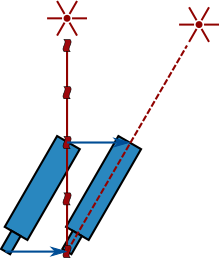
Cara lain adalah dengan menggunakan aberasi cahaya, ditemukan dan dijelaskan oleh James Bradley pada abad ke-18. Efek ini hasil dari penjumlahan vektor dari laju cahaya yang datang dari sumber yang jauh (seperti bintang) dan kecepatan pengamat (lihat diagram di sebelah kanan), sehingga seorang pengamat yang bergerak melihat cahaya yang datang dari arah yang sedikit berbeda dan akibatnya melihat sumber di posisi yang bergeser dari posisi semula.
Karena arah kecepatan bumi berubah terus-menerus ketika Bumi mengorbit Matahari, efek ini menyebabkan posisi tampak bintang untuk bergerak.
Dari perbedaan sudut dalam posisi bintang (maksimal 20,5 detik busur) adalah mungkin untuk mengekspresikan laju cahaya dalam hal kecepatan Bumi mengelilingi matahari, yang dengan panjang diketahui dari setahun dapat dikonversi ke waktu yang dibutuhkan untuk perjalanan dari Matahari ke Bumi.
Pada 1729, Bradley menggunakan metode ini untuk mendapatkan bahwa cahaya melakukan perjalanan 10.210 kali lebih cepat dari Bumi di orbitnya (angka modern 10.066 kali lebih cepat) atau, secara setara, bahwa cahaya membutuhkan 8 menit 12 detik untuk melakukan perjalanan dari Matahari ke Bumi.
Satuan astronomi
Satuan astronomi (SA) adalah kira-kira jarak rata-rata antara Bumi dan Matahari. SA didefinisikan kembali pada tahun 2012 sebagai persis 149597870700 m.
Sebelumnya SA tidak didasarkan pada Sistem Satuan Internasional tetapi dalam hal gaya gravitasi yang diberikan oleh Matahari dalam mekanika klasik.
Definisi saat ini menggunakan nilai yang direkomendasikan dalam meter untuk definisi satuan astronomi sebelumnya, yang ditentukan oleh pengukuran. Redefinisi ini analog dengan meter, dan juga memiliki efek menetapkan laju cahaya ke nilai yang tepat dalam satuan astronomi per detik (melalui laju cahaya yang tepat dalam meter per detik).
Sebelumnya, kebalikan dari c dinyatakan dalam detik per satuan astronomi diukur dengan membandingkan waktu untuk sinyal radio untuk mencapai pesawat ruang angkasa yang berbeda di Tata Surya, dengan posisi mereka dihitung dari efek gravitasi Matahari dan berbagai planet.
Dengan menggabungkan banyak pengukuran tersebut, nilai terbaik untuk waktu cahaya per satuan jarak dapat diperoleh. Misalnya, pada tahun 2009, estimasi terbaik, yang disetujui oleh International Astronomical Union (IAU), adalah:
Waktu cahaya untuk satuan jarak: 499.004783836(10) s
c = 0.00200398880410(4) SA/s = 173.144632674(3) SA/hari.
Ketidakpastian relatif dalam pengukuran ini adalah 0,02 bagian per miliar (2×10−11), setara dengan ketidakpastian dalam pengukuran panjang berbasis Bumi dengan interferometri.
Sejak meter didefinisikan sebagai jarak tempuh cahaya dalam interval waktu tertentu, pengukuran waktu cahaya dalam hal definisi sebelumnya satuan astronomi juga dapat diartikan sebagai mengukur panjang satu SA (definisi lama) dalam meter.
Teknik waktu terbang
Sebuah metode pengukuran laju cahaya adalah untuk mengukur waktu yang dibutuhkan untuk cahaya untuk melakukan perjalanan ke cermin di jarak yang diketahui dan kembali. Ini adalah prinsip yang bekerja pada aparatus Fizeau-Foucault yang dikembangkan oleh Hippolyte Fizeau dan Léon Foucault.
Setup seperti yang digunakan oleh Fizeau terdiri dari seberkas cahaya diarahkan pada cermin 8 kilometer (5 mi) jauhnya. Dalam perjalanan dari sumber ke cermin, berkas cahaya melewati roda bergigi yang berputar.
Pada tingkat tertentu rotasi, berkas cahaya melewati satu celah di jalan keluar dan celah lain dalam perjalanan kembali, tetapi pada tingkat sedikit lebih tinggi atau lebih rendah, berkas cahaya menghantam gigi dan tidak melewati roda.
Mengetahui jarak antara roda dan cermin, jumlah gigi pada roda, dan tingkat rotasi, laju cahaya dapat dihitung.
Metode Foucault menggantikan roda bergigi dengan cermin berputar. Karena cermin terus berputar sementara cahaya berjalan ke cermin jauh dan kembali, cahaya dipantulkan dari cermin berputar pada sudut yang berbeda pada jalan keluar daripada di jalan kembali. Dari perbedaan sudut ini, kelajuan rotasi dan jarak ke cermin jauh yang diketahui laju cahaya dapat dihitung.
Saat ini, menggunakan osiloskop dengan resolusi waktu kurang dari satu nanodetik, laju cahaya dapat langsung diukur dengan waktu penundaan pulsa cahaya dari laser atau LED dipantulkan dari cermin. Metode ini kurang tepat (dengan kesalahan dari urutan 1%) daripada teknik modern lainnya, tetapi kadang-kadang digunakan sebagai percobaan laboratorium di kelas fisika perguruan tinggi.
Konstanta elektromagnetik
Opsi untuk menurunkan c yang tidak secara langsung tergantung pada pengukuran perambatan gelombang elektromagnetik adalah dengan menggunakan hubungan antara c dan permitivitas vakum ε0 dan permeabilitas vakum μ0 didirikan oleh teori Maxwell: c2 = 1/(ε0μ0).
Permitivitas vakum dapat ditentukan dengan mengukur kapasitansi dan dimensi kapasitor, sedangkan nilai permeabilitas vakum adalah tetap di persis 4π×10−7 H⋅m−1 melalui definisi ampere. Rosa dan Dorsey menggunakan metode ini pada tahun 1907 untuk menemukan nilai 299710±22 km/s.
Resonansi cavity
Cara lain untuk mengukur laju cahaya adalah dengan secara terpisah mengukur frekuensi f dan panjang gelombang λ dari gelombang elektromagnetik dalam vakum. Nilai ckemudian didapatkan dengan hubungan c = fλ. Satu pilihan adalah mengukur frekuensi resonansi dari sebuah cavity resonator.
Jika dimensi cavity resonansi juga diketahui, ini dapat digunakan untuk menentukan panjang gelombang dari gelombang itu.
Pada tahun 1946, Louis Essen dan A.C. Gordon-Smith menentukan frekuensi dari sebuah macam dari mode normal dari gelombang mikro dari microwave cavity dengan dimensi yang diketahui dengan teliti.
Dimensi ditentukan ke akurasi sekitar ±0,8 μm dengan gauge yang dikalibrasi dengan interferometri.
Karena panjang gelombang mode diketahui dari geometri cavity dan dari teori elektromagnetik, pengetahuan dari frekuensi yang terkait memungkinkan penghitungan panjang gelombang.
Hasil Essen-Gordon-Smith, 299792±9 km/s, secara substansial lebih tepat daripada yang ditemukan dengan teknik optik. Pada tahun 1950, pengukuran ulang oleh Essen menetapkan hasil 299792.5±3.0 km/s.
Sebuah demonstrasi rumah tangga dari teknik ini adalah mungkin, menggunakan oven gelombang mikro dan makanan seperti marshmallow atau margarin. Jika meja putar diambil sehingga makanan tidak bergerak, itu akan memasak tercepat di antinode (titik-titik di mana amplitudo gelombang adalah yang terbesar), di mana ia akan mulai mencair.
Jarak antara dua titik tersebut adalah setengah panjang gelombang dari gelombang mikro; dengan mengukur jarak ini dan mengalikan panjang gelombang dengan frekuensi gelombang mikro (biasanya ditampilkan di bagian belakang oven, biasanya 2450 MHz), nilai c dapat dihitung, “sering dengan kurang dari kesalahan 5%”.
Interferometri
Interferometri adalah metode lain untuk menemukan panjang gelombang radiasi elektromagnetik untuk menentukan laju cahaya. Seberkas cahaya koheren(misalnya dari laser), dengan frekuensi dikenal (f), dibagi untuk mengikuti dua jalur dan kemudian digabungkan.
Dengan menyesuaikan panjang jalur sambil mengamati pola interferensi dan dengan hati-hati mengukur perubahan panjang jalur, panjang gelombang cahaya (λ) dapat ditentukan. Laju cahaya kemudian dihitung menggunakan persamaan c = λf.
Sebelum munculnya teknologi laser, sumber radio yang koheren digunakan untuk pengukuran interferometri dari laju cahaya. Namun penentuan interferometri dari panjang gelombang semakin kurang tepat seiring bertambahnya panjang gelombang sehingga percobaan terbatas dalam presisi oleh gelombang panjang (~0,4 cm) dari gelombang radio.
Presisi dapat ditingkatkan menggunakan cahaya dengan panjang gelombang yang lebih pendek, tetapi kemudian menjadi sulit untuk langsung mengukur frekuensi cahaya.
Salah satu cara mengatasi masalah ini adalah mulai dengan sinyal frekuensi rendah dari frekuensi yang dapat diukur dengan tepat, dan dari sinyal ini semakin mensintesis sinyal frekuensi yang lebih tinggi yang frekuensinya dapat dihubungkan dengan sinyal asli.
Sebuah laser kemudian dapat dikunci untuk frekuensi, dan panjang gelombang dapat ditentukan dengan interferometri.
Teknik ini adalah karena kelompok di National Bureau of Standards (NBS) (yang kemudian menjadi NIST). Mereka menggunakannya pada tahun 1972 untuk mengukur laju cahaya dalam ruang hampa dengan ketidakpastian pecahan 3,5 × 10-9.3.5×10−9.
Sejarah pengukuran kecepatan cahaya
| <1638 | Galileo, lentera tertutup | inkonklusif |
| <1667 | Accademia del Cimento, lentera tertutup | inkonklusif |
| 1675 | Rømer dan Huygens, bulan Yupiter | 220000 |
| 1729 | James Bradley, aberasi cahaya | 301000 |
| 1849 | Hippolyte Fizeau, roda bergigi | 315000 |
| 1862 | Léon Foucault, cermin berotasi | 298000±500 |
| 1907 | Rosa and Dorsey, konstanta EM | 299710±30 |
| 1926 | Albert A. Michelson, cermin berotasi | 299796±4 |
| 1950 | Essen and Gordon-Smith, resonator cavity | 299792.5±3.0 |
| 1958 | K.D. Froome, interferometri radio | 299792.50±0.10 |
| 1972 | Evenson et al., interferometri laser | 299792.4562±0.0011 |
| 1983 | CGPM ke-17, definisi meter | 299792.458 (eksak) |
Sampai periode modern awal, tidak diketahui apakah perjalanan cahaya seketika atau pada laju sangat cepat yang terbatas. Penelitian masih ada yang tercatat pertama dari hal ini adalah di Yunani Kuno.
Orang Yunani Kuno, cendekiawan Muslim, dan ilmuwan Eropa klasik lama memperdebatkan ini sampai Rømer memberikan perhitungan pertama dari laju cahaya.
Teori Relativitas Khusus Einstein menyimpulkan bahwa laju cahaya adalah konstan terlepas dari bingkai seseorang acuan. Sejak itu, para ilmuwan telah memberikan pengukuran yang semakin akurat.
Sejarah awal kecepatan cahaya
Empedocles (c. 490-430 SM) adalah orang pertama yang mengusulkan teori cahaya dan mengklaim bahwa cahaya memiliki laju yang terbatas. Ia mempertahankan bahwa cahaya adalah sesuatu yang bergerak, dan karena itu memerlukan waktu untuk perjalanan.
Aristoteles berpendapat, sebaliknya, bahwa “cahaya adalah karena kehadiran sesuatu, tetapi bukan gerakan”. Euklides dan Ptolemaeus memajukan teori emisi penglihatan Empedocles, di mana cahaya dipancarkan dari mata, sehingga memungkinkan melihat.
Berdasarkan teori itu, Heron dari Alexandria berpendapat bahwa laju cahaya harus tak hinggakarena objek yang jauh seperti bintang muncul segera setelah membuka mata. Filsuf awal Islam awalnya setuju dengan pandangan Aristoteles bahwa cahaya tidak memiliki laju perjalanan.
Pada tahun 1021, Alhazen (Ibnu Haitham) menerbitkan Kitab Optik, di mana ia menyajikan serangkaian argumen yang menolak teori emisi penglihatan yang mendukung teori intromisi yang sekarang diterima, di mana cahaya bergerak dari objek ke mata.
Hal ini menyebabkan Alhazen untuk mengusulkan bahwa cahaya harus memiliki laju yang terbatas dan bahwa laju cahaya adalah variabel, menurun dalam benda yang lebih padat.
Ia berpendapat bahwa cahaya adalah materi substansial, perambatannya membutuhkan waktu, bahkan jika ini tersembunyi dari indra kita.
Juga pada abad ke-11, al-Biruni sepakat bahwa cahaya memiliki kecepatan yang terbatas, dan mengamati bahwa laju cahaya jauh lebih cepat dari kelajuan suara.
Pada abad ke-13, Roger Bacon berpendapat bahwa laju cahaya di udara terbatas, menggunakan argumen filosofis yang didukung oleh penulisan Alhazen dan Aristoteles.
Pada tahun 1270-an, Witelo mempertimbangkan kemungkinan cahaya bergerak dengan laju tak hingga dalam ruang hampa, tetapi melambat dalam benda yang lebih padat. Pada abad ke-14, Sayana telah membuat pernyataan tentang laju cahaya dalam komentarnya pada Hindu Regweda.
Pada awal abad ke-17, Johannes Kepler percaya bahwa laju cahaya adalah terbatas, karena ruang kosong tidak memberikan halangan pada cahaya.
René Descartes berpendapat bahwa jika laju cahaya terbatas, Matahari, Bumi, dan Bulan akan keluar dari kesejajaran saat gerhana bulan. Karena salah penjajaran tersebut belum diamati, Descartes menyimpulkan laju cahaya adalah terbatas. Descartes berspekulasi bahwa jika laju cahaya terbatas, seluruh sistem filsafatnya mungkin hancur.
Dalam derivasi Descartes dari hukum Snell, dia berasumsi bahwa meskipun laju cahaya adalah sesaat, semakin padat medium, semakin cepat laju cahaya.
Pierre de Fermat menurunkan hukum Snell menggunakan asumsi yang berlawanan, semakin padat medium semakin lambat cahaya bergerak. Fermat juga berpendapat dalam mendukung kecepatan terbatas cahaya.
Usaha pengukuran kecepatan cahaya pertama
Pada tahun 1629, Isaac Beeckman mengusulkan sebuah percobaan di mana seseorang mengamati kilatan meriam terpantul dari cermin sekitar satu mil (1,6 km) jauhnya.
Pada tahun 1638, Galileo Galilei mengusulkan eksperimen, dengan klaim yang jelas telah melakukan itu beberapa tahun sebelumnya, untuk mengukur laju cahaya dengan mengamati penundaan antara membuka lentera dan persepsi di tempat yang agak jauh. Ia tidak dapat membedakan apakah perjalanan cahaya seketika atau tidak, tetapi menyimpulkan bahwa jika tidak, itu harus tetap menjadi luar biasa cepat.
Pada 1667, Accademia del Cimento dari Florence melaporkan bahwa mereka telah melakukan percobaan Galileo, dengan lentera berjarak sekitar satu mil, tetapi tidak ada penundaan yang diamati. Penundaan yang sebenarnya dalam percobaan ini akan menjadi sekitar 11 mikrodetik.
Perkiraan kuantitatif pertama dari laju cahaya dibuat pada 1676 oleh Rømer (lihat Determinasi Rømer dari laju cahaya). Dari pengamatan bahwa periode bulan terdalam Yupiter Io tampak lebih pendek ketika Bumi mendekati Yupiter daripada ketika menjauhi dari itu, ia menyimpulkan bahwa cahaya berjalan pada laju yang terbatas, dan memperkirakan bahwa cahaya membutuhkan 22 menit untuk menyeberangi diameter orbit bumi.
Christiaan Huygens mengkombinasikan perkiraan ini dengan perkiraan untuk diameter orbit bumi untuk mendapatkan perkiraan laju cahaya 220000 km/s, 26% lebih rendah dari nilai yang sebenarnya.
Pada bukunya tahun 1704 Opticks, Isaac Newton melaporkan perhitungan Rømer untuk laju terbatas cahaya dan memberikan nilai “tujuh atau delapan menit” untuk waktu yang dibutuhkan untuk cahaya untuk perjalanan dari matahari ke bumi (nilai modern 8 menit 19 detik).
Newton bertanya apakah bayangan gerhana Rømer ini berwarna; mendengar bahwa mereka tidak, ia menyimpulkan warna yang berbeda bergerak pada laju yang sama. Pada 1729, James Bradley menemukan aberasi bintang.
Dari efek ini ia menentukan bahwa cahaya harus bergerak 10.210 kali lebih cepat dari Bumi di orbitnya (angka modern 10.066 kali lebih cepat) atau, sama, bahwa cahaya akan memerlukan 8 menit 12 detik untuk perjalanan dari matahari ke bumi.
Hubungan dengan elektromagnetisme
Pada abad ke-19 Hippolyte Fizeau mengembangkan metode untuk menentukan laju cahaya berdasarkan pengukuran waktu terbang di Bumi dan melaporkan nilai 315000 km/s. Metodenya diperbaiki oleh Léon Foucault yang memperoleh nilai 298000 km/s pada tahun 1862.
Pada tahun 1856, Wilhelm Eduard Weber dan Rudolf Kohlrausch mengukur rasio unit elektromagnetik dan elektrostatik dari muatan, 1/√ε0μ0, dengan melepaskan muatan dari tabung Leyden, dan menemukan bahwa nilai numeriknya sangat dekat dengan laju cahaya yang diukur langsung oleh Fizeau.
Tahun berikutnya Gustav Kirchhoff menghitung bahwa sinyal listrik dalam kawat tanpa hambatan berjalan sepanjang kawat pada kelajuan ini.
Pada tahun 1860-an awal, Maxwell menunjukkan bahwa, menurut teori elektromagnetisme yang dia kerjakan, gelombang elektromagnetik merambat di ruang kosong pada kelajuan yang sama dengan rasio Weber/Kohrausch di atas, dan menarik perhatian terhadap kedekatan numerik dari nilai ini dengan laju cahaya yang diukur oleh Fizeau, ia mengusulkan bahwa cahaya sebenarnya merupakan gelombang elektromagnetik.
“Luminiferous aether”
Dipikirkan pada saat itu bahwa ruang kosong diisi dengan media latar belakang yang disebut luminiferous aether di mana medan elektromagnetik ada. Beberapa fisikawan berpikir bahwa aether ini bertindak sebagai kerangka terpilih acuan untuk perambatan cahaya dan karena itu harus mungkin untuk mengukur gerakan bumi sehubungan dengan media ini, dengan mengukur isotropi kecepatan cahaya.
Dimulai pada tahun 1880-an beberapa percobaan dilakukan untuk mencoba mendeteksi gerakan ini, yang paling terkenal adalah percobaan yang dilakukan oleh Albert A. Michelson dan Edward W. Morley pada tahun 1887.
Gerakan yang terdeteksi selalu kurang dari kesalahan pengamatan. Percobaan modern menunjukkan bahwa laju dua arah cahaya adalah isotropik (sama di setiap arah) hingga 6 nanometer per detik.
Karena percobaan ini Hendrik Lorentz mengusulkan bahwa gerak aparatus melalui aether dapat menyebabkan aparatur untuk berkontraksi sepanjang panjangnya dalam arah gerakan. Ia lebih lanjut berasumsi, bahwa variabel waktu untuk sistem bergerak juga harus diubah sesuai (“waktu setempat”), yang menyebabkan perumusan transformasi Lorentz.
Berdasarkan teori aether Lorentz ini, Henri Poincaré (1900) menunjukkan bahwa waktu setempat ini (ke urutan pertama dalam v/c) ditunjukkan dengan jam bergerak dalam aether, yang disinkronkan dengan asumsi kecepatan cahaya konstan.
Pada tahun 1904, ia berspekulasi bahwa laju cahaya bisa menjadi kecepatan pembatas dalam dinamika, asalkan semua asumsi teori Lorentz ini dikonfirmasi. Pada tahun 1905, Poincaré membawa teori aether Lorentz ke dalam perjanjian observasional penuh dengan prinsip relativitas.
Relativitas khusus Einstein
Pada tahun 1905 Einstein mendalilkan dari awal bahwa laju cahaya dalam ruang hampa, diukur oleh pengamat yang tidak dipercepat, independen dari gerakan sumber atau pengamat.
Menggunakan ini dan prinsip relativitas sebagai dasar ia menurunkan teori relativitas khusus, di mana laju cahaya dalam ruang hampa c menjadi sebuah konstanta dasar, juga muncul dalam konteks yang tidak terkait dengan cahaya.
Hal ini membuat konsep aether stasioner (yang masih dianut Lorentz dan Poincare) tidak berguna dan merevolusi konsep ruang dan waktu.
Peningkatan akurasi c dan redefinisi meter dan detik
Pada paruh kedua abad ke-20 banyak kemajuan dibuat dalam meningkatkan akurasi pengukuran laju cahaya, pertama dengan teknik resonansi cavity dan kemudian dengan teknik interferometer laser. Ini dibantu oleh definisi meter dan detik yang baru dan lebih tepat. Pada tahun 1950, Louis Essen menentukan laju cahaya sebagai 299792.5±1 km/s, menggunakan resonansi cavity.
Nilai ini diadopsi oleh Majelis Umum ke-12 dari Radio-Scientific Union pada tahun 1957. Pada tahun 1960, meter didefinisikan kembali berdasarkan panjang gelombang garis spektrum tertentu kripton-86, dan, pada tahun 1967, detik didefinisikan kembali berdasarkan frekuensi transisi hyperfine dari keadaan dasar sesium-133.
Pada tahun 1972, menggunakan metode laser interferometer dan definisi baru, sebuah kelompok di NBS di Boulder, Colorado menentukan laju cahaya dalam ruang hampa menjadi c = 299792456.2±1.1 m/s. Ini adalah 100 kali lebih pasti dari nilai yang diterima sebelumnya. Ketidakpastian yang tersisa terutama terkait dengan definisi meter.
Karena percobaan serupa menemukan hasil yang sebanding untuk c, Konferensi Umum mengenai Berat dan Ukuran (bahasa Perancis: Conférence générale des poids et mesures, CGPM) ke-15 pada tahun 1975 merekomendasikan menggunakan nilai 299792458 m/s untuk laju cahaya.
Mendefinisikan laju cahaya sebagai konstanta eksplisit
Pada tahun 1983 CGPM ke-17 menemukan bahwa panjang gelombang dari pengukuran frekuensi dan nilai yang diberikan untuk laju cahaya lebih dapat direproduksi dari standar sebelumnya. Mereka mempertahankan definisi detik tahun 1967, sehingga frekuensi hyperfine sesium sekarang akan menentukan baik detik dan meter.
Untuk melakukan hal ini, mereka mendefinisikan ulang meter sebagai: “Meter adalah panjang jarak yang ditempuh oleh cahaya dalam ruang hampa selama selang waktu dari 1/299792458 detik.” Sebagai hasil dari definisi ini, nilai laju cahaya dalam ruang hampa adalah secara eksak 299792458 m/s dan telah menjadi konstanta yang didefinisikan dalam sistem satuan SI.
Peningkatan teknik eksperimental yang sebelum 1983 akan mengukur laju cahaya, tidak lagi memengaruhi nilai yang diketahui dari laju cahaya dalam satuan SI, melainkan memungkinkan realisasi yang lebih tepat dari meter dengan secara lebih akurat mengukur panjang gelombang Kripton-86 dan sumber cahaya lainnya.
Pada tahun 2011, CGPM menyatakan niatnya untuk mendefinisikan ketujuh satuan dasar SI menggunakan apa yang disebut “formulasi konstanta eksplisit”, di mana setiap “satuan didefinisikan secara tidak langsung dengan menentukan secara eksplisit nilai yang pasti untuk sebuah konstanta dasar yang diakui”, seperti yang dilakukan untuk laju cahaya.
CGPM mengusulkan kata-kata dari definisi meter yang baru, tetapi benar-benar setara:
“Meter, simbol m, adalah satuan panjang besarnya diatur dengan menetapkan nilai numerik dari laju cahaya dalam ruang hampa untuk menjadi sama dengan secara eksak 299792458 bila dinyatakan dalam satuan SI m s−1.” Ini adalah salah satu perubahan yang diusulkan untuk dimasukkan dalam revisi berikutnya dari SI yang juga disebut SI Baru.
Bacaan Lainnya
- Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Induksi Elektromagnetik – Hukum Faraday dan Hukum Lenz – Soal dan Jawaban
- Konstanta Dielektrik – Permitivitas Listrik
- Hukum Gauss (medan listrik) | Integral, Fungsi, Rumus, Soal dan Jawaban
- Elektrodinamika | Penjelasan, Rumus, Contoh Soal dan Jawaban
- Hukum Faraday 1 dan 2 | Hukum Induksi Faraday, Rumus, Soal dan Jawaban
- Rumus Energi Potensial Fisika | Rumus, Penjelasan, Contoh Soal dan Jawaban
- Induksi dan Fluks Magnetik Bersama Contoh Soal dan Jawaban
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Space, Cosmos Magazine, Britannica, University of Virginia, Swinburne University of Technology, Science Alert
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing