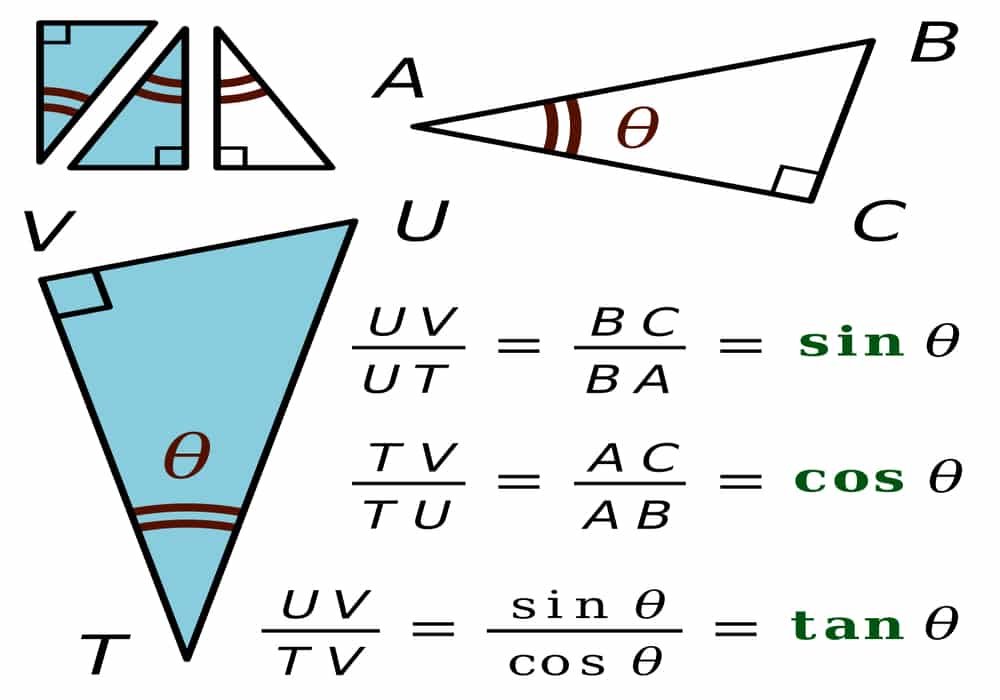
Trigonometri Sinus, Cosinus, Tangen, Secan, Cosecan, Cotangen

Berikut adalah rumus-rumus: Sinus, Cosinus, Tangen, Secan, Cosecan, Cotangen.

Sinus

Dalam trigonometri, hukum sinus ialah sebuah persamaan yang berhubungan dengan panjang sisi-sisi sebuah segitiga yang berubah-ubah terhadap sinus sudutnya.

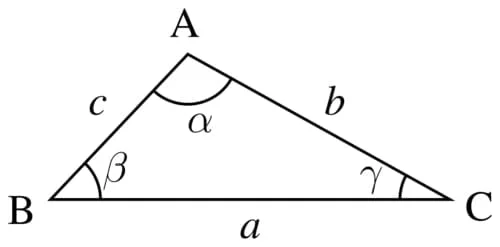
Jika sisi segitiga ialah (kasus sederhana) a, b dan c dan sudut yang berhadapan bersisi (huruf besar) A, B and C, hukum sinus menyatakan:

sinA = sinB = sinC
____ ____ ____
a b c

Multiple-angle formulae

Rumus ini berguna menghitung sisi yang tersisa dari segitiga jika 2 sudut dan 1 sisinya diketahui, masalah umum dalam teknik triangulasi. Dapat juga digunakan saat 2 sisi dan 1 dari sudut yang tak dilampirkan diketahui; dalam kasus ini, rumus ini dapat memberikan 2 nilai penting untuk sudut yang dilampirkan. Saat ini terjadi, sering hanya 1 hasil akan menyebabkan seluruh sudut kurang daripada 180°; dalam kasus lain, ada 2 penyelesaian valid pada segitiga.

Timbal balik bilangan yang yang digambarkan dengan hukum sinus (yakni a/sin(A)) sama dengan diameter d . Kemudian hukum ini dapat dituliskan

a b c
____ = ____ = ____ = d
Sin A sin B sin C

Dapat ditunjukkan bahwa:

abc 2abc
d = ___________________ = ___________________________
2√ s(s-a) (s-b) (s-c) √ (a²+b²+c²)² + 2 (a⁴+b⁴+c⁴)

yang di mana

s merupakan semi-perimeter

(a+b+c)
s = ________
2

Turunan Sinus

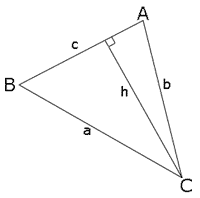
Buatlah segitiga dengan sisi a, b, dan c, dan sudut yang berlawanan A, B, dan C. Buatlah garis dari sudut C pada sisi lawannya c yang menonjol sekali dalam 2 segitiga siku-siku, dan sebut panjang garis ini h.

Dapat diamati bahwa:

h h
sin A = ___ dan sin B = __
b a

Kemudian:

h = b sin A = α sin B

dan

sin A sin B
_____ = _____
a b

Melakukan hal yang sama dengan garis yang digambarkan antara sudut A dan sisi a akan menghasilkan:
sin B = sin C
_____ _____
b c

Cosinus

Hukum kosinus, atau disebut juga aturan kosinus, dalam trigonometri adalah aturan yang memberikan hubungan yang berlaku dalam suatu segitiga, yaitu antara panjang sisi-sisi segitiga dan kosinus dari salah satu sudut dalam segitiga tersebut.

Perhatikan gambar segitiga ini.

Aturan kosinus menyatakan bahwa

c² = a² + b² – 2ab cos γ

dengan $\gamma \,$ adalah sudut yang dibentuk oleh sisi a dan sisi b, dan c adalah sisi yang berhadapan dengan sudut $\gamma \,$ .

Aturan yang sama berlaku pula untuk sisi a dan b:

a² = b² + c² – 2bc cos α
b² = a² + c² – 2ac cos β

Dengan kata lain, bila panjang dua sisi sebuah segitiga dan sudut yang diapit oleh kedua sisi tersebut diketahui, maka kita dapat menentukan panjang sisi yang satunya.

Sebaliknya, jika panjang dari tiga sisi diketahui, kita dapat menentukan besar sudut dalam segitiga tersebut. Dengan mengubah sedikit aturan kosinus tadi, kita peroleh:

b² + c² -a²
cos α = _____________
2bc

a² + c² – b²
cos β = ___________
2ac

a² + b² – c²
cos γ = ___________
2ab

Hukum Kosinus Pertama

a = b cos γ + c cos β
b = c cos α + a cos γ
c = a cos β + b cos α

Hukum Kosinus Kedua

a² = b² + c² – 2bc cos α
b² = a² + c² – 2ac cos β
c²= a² + b² – 2ab cos γ

Tangen

Tangen (lambang tg, tan; bahasa Belanda: tangens; bahasa Inggris: tangent) dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi segitiga yang terletak di sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o).

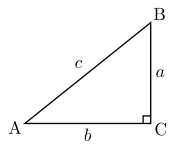
Berdasarkan segitiga pada ilustrator, berdasarkan definisi tangen, di atas maka nilai tangen adalah:

a b
tan A = ___ tan B = ___
b a

Nilai tangen positif di kuadran I dan III dan negatif di kuadran II dan IV.

Hubungan Nilai Tangen dengan Nilai Sinus dan Cosinus

SinA
tan A = ______
CosA

Nilai Tangen Sudut Istimewa

tan 0° = 0
tan 15° = 2 – √3
tan 300 = √3 / 3
tan 45° = 1
tan 60° = √3
tan 75° = 2 + √3
tan 90° = ∞

Secan (sekan)

Sekan (lambang: sec; bahasa Inggris: secant) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak pada sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga di kanan; berdasarkan definisi sekan di atas maka nilai sekan adalah:

c c
sec A = ____ sec B = ____
b a

Hubungan sekan dengan kosinus:

1
sec A = _____
cos A

Cosecan (kosekan)

Kosekan (disimbolkan dengan cosec atau csc; bahasa Inggris: cosecant) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga; berdasarkan definisi kosekan di atas maka nilai kosekan adalah:

c c
csc A = ____ csc B = ____
a b

Hubungan kosekan dengan sinus:

1
csc A = _____
sin A

Cotangen (kotangen)

Kotangen (lambang: cot, cotg, atau cotan; bahasa Inggris: cotangent) dalam matematika adalah perbandingan sisi segitiga yang terletak pada sudut dengan sisi segitiga yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o).

Perhatikan segitiga tersebut; berdasarkan definisi kotangen di atas maka nilai kotangen adalah:

b a
cot A = ___ cot B = ___
a b

Hubungan kotangen dengan tangen:

1
cot A = _____
tan A

Soal dan Jawaban Trigonometri

1. Tentukan luas segitiga:

Luas segitiga = ½ 3.5. sin 30^o = ½.3.5.½ = 15/4 = 3,75 cm

Untuk contoh soal dan jawaban trigonometri lainnya , mohon klik disini (akan membuka layar baru).

2. Pada ∆ ABC diketahui a+b=10 , sudut A=30˚ dan sudut 45˚ , maka panjang sisi b adalah…

Jawaban:
a+b=10
a=10-b
Aturan Sinus
a/sin A = b/sin B
10-b/ sin 30 = b/sin 45
10-b/1/2= b/√2/2
√2/2(10-b)=b/2
(10√2-b√2)/2=b/2
5√2-b√2/2=b/2
5√2=b√2/2 + b/2
5√2=(b√2+b)/2
5√2=b(√2+1)/2
b=5√2 x 2/(√2+1)
b=10√2/(√2+1) x (√2-1)/(√2-1)
b=20-10√2
b=10(2-√2)

3. Buktikan bahwa sin⁴ α – sin² α = cos⁴ α – cos² α

Jawaban:

sin⁴ α – sin² α = (sin²α)² – sin² α= (1 cos² α)²– (1 cos² α)= 1 – 2 cos² α + cos⁴ α – 1 + cos² α= cos⁴ α – cos² α

4. Pada segitiga ABC lancip, diketahui cos A = 4/5 dan sin B =12/ 13 , maka sin C =

Jawaban:
Karena segitiga ABC lancip , maka sudut A,B dan C juga lancip, sehingga :
cos A = 4/5, maka sin A = 3/5, (ingat cosami, sindemi dan tandesa)
sin B = 12/13, maka cos B = 5/13
A + B + C = 180°, (jml sudut -sudut dalam satu segitiga = 180)
A + B = 180 – C
sin (A + B) = sin (180 – C)
sin A . cos B + cos A.sin B = sin C, (ingat sudut yang saling berelasi : sin(180-x) = sin x)
sin C = sin A.cos B + cos A.sin B
sin C = 3/5.5/13 + 4/5.12/13
sin C = 15/65 + 48/65 = 63/65

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Sciencing, Clark University, SOS Math

Trigonometri Rumus: Sinus, Cosinus, Tangen, Secan, Cosecan, Cotangen

Trigonometri Sinus, Cosinus, Tangen, Secan, Cosecan, Cotangen

Sinus

Jika sisi segitiga ialah (kasus sederhana) a, b dan c dan sudut yang berhadapan bersisi (huruf besar) A, B and C, hukum sinus menyatakan: