PINTERpandai
Pinter Pandai

Rumus Integral dan Tabel Integral Kalkulus Beserta Contoh Soal dan Jawaban

4 min read

Integral Kalkulus

Integral Kalkulus

Integral adalah sebuah konsep penjumlahan secara berkesinambungan dalam matematika, dan bersama dengan inversnya, diferensiasi, adalah satu dari dua operasi utama dalam kalkulus. Temukan dibawah ini rumus integral kalkulus.

Integral dikembangkan menyusul dikembangkannya masalah dalam diferensiasi di mana matematikawan harus berpikir bagaimana menyelesaikan masalah yang berkebalikan dengan solusi diferensiasi. Lambang integral adalah {\displaystyle \int \,}

Bila diberikan suatu fungsif dari variabel realx dengan interval [a, b] dari sebuah garis lurus, maka integral tertentu

{\displaystyle \int _{a}^{b}\!f(x)\,dx\,}

didefinisikan sebagai area yang dibatasi oleh kurva f, sumbu-x, sumbu-y dan garis vertikal x = a dan x = b, dengan area yang berada di atas sumbu-x bernilai positif dan area di bawah sumbu-x bernilai negatif.

Kata integral juga dapat digunakan untuk merujuk pada antiturunan, sebuah fungsi F yang turunannya adalah fungsi f. Pada kasus ini, maka disebut sebagai integral tak tentu dan notasinya ditulis sebagai:

{\displaystyle F=\int f(x)\,dx.}

Prinsip-prinsip dan teknik integrasi dikembangkan terpisah oleh Isaac Newton dan Gottfried Leibniz pada akhir abad ke-17. Melalui teorema fundamental kalkulus yang mereka kembangkan masing-masing, integral terhubung dengan diferensial: jika f adalah fungsi kontinu yang terdefinisi pada sebuah interval tertutup [a, b], maka, jika antiturunan F dari f diketahui, maka integral tertentu dari f pada interval tersebut dapat didefinisikan sebagai:

{\displaystyle \int _{a}^{b}\!f(x)\,dx=F(b)-F(a)\,}

Integral dan diferensial menjadi peranan penting dalam kalkulus, dengan berbagai macam aplikasi pada sains dan teknik.

Definisi formal – Integral Kalkulus

Ada beberapa cara untuk mendefinisikan integral.

Integral Riemann

Integral Riemann adalah konsep integral yang dasar. Definisi itu mudah dan berguna khususnya untuk fungsi-fungsi yang kontinu atau kontinu ‘titik demi titik’.

Integral Lebesgue

Integral Lebesgue merupakan suatu perumuman dari integral Riemann.

Mencari nilai integral

Substitusi

Contoh soal:
Cari nilai dari: {\displaystyle \int {\frac {lnx}{x}}\,dx\,}

{\displaystyle t=\ln x,dt={\frac {dx}{x}}}
{\displaystyle \int {\frac {lnx}{x}}\,dx\,=\int t\,dt}
{\displaystyle ={\frac {1}{2}}t^{2}+C}
{\displaystyle ={\frac {1}{2}}ln^{2}x+C}
{\displaystyle t=\ln x,dt={\frac {dx}{x}}}
{\displaystyle \int {\frac {lnx}{x}}\,dx\,=\int t\,dt}
{\displaystyle ={\frac {1}{2}}t^{2}+C}

Integrasi parsial

Integral parsial menggunakan rumus sebagai berikut:
Cara 1
{\displaystyle \int f'(x)g(x)\,dx=f(x)g(x)-\int f(x)g'(x)\,dx}
Contoh soal:
Cari nilai dari: {\displaystyle \int \ln x\,dx\,}

{\displaystyle f'(x)=1,f(x)=x,g(x)=lnx,g'(x)={\frac {1}{x}}\,}
Gunakan rumus di atas
{\displaystyle \int \ln x\ dx=xlnx-\int x{\frac {1}{x}}\,dx\,}
{\displaystyle =xlnx-\int 1\,dx\,}
{\displaystyle =xlnx-x+C\,}
Cara 2
TabelTurunanIntegral
+{\displaystyle g(x)}{\displaystyle \int f'(x)dx}
–{\displaystyle g'(x)}{\displaystyle f(x)}
+{\displaystyle g''(x)}
{\displaystyle \int f'(x)g(x)\,dx=f(x)g(x)-\int f(x)g'(x)\,dx}
Contoh soal:
Cari nilai dari: {\displaystyle \int \ln x\,dx\,}
TabelTurunanIntegral
+{\displaystyle lnx}{\displaystyle \int 1dx}
–{\displaystyle {\frac {1}{x}}}{\displaystyle x}
+{\displaystyle -{\frac {1}{x^{2}}}}{\displaystyle {\frac {1}{2}}x^{2}}
Gunakan rumus di atas
{\displaystyle \int \ln x\ dx=xlnx-{\frac {1}{x}}{\frac {1}{2}}x^{2}+C\,} (?)
{\displaystyle =xlnx-{\frac {1}{2}}x+C\,} (?)

Substitusi trigonometri

BentukGunakan
{\displaystyle {\sqrt {a^{2}-b^{2}x^{2}}}\,}{\displaystyle x={\frac {a}{b}}\sin \alpha \,}
{\displaystyle {\sqrt {a^{2}+b^{2}x^{2}}}\,}{\displaystyle \!\,x={\frac {a}{b}}\tan \alpha \,}
{\displaystyle {\sqrt {b^{2}x^{2}-a^{2}}}\,}{\displaystyle \,x={\frac {a}{b}}\sec \alpha \,}
Contoh soal:
Cari nilai dari: {\displaystyle \int {\frac {dx}{x^{2}{\sqrt {x^{2}+4}}}}\,}

{\displaystyle x=2\tan A,dx=2\sec ^{2}A\,dA\,}
{\displaystyle \int {\frac {dx}{x^{2}{\sqrt {x^{2}+4}}}}\,}
{\displaystyle =\int {\frac {2sec^{2}A\,dA}{(2tanA)^{2}{\sqrt {4+(2tanA)^{2}}}}}\,}
{\displaystyle =\int {\frac {2sec^{2}A\,dA}{4tan^{2}A{\sqrt {4+4tan^{2}A}}}}\,}
{\displaystyle =\int {\frac {2sec^{2}A\,dA}{4tan^{2}A{\sqrt {4(1+tan^{2}A)}}}}\,}
{\displaystyle =\int {\frac {2sec^{2}A\,dA}{4tan^{2}A{\sqrt {4sec^{2}A}}}}\,}
{\displaystyle =\int {\frac {2sec^{2}A\,dA}{4tan^{2}A.2secA}}\,}
{\displaystyle =\int {\frac {secA\,dA}{4tan^{2}A}}\,}
{\displaystyle ={\frac {1}{4}}\int {\frac {secA\,dA}{tan^{2}A}}\,}
{\displaystyle ={\frac {1}{4}}\int {\frac {cosA}{sin^{2}A}}\,dA\,}
Cari nilai dari: {\displaystyle \int {\frac {cosA}{sin^{2}A}}\,dA\,} dengan menggunakan substitusi
{\displaystyle t=sinA,dt=cosA\,dA\,}
{\displaystyle \int {\frac {cosA}{sin^{2}A}}\,dA\,}
{\displaystyle =\int {\frac {dt}{t^{2}}}\,}
{\displaystyle =\int t^{-2}\,dt\,}
{\displaystyle =-t^{-1}+C=-{\frac {1}{sinA}}+C\,}
Masukkan nilai tersebut:
{\displaystyle ={\frac {1}{4}}\int {\frac {cosA}{sin^{2}A}}\,dA\,}
{\displaystyle ={\frac {1}{4}}.-{\frac {1}{sinA}}+C\,}
{\displaystyle =-{\frac {1}{4sinA}}+C\,}
Nilai sin A adalah {\displaystyle {\frac {x}{\sqrt {x^{2}+4}}}}
{\displaystyle =-{\frac {1}{4sinA}}+C\,}
{\displaystyle =-{\frac {\sqrt {x^{2}+4}}{4x}}+C\,}

Integrasi pecahan parsial

Contoh soal:
Cari nilai dari: {\displaystyle \int {\frac {dx}{x^{2}-4}}\,}

{\displaystyle {\frac {1}{x^{2}-4}}={\frac {A}{x+2}}+{\frac {B}{x-2}}\,}
{\displaystyle ={\frac {A(x-2)+B(x+2)}{x^{2}-4}}\,}
{\displaystyle ={\frac {Ax-2A+Bx+2B}{x^{2}-4}}\,}
{\displaystyle ={\frac {(A+B)x-2(A-B)}{x^{2}-4}}\,}
Akan diperoleh dua persamaan yaitu {\displaystyle A+B=0\,} dan {\displaystyle A-B=-{\frac {1}{2}}}
Dengan menyelesaikan kedua persamaan akan diperoleh hasil {\displaystyle A=-{\frac {1}{4}},B={\frac {1}{4}}\,}
{\displaystyle \int {\frac {dx}{x^{2}-4}}\,}
{\displaystyle ={\frac {1}{4}}\int ({\frac {1}{x-2}}-{\frac {1}{x+2}})\,dx\,}
{\displaystyle ={\frac {1}{4}}(ln|x-2|-ln|x+2|)+C\,}
{\displaystyle ={\frac {1}{4}}ln|{\frac {x-2}{x+2}}|+C\,}

Integral Tak Tentu (antiderivatif)

Integral tak tentu atau antiturunan atau antiderivatif (bahasa Inggris: “indefinite integral” atau “antiderivative”) adalah suatu bentuk operasi pengintegralan suatu fungsi yang menghasilkan suatu fungsi baru. Fungsi ini belum memiliki nilai pasti (berupa variabel) sehingga cara pengintegralan yang menghasilkan fungsi tak tentu ini disebut “integral tak tentu”.

Bila fungsi F adalah integral tak tentu dari suatu fungsi f maka berlaku F’= f.

Proses untuk memecahkan antiderivatif adalah antidiferensiasi. Antiderivatif yang terkait dengan pasti integral melalui “Teorema dasar kalkulus”, dan memberikan cara mudah untuk menghitung integral dari berbagai fungsi.

Contoh Integral Tak Tentu (antiderivatif)

Penggunaan

Penentuan integral tentu. Bila fungsi F adalah integral tak tentu dari suatu fungsi f dan F’= f :

Rumus integrasi dasar

Umum

{\displaystyle \int x^{n}dx={\frac {1}{n+1}}x^{n+1}+C\,} ; n ≠ -1

Eksponen dan bilangan natural

{\displaystyle \int e^{x}dx=e^{x}+C\,}
{\displaystyle \int a^{x}dx={\frac {a^{x}}{lna}}+C\,} ; a ≠ 1 dan a > 0

Logaritma dan bilangan natural

{\displaystyle \int {\frac {1}{x}}dx=lnx+C}
{\displaystyle \int lnx\,dx=xlnx-x+C=xln\left({\frac {x}{e}}\right)+C}
{\displaystyle \int \log _{a}(x)\,dx=x\log _{a}(x)-{\frac {x}{\ln(a)}}+C=x\log _{a}\left({\frac {x}{e}}\right)+C}

Trigonometri

{\displaystyle \int \sin x\,dx=-\cos x+C\,}
{\displaystyle \int \cos x\,dx=\sin x+C\,}
{\displaystyle \int \tan x\,dx=\ln |\sec x|+C\,}
{\displaystyle \int \cot x\,dx=-\ln |\csc x|+C\,}
{\displaystyle \int \sec x\,dx=\ln |\sec x+\tan x|+C\,}
{\displaystyle \int \csc x\,dx=-\ln |\csc x+\cot x|+C\,}
{\displaystyle \int \sin ^{2}x\,dx={\frac {1}{2}}(x-\sin x\cos x)+C\,}
{\displaystyle \int \cos ^{2}x\,dx={\frac {1}{2}}(x+\sin x\cos x)+C\,}
{\displaystyle \int \tan ^{2}x\,dx=\tan x-x+C\,}
{\displaystyle \int \cot ^{2}x\,dx=-\cot x-x+C\,}
{\displaystyle \int \sec ^{2}x\,dx=\tan x+C\,}
{\displaystyle \int \csc ^{2}x\,dx=-\cot x+C\,}
{\displaystyle \int \sec x\tan x\,dx=\sec x+C\,}
{\displaystyle \int \csc x\cot x\,dx=-\csc x+C\,}
Invers
{\displaystyle \int {\frac {1}{\sqrt {1-x^{2}}}}\,dx=\arcsin x+C\,}
{\displaystyle \int {\frac {1}{1+x^{2}}}\,dx=\arctan x+C\,}
{\displaystyle \int {\frac {1}{x{\sqrt {x^{2}-1}}}}\,dx=\operatorname {arcsec} x+C\,}

Hiperbolik

{\displaystyle \int \sinh x\,dx=\cosh x+C\,}
{\displaystyle \int \cosh x\,dx=\sinh x+C\,}

Panjang busur

  • Sumbu x
{\displaystyle S=\int _{x_{1}}^{x_{2}}{\sqrt {1+(f(x))^{2}}}dx}
  • Sumbu y
{\displaystyle S=\int _{y_{1}}^{y_{2}}{\sqrt {1+(f(y))^{2}}}dy}

Luas daerah

Satu kurva

  • Sumbu x
{\displaystyle L=\int _{x_{1}}^{x_{2}}f(x)dx}
  • Sumbu y
{\displaystyle L=\int _{y_{1}}^{y_{2}}f(y)dy}

Dua kurva

  • Sumbu x
{\displaystyle L=\int _{x_{1}}^{x_{2}}(f(x_{2})-f(x_{1}))dx}
  • Sumbu y
{\displaystyle L=\int _{y_{1}}^{y_{2}}(f(y_{2})-f(y_{1}))dy}

atau juga {\displaystyle L={\frac {D{\sqrt {D}}}{6a^{2}}}}

Luas permukaan benda putar

  • Sumbu x
{\displaystyle L=2\pi \int _{x_{1}}^{x_{2}}f(x)ds}

dimana {\displaystyle ds={\sqrt {1+(f(x))^{2}}}dx}

  • Sumbu y
{\displaystyle L=2\pi \int _{y_{1}}^{y_{2}}f(y)ds}

dimana {\displaystyle ds={\sqrt {1+(f(y))^{2}}}dy}

Volume benda putar- Integral Kalkulus

Satu kurva

  • Sumbu x
{\displaystyle V=\pi \int _{x_{1}}^{x_{2}}(f(x))^{2}dx}
  • Sumbu y
{\displaystyle V=\pi \int _{y_{1}}^{y_{2}}(f(y))^{2}dy}

Dua kurva

  • Sumbu x
{\displaystyle V=\pi \int _{x_{1}}^{x_{2}}((f(x_{2}))^{2}-(f(x_{1}))^{2})dx}
  • Sumbu y
{\displaystyle V=\pi \int _{y_{1}}^{y_{2}}((f(y_{2}))^{2}-(f(y_{1}))^{2})dy}

Contoh Soal dan Jawaban Integral Kalkulus

  • Tentukan luas (tak tentu) dengan persamaan garis {\displaystyle y=x} dan batas-batas sumbu y dengan rumus integral!
{\displaystyle L=\int xdx}
{\displaystyle L={\frac {1}{2}}x^{2}} karena {\displaystyle y=x}
{\displaystyle L={\frac {1}{2}}xy}
  • Tentukan luas (tak tentu) dengan persamaan garis {\displaystyle y=x^{2}} dan batas-batas sumbu y dengan rumus integral!
{\displaystyle L=\int x^{2}dx}
{\displaystyle L={\frac {1}{3}}x^{3}} karena {\displaystyle y=x^{2}}
{\displaystyle L={\frac {1}{3}}xy}
  • Tentukan luas (tak tentu) dengan persamaan garis {\displaystyle y={\sqrt {x}}} dan batas-batas sumbu y dengan rumus integral!
{\displaystyle L=\int {\sqrt {x}}dx}
{\displaystyle L={\frac {2}{3}}x^{\frac {3}{2}}} karena {\displaystyle y={\sqrt {x}}}
{\displaystyle L={\frac {2}{3}}xy}
  • Buktikan luas persegi panjang {\displaystyle L=pl} dengan rumus integral!
Dengan posisi {\displaystyle y=p} dan titik (l,p)
{\displaystyle L=\int _{0}^{l}pdx}
{\displaystyle L=[px]_{0}^{l}}
{\displaystyle L=pl-0}
{\displaystyle L=pl}
  • Buktikan luas segitiga {\displaystyle L={\frac {at}{2}}} dengan rumus integral!
Dengan posisi {\displaystyle y={\frac {ax}{t}}} dan titik (t,a)
{\displaystyle L=\int _{0}^{t}{\frac {ax}{t}}dx}
{\displaystyle L=[{\frac {ax^{2}}{2t}}]_{0}^{t}}
{\displaystyle L={\frac {at^{2}}{2t}}-0}
{\displaystyle L={\frac {at}{2}}}
  • Buktikan volume tabung {\displaystyle V=\pi r^{2}t} dengan rumus integral!
Dengan posisi{\displaystyle y=r} dan titik (t,r)
{\displaystyle V=\pi \int _{0}^{t}(r)^{2}dx}
{\displaystyle V=\pi [r^{2}x]_{0}^{t}}
{\displaystyle V=\pi (r^{2}t-0)}
{\displaystyle V=\pi r^{2}t}
  • Buktikan volume kerucut {\displaystyle V={\frac {\pi r^{2}t}{3}}} dengan rumus integral!
Dengan posisi {\displaystyle y={\frac {rx}{t}}} dan titik (t,r)
{\displaystyle V=\pi \int _{0}^{t}({\frac {rx}{t}})^{2}dx}
{\displaystyle V=\pi [{\frac {r^{2}x^{3}}{3t^{2}}}]_{0}^{t}}
{\displaystyle V=\pi ({\frac {r^{2}t^{3}}{3t^{2}}}-0)}
{\displaystyle V={\frac {\pi r^{2}t}{3}}}
  • Buktikan volume bola {\displaystyle V={\frac {4\pi r^{3}}{3}}} dengan rumus integral!
{\displaystyle y={\sqrt {r^{2}-x^{2}}}} dan titik (-r,0) serta (r,0)
{\displaystyle V=\pi \int _{-r}^{r}({\sqrt {r^{2}-x^{2}}})^{2}dx}
{\displaystyle V=\pi \int _{-r}^{r}r^{2}-x^{2}dx}
{\displaystyle V=\pi [r^{2}x-{\frac {x^{3}}{3}}]_{-r}^{r}}
{\displaystyle V=\pi (r^{3}-{\frac {r^{3}}{3}}-(-r^{3}+{\frac {r^{3}}{3}}))}

Tabel Integral Kalkulus

Integral merupakan operasi dasar dalam kalkulus integral. Sementara diferensiasi mempunyai kaidah-kaidah mudah di mana turunan dari suatu fungsi yang rumit dapat dihitung dengan melakukan diferensiasi dari fungsi komponen yang lebih sederhana, integrasi tidak demikian, sehingga table dari integral yang sudah diketahui seringkali sangat berguna. Berikut adalah sejumlah antiderivatif yang paling umum

Artikel ini memberikan tabel operasi integrasi yang umum dijumpai. Pada daftar integrasi di bawah ini, C menyatakan konstanta sebarang.

Aturan integrasi dari fungsi-fungsi umum Integral Kalkulus

  1. {\displaystyle \int af(x)\,dx=a\int f(x)\,dx\qquad {\mbox{(}}a{\mbox{ konstan)}}\,\!}
  2. {\displaystyle \int [f(x)+g(x)]\,dx=\int f(x)\,dx+\int g(x)\,dx}
  3. {\displaystyle \int f(x)g(x)\,dx=f(x)\int g(x)\,dx-\int \left[f'(x)\left(\int g(x)\,dx\right)\right]\,dx}
  4. {\displaystyle \int [f(x)]^{n}f'(x)\,dx={[f(x)]^{n+1} \over n+1}+C\qquad {\mbox{(untuk }}n\neq -1{\mbox{)}}\,\!}
  5. {\displaystyle \int {f'(x) \over f(x)}\,dx=\ln {\left|f(x)\right|}+C}
  6. {\displaystyle \int {f'(x)f(x)}\,dx={1 \over 2}[f(x)]^{2}+C}

Integral fungsi sederhana

C sering digunakan untuk arbitrary constant of integration yang hanya dapat ditentukan jika suatu nilai integral pada beberapa titik sudah diketahui. Jadi setiap fungsi mempunyai jumlah antiderivatif tidak terbatas.

Rumus-rumus berikut hanya menyatakan dalam bentuk lain pernyataan-pernyataan dalam tabel turunan.

Fungsi rasional

{\displaystyle \int \,{\rm {d}}x=x+C}
{\displaystyle \int x^{n}\,{\rm {d}}x={\frac {x^{n+1}}{n+1}}+C\qquad {\mbox{ jika }}n\neq -1}
{\displaystyle \int {dx \over x}=\ln {\left|x\right|}+C}
{\displaystyle \int {dx \over {a^{2}+x^{2}}}={1 \over a}\arctan {x \over a}+C}

Fungsi irrasional

{\displaystyle \int {dx \over {\sqrt {a^{2}-x^{2}}}}=\sin ^{-1}{x \over a}+C}
{\displaystyle \int {-dx \over {\sqrt {a^{2}-x^{2}}}}=\cos ^{-1}{x \over a}+C}
{\displaystyle \int {dx \over x{\sqrt {x^{2}-a^{2}}}}={1 \over a}\sec ^{-1}{|x| \over a}+C}

Fungsi logaritma

{\displaystyle \int \ln {x}\,dx=x\ln {x}-x+C}
{\displaystyle \int \log _{b}{x}\,dx=x\log _{b}{x}-x\log _{b}{e}+C}

Fungsi eksponensial

{\displaystyle \int e^{x}\,dx=e^{x}+C}
{\displaystyle \int a^{x}\,dx={\frac {a^{x}}{\ln {a}}}+C}

Fungsi trigonometri

{\displaystyle \int \sin {x}\,dx=-\cos {x}+C}
{\displaystyle \int \cos {x}\,dx=\sin {x}+C}
{\displaystyle \int \tan {x}\,dx=\ln {\left|\sec {x}\right|}+C}
{\displaystyle \int \cot {x}\,dx=-\ln {\left|\csc {x}\right|}+C}
{\displaystyle \int \sec {x}\,dx=\ln {\left|\sec {x}+\tan {x}\right|}+C}
{\displaystyle \int \csc {x}\,dx=-\ln {\left|\csc {x}+\cot {x}\right|}+C}
{\displaystyle \int \sec ^{2}x\,dx=\tan x+C}
{\displaystyle \int \csc ^{2}x\,dx=-\cot x+C}
{\displaystyle \int \sec {x}\,\tan {x}\,dx=\sec {x}+C}
{\displaystyle \int \csc {x}\,\cot {x}\,dx=-\csc {x}+C}
{\displaystyle \int \sin ^{2}x\,dx={\frac {1}{2}}(x-\sin x\cos x)+C}
{\displaystyle \int \cos ^{2}x\,dx={\frac {1}{2}}(x+\sin x\cos x)+C}
{\displaystyle \int \sec ^{3}x\,dx={\frac {1}{2}}\sec x\tan x+{\frac {1}{2}}\ln |\sec x+\tan x|+C}
{\displaystyle \int \sin ^{n}x\,dx=-{\frac {\sin ^{n-1}{x}\cos {x}}{n}}+{\frac {n-1}{n}}\int \sin ^{n-2}{x}\,dx}
{\displaystyle \int \cos ^{n}x\,dx={\frac {\cos ^{n-1}{x}\sin {x}}{n}}+{\frac {n-1}{n}}\int \cos ^{n-2}{x}\,dx}
{\displaystyle \int \arctan {x}\,dx=x\,\arctan {x}-{\frac {1}{2}}\ln {\left|1+x^{2}\right|}+C}

Fungsi hiperbolik

{\displaystyle \int \sinh x\,dx=\cosh x+C}
{\displaystyle \int \cosh x\,dx=\sinh x+C}
{\displaystyle \int \tanh x\,dx=\ln |\cosh x|+C}
{\displaystyle \int {\mbox{csch}}\,x\,dx=\ln \left|\tanh {x \over 2}\right|+C}
{\displaystyle \int {\mbox{sech}}\,x\,dx=\arctan(\sinh x)+C}
{\displaystyle \int \coth x\,dx=\ln |\sinh x|+C}

Fungsi inversi hiperbolik

{\displaystyle \int \operatorname {arsinh} x\,dx=x\operatorname {arsinh} x-{\sqrt {x^{2}+1}}+C}
{\displaystyle \int \operatorname {arcosh} x\,dx=x\operatorname {arcosh} x-{\sqrt {x^{2}-1}}+C}
{\displaystyle \int \operatorname {artanh} x\,dx=x\operatorname {artanh} x+{\frac {1}{2}}\log {(1-x^{2})}+C}
{\displaystyle \int \operatorname {arcsch} \,x\,dx=x\operatorname {arcsch} x+\log {\left[x\left({\sqrt {1+{\frac {1}{x^{2}}}}}+1\right)\right]}+C}
{\displaystyle \int \operatorname {arsech} \,x\,dx=x\operatorname {arsech} x-\arctan {\left({\frac {x}{x-1}}{\sqrt {\frac {1-x}{1+x}}}\right)}+C}
{\displaystyle \int \operatorname {arcoth} \,dx=x\operatorname {arcoth} x+{\frac {1}{2}}\log {(x^{2}-1)}+C}

“Sophomore’s dream”

{\displaystyle {\begin{aligned}\int _{0}^{1}x^{-x}\,dx&=\sum _{n=1}^{\infty }n^{-n}&&(=1.29128599706266\dots )\\\int _{0}^{1}x^{x}\,dx&=-\sum _{n=1}^{\infty }(-n)^{-n}&&(=0.78343051071213\dots )\end{aligned}}}

diyakini berasal dari Johann Bernoulli.

Soal dan Jawaban

1. Diketahui turunan dari y = f(x) adalah  = f ‘(x) = 2x + 3.
Jika kurva y = f(x) melalui titik (1, 6), tentukan persamaan kurva tersebut.
Jawaban :
Diketahui f ‘(x) = 2x + 3.
Dengan demikian, y = f(x) = ʃ (2x + 3) dx = x2 + 3x + c.
Kurva melalui titik (1, 6), berarti f(1) = 6 sehingga dapat kita tentukan nilai c, yaitu 1 + 3 + c = 6 ↔ c = 2.
Jadi, persamaan kurva yang dimaksud adalah y = f(x) = x2 + 3x + 2.

2. Soal: Jika \displaystyle \int_{1}^{2} \frac{1}{\sqrt{x}+1} \, \mathrm{d}x = a, maka \displaystyle \int_{1}^{2} \frac{4\sqrt{x}+k}{\sqrt{x}+1} \, \mathrm{d}x = 4 - 3a  untuk nilai k =...

Jawaban:

Jawaban:

\begin{aligned} \int_{1}^{2} \frac{4\sqrt{x}+k}{\sqrt{x}+1} \, \mathrm{d}x &= 4 - 3a \\ \int_{1}^{2} \frac{4\sqrt{x} + 4 + k - 4}{\sqrt{x}+1} \, \mathrm{d}x &= 4 - 3 \int_{1}^{2} \frac{1}{\sqrt{x}+1} \, \mathrm{d}x \\ \int_{1}^{2} \frac{4 \left( \sqrt{x} + 1\right)}{\sqrt{x}+1} \, \mathrm{d}x + \int_{1}^{2} \frac{k - 4}{\sqrt{x}+1} &= 4 + \int_{1}^{2} \frac{-3}{\sqrt{x}+1} \, \mathrm{d}x \end{aligned}

Integral suku pertama di ruas kiri bernilai 4 sehingga

\begin{aligned} \quad k - 4 &= -3 \\ \quad \therefore \, k &= 1 \end{aligned}

3. Berapakah hasil dari integral ∫cos(2x−5)dx∫cos⁡(2x−5)dx ?

Jawaban:
Tulis u=2x−5u=2x−5
Maka du=2dx

Jadi

∫cos(2x−5)dx
=∫12cos u du
=12sin u+c
=12sin(2x−5)+c

4. Luas daerah yang dibatasi oleh kurva y = x^2, y = 1 dan x = 2 adalah…

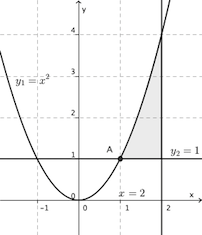
Soal kalkulus integral

Mencari koordinat titik potong A

\displaystyle \begin{aligned} y_1=y_2 \: \rightarrow \: x^2 = 1 \: \rightarrow A(1,1) \end{aligned}

Luas daerah yang diarsir ..

\displaystyle \begin{aligned} L_{\text{arsir}}=\int_1^2 \left(x^2-1\right)\:\mathrm{d}x \end{aligned}

5. Soal: Jika pada integral \displaystyle \int_{0}^{\frac{1}{2}} \frac{\sqrt{x}}{\sqrt{1-x}}\,\mathrm{d}x disubtitusikan \sqrt{x}=\sin y, maka menghasilkan…

Jawaban:

Dengan memisalkan \sqrt{x}=\sin y, didapat:

\displaystyle \begin{aligned} x &= \sin^2 y \\ \mathrm{d}x &=2\sin y \cos y \; \mathrm{d}y \end{aligned}

Pergantian batas integral

\displaystyle x=0 \rightarrow \sqrt{0} = \sin y \rightarrow y = 0
\displaystyle x=\frac{1}{2} \rightarrow \sqrt{\frac{1}{2}} = \sin y \rightarrow y = \frac{\pi}{4}

Sehingga bentuk integralnya menjadi :

\displaystyle \int _{ 0 }^{ \frac { \pi }{ 4 } } \frac{\sin y }{\sqrt{1-\sin^2y}}\cdot 2\sin y \cos y\; \mathrm{d}y
\displaystyle =2\int _{ 0 }^{ \frac { \pi }{ 4 } } \sin^2 y \; \mathrm{d}y ~~~\text{(misalkan : }y=x \text{)}
\displaystyle =2\int _{ 0 }^{ \frac { \pi }{ 4 } } \sin^2 x \; \mathrm{d}x

6. Soal: Jika pada integral \displaystyle \int_{0}^{\frac{1}{2}} \frac{\sqrt{x}}{\sqrt{1-x}}\,\mathrm{d}x disubtitusikan \sqrt{x}=\sin y, maka menghasilkan…

Dengan memisalkan \sqrt{x}=\sin y, didapat:

\displaystyle \begin{aligned} x &= \sin^2 y \\ \mathrm{d}x &=2\sin y \cos y \; \mathrm{d}y \end{aligned}

Pergantian batas integral

\displaystyle x=0 \rightarrow \sqrt{0} = \sin y \rightarrow y = 0
\displaystyle x=\frac{1}{2} \rightarrow \sqrt{\frac{1}{2}} = \sin y \rightarrow y = \frac{\pi}{4}

Sehingga bentuk integralnya menjadi :

\displaystyle \int _{ 0 }^{ \frac { \pi }{ 4 } } \frac{\sin y }{\sqrt{1-\sin^2y}}\cdot 2\sin y \cos y\; \mathrm{d}y
\displaystyle =2\int _{ 0 }^{ \frac { \pi }{ 4 } } \sin^2 y \; \mathrm{d}y ~~~\text{(misalkan : }y=x \text{)}
\displaystyle =2\int _{ 0 }^{ \frac { \pi }{ 4 } } \sin^2 x \; \mathrm{d}x

 7. Soal: \displaystyle \int \left( \sin x + \sin^3 x + \sin^5 + \dots \right) \, \mathrm{d}x = ...

Jawaban:

Bentuk dalam integral merupakan Deret Geometri tak hingga dengan suku pertama a = \sin xdan rasio r = \sin^2 x, sehingga bentuk integral tersebut dapat ditulis

\displaystyle \begin{aligned} \int \left( \sin x + \sin^3 x + \sin^5 + \dots \right) \, \mathrm{d}x &= \int \dfrac{\sin x}{1-\sin^2 x} \, \mathrm{d}x \end{aligned}

Dengan memisalkan u = \cos x \rightarrow -\mathrm{d}u = \sin x \, \mathrm{d}x dan mengganti 1 - \sin^2 x = \cos^2 x = u^2 maka

\displaystyle \begin{aligned} \int \dfrac{\sin x}{1-\sin^2 x} \, \mathrm{d}x &= \int \dfrac{1}{u^2} \, (-\mathrm{d}u) \\ &= u^{-1} + C \\ &= \sec x + C \\ \end{aligned}

8. Jika diketahui garis singgung parabola y=3x^2+ax+1, pada titik x=-2 membentuk sudut terhadap sumbu x sebesar \arctan(6). Luas daerah yang dibatasi oleh garis lurus y=-9x-59 dan parabola tersebut adalah…

Jawaban:

Garis singgung membentuk sudut terhadap sumbu x sebesar arctan(6)

\displaystyle \theta = \arctan{(6)} ~~~ \text{(dibaca sudut yang mempunyai nilai tan 6)} \\ \therefore \: \tan \theta = 6

Sehingga gradien garis singgung di x = -2

\displaystyle m= f'(-2) = \tan \theta = 6

Sedangkan f'(x) = y' = 6x + a, berarti

\displaystyle \begin{aligned} f'(-2) &= 6(-2) + a \\ 6 &= -12 + a \\ \therefore \: a &= 18 \: \rightarrow \: y = 3x^2 + 18x + 1 \end{aligned}

Daerah yang dibatasi y = 3x^2 + 18x + 1 dan y=-9x-59

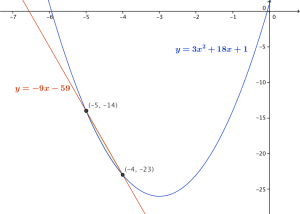
garis singgung parabola kalkulus

Titik potong kurva

\displaystyle \begin{aligned} 3x^2 + 18x + 1 &= -9x-59 \\ 3x^2 + 27x+60&=0 &\:(*)\\ x^2 + 9x + 20 &=0 \\ (x+5)(x+4)&=0 \rightarrow x_1 = -5 \: \cup \: x_2=-4 \end{aligned}

Luas daerah yang dibatasi y = 3x^2 + 18x + 1 dan y=-9x-59

\displaystyle \begin{aligned} L &= \int_{-5}^{-4} [(-9x-59)-(3x^2 + 18x + 1)] \: \mathrm{d}x \\ &= \int_{-5}^{-4} (-3x^2-27x-60) \: \mathrm{d}x \\ &= \left[-x^3 - \frac{27}{2}x^2 - 60x\right]_{-5}^{-4} \\ &= \left(-(-4)^3 - \frac{27}{2}(-4)^2 - 60(-4)\right) - \left(-(-5)^3 - \frac{27}{2}(-5)^2 - 60(-5)\right) \\ &= \frac{1}{2} \end{aligned}
Cara lain untuk menyelesaikan soal tersebut adalah:

Persamaan (*) mempunyai nilai diskriminan D = (27)^2 - 4(3)(60) = 9, sehingga luas daerah yang dibatasi y = 3x^2 + 18x + 1 dan y=-9x-59

\displaystyle \begin{aligned} L &= \frac{D\sqrt{D}}{6a^2} \\ &= \frac{9\sqrt{9}}{6(3)^2} \\ &= \frac{1}{2} \end{aligned}

catatan:
\boxed{\begin{array}{l} \text{Gradien garis singgung dititik }(x_1,y_1) \text{ pada fungsi }f(x) \\ \text{mempunyai gradien } m=f'(x_1) \end{array}}

\boxed{\begin{array}{l} \text{Nilai diskriminan dari persamaan kuadrat }y=ax^2+bx+c \\ D = b^2 - 4ac \end{array}}

9. Soal: Parabola ~y=x^2-2x+3m-1~ mempunyai titik puncak ~(p, q)~. Jika ~2p~ dan ~\dfrac{q}{4}~ dua suku pertama deret geometri tak hingga yang mempunyai jumlah 4, maka nilai ~m~ adalah…

Jawaban:

\displaystyle \begin{aligned} y&=x^2-2x+3m-1\\ y&=(x-1)^2+3m-2 \end{aligned}

Puncak parabola (p,q) \equiv (1, 3m-2)
Deret Geometri U_1=a=2p=2 dan U_2=\dfrac{q}{4}=\dfrac{3m-2}{4}

\displaystyle \begin{aligned} S_\infty&=\frac{a}{1-r}\\ 4&=\frac{2}{1-r} \\ r&=\frac{1}{2}\\ \frac{\frac{3m-2}{4}}{2}&=\frac{1}{2}\\ \therefore\:m&=2 \end{aligned}

catatan:
Fungsi kuadrat dengan titik puncak (x_p, y_p)
\boxed{~y=a(x-x_p)^2+y_p~}

Deret Geometri tak hingga konvergen dengan suku pertama a dan rasio r
\boxed{~S_\infty=\dfrac{a}{1-r}~}

Rasio deret geometri
\boxed{~r=\dfrac{U_1}{U_2}~}

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz |Matematika|IPA | Geografi & Sejarah|Info Unik|Lainnya | Business & Marketing

Pinter Pandai
«
»

Nilai Pi 1 juta digit pertama | Analisis dan…

PinterPandai
Mei 8, 2024 1 min read

Menghitung Dimensi Balok dari Luas Jaring-Jaringnya

Pinter Pandai
Apr 27, 2024 1 min read

Rumus Matematika dan Contoh untuk Penggunaan Sehari-hari

PinterPandai
Jul 17, 2023 6 min read

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *