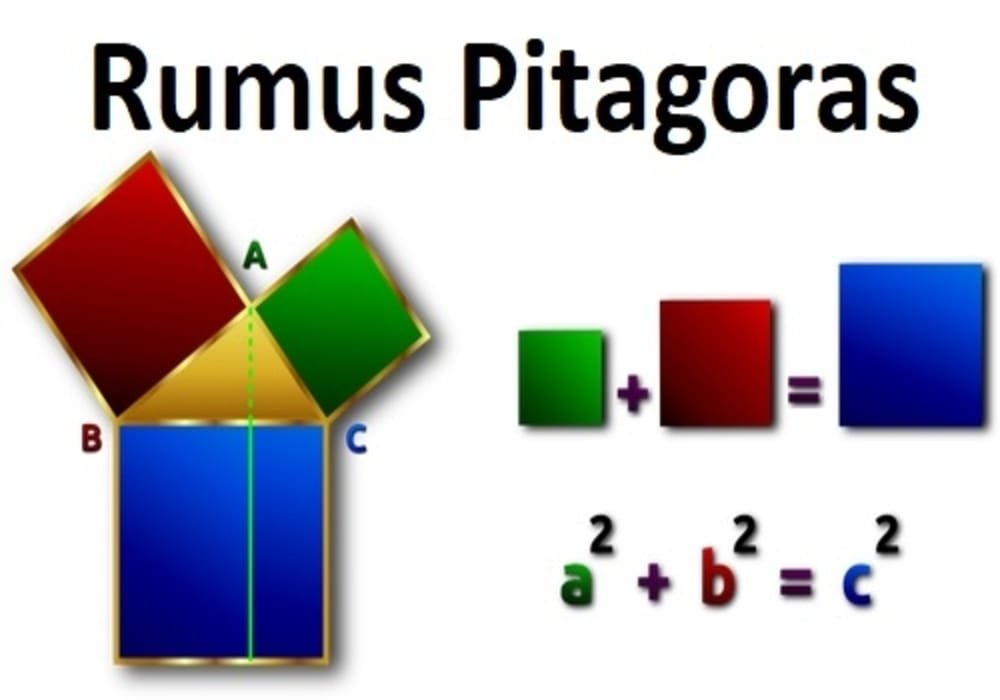
Rumus Segitiga Pythagoras
Rumus Pitagoras ini sering digunakan dalam penghitungan geometri, yakni ketika diminta untuk menghitung keliling bangun segitiga siku siku yang belum diketahui panjang sisi miringnya. Sebenarnya rumus Pythagoras sudah ada pada Matematika Sekolah Dasar (SD).
Tetapi karena sangat jarang bahkan hampir tidak ada soal yang secara langsung menanyakan atau memerintahkan untuk menentukan panjang sisi miring pada sebuah segitiga siku siku, mungkin inilah yang menyebabkan kita melupakan materi tentang pythagoras tersebut.
Teorema Phytagoras ini sangat terkenal dalam bidang geometri. Jugaterus dipakai pada tingkatan berikutnya. Misal pada materi dimensi tiga yang dipelajari pada jenjang SMA, begitu pula pada materi trigonometri.
Rumus Pitagoras:
a² + b² = c²
atau
b2 = a2 + c2
Maka untuk menghitung sisi tegak dan sisi mendatarnya berlaku rumus berikut :
a2 = b2 – c2
c2 = b2 – a2
Rumus Pythagoras dalam bentuk akar, jika :
- Sisi miringnya c
- Sisi tegak dan mendatarnya ialah a dan b
Rumus pitagoras bentuk akar
a = √ c² – b²
b = √ c² – a²
c = √ a² + b²

Rumus Pitagoras Dalam Bentuk Akar Kuadrat
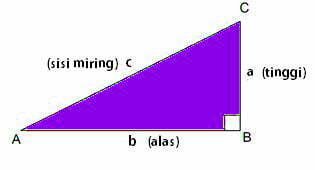
b² = c² – a²
Rumus untuk mencari sebuah sisi samping/tinggi segitiga:
a² = c² – b²
Rumus untuk mencari sebuah sisi miring segitiga siku-siku:
c² = a² + b²
Catatan : Rumus pythagoras, hanya berlaku pada segitiga siku – siku saja.
Dalam dalil atau teorema pythagoras, ada pola angka yang perlu untuk diingat supaya dalam menyelesaikan soal pythagoras akan lebih mudah dan cepat dalam mengerjakannya, pola tersebut adalah sebagai berikut :
- a – b – c
- 3 – 4– 5
- 5 – 12– 13
- 6 – 8– 10
- 7 – 24– 25
- 8 – 15– 17
- 9 – 12– 15
- 10 – 24– 26
- 12 – 16– 20
- 14 – 48– 50
- 15 – 20– 25
- 15 – 36– 39
- 16 – 30– 34
Keterangan :
a = tinggi segitiga
b = alas segitiga
c = sisi miring
Teorema Pitagoras (Phytagoras)
Berdasarkan rumus tersebut terbukti bahwa sisi miring sebuah segitiga siku – siku ialah akar dari jumlah kuadrat sisi – sisi yang lain.
- a ialah sisi alas (horizontal)
- b ialah sisi tinggi (vertikal)
- c ialah sisi miring
Untuk lebih jelasnya perhatikan gambar di bawah ini :
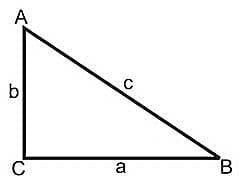 Segitiga Siku – Siku
Segitiga Siku – SikuSegitiga di atas adalah segitiga siku-siku yang mempunyai satu sisi tegak (BC),satu sisi mendatar (AB)dan satu sisi miring (AC). Dalil phytagoras atau rumus phytagoras berguna untuk mencari salah satu sisi dengan kedua sisi diketahui.

Sumber foto: Free SVG
Pernyataan Teorema Pitagoras (Pythagoras)
Teorema Pitagoras (Pythagoras) menyatakan bahwa:
1. Jumlah luas bujur sangkar pada kaki sebuah segitiga siku-siku sama dengan luas bujur sangkar di hipotenus.
2. Sebuah segitiga siku-siku adalah segitiga yang mempunyai sebuah sudut siku-siku; kaki-nya adalah dua sisi yang membentuk sudut siku-siku tersebut, dan hipotenus adalah sisi ketiga yang berhadapan dengan sudut siku-siku tersebut. Pada gambar di bawah ini, a dan b adalah kaki segitiga siku-siku dan c adalah hipotenus:
3. Pythagoras menyatakan teorema ini dalam gaya goemetris, sebagai pernyataan tentang luas bujur sangkar:
- Jumlah luas bujur sangkar biru dan merah sama dengan luas bujur sangkar ungu.
- Akan halnya, Sulbasutra India juga menyatakan bahwa:
- Tali yang direntangkan sepanjang panjang diagonal sebuah persegi panjang akan menghasilkan luas yang dihasilkan sisi vertikal dan horisontalnya. Menggunakan aljabar, kita dapat mengformulasikan ulang teorema tersebut ke dalam pernyataan modern dengan mengambil catatan bahwa luas sebuah bujur sangkar adalah pangkat dua dari panjang sisinya:
4. Jika sebuah segitiga siku-siku mempunyai kaki dengan panjang a dan b dan hipotenus dengan panjang c, maka a+ b = c.
Hipotenusa
Panjang hipotenusa dari segitiga siku-siku dapat ditentukan menggunakan teorema Pythagoras, yang menyatakan bahwa kuadrat panjang hipotenusa sama dengan jumlah kuadrat panjang dari dua sisi lainnya.
Rumus untuk mencari garis hipotenusa, yaitu:
Keterangan:
= garis hipotenusa
Contoh Soal Pitagoras dan Jawabannya
1. Suatu segitiga siku- siku mempunyai sisi tegak (AB) panjangnya 15 cm dan sisi mendatarnya (BC) 8 cm, Berapakah cm kah sisi miring (AC) ?
Penyelesaian :
Diketahui :
- AB =15
- BC =8
Ditanya : Panjang AC …?
Jawaban :
Cara Pertama :
AC² = AB² + BC²
AC² =152² + 82²
AC² =225 + 64
AC² =289
AC = √289
AC =17
Cara Kedua :
AC =√ AB² + BC²
AC =√ 152 + 82
AC =√ 255 + 64
AC =√ 289
AC =17
Maka, panjang AC adalah 17 cm
2. Berapakah panjang sisi tegak suatu segitiga siku – siku apabila diketahui panjang sisi miringnya 13 cm dan sisi datarnya adalah 5 cm ?
Penyelesaian :
Misalnya : c = sisi miring, b = sisi datar, a = sisi tegak
Diketahui :
- c = 13 cm
- b = 5 cm
Ditanya : a = …?
Jawaban :
Cara Pertama :
a² = c² – b²
a² = 132 – 52
a² = 169 – 25
a² = 144
a = √ 144
a = 12
Cara Kedua :
a =√ c² – b²
a =√ 132 – 52
a =√ 169 – 25
a =√ 144
a =12
Maka, panjang sisi tegak segitiga tersebut adalah 12 cm
3. Ada sbuah segitiga ABC , siku – siku di B, apabila panjang AB = 16 cm dan BC = 30 , maka berapakah panjang sisi miring segitiga ( AC ) ?
Penyelesaian :
Diketahui :
- AB =16
- BC =30
Ditanya : AC =…?
Jawaban :
AC =√ AB² + BC²
AC =√ 16 2 + 302
AC = √ 256 + 900
AC =√ 1156
AC =34
Maka, panjang AC adalah 34 cm
4. Sebuah taman berbentuk setitiga siku-siku dengan panjang sisinya masing-masing 3m, 4m, 5m. Jika separuh luas taman akan ditutup tegel keramik, dengan harga paving tiap meter perseginya Rp 100.000,00. Butuh biaya berapa untuk pemasangan tegel keramik yang menutup taman tersebut?
Jawab:
Untuk mengetahui separuh luas tegel keramik yang akan dipasang, maka kita perlu tahu luas setengah setiga siku-siku tersebut. Dengan demikian:
L= ½ luas setiga siku-siku=½ x ½ x a x t
L=1/4 x 4x 3= 3 m2
Biaya total yang dibutuhkan = Rp 100.000,00 x 3 = Rp 300.000,00
Jadi untuk memagari pinggiran taman dibutuhkan biaya sebesar Rp 300.000,00
5. Diketahui luas dari sebuah segitiga yang panjang alasnya 24 cm adalah 180 cm2. Hitunglah tinggi dari segitiga tersebut!
Jawaban:
Luas Segitiga = ½ x alas x tinggi
180 cm2= ½ x 24 cm x tinggi
180 cm2= 12 cm x tinggi
tinggi = 180 cm2/12 cm
tinggi = 15 cm.
6. Panjang sisi miring dan alas segitiga siku-siku berturut-turut adalah 20 cm dan 24 cm. Berapakah luas segitiga tersebut?
20² = t² + 12² → 12 berasal dari ½ panjang alas
t² = 20² – 12²
t² = 400 – 144
t² = 256
t = √256
t = 16 cm
L = ½ x 24 x 16 = 192 cm²
7. Pak Willy mengintari pinggiran lapangan berbentuk persegi panjang dua kali putaran penuh dan menempuh jarak 600 m. Jika lebar lapangan 50 m. Berapa luas lapangan tersebut?
Jawaban:
Untuk mencari luas lapangan, kita perlu tahu ukuran lapangan. Karena panjang lapangan belum diketahui, maka kita cari panjang lapangan dulu dengan konsep keliling yang sudah kita pelajari.
Karena mengelilingi dua kali putaran penuh, maka keliling lapangan 600m/2= 300 m.
Maka K=2p+2l
300=2p+2.50
300=2p+100
2p=200, maka p= 100m.
Jadi panjang lapangan 100m.
Dengan demikian luas lapangan= px l= 100 x 50= 500m2
8. Sebuah segitiga DEF yang merupakan segitiga sama sisi memiliki luas 25√3 cm², hitunglah berapa kelilingnya?
Penyelesaian :
Diketahui: luas = 25√3 cm²
Ditanya: keliling ?
Jawaban:
Luas = (a²/4)√3
25√3= (a²/4)√3 (√3 di ruas kanan dan ruas kiri bisa kita coret)
25 = a²/4
100 = a²
a = √100
a = 10 cm
Keliling = 3a
Keliling = 3.10
Keliling = 30 cm.
9. Diketahui segitiga ABC siku-siku di B. Jika Luasnya 150 cm² dan panjang AB 20 cm, hitunglah keliling segitiga tersebut!
Berdasarkan soal tersebut, AC adalah sisi miring segitiga.
L = ½ x AB x BC
150 = ½ x 20 x BC
150 : ½ = 20 x BC
300 = 20 x BC
BC = 300/20
BC = 15 cm
AC² = AB² + BC²
AC² = 20² + 15²
AC² = 400 + 225
AC² = 625
AC = √625
AC = 25 cm
K = AB + BC + AC = 20 + 15 + 25 = 60 cm
10. Berikut ini adalah ukuran sisi-sisi dari empat buah segitiga:
1. 3 cm, 4 cm, 5 cm
2. 7 cm, 8 cm, 9 cm
3. 5 cm, 12 cm, 15 cm
4. 7 cm, 24 cm, 25 cm
Segitiga yang berbentuk segitiga siku-siku ditunjukkan oleh nomor…
A. 1 dan 2 C. 2 dan 3
B. 1 dan 3 D. 1 dan 4
Apabila 3 bilangan yang mewakili panjang sisi segitiga memenuhi rumus Pythagoras a2+b2=c2 dengan c sebagai panjang sisi terpanjang (hipotenusa), maka segitiga itu merupakan segitiga siku-siku.
Cek pernyataan 1:
32+42=9+16=25=52
(Segitiga siku-siku)
Cek pernyataan 2:
72+82=49+64=113>92=81
(Bukan segitiga siku-siku melainkan segitiga lancip)
Cek pernyataan 3:
52+122=25+144=169<152=225
(Bukan segitiga siku-siku melainkan segitiga tumpul)
Cek pernyataan 4:
72+242=49+576=625=252
(Segitiga siku-siku)
Jadi, segitiga yang berbentuk segitiga siku-siku ditunjukkan oleh nomor 1 dan 4 (Jawaban D).
Bacaan Lainnya
- Linear Aljabar – Persamaan Linear dengan Matriks, Homogen, Matriks Diagonal, Segitiga, dan Simetris, Transpos Matriks, Determinan, Adjoint Matriks (Orde 3×3), Matriks Balikan (Invers), Penyelesaian Persamaan Linear dengan Matriks (Bagian 2), Vektor dalam Ruang Euklidian – Bersama Contoh Soal dan Jawaban
- Rumus segitiga siku-siku – Contoh Soal dan Jawaban – Test Matematika: Mana yang lebih luas? A atau B
- Rumus Diferensial (Turunan Fungsi) – Beserta Contoh Soal dan Jawaban
- Berapa Kecerdasan IQ Anda? Tes IQ Anda Disini
- 10 Kebiasaan Baik Yang Dapat Mengasah Otak Menjadi Lebih Efektif
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
- Tulisan Menunjukkan Kepribadian Anda & Bagaimana Cara Anda Menulis?
- Top 10 Sungai Terpanjang Di Dunia
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “oooh begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Math is Fun, Vedantu, Monterey Institute, Math Planet
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing