PINTERpandai
Pinter Pandai

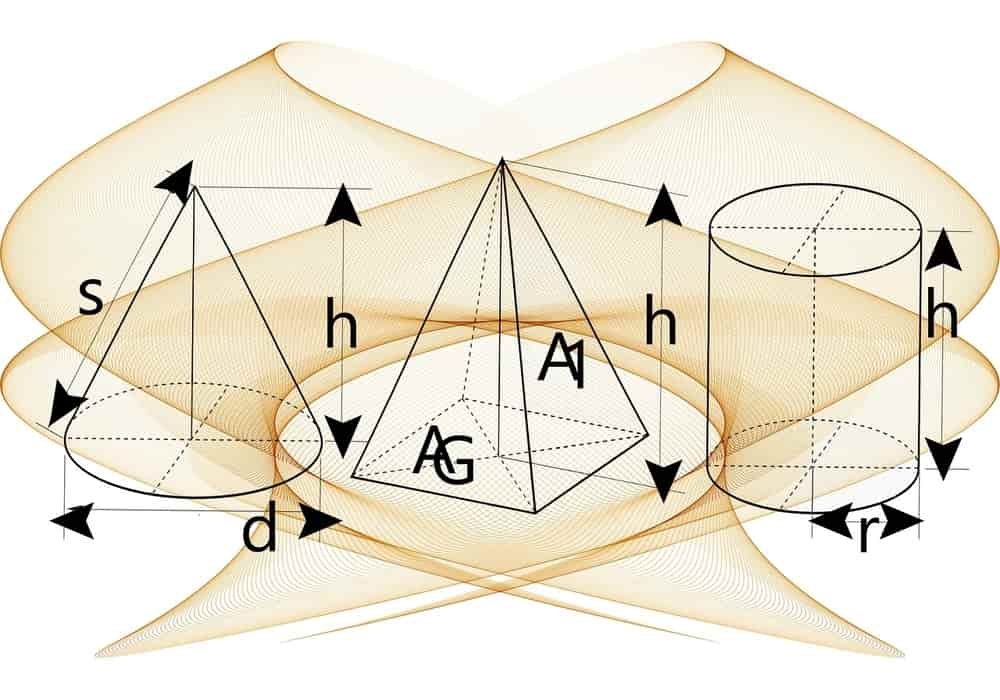
Rumus Geometri – Contoh Soal dan Jawaban – Segi tiga, Persegi, Trapesium, Layang-layang, Jajaran Genjang, Belah ketupat, Lingkaran, Prisma, Balok, Kubus, Tabung, Limas, Bola

4 min read

Rumus geometri

Rumus-Rumus Geometri

Geometri merupakan cabang matematika yang bersangkutan dengan pertanyaan bentuk, ukuran, posisi relatif gambar dan sifat ruang. Dibawah ini adalah rumus geometri lengkap.

Geometri awal. Catatan paling awal mengenai geometri dapat ditelusuri hingga ke zaman Mesir kuno, peradaban Lembah Sungai Indus dan Babilonia. Peradaban-peradaban ini diketahui memiliki keahlian dalam drainase rawa, irigasi, pengendalian banjir dan pendirian bangunan-bagunan besar. Kebanyakan geometri Mesir kuno dan Babilonia terbatas hanya pada perhitungan panjang ruas-ruas garis, luas dan volume.

Rumus geometri
Rumus Geometri: kerucut limas silinder – Geometri dalam bahasa Yunani Kuno: γεωμετρία, geo-“bumi”,-metron “pengukuran”. Sumber foto: Pixabay

Rumus Geometri bangun datar

Rumus Bangun Datar

  • Rumus Persegi

Luas = s x s = s2 ( Luas = ½ x diagonal (d) 1 x diagonal (d) 2, ‘sudah dibuktikan’ )
Keliling = 4 x s
dengan s = panjang sisi persegi
  • Rumus Persegi Panjang
Luas = p x l
p = Luas : lebar
l = Luas : panjang
Keliling = 2p + 2l = 2 x (p + l)
dengan p = panjang persegi panjang, dan l = lebar persegi panjang

  • Rumus Segitiga

Luas = ½ x a x t
dengan a = panjang alas segitiga, dan t = tinggi segitiga
Panjang sisi miring segitiga siku-siku dicari dengan rumus Phytagoras (A2 + B2 = C2)

  • Rumus Jajar Genjang

Luas = a x t
dengan a = panjang alas jajargenjang, dan t = tinggi jajargenjang

  • Rumus Trapesium

Luas = ½ x (s1 + s2) x t
dengan s1 dan s2 = sisi-sisi sejajar pada trapesium, dan t = tinggi trapesium

  • Rumus Layang-layang

Luas = ½ x diagonal (d) 1 x diagonal (d) 2

  • Rumus Belah Ketupat

Luas = ½ x diagonal (d) 1 x diagonal (d) 2

  • Rumus Lingkaran

Luas = π (pi) x jari-jari (r) 2
        = πr2
{\displaystyle L=\pi \times r^{2}}dengan

{\displaystyle L} adalah Luas lingkaran,

\pi  adalah {\displaystyle {\frac {22}{7}}} jika jari-jarinya kelipatan 7 atau {\displaystyle 3.14} jika jari-jarinya bukan kelipatan 7

{\displaystyle r} adalah jari-jari lingkaran

Jajaran genjang (rumus geometri) 

Jajar genjang
dengan alas {\displaystyle a} dan tinggi {\displaystyle t}

Jajar genjang atau Jajaran genjang (inggris parallelogram) adalah bangun datar dua dimensi yang dibentuk oleh dua pasang rusuk yang masing-masing sama panjang dan sejajar dengan pasangannya, dan memiliki dua pasang sudut yang masing-masing sama besar dengan sudut di hadapannya.

Jajar genjang dengan empat rusuk yang sama panjang disebut belah ketupat.

Rumus jajar genjang

Keliling

{\displaystyle K=2\cdot alas+2\cdot sisimiring}

Luas

{\displaystyle L=Alas\cdot tinggi}

Trapesium (rumus geometri)

Trapesium siku-siku dan trapesium biasa dengan tinggi {\displaystyle t}

Trapesium adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang dua di antaranya saling sejajar namun tidak sama panjang.

Trapesium termasuk jenis bangun datar segi empat.

Trapesium yang rusuk ketiganya tegak lurus terhadap rusuk-rusuk sejajar disebut trapesium siku-siku.

Jenis-jenis trapesium dalam rumus geometri

Trapesium terdiri dari 3 jenis, yaitu:

  1. Trapesium sembarang, yaitu trapesium yang keempat rusuknya tidak sama panjang. Trapesium ini tidak memiliki simetri lipat dan hanya memiliki 1 simetri putar.
  2. Trapesium sama kaki, yaitu trapesium yang mempunyai sepasang rusuk yang sama panjang, di samping mempunyai sepasang rusuk yang sejajar. Trapesium ini memiliki 1 simetri lipat dan 1 simetri putar.
  3. Trapesium siku-siku, yaitu trapesium yang mana dua di antara keempat sudutnya merupakan sudut siku-siku. Rusuk-rusuk yang sejajar tegak lurus dengan tinggi trapesium ini. Trapesium ini tidak memiliki simetri lipat dan hanya memiliki satu simetri putar.

Rumus trapesium

Keliling

{\displaystyle K=AB+BC+CD+DA}

Luas

{\textstyle L={\frac {{\text{Jumlah rusuk sejajar}}\times {\text{tinggi}}}{2}}\ }

Layang-layang (rumus geometri)

Layang-layang
dengan rusuk {\displaystyle s} dan diagonal {\displaystyle d}

Layang-layang adalah bangun datar dua dimensi yang dibentuk oleh dua pasang rusuk yang masing-masing pasangannya sama panjang dan saling membentuk sudut.

Layang-layang dengan keempat rusuk yang sama panjang disebut belah ketupat.

Rumus Layang-layang

Keliling

{\displaystyle K=2\cdot s_{1}+2\cdot s_{2}}

Luas

{\displaystyle L={\tfrac {1}{2}}\cdot d_{1}\cdot d_{2}}

Belah ketupat (rumus geometri) 

Belah ketupat
dengan rusuk {\displaystyle s} dan diagonal {\displaystyle d}

Belah ketupat (inggris rhombus) adalah bangun datar dua dimensi yang dibentuk oleh empat buah rusuk yang sama panjang, dan memiliki dua pasang sudut bukan siku-sikuyang masing-masing sama besar dengan sudut di hadapannya.

Belah ketupat dapat dibangun dari dua buah segitiga sama kaki identik yang simetri pada alas-alasnya.

Rumus belah ketupat

Keliling

{\displaystyle K=4\cdot s}

Luas

{\displaystyle L={\tfrac {1}{2}}\cdot d1\cdot d2}

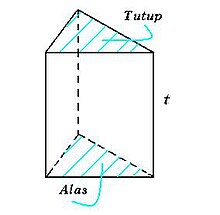
Prisma (rumus geometri)

Sebuah prisma segitiga dengan tinggi t

Dalam geometri, prisma adalah bangun ruang tiga dimensi yang dibatasi oleh alas dan tutup identik berbentuk segi-n dan sisi-sisi tegak berbentuk persegi atau persegi panjang. Dengan kata lain prisma adalah bangun ruang yang mempunyai penampang melintang yang selalu sama dalam bentuk dan ukuran. Prisma segi-n memiliki n + 2 sisi, 3n rusuk dan 2n titik sudut.

Prisma dengan alas dan tutup berbentuk persegi disebut balok sedangkan prisma dengan alas dan tutup berbentuk lingkaran disebut tabung.

Rumus Prisma

Luas permukaan

Luas permukaan prisma dengan alas dan tutup segi-n dapat dihitung dengan rumus berikut:

{\displaystyle L=2\cdot L_{\text{alas}}+K_{\text{alas}}\cdot t}

Volume

{\displaystyle V=L_{\text{alas}}\cdot t}

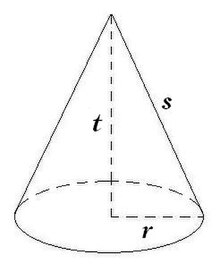
Kerucut (rumus geometri) 

Sebuah kerucut dengan tinggi t dan garis pelukis s

Dalam geometri, kerucut adalah sebuah limas istimewa yang beralas lingkaran. Kerucut memiliki 2 sisi dan 1 rusuk.

Sisi tegak kerucut tidak berupa segitiga tapi berupa bidang miring yang disebut selimut kerucut.

Rumus kerucut

Luas alas

{\displaystyle L=\pi r^{2}}

Luas selimut

{\displaystyle L=\pi rs}

Luas permukaan

{\displaystyle L=\ LuasLingkaran+LuasSelimut}
{\displaystyle =\pi r^{2}+\pi rs}, atau
{\displaystyle =\pi r\cdot (r+s)}

Volume

{\displaystyle V={\frac {1}{3}}\cdot \pi r^{2}\cdot t}

Kubus (rumus geometri)

Kubus

Kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang kongruen berbentuk bujur sangkar. Kubus memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Kubus juga disebut bidang enam beraturan, selain itu juga merupakan bentuk khusus dalam prisma segiempat.

Rumus Kubus

Bila variabel S adalah panjang rusuk kubus, maka:

Luas permukaan

{\displaystyle L=6\cdot S^{2}}

Volume

{\displaystyle V=\ S^{3}}

Diagonal sisi

{\displaystyle D_{Ss}=S{\sqrt {2}}}

Diagonal sisi seluruhnya

{\displaystyle D_{Ss}=12\cdot S{\sqrt {2}}}

Diagonal ruang

{\displaystyle D_{R}=S{\sqrt {3}}}

Diagonal ruang seluruhnya

{\displaystyle D_{Rs}=4\cdot S{\sqrt {3}}}

Luas bidang diagonal

{\displaystyle B_{D}=S^{2}{\sqrt {2}}}

Luas bidang diagonal seluruhnya

{\displaystyle B_{Ds}=6\cdot S^{2}{\sqrt {2}}}

Contoh-contoh soal dan jabawan Kubus, mohon klik disini.

Tabung (rumus geometri)

Sebuah tabung

Dalam geometri, tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaranidentik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut. Tabung memiliki 3 sisi dan 2 rusuk.

Kedua lingkaran disebut sebagai alas dan tutup tabung serta persegi panjang yang menyelimutinya disebut sebagai selimut tabung.

Rumus tabung (silinder)

{\displaystyle r=r_{\text{alas}}}
{\displaystyle t=h/_{\text{tinggi}}}
{\displaystyle d=d_{\text{alas}}}

Luas alas

{\displaystyle L=\pi r^{2}}

Luas selimut

{\displaystyle L=2\pi rt}

Luas permukaan

{\displaystyle L=\ L_{\text{alas}}+L_{\text{selimut}}}
{\displaystyle =\pi d(r+t)}
{\displaystyle =2\cdot \pi r^{2}+2\pi r\cdot t\,}, atau
{\displaystyle =2\cdot \pi r\cdot (r+t)}

Luas permukaan tanpa tutup

{\displaystyle L=\ L_{\text{alas}}+L_{\text{selimut}}}
{\displaystyle =\pi r^{2}+2\pi r\cdot t}
{\displaystyle =\pi r(r+2\cdot t)}

Volume

{\displaystyle V=\pi r^{2}\cdot t}
{\displaystyle ={\frac {1}{4}}\pi d^{2}\cdot t}

Klik disini untuk mengetahui lebih lanjut tentang rumus tabung dan contoh soal beserta jawabannya.

Limas (rumus geometri)

Sebuah limas segi empat dengan tinggi t

Dalam geometri, limas adalah bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga. Limas memiliki n + 1 sisi, 2n rusuk dan n + 1 titik sudut.

Kerucut dapat disebut sebagai limas dengan alas berbentuk lingkaran.

Limas dengan alas berupa persegi disebut juga piramida.

Rumus limas

Luas Permukaan Limas

L = luas alas + luas selubung limas

= Luas alas + 1/4 × Keliling alas × t segitiga

Volume

{\displaystyle V={\frac {1}{3}}\cdot LuasAlas\cdot t}

Nama Limas
Sisi
Rusuk
Titik Sudut
Limas Segitiga
4
6
4
Limas Segiempat
5
8
5
Limas Segilima
6
10
6
Limas Segienam
7
12
1

Klik disini untuk membaca lebih lanjut tentang rumus limas beserta contoh soal dan jawaban.

Bola (rumus geometri)

Bangun bola
dengan jari-jari {\displaystyle r}

Dalam geometri, bola adalah bangun ruang tiga dimensi yang dibentuk oleh tak hinggalingkaran berjari-jari sama panjang dan berpusat pada satu titik yang sama. Bola hanya memiliki 1 sisi.

Rumus bola

Luas permukaan

{\displaystyle L=4\pi r^{2}\,}

Volume

{\displaystyle V={\frac {4}{3}}\pi r^{3}}

Klik disini untuk mengetahui lebih lanjut tentang rumus bola dan contoh soal beserta jawabannya.

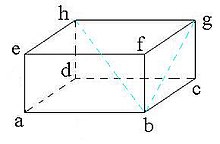
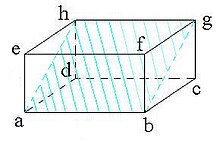
Balok (rumus geometri)

Balok adalah bangun ruang tiga dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang, dengan paling tidak satu pasang di antaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok yang dibentuk oleh enam persegi sama dan sebangun disebut sebagai kubus.

Elemen balok

  • Panjang {\displaystyle (p)} adalah rusuk terpanjang dari alas balok.
  • Lebar {\displaystyle (l)} adalah rusuk terpendek dari sisi alas balok.
  • Tinggi {\displaystyle (t)} adalah rusuk yang tegak lurus terhadap panjang dan lebar balok.

Rumus balok

Diagonal Ruang b-h dan
Diagonal Bidang b-g

Bidang Diagonal a-b-g-h

Luas permukaan balok

{\displaystyle L=2\cdot (p\cdot l+p\cdot t+l\cdot t)}

Volume balok

{\displaystyle V=p\cdot l\cdot t}

Panjang diagonal ruang balok

{\displaystyle d_{R}={\sqrt {(p^{2}+l^{2}+t^{2})}}}

Panjang diagonal bidang balok

{\displaystyle d_{B1}={\sqrt {(s^{2}+s^{2})}}}
{\displaystyle d_{B2}={\sqrt {(s^{2}+s^{2})}}}
{\displaystyle d_{B3}={\sqrt {(s^{2}+s^{2})}}}

Luas bidang diagonal balok

{\displaystyle L_{B1}=d_{B1}\cdot t}
{\displaystyle L_{B2}=d_{B2}\cdot l}
{\displaystyle L_{B3}=d_{B3}\cdot p}

Klik disini untuk mengetahui lebih lanjut tentang rumus balok dan contoh soal beserta jawabannya.

Rumus geometri
Rumus Geometri: kerucut limas silinder – Geometri dalam bahasa Yunani Kuno: γεωμετρία, geo-“bumi”,-metron “pengukuran”. Sumber foto: Pixabay

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: CleverlySmart, Wikipedia, Pioneer Mathematics

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing

Pinter Pandai
«
»

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

PinterPandai
Okt 14, 2024 58 sec read

Tes matematika logika: Jika 4 + 3 = 27,…

PinterPandai
Okt 9, 2024 1 min read

Nilai Pi 1 juta digit pertama | Analisis dan…

PinterPandai
Mei 8, 2024 1 min read

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *