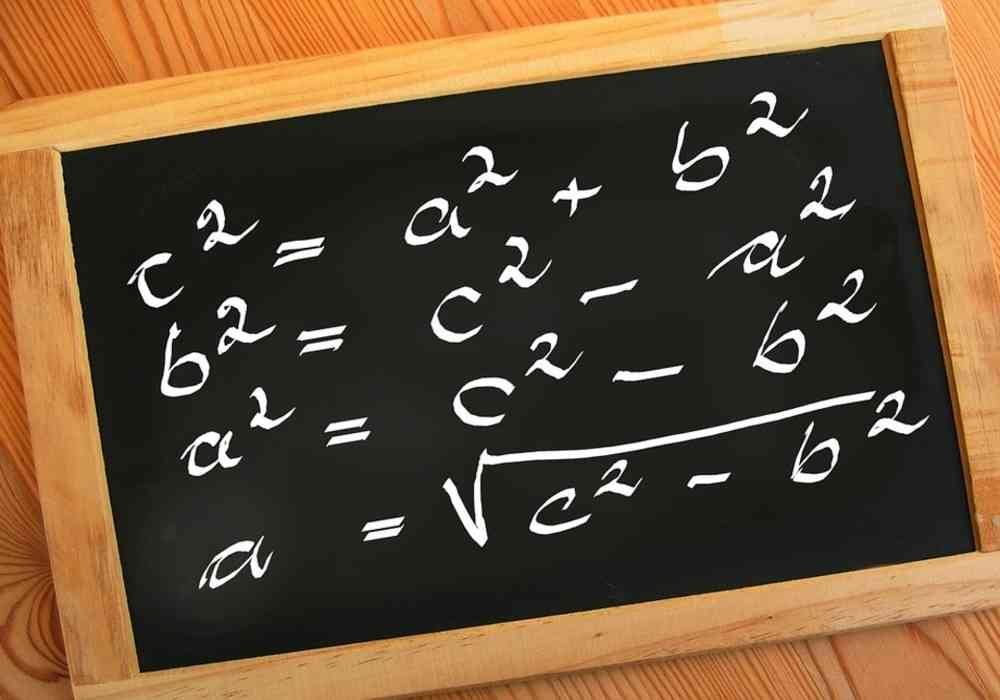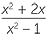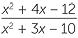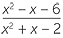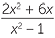Akar Kuadrat Adalah

Sebuah perhitungan matematika aljabar dari sebuah faktor angka dengan cara meng-kuadratkan yang menghasilkan angka tersebut (disebut sebagai akar kuadrat).

Di dalam matematika, akar kuadrat dari bilangan x sama dengan bilangan r sedemikian sehingga r² = x, atau, di dalam perkataan lain, bilangan r yang bila dikuadratkan sama dengan x.

Cara Menghitung Akar Kuadrat Dengan Faktorisasi

Berapakah akar dari 64
64 = 2 x 32 = 2 x 2 x 16 = 4 x 16
Maka
akar 64 = akar 4 x akar 16
= 2 x 4 = 8 selesai

Misalkan berapa akar dari 72
72 = 9 x 8 = 9 x 4 x 2
= 3 x 2 x akar 2, sama dengan 6 akar 2 atau

Sifat Akar-Akar Persamaan Kuadrat

Jika x₁ dan x₂ adalah akar-akar persamaan kuadrat ax² + bx + c = 0, maka:

x₁ + x₂ = –b/a

x₁.x₂ = c/a

|x₁ – x₂| = –D/a

(Mohon dingat! D = b² – 4.a.c)

Contoh Akar Kuadrat

√4 = 2
√9 = 3
√16 = 4
√25 = 5
√36 = 6
√49 = 7
√64 = 8
√81 = 9
√100 = 10
√169 = 13, karena 13 × 13 = 169
√1225 = 35, karena 35 × 35 = 1225

Akar dari 1

Akar dari 2

1.41421356237

Akar dari 3

1.7320508075688772935

Akar dari 4

Akar dari 5

2.2360679775

Akar dari 6

2.44948974278

Akar dari 7

2.64575131106

Akar dari 8

2.82842712475

Akar dari 9

Akar dari 10

3.16227766017

Akar dari 12

3.46410161514

Akar dari 13

3.60555127546

Akar dari 14

3.74165738677

Akar dari 24

4.89897948557

Akar dari 48

6.92820323028

√48 x √48=

Akar dari 49

Akar dari 69

8.30662386292

Akar dari 100

Akar dari 101

10.0498756211

Akar dari 123

11.0905365064

Akar dari 125

11.1803398875

Akar dari 484

Akar dari 625

Akar dari 1225

Akar dari 6000

77.4596669241

Akar dari 15000

122.474487139

√10 + √10

6.32455532034

√10 – √11

-0.15434713018

√10 – √11 / √5

cara menghitung √(10) – (√11 / √5)) = 1.67903796275

√10 – √11 x √5

cara menghitung √(10) – (√(11) x √(5)) = -4.25392082693

√10 + √11 – √5

cara menghitung √(10) + √(11) – √(5) = 4.24283447302

√10 + √11 / √5

cara menghitung √(10) + (√(11) / √(5)) = 4.64551735759

√10 + √11 x √5

cara menghitung √(10) + (√(11) x √(5)) = 10.5784761473

√10 x √11 + √5

cara menghitung (√(10) x √(11)) + √(5) = 12.7241564592

√10 x √11 – √5

cara menghitung (√(10) x √(11)) – √(5) = 8.2520205042

√10 x √11 – √5 + -√6

cara menghitung (√(10) x √(11)) – √(5) + (-√6)) = 5.80253076142

√10 / √11 / √5

cara menghitung (√(10) / √(11)) / √(5) = 0.42640143271

√10 / √11 – √5

cara menghitung (√(10) / √(11)) – √(5) = -1.28260538825

Cara Menyederhanakan Akar

Berikut ini adalah beberpa cara untuk menyederhanakan akar dengan cara:

Memfaktorkan

Tujuan menyederhanakan akar kuadrat adalah menuliskannya dalam bentuk yang mudah dipahami dan digunakan dalam soal matematika. Dengan memfaktorkan, angka yang besar akan dipecahkan menjadi dua atau lebih angka “faktor” yang lebih kecil, sebagai contohnya mengubah 9 menjadi 3 x 3. Setelah kita menemukan faktor ini, kita dapat menuliskan kembali akar kuadrat dalam bentuk yang lebih sederhana, terkadang bahkan mengubahnya menjadi bilangan bulat biasa. Sebagai contohnya, √9 = √(3×3) = 3. Ikuti langkah berikut ini untuk mempelajari proses ini dalam akar kuadrat yang lebih rumit.
Membagi

Bagi angka dengan bilangan prima terkecil yang mungkin. Jika angka yang berada di bawah tanda akar adalah bilangan genap, bagi dengan 2. Jika angkamu ganjil, maka cobalah bagi dengan 5. Jika tidak satupun dari pembagian ini memberikanmu hasil bilangan bulat, cobalah angka selanjutnya dalam daftar di bawah ini, membagi dengan setiap bilangan prima hingga mendapatkan bilangan bulat sebagai hasilnya. Anda hanya perlu menguji bilangan prima saja, karena semua angka lain memiliki bilangan prima sebagai faktornya. Sebagai contohnya, kamu tidak perlu menguji dengan angka 4, karena semua angka yang bisa dibagi 4 juga bisa dibagi 2, yang telah Anda coba sebelumnya: 2, 3, 5, 7, 11, 13, 17, dst.
Dikalikan
Tulis ulang akar kuadrat sebagai soal perkalian. Tetap tuliskan perkalian ini di bawah tanda akar, dan jangan lupa menyertakan kedua faktornya. Sebagai contoh, jika kamu mencoba menyederhanakan √98, Ikuti langkah di atas untuk menemukan bahwa 98 ÷ 2 = 49, jadi 98 = 2 x 49. Tulis ulang angka “98” dalam bentuk akar kuadrat aslinya menggunakan informasi ini: √98 = √(2 x 49).
Atau kalikan angka di dalam akar. Angka di dalam akar adalah angka yang berada di bawah tanda akar. Untuk mengalikan angka di dalam akar, kalikan angka-angka itu seperti mengalikan angka bulat. Pastikan untuk menuliskan hasil perkaliannya di bawah tanda akar. Contohnya: √15x√5, Anda dapat menghitung 15×5= 75. Jadi √15x√5=75

Contoh Penyederhanaan Akar

√75 = √25×3 = √25 x √3 = 5√3
Contoh soal, sederhanakan:
5√24 + 3√3(√18 + 2√32)
Pembahasan:
5√24 + 3√3(√18 + 2√32)
= 5√4 √6 + 3√3 √18 + 3√3 . 2√32
=5.2 √6 + 3√3 √9√2 + 3√3 .2√16√2
= 10√6 + 3√3 .3√2 + 3√3 . 2 .4√2
= 10√6 + 9√6 + 24√6 = 43√6
Hitung dan sederhanakan:
a) √2 + √4 + √8 + √16
b) √3 + √9 + √27
c) 2√2 + 2√8 + 2√32
Pembahasan
a) √2 + √4 + √8 + √16
= √2 + √4 + √4 √ 2 + √16 = √2 + 2 + 2√2 + 4 = 2 + 4 + √2 + 2√2 = 6 + 3√2
b) √3 + √9 + √27
= √3 + √9 + √9 √3 = √3 + 3 + 3√3 = 3 + 4√3
c) 2√2 + 2√8 + 2√32
= 2√2 + 2√4 √2 + 2√16 √2 = 2√2 + 2 (2)√2 + 2(4)√2 = 2√2 + 4√2 + 8√2 = 14√2

Menyelesaikan persamaan kuadrat dengan memfaktorkan

ax² + bx + c = 0 dapat dinyatakan menjadi a (x – x₁) (x – x₂) = 0.

Nilai x₁ dan x₂ disebut akar-akar (penyelesaian) persamaan kuadrat.

Bentuk simetri akar-akar persamaan kuadrat

Jumlah kuadrat akar-akar:
x₁² + x₂² = (x₁ + x₂)² – 2.x₁.x₂
Jumlah pangkat tiga akar-akar:
x₁³ + x₂³ = (x₁ + x₂)³ – 3.x₁.x₂.(x₁ + x₂)
Jumlah pangkat empat akar-akar:
x₁⁴ + x₂⁴ = (x₁² + x₂²)² – 2.x₁².x₂²

Hubungan Jenis Akar-akar PK dengan Nilai Diskriminan (D)

Jika D > 0 maka PK mempunyai 2 akar real yang berlainan

→ D = bilangan kuadrat berarti akar-akarnya rasional

→ D bukan bilangan kuadrat berarti akar-akarnya irasional

Jika D = 0 maka PK m,empunyai 1 akar real atau akar-akarnya kembar
Jika D ≥ 0 maka PK mempunyai 2 akar real/nyata
Jika D < 0 maka PK tidak mempuyai akar real / akar-akarnya imajiner
Jika kedua akar positif (x₁ > 0, x₂ > 0)

D ≥ 0

x₁ + x₂ > 0

x₁.x₂ > 0

Jika kedua akar negatif (x₁ < 0 dan x₂ < 0)

D ≥ 0

x₁ + x₂ < 0

x₁.x₂ > 0

Jika kedua akar berlainan tanda (1 positif, 1 negatif)

D > 0

x₁.x₂ < 0

Jika kedua akar bertanda sama (sama-sama positif/sama-sama negatif)

D ≥ 0

x₁.x₂ > 0

Jika kedua akar saling berlawanan (x₁ = –x₂)

D > 0

b = 0 (diperoleh dari x₁ + x₂ = 0)

x₁.x₂ < 0

Jika kedua akar saling berkebalikan (x₁ = 1/x₂)

D > 0

c = a

Contoh 1:
Tentukan nilai m agar x² + 4x + (m – 4) = 0 mempunyai 2 akar real
D ≥ 0
b² – 4ac ≥ 0
4² – 4.1.(m – 4) ≥ 0
16 – 4m + 16 ≥ 0
–4m ≥ –16 – 16
Semua dibagi –4
(Mohon dingat! Jika dibagi atau dikali bilangan negatif tanda pertidaksamaan dibalik)
m ≤ 4 + 4
m ≤ 8

Menyusun PK

PK dengan akar-akar x₁ dan x₂ adalah:

x² – (x₁ + x₂)x + (x₁.x₂) = 0

dengan kata lain:

x² – (jumlah akar-akar)x + (hasil kali akar-akar) = 0

Contoh 1:
Tentukan PK yang mempunyai akar-akar 2 dan –5:
x² – (2 + (–5))x + (2.(–5)) = 0
x² + 3x – 10 = 0

Contoh 2:
Jika x₁ dan x₂ adalah akar-akar PK: x² – 3x – 1 = 0, susun PK baru yang akar-akarnya 3x₁ + 2 dan 3x₂ + 2!
Karena PK tersebut tidak dapat difaktorkan,
x₁ + x₂ = –b/a = –(– 3) /1 = 3
x₁.x₂ = c/a = –1/1 = –1
Misal akar-akar PK baru adalah y₁ dan y₂:
y₁ + y₂ = 3.x₁ + 2 + 3.x₂ + 2
= 3(x₁ + x₂) + 4 = 9 + 4 = 13
y₁.y₂ = (3x₁ + 2).(3x₂ + 2)
= 9.x₁.x₂ + 6.x₁ + 6.x₂ + 4
= 9.(–1) + 6.3 + 4 = –9 + 18 + 4 = 13
Jadi PK barunya:
x² – (y₁ + y₂)x + (y₁.y₂) = 0
x² – 13x + 13 = 0

Soal

Tentukan nilai k agar persamaan² kuadrat berikut memiliki akar kembar

a. x²-2x+k=0
b. 2x²-4x+k=0
c. kx²-6x+1/2=0
d. 3x²-kx+5=0
e. 2kx²+3x+2=0

Jawaban

suatu persamaan kuadrat akan memiliki akar kembar jika D = 0
D = b² – 4ac

1.] x² – 2x + k = 0
D = 0
4 – 4 . 1 . k = 0
4 – 4k = 0
4k = 4
k = 1

2.] 2x² – 4x + k = 0
D = 0
16 – 4 . 2 . k = 0
16 – 8k = 0
8k = 16
k = 2

3.] kx² – 6x + 1/2 = 0
36 – 4 . k . 1/2 = 0
36 – 2k = 0
2k = 36
k = 18

4.] 3x² – kx + 5 = 0
D = 0
k² – 4 . 3 . 5 = 0
k² – 60 = 0
k = ± √60

5.] 2kx² + 3x + 2 = 0
D = 0
9 – 4 . 2k . 2 = 0
9 – 16k = 0
16k = 9
k = 9/16

Fungsi Akar Kuadrat

Fungsi akar kuadrat utama $\scriptstyle f(x)={\sqrt {x}}$ (biasanya hanya disebut sebagai “fungsi akar kuadrat”) adalah fungsi yang memetakan himpunan bilangan real taknegatif R⁺ ∪ {0} kepada himpunan itu sendiri, dan, seperti semua fungsi, selalu memiliki nilai balikan yang tunggal. Fungsi akar kuadrat juga memetakan bilangan rasional ke dalam bilangan aljabar (adihimpunan bilangan rasional); $\scriptstyle {\sqrt {x}}$ adalah rasional jika dan hanya jika x adalah bilangan rasional yang dapat dinyatakan sebagai hasil bagi dari dua kuadrat sempurna. Di dalam istilah geometri, fungsi akar kuadrat memetakan luas dari persegi kepada panjang sisinya.

Untuk setiap bilangan real x

{\sqrt {x^{2}}}=\left|x\right|={\begin{cases}x,&{\mbox{if }}x\geq 0\\-x,&{\mbox{if }}x<0.\end{cases}}

(lihat nilai absolut)

Untuk setiap bilangan real taknegatif x dan y,

{\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}

dan

{\sqrt {x}}=x^{1/2}.

Fungsi akar kuadrat adalah kontinu untuk setiap bilangan taknegatif x dan terdiferensialkan untuk setiap bilangan positif x. Turunannya diberikan oleh

f'(x)={\frac {1}{2{\sqrt {x}}}}.

Deret Taylor dari √1 + x di dekat x = 0 konvergen ke | x | < 1 dan diberikan oleh

{\sqrt {1+x}}=1+\textstyle {\frac {1}{2}}x-{\frac {1}{8}}x^{2}+{\frac {1}{16}}x^{3}-{\frac {5}{128}}x^{4}+\dots \!

Bilangan Rasional adalah

Bilangan yang dapat dinyatakan dalam bentuk ^a/_b dengan a, b bilangan bulat dan b ≠ 0. Bilangan rasional merupakan gabungan dari bilangan bulat, nol, dan pecahan. Contoh bilangan rasional adalah -5, ^-1/₂, 0, 3, ³/₄, dan ⁵/_9.

Bilangan Irasional adalah

Bilangan yang tidak dapat dinyatakan dalam bentuk ^a/_b dengan a, b bilangan bulat dan b ≠ 0.
Bilangan-bilangan tersebut, jika dihitung dengan kalkulator merupakan desimal yang tak berhenti atau bukan desimal yang berulang. Misalnya
√2 = 1,414213562 …. Selanjutnya, gabungan antara bilangan rasional dan irasional disebut bilangan real.

Soal dan Jawaban Lainnya Dari Akar Kuadrat / Pangkat

1. Soal: Hasil dari 8 ² + 4² – 5² adalah…

Jawaban:

8² + 4²- 5² = 64 + 16 – 25 = 55

2. Soal: Hasil dari √123√123 x 123 adalah…

Jawaban:

√123√123²
123 x 123
15129 atau 1,5129 x 10⁴

3. Soal: Sederhanakan 5√24 + 3√3(√18 + 2√32)

Jawaban:

5√24 + 3√3(√18 + 2√32)
= 5√4 √6 + 3√3 √18 + 3√3 . 2√32
=5.2 √6 + 3√3 √9√2 + 3√3 .2√16√2
= 10√6 + 3√3 .3√2 + 3√3 . 2 .4√2
= 10√6 + 9√6 + 24√6 = 43√6

4. Soal: Kamar tidur Tina berbentuk kubus. Lantai kamar tidur Tina tertutup ubin berukuran 30 cm x 30 cm sebanyak 81 buah. Berapa panjang sisi kamar Doni?

Jawaban:

Luas lantai kamar = 30 cm x 30 cm × 81 = 72.900 cm².
Panjang sisi kamar = √72.900 = 270 cm
Jadi, panjang sisi kamar Roni adalah 270 cm.

5. Dengan menggunakan pola yang diberikan, cari nomor yang hilang:

1² + 2² + 2² = 3²2² + 3² + 6² = 7²3² + 4² + 12² = 13²4² + 5² + _² = 21²5² + _² + 30² = 31²6² + 7² + _² ₌ _²

Jawaban:

1² + 2² + 2² = 3²2² + 3² + 6² = 7²3² + 4² + 12² = 13²4² + 5² + 20² = 21²5² + 6² + 30² = 31²6² + 7² + 42² = 43²

6. Soal: Hasil dari √( x + 1) = 4 adalah…

Jawaban:

[ √( x + 1) ] 2 = 4 ^{2

x + 1 = 16

x = 15}

CATATAN: Karena kita mengkuadratkan kedua sisi, tanpa menempatkan kondisi apa pun, solusi tambahan mungkin dapat diperkenalkan, lihat juga solusi lainnya.

Sisi kiri (kiri) dari persamaan yang diberikan ketika x = 15
Kiri = √ (x + 1) = √ (15 + 1) = 4
Sisi Kanan (kanan) dari persamaan yang diberikan ketika x = 15
Kanan= 4.

7. Soal: Hasil dari √( 3 x + 1) = x – 3 adalah…

Jawaban:

[ √( 3 x + 1) ]² = (x – 3) ^{2

3 x + 1 = x 2 – 6 x + 9

x 2 – 9 x + 8 = 0

x = 8 and x = 1}

CATATAN: Karena kita mengkuadratkan kedua sisi, solusi lainnya dapat diperkenalkan, memeriksa solusi dalam persamaan asli diperlukan.
1. periksa persamaan untuk x = 8.
Sisi kiri (kiri) dari persamaan yang diberikan ketika x = 8
Kiri = √ (3 x + 1) = √ (3 * 8 + 1) = 5
Sisi Kanan (Kanan) dari persamaan yang diberikan ketika x = 8
Kanan = x – 3 = 8 – 3 = 5
2. periksa persamaan untuk x = 1.
Kiri = √ (3 x + 1) = √ (3 * 1 + 1) = 2
Sisi Kanan (Kanan) dari persamaan yang diberikan ketika x = 8
Kanan= x – 3 = 1 – 3 = -2
Untuk x = 8 sisi kiri dan kanan persamaan adalah sama dan x = 8 adalah solusi untuk persamaan yang diberikan. x = 1 bukanlah solusi untuk persamaan yang diberikan; itu adalah solusi lain yang dapat diperkenalkan karena peningkatan kuadrat 2.

8. Soal: Hasil dari ³√( x² + 2 x + 8 ) = 2 adalah…

Jawaban:

[ ³√( x² + 2 x + 8 ) ]³ = 2 ³x² + 2 x + 8 = 8
x² + 2 x = 0
x (x + 2) = 0
x = 0 dan x = – 2.

Mari kita periksa solusi yang didapat sebagai latihan.
1. x = 0
Sisi kiri (Kiri) dari persamaan yang diberikan ketika x = 0
Kiri = 3√ (x 2 + 2 x + 8) = cube_root (0 + 0 + 8) = 2
Sisi Kanan (Kanan) dari persamaan yang diberikan ketika x = 0
Kanan = 2
2. x = -2
Sisi kiri (Kiri) dari persamaan yang diberikan ketika x = 0
Kiri = 3√ (x 2 + 2 x + 8)
= 3√ ((-2) 2 + 2 * (- 2) + 8) = cube_root (8) = 2
Sisi Kanan (Kanan) dari persamaan yang diberikan ketika x = 0
Kanan = 2

9. Soal: Luas dua buah persegi adalah 441 cm² dan 625 cm².
Hitunglah panjang sisi kedua persegi itu!

Jawaban:

Panjang sisi persegi =√441 = 21 cm, √625 = 25 cm Jadi, panjang kedua sisi persegi tersebut adalah 21 cm dan 25 cm.

10. Soal: Nilai dari $\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}-3$ adalah…

Jawaban:

Untuk memudahkan perhitungan, misalkan $\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} = p$

$\displaystyle \begin{aligned} p &=\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}} ~~~ ... \:\text{(kedua ruas pangkat 3)}\\ p^3 &=\left(2+\sqrt{5}\right)+\left(2-\sqrt{5}\right)+3\left( \sqrt[3]{2+\sqrt{5}}\cdot\sqrt[3]{2-\sqrt{5}}\right)\left( \sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}\right) \\ p^3 & = 4 + 3\cdot \sqrt[3]{-1}\cdot p \\ 0 &= p^3 +3p -4 \\ 0 &= (p-1)(p^2+p+4) \end{aligned}$

Karena faktor $(p^2+p+4)$ definit positif (selalu positif), maka $(p-1) = 0 \rightarrow p = 1$ , sehingga $\sqrt[3]{2+\sqrt{5}}+\sqrt[3]{2-\sqrt{5}}-3 = p - 3 = 1 - 3 = -2$

Jawaban : A

catatan:
$\boxed{~(a+b)^3 = a^3 + b^3 + 3ab(a+b)~}$

11. Soal: Hitung dan sederhanakan bentuk akar berikut ini:
a) √2 + 3√2 + 5√2
b) 5√3 + 3√3 − √3
c) 8√3 + 6 √2 + 12√3 − 4√2

Jawaban:
a) √2 + 3√2 + 5√2
= (1 + 3 + 5)√2 = 9√2

b) 5√3 + 3√3 − √3
= (5 + 3 − 1)√3 = 7√3

c) 8√3 + 6 √2 + 12√3 − 4√2
= 8√3 + 12√3 + 6√2 − 4√2 = (8 + 12)√3 + (4 − 2)√2 = 20√3 + 2√2

12. Soal: Sederhanakan bentuk berikut:
a) 5/√3
b) 20/√5

Jawaban:

a) 5/√3
5 √3 5
= ^_____ x ^___ = ^___ √3
√3 √3 3

b) 20/√5

      20     √5      20
= ^_____ x ^___ = ^_____ √5  = 4 √5
     √5     √5       5

13. Soal: Hasil dari 4² x 32^3/5 x 128^-3/7 adalah…

A.   2³
B.   2⁴
C.   2⁵
D.   2⁶
E.   2⁷

Jawaban:

4² x 32^3/5 x 128^-3/7= (2²)² x (2⁵)^3/5 x (2⁷)^-3/7Jawaban B. 24.

14. Soal: Jika a = 27 dan b = 32, maka nilai dari 3(a^-1/3) x 4b^2/5 adalah…

a.   -25
b.   -16
c.   0
d.   16
e.   25

Jawaban:

a = 27 dan b = 32 maka:
3(a^1/3) x 4b^2/5
= 3(27^-1/3)x4(32^2/5)
= 3(3^3(-1/3)) x 4 (2^5(2/5))
= 3(3^-1) x 4(2²)
= 3⁰ x 4(4)
= 1 x 16
= 16

Jawaban: D. 16.

15. Soal: Bentuk sederhana dari (1 + 3√2) − (4 − √50) adalah…

A. −2√2 − 3
B. −2√2 + 5
C. 8√2 − 3
D. 8√2 + 3
E. 8√2 + 5

Jawaban:

Hilangkan tanda kurungnya terlebih dulu, jika ada tanda minus di depan kurung, kalikan masuk, jadinya seperti berikut:

(1 + 3√2) − (4 − √50)
= 1 + 3√2 − 4 + √50

√50 sama saja dengan √25 × √ 2 jadi sama dengan 5√2, tinggal disederhanakan:

= 1 + 3√2 −4 + 5√2
= 1 − 4 + 3√2 + 5√2
= −3 + 8√2
= 8√2 −3

16. Soal: Nilai x yang memenuhi, jika 5^4+x = 3. 125 adalah…

A.   2
B.   4
C.   3
D.   5
E.   1

Jawaban:
5^{4 + x} = 3.125

5^{4 + x} = 5⁶

4 + x = 5

x = 1

Jawab: E. 1.

17. Soal: Selesaikan: 3x2 + 5x − 2 = 0

Jawaban:

3x2 + 5x − 2 = 0
(3x − 1)(x + 2) = 0
3x − 1 = 0 or x + 2 = 0
Jadi, x = 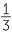or x = −2

18. Soal: Sederhanakan: −

Jawaban:

−	= −
	= −
	=
	=
	=

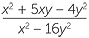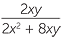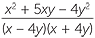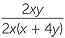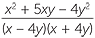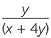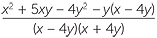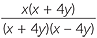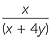19. Soal: Temukan semua solusi bilangan bulat positif: ab + 2a + 5b = 38

Jawaban:

Faktor kedua faktor pertamanya sebagai (b + 2). Kami menambahkan 10 ke kedua sisi, sehingga kita dapat faktor berpasangan. Demikianlah,

ab + 2a + 5b= 38
ab + 2a + 5b + 10= 48
a(b + 2) + 5(b + 2)= 48
(a + 5)(b + 2)= 48

Menyamakan setiap golongan dengan faktorisasi dan kofaktor 48 dan pemecahannya, kami menemukan bahwa satu-satunya solusi bilangan bulat positif adalah a = 11, b = 1; a = 1, b = 6; a = 3, b = 4; a = 7, b = 2

20. Soal: Sederhanakan:
a b × c ÷

Jawaban & Pembahasan

a			=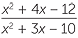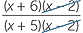
			=

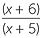b	×	= ×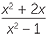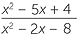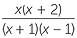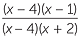
		=
		=

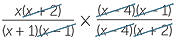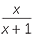c	Balikkan dan kalikan sebelum di-faktorisasi.
	÷	= ×
		= ×
		=

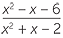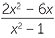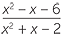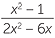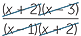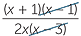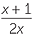21. Berapa akar kuadrat dari 124?

penyelesaiannya adalah kita cari 2 jawaban terdekat dari akar kuadrat 124, maka akan kita temukan hasil sementara 11 dan 12
11^2 = 121 —-> kurang dari 124 / lebih kecil
12^2 = 144 —-> terlalu besar
kesimpulan sementara jawaban nya adalah 11 koma
kemudian kita cari selisih antara 124 dan 121 ——> 124-121 = 3
kemudian kita cari selisih kedua nilai terdekat 144 dan 121 ——> 144-121 = 23
jadi kita peroleh pecahannya adalah 3/23
sehingga di dapatkan jawaban akar dari 124 adalah 11 + 3/23 = 11,13

22. Selesaikan x³ – 7x² + 4x + 12 = 0

Jawaban:

f(x) = x³ – 7x² + 4x + 12

Nilai yang mungkin adalah ±1, ±2, ±3, ±4, ±6, ±12

Kita mendapatkan f(–1) = –1 – 7 – 4 + 12 = 0

Jadi, (x + 1) adalah faktor dari f(x)

x³ – 7x² + 4x + 12
= (x + 1)(x² – 8x + 12)
= (x + 1)(x – 2)(x – 6)

Jadi, akarnya –1, 2, 6

23. Temukan akar f(x) = 2x³ + 3x² – 11x – 6 = 0, mengingat bahwa itu memiliki setidaknya satu akar bilangan bulat.

Jawaban:

Karena konstanta dalam persamaan yang diberikan adalah 6, kita tahu bahwa akar bilangan bulat harus menjadi faktor 6. Nilai yang mungkin adalah ±1, ±2, ±3, ±6

Langkah 1: Gunakan teorema faktor untuk menguji nilai yang mungkin dengan trial and error.

f(1) = 2 + 3 – 11 – 6 ≠ 0
f(–1) = –2 + 3 + 11 – 6 ≠ 0
f(2) = 16 + 12 – 22 – 6 = 0
Kami menemukan bahwa akar pangkat 2.

Langkah 2: Temukan akar lainnya dengan inspeksi atau dengan pembagian sintetis.

2x³ + 3x² – 11x – 6
= (x – 2)(ax² + bx + c)
= (x – 2)(2x² + bx + 3)
= (x – 2)(2x² + 7x + 3)
= (x – 2)(2x + 1)(x +3)

Jadi, akarnya x= 2, – ½, – 3

24. Jika diketahui $x$ dan $y$ adalah bilangan riil dengan $x >1$ dan $y > 0$ . Jika $xy=x^y$ dan $\dfrac{x}{y} = x^{5y}$ , maka $x^2+3y = ...$

Jawaban:

Kalikan kedua persamaan

$\displaystyle \begin{aligned} (xy)\left(\frac{x}{y}\right)&=(x^y)(x^{5y})\\ x^2 &= x^{6y}\\ \therefore\:y&=\frac{1}{3} \end{aligned}$

Subtitusikan nilai $y$ ke pers. pertama:

$\displaystyle \begin{aligned} x\left(\frac{1}{3}\right)&=x^\frac{1}{3} &~~~~~\text{(pangkat tiga kedua ruas)} \\ \frac{x^3}{27}&=x &~~~~~~\text{(nilai }x > 0)\\ \therefore\: x^2 &= 27 \end{aligned}$

Jadi $x^2 + 3y = 27 + 3(\frac{1}{3})=28$

Jawaban : B

catatan :

Sifat eksponen:

$\boxed{a^m+a^n=a^{m+n}}$

$\boxed{(a^m)^n=a^{mn}}$

25. Selesaikan x² – 4 x + 3 = 0

Jawaban:
x² – 4 x + 3 = 0
(x – 3) (x – 1) = 0
x – 3 = 0 atau x – 1 = 0
x = 3 atau x = 1

Jadi, penyelesaian dari x² – 4 x + 3 = 0 adalah 3 dan 1.

26. Tentukan himpunan penyelesaian dari (x – 2)² = x – 2.

Jawaban:

(x – 2)² = x – 2
x² – 4 x + 4 =  x – 2
x² – 5 x + 6 = 0
(x – 3) (x – 2) = 0
x – 3 = 0   atau   x – 2 = 0
x = 3   atau          x = 2

Jadi, himpunan penyelesaiannya adalah {3 , 2}.

27. Tentukan penyelesaian dari 2 x² + 7 x + 6 = 0

Jawaban:

2 x² + 7 x + 6 = 0
2 x² + 4 x + 3 x + 6 = 0
2 x (x + 2) + 3 (x + 2) = 0
(x + 2) (2 x + 3) = 0
x +2 = 0 atau 2 x + 3 = 0
x = –2 atau x = – 1

Jadi, penyelesaiannya adalah –2 dan –1

28. Tentukan himpunan penyelesaian dari x² – 6 x + 5 = 0.

Penjelasan:

Menyelesaikan persamaan kuadrat dengan melengkapkan kuadrat sempurna

Persamaan kuadrat ax² + bx + c = 0 dapat diselesaikan dengan mengubahnya menjadi (x + p)² = q.

Jawaban:

x² – 6 x + 5 = 0
x² – 6 x + 9 – 4 = 0
x² – 6 x + 9 = 4
(x – 3)² = 4
x – 3 = 2 atau x – 3 = –2
x = 5 atau x = 1

Jadi, himpunan penyelesaiannya adalah{ 1 , 5}.

29. Tentukan penyelesaian dari 2 x² – 8 x + 7 = 0.

Jawaban:

2 x² – 8 x + 7 = 0
2 x² – 8 x + 8 – 1 = 0
2 x² – 8 x + 8 = 1
2 (x² – 4 x + 4) = 1
2 (x – 2)² = 1
(x – 2)² = ½

x – 2 = $\sqrt{\frac{1}{2}}$ atau x – 2 = – $\sqrt{\frac{1}{2}}$

x = 2 + $\frac{1}{2} \sqrt{2}$ atau x = 2 – $\frac{1}{2} \sqrt{2}$

Jadi, penyelesaiannya adalah 2 + $\frac{1}{2} \sqrt{2}$ dan 2 – $\frac{1}{2} \sqrt{2}$

30. Tentukan himpunan penyelesaian dari x² + 7x – 30 = 0.

Penjelasan:

Menyelesaikan persamaan kuadrat dengan menggunakan rumus

Rumus penyelesaian persamaan kuadrat a x² + b x + c = 0 adalah

$x_{1,2}=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$

Jawab:

x² + 7x – 30 = 0

a = 1 , b = 7 , c = – 30

$x_{1,2}=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$

$x_{1,2}=\frac{-7\pm\sqrt{7^{2}-4.1.(-30)}}{2.1}$

$x_{1,2}=\frac{-7\pm\sqrt{49+120}}{2}$

$x_{1,2}=\frac{-7\pm\sqrt{169}}{2}$

$x_{1,2}=\frac{-7\pm 13}{2}$

x = 3 atau x = –10

Jadi, himpunan penyelesaiannya adalah {–10 , 3}.

31. Soal: Hasil √10 x √11 – √5 + -√6 x (√10 x √11 – √5 + -√6) adalah…

Jawaban:

Cara mengerjakan: (√(10) x √(11)) – √(5) + ((-√6)) x ((√(10) x √(11)) – √(5) + (-√6)))) =

5.802530761425.80253076142

32. Soal: Hasil √10 / √11 / √5 + √6 / √10 / √11 / √5 adalah…

Jawaban:

Cara mengerjakan: ((√(10) / √(11) / √(5)) + (((√(6) / √(10)) / √(11)) / √(5)) =

0.53084802628

33. Soal: √10 + √11 + √5 + √6 x √10 x √11 x √5 adalah

Jawaban:

Cara mengerjakan: √(10) + √(11) + √(5) + √(6) x √(10) x √(11) x √(5)) =

66.1605968934

34. Soal: √10 + √11 + √5 + √6 – √10 – √11 – √5 adalah

Cara mengerjakan: √(10) + √(11) + √(5) + √(6) – √(10) – √(11) – √(5) =

2.44948974278

35. Soal: √10 x √11 x √5 x √6 / √10 / √11 / √5 adalah

Cara mengerjakan: (((√(10) x √(11) x √(5) x √(6)) / √(10)) / √(11)) / √(5) =

2.44948974278

Bacaan Lainnya

Sumber bacaan: Math is Fun, Australian Mathematical Sciences Institute, Varsity Tutors

Akar Kuadrat / Pangkat, Penjelasan dan Contoh

Akar Kuadrat Adalah

Cara Menghitung Akar Kuadrat Dengan Faktorisasi

Sifat Akar-Akar Persamaan Kuadrat

Contoh Akar Kuadrat

Akar dari 1

Akar dari 2

Akar dari 3

Akar dari 4

Akar dari 5

Akar dari 6

Akar dari 7

Akar dari 8

Akar dari 9

Akar dari 10

Akar dari 12

Akar dari 13

Akar dari 14

Akar dari 24

Akar dari 48

√48 x √48=

Akar dari 49

Akar dari 69

Akar dari 100

Akar dari 101

Akar dari 123

Akar dari 125

Akar dari 484

Akar dari 625

Akar dari 1225

Akar dari 6000

Akar dari 15000

√10 + √10

√10 – √11

√10 – √11 / √5

√10 – √11 x √5

√10 + √11 – √5

√10 + √11 / √5

√10 + √11 x √5

√10 x √11 + √5

√10 x √11 – √5

√10 x √11 – √5 + -√6

√10 / √11 / √5

√10 / √11 – √5

Cara Menyederhanakan Akar

Memfaktorkan

Membagi

Dikalikan

Contoh Penyederhanaan Akar

Menyelesaikan persamaan kuadrat dengan memfaktorkan

Bentuk simetri akar-akar persamaan kuadrat

Hubungan Jenis Akar-akar PK dengan Nilai Diskriminan (D)

Menyusun PK

Soal

Tentukan nilai k agar persamaan² kuadrat berikut memiliki akar kembar

Jawaban

Fungsi Akar Kuadrat

Bilangan Rasional adalah

Bilangan Irasional adalah

Soal dan Jawaban Lainnya Dari Akar Kuadrat / Pangkat

1. Soal: Hasil dari 8 ² + 4² – 5² adalah…

2. Soal: Hasil dari √123√123 x 123 adalah…

3. Soal: Sederhanakan 5√24 + 3√3(√18 + 2√32)

4. Soal: Kamar tidur Tina berbentuk kubus. Lantai kamar tidur Tina tertutup ubin berukuran 30 cm x 30 cm sebanyak 81 buah. Berapa panjang sisi kamar Doni?

5. Dengan menggunakan pola yang diberikan, cari nomor yang hilang:

12 + 22 + 22 = 32 22 + 32 + 62 = 72 32 + 42 + 122 = 132 42 + 52 + _2 = 212 52 + _2 + 302 = 312 62 + 72 + _2 = _2

6. Soal: Hasil dari √( x + 1) = 4 adalah…

7. Soal: Hasil dari √( 3 x + 1) = x – 3 adalah…

8. Soal: Hasil dari 3√( x 2 + 2 x + 8 ) = 2 adalah…

9. Soal: Luas dua buah persegi adalah 441 cm² dan 625 cm². Hitunglah panjang sisi kedua persegi itu!

11. Soal: Hitung dan sederhanakan bentuk akar berikut ini: a) √2 + 3√2 + 5√2 b) 5√3 + 3√3 − √3 c) 8√3 + 6 √2 + 12√3 − 4√2

12. Soal: Sederhanakan bentuk berikut: a) 5/√3 b) 20/√5

13. Soal: Hasil dari 42 x 323/5 x 128-3/7 adalah…

14. Soal: Jika a = 27 dan b = 32, maka nilai dari 3(a-1/3) x 4b2/5 adalah…

15. Soal: Bentuk sederhana dari (1 + 3√2) − (4 − √50) adalah…

16. Soal: Nilai x yang memenuhi, jika 54+x = 3. 125 adalah…

A. 2 B. 4 C. 3 D. 5 E. 1

17. Soal: Selesaikan: 3x2 + 5x − 2 = 0

18. Soal: Sederhanakan: <img decoding="async" class="blue-box" src="http://amsi.org.au/teacher_modules/F0/F0t13.png" alt="F0t13.pdf" /> − <img decoding="async" class="blue-box" src="http://amsi.org.au/teacher_modules/F0/F0t14.png" />

19. Soal: Temukan semua solusi bilangan bulat positif: ab + 2a + 5b = 38

1² + 2² + 2² = 3²2² + 3² + 6² = 7²3² + 4² + 12² = 13²4² + 5² + _² = 21²5² + _² + 30² = 31²6² + 7² + _² ₌ _²

8. Soal: Hasil dari ³√( x² + 2 x + 8 ) = 2 adalah…

9. Soal: Luas dua buah persegi adalah 441 cm² dan 625 cm².
Hitunglah panjang sisi kedua persegi itu!

11. Soal: Hitung dan sederhanakan bentuk akar berikut ini:
a) √2 + 3√2 + 5√2
b) 5√3 + 3√3 − √3
c) 8√3 + 6 √2 + 12√3 − 4√2

12. Soal: Sederhanakan bentuk berikut:
a) 5/√3
b) 20/√5

13. Soal: Hasil dari 4² x 32^3/5 x 128^-3/7 adalah…

14. Soal: Jika a = 27 dan b = 32, maka nilai dari 3(a^-1/3) x 4b^2/5 adalah…

16. Soal: Nilai x yang memenuhi, jika 5^4+x = 3. 125 adalah…

A. 2
B. 4
C. 3
D. 5
E. 1

18. Soal: Sederhanakan: −

22. Selesaikan x³ – 7x² + 4x + 12 = 0

23. Temukan akar f(x) = 2x³ + 3x² – 11x – 6 = 0, mengingat bahwa itu memiliki setidaknya satu akar bilangan bulat.

25. Selesaikan x² – 4 x + 3 = 0

26. Tentukan himpunan penyelesaian dari (x – 2)² = x – 2.

27. Tentukan penyelesaian dari 2 x² + 7 x + 6 = 0

28. Tentukan himpunan penyelesaian dari x² – 6 x + 5 = 0.

29. Tentukan penyelesaian dari 2 x² – 8 x + 7 = 0.

30. Tentukan himpunan penyelesaian dari x² + 7x – 30 = 0.