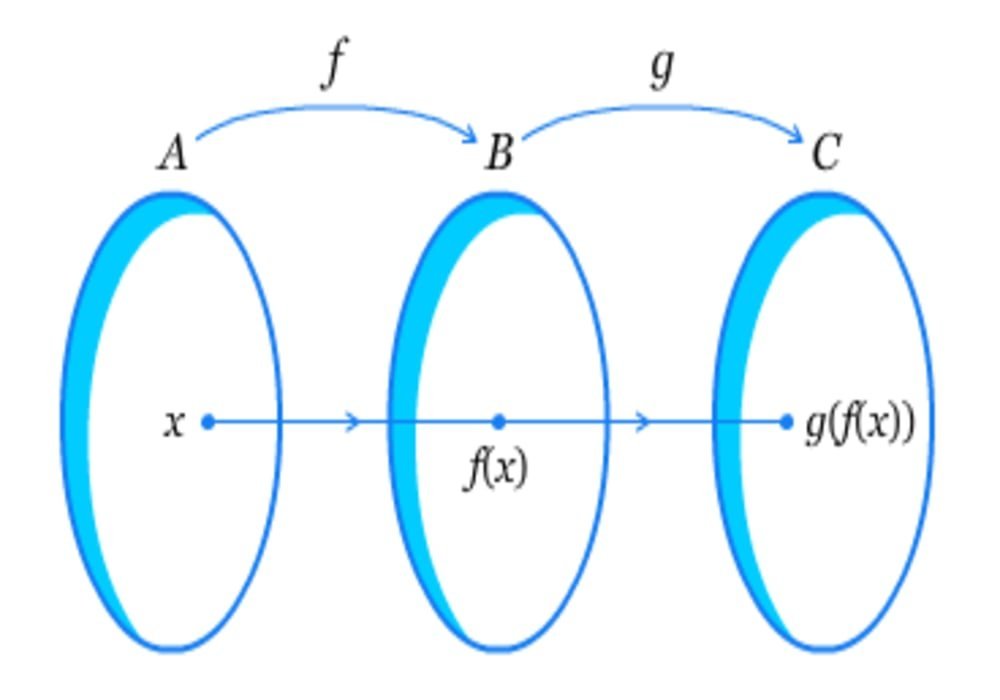
Fungsi Invers Kebalikan dalam Matematika
Fungsi Invers (atau fungsi invers kebalikan) adalah (dalam matematika) fungsi yang merupakan kebalikan aksi dari suatu fungsi.
Contohnya anggap saja 
Bila dapat ditentukan sebuah fungsi 





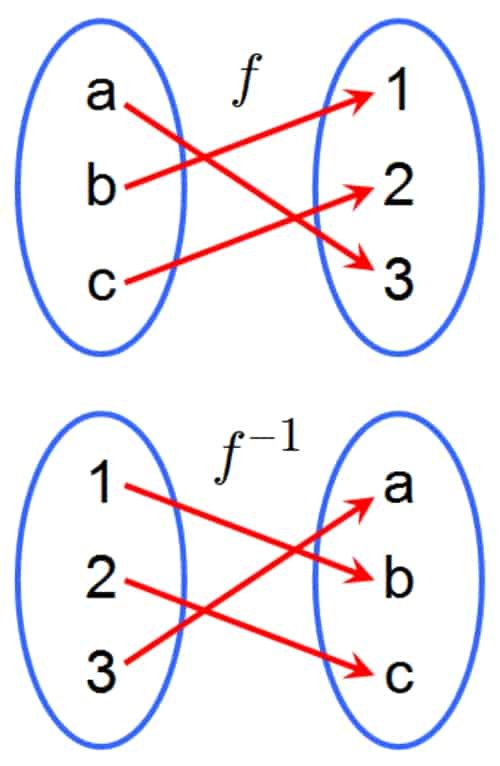
Sebelum mengetahui fungsi ini maka harus mengenali dahulu fungsi yang memiliki invers.
Fungsi 

Jika fungsi 


Kemudian ketika suatu bilangan itu dioperasikan dengan inversnya, maka akan menghasilkan identitas.
Identitas adalah suatu bilangan yang jika dioperasikan dengan suatu bilangan, maka akan menghasilkan suatu bilangan tersebut dan pada operasi perkalian, identitasnya adalah 1 karena apabila dikalikan dengan suatu bilangan hasilnya suatu bilangan.
Sedangkan, pada penjumlahan identitasnya adalah 0 karena bila dijumlahkan dengan bilangan tertentu hasilnya bilangan tertentu.
Pada fungsi juga berlaku demikian, sebuah fungsi bila dikomposisikan dengan invers maka menghasilkan fungsi identitas, yaitu 
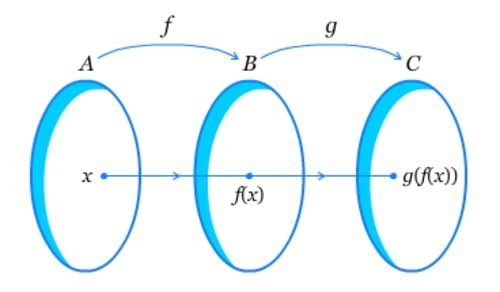
Contoh Fungsi Invers Kebalikan
- Tentukan
!
- Tentukan
!
- Tentukan
!
- Tentukan
!
(karena
)
- Tentukan
!
- Tentukan
!
Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar
- Fungsi Matematika: Linear, Konstan, Identitas – Beserta Soal dan Jawaban
- Topologi Matematika – Contoh Soal dan Jawaban Ruang Topologi
- Rumus Matematika Keuangan – Contoh Soal dan Jawaban
- Induksi Matematika Rumus, Pembuktian, Deret, Keterbagian, Pertidaksamaan, Soal, Pembahasan dan Jawaban
- Jenis dan Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
- Berapa Kecerdasan IQ Anda? Tes IQ Anda Disini
- Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
- Tulisan Menunjukkan Kepribadian Anda & Bagaimana Cara Anda Menulis?
- Penyakit yang dapat dicegah dengan vaksin – Wajib diketahui
- Top 10 Sungai Terpanjang Di Dunia
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya