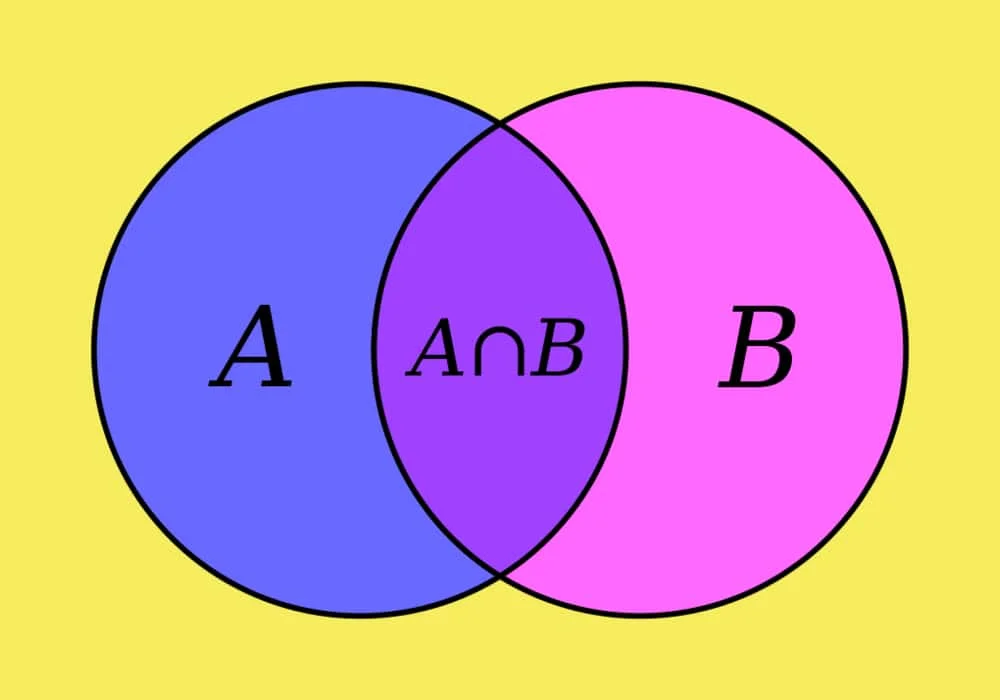
Rumus Himpunan Matematika
Hukum komutatif
- p ∩ q ≡ q ∩ p
- p ∪ q ≡ q ∪ p
Hukum asosiatif
- (p ∩ q) ∩ r ≡ p ∩ (q ∩ r)
- (p ∪ q) ∪ r ≡ p ∪ (q ∪ r)
Hukum distributif
- p ∩ (q ∪ r) ≡ (p ∩ q) ∪ (p ∩ r)
- p ∪ (q ∩ r) ≡ (p ∪ q) ∩ (p ∪ r)
Hukum identitas
- p ∩ S ≡ p
- p ∪ ∅ ≡ p
Hukum ikatan
- p ∩ ∅ ≡ ∅
- p ∪ S ≡ S
Hukum negasi
- p ∩ p’ ≡ ∅
- p ∪ p’ ≡ S
Hukum negasi ganda
- (p’)’ ≡ p
Hukum idempotent
- p ∩ p ≡ p
- p ∪ p ≡ p
Hukum De Morgan
- (p ∩ q)’ ≡ p’ ∪ q’
- (p ∪ q)’ ≡ p’ ∩ q’
Hukum penyerapan
- p ∩ (p ∪ q) ≡ p
- p ∪ (p ∩ q) ≡ p
Negasi S dan ∅
- S’ ≡ ∅
- ∅’ ≡ S
Himpunan Matematika

Teori himpunan, yang baru diciptakan pada akhir abad ke-19, sekarang merupakan bagian yang tersebar dalam pendidikan matematika yang mulai diperkenalkan bahkan sejak tingkat sekolah dasar. Teori ini merupakan bahasa untuk menjelaskan matematika modern. Teori himpunan dapat dianggap sebagai dasar yang membangun hampir semua aspek dari matematika dan merupakan sumber dari mana semua matematika diturunkan.
Operasi Dasar Himpunan Matematika
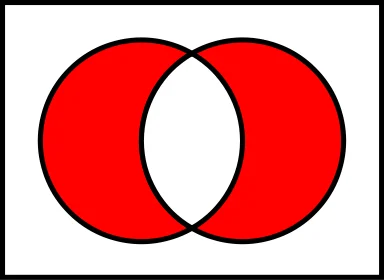
Gabungan

Dua himpunan atau lebih yang digabungkan bersama-sama. Operasi gabungan A ∪ B setara dengan A atau B, dan anggota himpunannya adalah semua anggota yang termasuk himpunan A ataupun B.
Contoh:
- {1, 2} ∪ {1, 2} = {1, 2}.
- {1, 2} ∪ {2, 3} = {1, 2, 3}.
- {Budi} ∪ {Dani} = {Budi, Dani}.
Beberapa sifat dasar gabungan:
- A ∪ B = B ∪ A.
- A ∪ (B ∪ C) = (A ∪ B) ∪ C.
- A ⊆ (A ∪ B).
- A ∪ A = A.
- A ∪ ∅ = A.
- A ⊆ Bjika dan hanya jikaA ∪ B = B.
Irisan
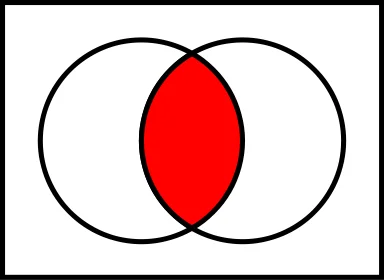
Operasi irisan A ∩ B setara dengan AdanB. Irisan merupakan himpunan baru yang anggotanya terdiri dari anggota yang dimiliki bersama antara dua atau lebih himpunan yang terhubung. Jika A ∩ B = ∅, maka A dan B dapat dikatakan disjoint (terpisah).
Contoh:
- {1, 2} ∩ {1, 2} = {1, 2}.
- {1, 2} ∩ {2, 3} = {2}.
- {Budi, Cici} ∩ {Dani, Cici} = {Cici}.
- {Budi} ∩ {Dani} = ∅.
Beberapa sifat dasar irisan:
- A ∩ B = B ∩ A.
- A ∩ (B ∩ C) = (A ∩ B) ∩ C.
- A ∩ B ⊆ A.
- A ∩ A = A.
- A ∩ ∅ = ∅.
- A ⊂ B jika dan hanya jika A ∩ B = A.
Komplemen
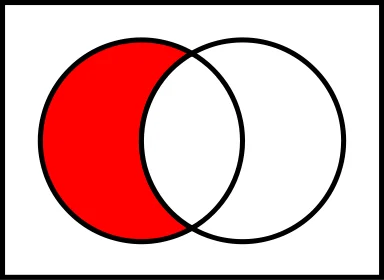

Contoh:
- {1, 2} \ {1, 2} = ∅.
- {1, 2, 3, 4} \ {1, 3} = {2, 4}.
Beberapa sifat dasar komplemen:
- A \ B ≠ B \ A untuk A ≠ B.
- A ∪ A′ = U.
- A ∩ A′ = ∅.
- (A′)′ = A.
- A \ A = ∅.
- U′ = ∅ dan ∅′ = U.
- A \ B = A ∩ B′.
Ekstensi dari komplemen adalah diferensi simetris (pengurangan himpunan), jika diterapkan untuk himpunan A dan B atau A – B menghasilkan
Contohnya, diferensi simetris antara:
- {7, 8, 9, 10} dan {9, 10, 11, 12} adalah {7, 8, 11, 12}.
- {Ana, Budi, Dedi, Felix} dan {Budi, Cici, Dedi, Ela} adalah {Ana, Cici, Ela, Felix}.
Notasi tanda himpunan matematika
Biasanya, nama himpunan ditulis menggunakan huruf besar, misalnya S, A, atau B, sementara anggota himpunan ditulis menggunakan huruf kecil (a, c, z). Cara penulisan ini adalah yang umum dipakai, tetapi tidak membatasi bahwa setiap himpunan harus ditulis dengan cara seperti itu. Tabel di bawah ini menunjukkan format penulisan himpunan yang umum dipakai.
| Nama | Notasi | Contoh |
|---|---|---|
| Himpunan | Huruf besar |  |
| Anggota himpunan | Huruf kecil (jika merupakan huruf) |  |
| Kelas | Huruf tulisan tangan |  |
Himpunan-himpunan bilangan yang cukup dikenal, seperti bilangan kompleks, riil, bulat, dan sebagainya, menggunakan notasi yang khusus.
| Bilangan | Asli | Bulat | Rasional | Riil | Kompleks |
|---|---|---|---|---|---|
| Notasi |  |  |  |  |  |
Simbol-simbol khusus yang dipakai dalam teori himpunan adalah:
| Simbol | Arti |
|---|---|
 atau atau  | Himpunan kosong |
 | Operasi gabungan dua himpunan |
 | Operasi irisan dua himpunan |
 , ,  , ,  , ,  | Subhimpunan, Subhimpunan sejati, Superhimpunan, Superhimpunan sejati |
 | Komplemen |
 | Himpunan kuasa |
Himpunan dapat didefinisikan dengan dua cara, yaitu:
- Enumerasi, yaitu mendaftarkan semua anggota himpunan. Jika terlampau banyak tetapi mengikuti pola tertentu, dapat digunakan elipsis (…).
- Pembangun himpunan, tidak dengan mendaftar, tetapi dengan mendeskripsikan sifat-sifat yang harus dipenuhi oleh setiap anggota himpunan tersebut.
Notasi pembangun himpunan dapat menimbulkan berbagai paradoks, contohnya adalah himpunan berikut:
Himpunan A tidak mungkin ada, karena jika A ada, berarti harus mengandung anggota yang bukan merupakan anggotanya. Namun jika bukan anggotanya, lalu bagaimana mungkin A bisa mengandung anggota tersebut.
Dalam himpunan dikenal adanya notasi. Notasi adalah penyimbolan dalam suatu himpunan.
Ada beberapa notasi yang sering dijumpai dalam himpunan, yaitu:
1. ![]() adalah notasi untuk himpunan bilangan Bulat.
adalah notasi untuk himpunan bilangan Bulat.
![]() ={…,-3,-2,-1,0,1,2,3,…}
={…,-3,-2,-1,0,1,2,3,…}
2. ![]() adalah notasi untuk himpunan bilangan Riil.
adalah notasi untuk himpunan bilangan Riil.
3. ![]() adalah notasi untuk himpunan bilangan Asli.
adalah notasi untuk himpunan bilangan Asli.
![]() ={1,2,3,4,5,6,7,…}
={1,2,3,4,5,6,7,…}
4. ![]() adalah notasi yang menunjukan anggota bagian suatu himpunan tertentu.
adalah notasi yang menunjukan anggota bagian suatu himpunan tertentu.
5. ![]() adalah notasi yang menunjukan bukan anggota bagian dari suatu himpunan tertentu.
adalah notasi yang menunjukan bukan anggota bagian dari suatu himpunan tertentu.
6. ![]() adalah notasi yang menunjukan himpunan bagian dari suatu himpunan tertentu.
adalah notasi yang menunjukan himpunan bagian dari suatu himpunan tertentu.
7. ![]() adalah notasi yang menunjukan himpunan bagian atau sama dengan suatu himpunan tertentu.
adalah notasi yang menunjukan himpunan bagian atau sama dengan suatu himpunan tertentu.
8. ![]() adalah notasi irisan dari suatu bilangan tertentu.
adalah notasi irisan dari suatu bilangan tertentu.
9. ![]() adalah notasi gabungan dari suatu bilangan tertentu.
adalah notasi gabungan dari suatu bilangan tertentu.
10. ![]() merupakan notasi dari himpunan kosong.
merupakan notasi dari himpunan kosong.
Himpunan kosong
Himpunan {apel, jeruk, mangga, pisang} memiliki anggota-anggota apel, jeruk, mangga, dan pisang. Himpunan lain, semisal {5, 6} memiliki dua anggota, yaitu bilangan 5 dan 6. Kita boleh mendefinisikan sebuah himpunan yang tidak memiliki anggota apa pun. Himpunan ini disebut sebagai himpunan kosong.
Himpunan kosong tidak memiliki anggota apa pun, ditulis sebagai:
Relasi Antar Himpunan Matematika
Himpunan bagian
Dari suatu himpunan, misalnya A = {apel, jeruk, mangga, pisang}, dapat dibuat himpunan-himpunan lain yang anggotanya adalah diambil dari himpunan tersebut.
- {apel, jeruk}
- {jeruk, pisang}
- {apel, mangga, pisang}
Ketiga himpunan di atas memiliki sifat umum, yaitu setiap anggota himpunan itu adalah juga anggota himpunan A. Himpunan-himpunan ini disebut sebagai himpunan bagian dari A.
Jadi dapat dirumuskan:
B adalah himpunan bagian dari A jika setiap anggota B juga terdapat dalam A.
Kalimat di atas tetap benar untuk B himpunan kosong. Maka
Untuk sembarang himpunan A,
Definisi di atas juga mencakup kemungkinan bahwa himpunan bagian dari A adalah A sendiri.
Untuk sembarang himpunan A,
Istilah subhimpunan dari A biasanya berarti mencakup A sebagai himpunan bagiannya sendiri. Kadang-kadang istilah ini juga dipakai untuk menyebut himpunan bagian dari A, tetapi bukan Asendiri. Pengertian mana yang digunakan biasanya jelas dari konteksnya.
Himpunan bagian sejati dari A menunjuk pada himpunan bagian dari A, tetapi tidak mencakup A sendiri.
Superhimpunan
Kebalikan dari subhimpunan adalah superhimpunan, yaitu himpunan yang lebih besar yang mencakup himpunan tersebut.
Kesamaan dua himpunan
Himpunan A dan B disebut sama, jika setiap anggota A adalah anggota B, dan sebaliknya, setiap anggota B adalah anggota A.
atau
Definisi di atas sangat berguna untuk membuktikan bahwa dua himpunan A dan B adalah sama. Pertama, buktikan dahulu A adalah subhimpunan B, kemudian buktikan bahwa B adalah subhimpunan A.
Himpunan Kuasa
Himpunan kuasa atau himpunan pangkat (power set) dari A adalah himpunan yang terdiri dari seluruh himpunan bagian dari A. Notasinya adalah
Jika A = {apel, jeruk, mangga, pisang}, maka 
{ { },
{apel}, {jeruk}, {mangga}, {pisang},
{apel, jeruk}, {apel, mangga}, {apel, pisang},
{jeruk, mangga}, {jeruk, pisang}, {mangga, pisang},
{apel, jeruk, mangga}, {apel, jeruk, pisang}, {apel, mangga, pisang}, {jeruk, mangga, pisang},
{apel, jeruk, mangga, pisang} }
Banyaknya anggota yang terkandung dalam himpunan kuasa dari A adalah 2 pangkat banyaknya anggota A.
Kelas atau Keluarga himpunan
Suatu himpunan disebut sebagai kelas, atau keluarga himpunan jika himpunan tersebut terdiri dari himpunan-himpunan.
Himpunan 

Contoh berikut, 
Kardinalitas
Kardinalitas dari sebuah himpunan dapat dimengerti sebagai ukuran banyaknya anggota yang dikandung oleh himpunan tersebut. Banyaknya anggota himpunan 
Himpunan 
Dua buah himpunan A dan B memiliki kardinalitas yang sama, jika terdapat fungsi korespondensi satu-satu yang memetakan A pada B.
Karena dengan mudah kita membuat fungsi 
Himpunan Denumerabel
Jika sebuah himpunan ekivalen dengan himpunan 
Kardinalitas dari himpunan tersebut disebut sebagai kardinalitas 
Himpunan semua bilangan genap positif merupakan himpunan denumerabel, karena memiliki korespondensi satu-satu antara himpunan tersebut dengan himpunan bilangan asli, yang dinyatakan oleh 
Himpunan Berhingga
Jika sebuah himpunan memiliki kardinalitas yang kurang dari kardinalitas 
Himpunan Tercacah
Himpunan disebut tercacah jika himpunan tersebut adalah berhingga atau denumerabel.
Himpunan Non-Denumerabel
Himpunan yang tidak tercacah disebut himpunan non-denumerabel. Contoh dari himpunan ini adalah himpunan semua bilangan riil. Kardinalitas dari himpunan jenis ini disebut sebagai kardinalitas 
Himpunan bilangan riil dalam interval (0,1) juga memiliki kardinalitas 

Fungsi Karakteristik Himpunan Matematika
Fungsi karakteristik menunjukkan apakah sebuah anggota terdapat dalam sebuah himpunan atau tidak.
Jika 
Terdapat korespondensi satu-satu antara himpunan kuasa 
Hal ini mengakibatkan kita dapat menuliskan himpunan sebagai barisan bilangan 0 dan 1, yang menyatakan ada tidaknya sebuah anggota dalam himpunan tersebut.
Representasi Biner dalam himpunan matematika
Jika konteks pembicaraan adalah pada sebuah himpunan semesta S, maka setiap himpunan bagian dari S bisa dituliskan dalam barisan angka 0 dan 1, atau disebut juga bentuk biner.
Bilangan biner menggunakan angka 1 dan 0 pada setiap digitnya. Setiap posisi bit dikaitkan dengan masing-masing anggota S, sehingga nilai 1 menunjukkan bahwa anggota tersebut ada, dan nilai 0 menunjukkan bahwa anggota tersebut tidak ada.
Dengan kata lain, masing-masing bit merupakan fungsi karakteristik dari himpunan tersebut.
Sebagai contoh, jika himpunan S = {a, b, c, d, e, f, g}, A = {a, c, e, f}, dan B = {b, c, d, f}, maka:
Himpunan Representasi Biner
---------------------------- -------------------
a b c d e f g
S = { a, b, c, d, e, f, g } --> 1 1 1 1 1 1 1
A = { a, c, e, f } --> 1 0 1 0 1 1 0
B = { b, c, d, f } --> 0 1 1 1 0 1 0
Cara menyatakan himpunan seperti ini sangat menguntungkan untuk melakukan operasi-operasi himpunan, seperti union (gabungan), interseksi (irisan), dan komplemen (pelengkap), karena kita tinggal menggunakan operasi bit untuk melakukannya. Representasi himpunan dalam bentuk biner dipakai oleh kompiler-kompiler Pascal dan juga Delphi.
Contoh Soal dan Jawaban Himpunan Matematika
1. Diketahui:
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3, 4, 5}
B = {6, 7, 8}
a. Tentukanlah A ∪ B.
b. Buatlah diagram Venn-nya.

2. Tuliskan himpunan-himpunan di bawah ini.
a. A adalah himpunan bilangan asli kurang dari 10.
b. M adalah nama-nama hari dalam seminggu.
Penyelesaian:
a. A = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
b. M = {Senin, Selasa, Rabu, Kamis, Jumat, Sabtu, Minggu}
3. Jika: M ={5 bilangan prima pertama}. Anggota dari M =…
Jawaban:
Bilangan prima: bilangan yang hanya mempunyai 2 faktor yaitu 1 dan bilangan itu sendiri.
5 bilangan prima pertama adalah {2,3,4,7,11}
4. Di ketahui:
A = { x | 1 < x < 20, maka x ialah bilangan prima }.
B = { y | 1 y 10, maka y ialah bilangan ganjil }.
Maka tentukanlah hasil dari A ∩ B ?
Jawaban nya :
A = { 2, 3, 5, 7, 11, 13, 16, 17, 19 }
B = { 1, 3, 5, 7, 9 }
Simbol yang artinya irisan ialah salah satu cara untuk himpunan anggota yang sama dari himpunan yang saling terkait.
A ∩ B = { 3, 5, 7 }
Jadi, hasil dari A ∩ B ialah = { 3, 5, 7 }.
5. Hitung banyaknya himpunan bagian dari bilangan ganjil kurang dari 5
Jawaban:
G = {1,3} n =2
{ }, {1}, {3}
{1,3}
Banyaknya ada 4
Cara rumus = 22 = 4
6. Jika A = {faktor dari 8} dan B = {bilangan prima kurang dari 12}, maka A ∩ B =….
Pembahasan:
A = {faktor dari 8}
A = {1, 2, 4, 8}
B = {bilangan prima kurang dari 12}
B = {2, 3, 5, 7, 11}
Tanda ∩ menyatakan irisan himpunan. Jadi A ∩ B adalah anggota A yang juga anggota B, maka A ∩ B = {2}
7. Hitung banyak himpunan bagian dari P = { 1, 2, 3, 5, 7}
Jawaban:
Gunakan cara rumus saja, n(P) = 5
Banyaknya himpunan bagian P = 2n=5 2 =32
8. Di dalam sebuah ruangan terdapat 150 siswa yang baru lulus SMP. Diketahui ada 75 siswa memilih untuk masuk SMA dan 63 siswa memilih untuk masuk SMK sementara ada 32 siswa yang belum menentukan pilihannya. Lalu, berapakah banyaknya siswa yang hanya memilih untuk masuk SMA dan SMK saja?
Pembahasan:
Siswa yang memilih masuk SMA dan SMK adalah:
n{AΛB} = (n{A} + n{B}) – (n{S} – n{X})
n{AΛB} = (75 + 63) – (150 – 32)
n{AΛB} = 138 – 118
n{AΛB} = 20 siswa
Siswa yang memilih masuk SMA saja = 75 – 20 = 55 orang
Siswa yang memilih masuk SMK saja = 63 – 20 = 43 orang
9. Tulis dalam bentuk himpunan kata-kata berikut.
a. NUSANTARA
b. MATEMATIKA.
Penyelesaian:
a. {N, U, S, A, T, R}
b. {M, A, T, E, I, K}
10. Hitung himpunan matematika bagian dari K= {1,2,3}
Cara manual
{ }, {1}, {2}, {3}
{1,2}, {1,3}, {2,3},
{1,2,3}
Jumlahnya ada 8
Menggunakan rumus
K= {1,2,3} n (K) = 3
Rumus
Banyaknya Himpunan Bagian =2n
=23
= 8
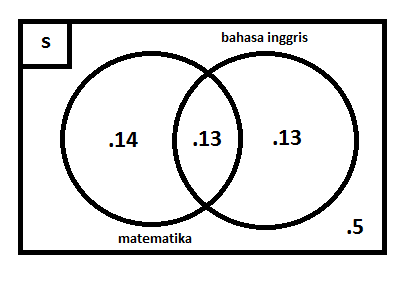
11. Siswa kelas 7 SMP Maju Jaya adalah 45. tiap-tiap siswa memilih dua jenis pelajaran yang mereka sukai. diketahui ada 27 siswa yang menyukai pelajaran Matematika dan 26 siswa menyukai pelajaran Bahasa Inggris. Sementara siswa yang tidak menyukai kedua pelajaran tersebut ada 5 orang. Tentukanlah banyaknya siswa yang menyukai pelajaran bahasa inggris dan matematika serta buat diagram venn-nya.
Pembahasan:
Cari terlebih dahulu jumlah siswa yang menyukai kedua pelajaran tersebut:
n{AΛB} = (n{A} + n{B}) – (n{S} – n{X})
n{AΛB} = (27 + 26) – (45 – 5)
n{AΛB} = 13
Maka dapat disimpulkan bahwa:
Siswa yang menyukai matematika saja = 27 – 13 = 14 siswa
Siswa yang menyukai bahasa inggris saja = 26 – 13 = 13 siswa
12. Dari 40 orang bayi, diketahui bahwa ada 18 bayi yang gemar memakan pisang, 25 bayi gemar makan bubur, dan 9 bayi menyukai keduanya. Lalu ada berapa bayi yang tidak menyukai pisang dan bubur?
Pembahasan:
n{AΛB} = (n{A} + n{B}) – (n{S} – n{X})
9 = (18 + 25) – (40 – n{X})
9 = 43 – 40 + n{X}
9 = 3 + n{X}
9 – 3 = n{X}
n{X} = 6
13. Diketahui himpunan A dan B seperti daftar berikut ini:
A = {1, 2, 4, 8}
B = {1, 2, 3, 4, 6, 12}
Tentukan:
a) A − B
b) B − A
Pembahasan:
A = {1, 2, 4, 8}
B = {1, 2, 3, 4, 6, 12}
a) A − B = {8}
Yakni dengan cara menuliskan ulang himpunan A sambil menghapus anggota A yang juga menjadi anggota dari B.
b) B − A = {3, 6, 12}
Yakni dengan cara menuliskan ulang himpunan B sambil menghapus anggota B yang juga menjadi anggota dari A.
14. Dari 42 kambing yang ada di kandang milik pak Tony, 30 kambing menyukai rumput gajah, dan 28 ekor kambing menyukai rumput teki. apabila ada 4 ekor kambing yang tidak menyukai kedua rumput tersebut, berapa ekor kambing yang menyukai rumput gajah dan rumput teki?
Pembahasan:
untuk mencarinya, kita gunakan rumus himpunan berikut:
n{AΛB} = (n{A} + n{B}) – (n{S} – n{X})
n{AΛB} = (30 + 28) – (42 – 4)
n{AΛB} = 58 – 38
n{AΛB} = 20
Jadi, jumlah kambing yang menyukai kedua jenis rumput tersebut adalah 20 ekor.
15. Himpunan matematika A, B dan C masing-masing anggotanya sebagai berikut:
A = {2, 3, 5, 7, 11, 13}
B = {0, 2, 4, 6, 8, 10, 12}
C = {1, 2, 3, 4, 6, 12}
Tentukanlah:
a)( A ∩ B) ∩ C
b) A ∩ (B ∩ C)
Kesimpulan apa yang dapat diambil?
Pembahasan:
a) Menentukan ( A ∩ B) ∩ C
A ∩ B = {2}
( A ∩ B) ∩ C = {2}
Menentukan A ∩ (B ∩ C)
B ∩ C = {2, 4, 6, 12}
A ∩ (B ∩ C) = {2}
Dapat disimpulkan bahwa ( A ∩ B) ∩ C = A ∩ (B ∩ C).
16. Diketahui semesata dari sebuah himpunan dan himpunan A sebagai berikut:
S = {x | 2 ≤ x ≤ 12 }
A = {3, 5, 7, 9, 11}
Tentukan komplemen dari himpunan A
Pembahasan:
Koplemen dari himpunan A adalah anggota semesta yang bukan anggota dari A. Sehingga:
A’ = {2, 4, 6, 8, 10, 12}
17. Di ketahui:
K = { x | 5 x 9, maka x ialah bilangan asli }.
L = { x | 7 x 13, maka x ialah bilangan cacah }.
Maka tentukanlah hasil dari K ∪ L ?
Jawaban:
K = { 5, 6, 7, 8, 9 }
L = { 7, 8, 9, 10, 11, 12, 13 }
Simbol ( union atau gabungan ) yang artinya ialah salah satu cara untuk menggabungkan anggota himpunan yang saling terkait.
K ∪ L = { 5, 6, 7, 8, 9, 10, 11, 12, 13 }
Jadi, hasil dari K ∪ L ialah = { 5, 6, 7, 8, 9, 10, 11, 12, 13 }.
18. Dari sekelompok atlet diketahui bahwa 17 orang menyukai sepak bola, 13 menyukai renang, dan 12 orang menyukai keduanya. coba kalian gambarkan diagram venn dan tentukan pula jumlah keseluruhan dari atlet tersebut.
Pembahasan:
Jumlah keseluruhan dari atlet tersebt adalah:
Atlet ang menyukai sepakbola saja : 17-12 = 5 orang
Atlet yang menyukai renang saja = 13 – 12 = 1 orang
Diagram venn-nya adalah:
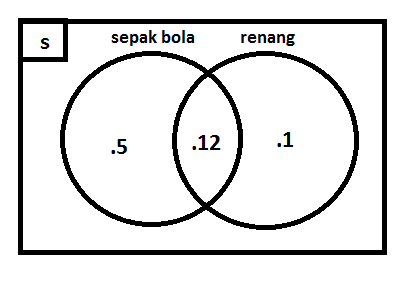
Jadi, jumlah keseluruhan atlet tersebut adalah 18 orang.
19. Diberikan himpunan A dan B sebagai berikut:
A = {2, 3, 5, 7, 9}
B = {0, 1, 2, 5, 10}
Tentukan:
a) A ∩ B
b) A ∪B
Pembahasan:
A = {2, 3, 5, 7, 9}
B = {0, 1, 2, 5, 10}
a) A ∩ B = {2, 5}
yakni irisan himpunan A dan himpunan B. Dituliskan anggota yang menjadi elemen dari kedua himpunan.
b) A ∪B = {0, 1, 2, 3, 5, 7, 9, 10}
Yakni gabungan himpunan A dan B. Dituliskan semua anggota yang ada pada kedua himpunan. Anggota yang sama dituliskan satu kali saja.
20. Di ketahui:
A = { x | 1 < x 5, maka x ialah bilangan bulat }.
B = { x | x 5, maka x ialah bilangan prima }.
Maka tentukanlah hasil dari A ∪ B ?
Jawaban:
A = { 2, 3, 4 ,5 }.
B = { 2, 3, 5, 7, 11, 13 }.
Simbol dari ( union atau gabungan ) yang artinya ialah salah satu cara untuk menggabungkan anggota himpunan yang saling terkait.
A ∪ B = { 2, 3, 4, 5, 7, 11, 13 }.
Jadi, hasil dari A ∪ B ialah = { 2, 3, 4, 5, 7, 11, 13 }.
21. Jika Diketahui: A= {1, 2, 3, 4, 5}
B = {2, 3, 6, 7, 8}
C = {4, 5, 6, 7, 8}
Tentukanlah:
a. A ∩ B c. B ∩ C
b. A ∩ C d. A ∩ B ∩ C
Jawab :
a. A ∩ B = {2, 3} c. B ∩ C = {6, 7, 8}
b. A ∩ C = {4, 5} d. A ∩ B ∩ C = { }
22. Diketahui sebuah P = { h, e, l, l, o }. Banyaknya himpunan dari bagian P tadi ialah?
Jawaban:
Banyaknya anggota dari P yakni n( P ) = 5
Banyaknya himpunan dari bagian P bisa diketahui dengan menggunakan rumus seperti di bawah ini:
2n( P )
Maka caranya ialah seperti ini:
= 2n( P )
= 25
= 32
jadi, hasil banyaknya himpunan dari bagian P tadi ialah = 32.
Di ketahui :
A = { x | 1 < x < 20, maka x ialah bilangan prima }.
B = { y | 1 y 10, maka y ialah bilangan ganjil }.
Maka tentukanlah hasil dari A ∩ B ?
Jawaban nya :
A = { 2, 3, 5, 7, 11, 13, 16, 17, 19 }
B = { 1, 3, 5, 7, 9 }
Simbol yang artinya irisan ialah salah satu cara untuk himpunan anggota yang sama dari himpunan yang saling terkait.
A ∩ B = { 3, 5, 7 }
Jadi, hasil dari A ∩ B ialah = { 3, 5, 7 }.
Bacaan Lainnya
- Rumus Trigonometri Dan Contoh-Contoh Soal Beserta Jawabannya
- Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
- Perasaan Remaja – Apa yang Anda rasakan?
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Pada Daerah Kewanitaan Akibat Pembalut Wanita
- Apakah Produk Pembalut Wanita Aman?
- 10 Cara Menjadi Lebih Pintar Dengan Cepat Dan Menaikan IQ & Terbukti Secara Ilmiah
- Tes Matematika Deret Angka – Hanya Untuk Yang Jenius: Jika 8 = 56, 7 = 42, 6 = 30, 5 = 20, Jadi 3 = ?
- Tes Matematika Deret Angka: Bersama Cara Menghitung Kuadrat Dan Akar Kuadrat
- 10 Cara Dan Strategi Melawan Stres Yang Efektif & Terbukti Secara Ilmiah
- Fungsi, Perbedaan, Cara Berpikir Otak Kiri Dan Kanan
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Tutorials Point, Britannica
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz |Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing