Penjumlahan dan Pengurangan Bentuk Aljabar

Bentuk aljabar yang dapat dijumlahkan atau dikurangkan yaitu hanya pada bentuk aljabar yang memiliki suku yang sama. Dalam penjumlahan dan pengurangan yang dijumlah ataupun dikurangkan adalah koefisiennya dalam suku yang sama .

Rumus Penjumlahan Bentuk Aljabar

an + bn = ( a + b ) n

Rumus Pengurangan Bentuk Aljabar

an – bn= ( a – b ) n

Keterangan :

a dan b = koefisien
n = Variabel

Penjelasan Aljabar

Adalah salah satu bagian dari bidang matematika yang luas, bersama-sama dengan teori bilangan, geometri dan analisis. Rumus Aljabar merupakan salah satu rumpun matematika yang penting, karena manfaatnya yang besar dalam memahami konsep lain ilmu matematika.

Aljabar dimulai dengan perhitungan yang sama dengan aritmetika, dengan huruf digunakan untuk mewakili angka. hal Ini memungkinkan bukti dari sifat-sifat yang benar tanpa memperhatikan angka-angka yang terlibat.

Rumus kuadrat aljabar:

ax² + bx + c = 0

$a,b,c$ bisa menjadi bilangan apapun (kecuali bahwa $a$ tidak dapat bernilai $0$ ), dan rumus kuadrat dapat digunakan untuk dengan cepat dan mudah menemukan nilai-nilai dari kuantitas $x$ yang tidak diketahui dan memenuhi persamaan. Rumus kuadrat digunakan untuk menyatakan persamaan, dan kemudian menemukan semua solusi dari persamaan tersebut.

Operasi bentuk aljabar

operasi hitung dalam aljabar , sama halnya dengan operasi hitung bilangan bulat yaitu meliputi :

1. Penjumlahan bentuk aljabar

2. Pengurangan bentuk aljabar

3. Perkalian bentukaljabar

4. Pembagian bentuk aljabar

5. Perpangkatan bentuk aljabar

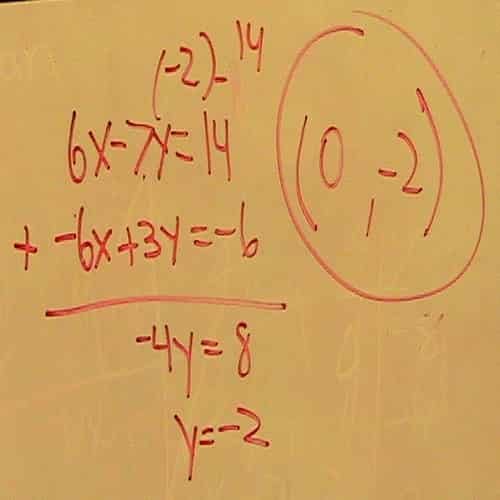
Istilah – istilah yang perlu di pahami dalam bentuk aljabar

Istilah – istilah ini merupakan unsur – unsur yang terdapat dalam bentuk aljabar , unsur – unsur tersebut adalah :

1. Variabel disebut juga dengan peubah , yang memiliki pengertian lambang pengganti bilangan yang belum di ketahui . Contoh variabel : x , y , a , b , xy

2. Koefisien yaitu angka yang terdapat di depan variabel .

contoh : x+3 = koefisiennya adalah 1 , 3x+5 = koefisiennya adalah 3

3. Konstanta ,yaitu suku dari suatu bentuk aljabar yang berdiri sendiri

contoh : 4x + 5y + 6 , maka konstanta dari bentuk aljabar tersebut adalah 6

4. Suku , yaitu nilai yang menyusun suatu bentuk aljabar yang berupa variabel , koefisien ataupun konstanta .

macam – macam suku :

1. Menurut jenisnya :

Suku sejenis , yaitu bentuk aljabar yang variabel dan pangkatnya sama contoh : 3x dan x , 3xy dan xy
suku tak sejenis , yaitu bentuk aljabar yang variabel dan pangkatnya tak sama .contoh : 4x dan 4y , 2xy dan 3xy², 2xy dan x

2. Menurut jumlah sukunya :

suku satu , yaitu bentuk aljabar yang berdiri sendiri yang tidak dihubungkan oleh operasi penjumlahan ataupun selisih . contoh x , 2x
suku dua , yaitu bentuk aljabar yang dihubungkan oleh operasi penjumlahan ataupun selisih . contoh: x+y , 3x- y
suku tiga , yaitu bentuk aljabar yang dihibungkan oleh 2 operasi penjumlahan ataupun selisih . contoh : x+y+7, 2x+2xy+2

Aljabar elementer

Notasi ekspresi aljabar:
1 – pangkat (power)
2 – koefisien
3 – suku (term)
4 – operator
5 – suku konstanta
x y c – variabel/konstanta

Aljabar elementer adalah bentuk aljabar paling dasar. Aljabar elementer diajarkan kepada siswa/mahasiswa yang dianggap tidak memiliki pengetahuan tentang matematika lebih dari sekadar prinsip-prinsip dasar aritmetika. Di dalam aritmetika, hanya bilangan dan operasi aritmetika (seperti +, −, ×, ÷) yang muncul. Di dalam aljabar, bilangan seringkali diwakili oleh simbol, yang disebut variabel (seperti a, n, x, y, atau z). Ini berguna, karena:

Ini membolehkan perumusan umum dari hukum-hukum aritmetika (seperti a + b = b + a untuk setiap a dan b), dan dengan demikian merupakan langkah pertama menuju eksplorasi sistematis pada sifat-sifat sistem bilangan real.
Ini membolehkan referensi bagi bilangan “anu”, perumusan persamaan dan pengkajian cara untuk menyelesaikannya. (Misalnya, “Carilah bilangan x sedemikian sehingga 3x+ 1 = 10″ atau lebih lanjut “Carilah bilangan x sedemikian sehingga ax + b = c“. Langkah ini mengarah pada kesimpulan bahwa bukanlah sifat alami bilangan tertentu yang membolehkan kita menyelesaikannya, melainkan operasi yang dilibatkan.)
Ini mengizinkan perumusan hubungan fungsional. (Misalnya, “Jika Anda menjual x karcis, maka keuntunganmu sebesar 3x − 10 rupiah, atau f(x) = 3x − 10, di mana f adalah fungsi, dan x adalah bilangan yang terhadapnya fungsi ini diterapkan”.)

Dalam aljabar elementer, sebuah “pernyataan matematika” boleh terdiri dari bilangan, variabel, dan operasi aritmetika. Ini biasanya ditulis dengan ‘pangkat yang lebih tinggi’ diletakkan di kiri; contohnya:

x+3\,

y^{2}+2x-3\,

z^{7}+a(b+x^{3})+42/y-\pi .\,

Dalam aljabar yang lebih lanjut, suatu pernyataan juga mungkin memiliki fungsi elementer.
Sebuah “persamaan” adalah klaim bahwa dua pernyataan adalah sama. Sebagian persamaan berlaku untuk semua nilai variabel (seperti a + b = b + a). Persamaan seperti ini dinamakan “identitas”. Persamaan “bersyarat” berlaku hanya untuk sebagian nilai variabel yang mungkin: x² − 1 = 4. Nilai-nilai variabel yang membuat persamaan tersebut berlaku disebut pemecahan atau “solusi” persamaan.

Polinomial

Grafik fungsi polinomial berderajat 3.

Polinomial atau suku banyak adalah sebuah ekspresi yang merupakan jumlah bilangan berhingga dari suku-suku tak-nol, tiap-tiap suku memuat perkalian dari sebuah konstanta dan sejumlah berhingga variabel yang muncul dengan seluruh pangkat bilangan. Misalnya, x² + 2x − 3 adalah polinomial dalam variabel tunggal x. Sebuah ekspresi polinomial adalah ekspresi yang dapat ditulis ulang sebagai polinomial, dengan menggunakan sifat-sifat komutativitas, asosiativitas, dan distributivitas perjumlahan dan perkalian. Misalnya, (x − 1)(x + 3) adalah sebuah ekspresi polinomial. Sebuah fungsi polinomial adalah fungsi yang didefinisikan oleh polinomial, atau, secara ekivalen, oleh sebuah ekspresi polinomial. Dua contoh tersebut mendefinisikan fungsi polinomial yang sama.

Dua soal yang penting dan berhubungan di dalam aljabar adalah faktorisasi polinomial, yaitu, mengekspresikan suatu polinomial sebagai perkalian dari polinomial-polinomial lainnya yang tidak dapat difaktorkan lagi, dan komputasi faktor persekutuan terbesar polinomial. Contoh polinomial di atas dapat difaktorkan sebagai (x − 1)(x + 3). Sebuah kelas soal yang behubungan adalah pencarian ekspresi aljabar untuk akar suatu polinomial dalam variabel tunggal.

Aljabar abstrak

Aljabar abstrak memperluas konsep-konsep yang biasa ditemukan dalam aljabar elementer dan aritmetika bilangan ke konsep-konsep yang lebih umum. Yang berikut ini adalah konsep-konsep dasar di dalam aljabar abstrak.

Himpunan

Lebih dari sekadar memperhatikan jenis-jenis bilangan yang berbeda-beda, aljabar abstrak berurusan dengan konsep himpunan yang lebih umum: sekumpulan objek-objek (disebut elemen) yang dipilih oleh sifat spesifik untuk himpunan. Semua kumpulan jenis-jenis bilangan yang lazim dikenal merupakan himpunan. Contoh himpunan lainnya adalah himpunan semua matrikss dua-kali-dua, himpunan semua polinomialberderajat 2 (ax² + bx + c), himpunan semua vektor dua dimensi pada bidang, dan berbagai grup berhingga seperti grup siklis, yang merupakan grup-grup modulo bilangan bulat n. Teori himpunan adalah sebuah cabang dari logika dan secara teknis bukanlah cabang dari aljabar.

Operasi biner

Maksud perjumlahan (+) diabstraksi untuk memberikan sebuah operasi biner, katakanlah ∗. Maksud operasi biner menjadi tidak berarti tanpa adanya himpunan tempat operasi didefinisikan. Untuk dua elemen a dan b dalam himpunan S, a ∗ b adalah elemen lain di dalam himpunan; kondisi ini disebut ketertutupan. Perjumlahan (+), perkurangan (−), perkalian (×), dan perbagian (÷) dapat menjadi operasi biner ketika terdefinisi pada himpunan yang berbeda, semisal perjumlahan dan perkalian matriks, vektor, dan polinomial.

Contoh yang khas dari operasi biner adalah penjumlahan (+) dan perkalian (×) dari bilangan dan matrik serta komposisi fungsi pada satu set. Misalnya,

Pada himpunan bilangan real R, f(a, b) = a + b adalah operasi biner karena jumlah dari dua bilangan real adalah bilangan real.
Pada himpunan bilangan asli N, f(a, b) = a + b adalah operasi biner karena jumlah dari dua bilangan asli adalah bilangan asli. Ini adalah operasi biner yang berbeda dari yang sebelumnya karena himpunan yang berbeda.
Pada himpunan M(2,2), matriks 2 × 2 dengan entri-entri bilangan real, f(A, B) = A + B adalah operasi biner karena jumlah dari dua matriks tersebut adalah matriks 2 × 2 .
Pada himpunan M(2,2), matriks 2 × 2 dengan entri-entri bilangan real, f(A, B) = AB adalah operasi biner karena produk dari kedua matriks tersebut adalah matriks 2 × 2 .
Untuk himpunan C, misalkan S adalah himpunan semua fungsi h : C → C. Definisikan f : S × S → S dengan f(h₁, h₂)(c) = h₁ ∘ h₂ (c) = h₁(h₂(c)) untuk semua c ∈ C, komposisi dari dua fungsi h₁ dan h₂ di S. Maka fadalah operasi biner karena komposisi dari dua fungsi adalah fungsi lain pada set C (artinya, anggota dari S).

Elemen identitas

Bilangan nol dan satu diabstraksi untuk memberikan arti suatu elemen identitas untuk sebuah operasi. Nol adalah elemen identitas untuk perjumlahan dan satu adalah elemen identitas untuk perkalian. Untuk suatu operator biner umum ∗ elemen identitas e harus memenuhi a ∗ e = a dan e ∗ a = a, dan harus tunggal, jika ia ada. Ini berlaku untuk perjumlahan sebagai a + 0 = a dan 0 + a = a dan perkalian a × 1 = a dan 1 × a = a. Tidak semua himpunan dan kombinasi operator memiliki elemen identitas; misalnya, himpunan bilangan asli positif (1, 2, 3, …) tidak memiliki elemen identitas untuk perjumlahan.

Elemen invers atau unsur balikan

Bilangan negatif memunculkan konsep elemen invers. Untuk perjumlahan, invers a ditulis sebagai −a; dan untuk perkalian, invers ditulis sebagai a⁻¹. Elemen invers umum untuk dua-pihak a⁻¹ memenuhi sifat bahwa a ∗ a⁻¹ = e dan a⁻¹ ∗ a = e, di mana e adalah elemen identitas.

Asosiativitas

Perjumlahan bilangan bulat memiliki sifat yang dinamakan asosiativitas. Yakni, pengelompokan bilangan yang dijumlahkan tidaklah mengubah hasilnya. Misalnya: (2 + 3) + 4 = 2 + (3 + 4). Secara umum, ini menjadi (a ∗ b) ∗ c = a ∗ (b ∗ c). Sifat ini juga berlaku pada sebagian besar operasi biner, tetapi tidak untuk perkurangan, atau perbagian, atau perkalian oktonion.

Komutativitas

Perjumlahan dan perkalian bilangan real sama-sama bersifat komutatif. Yakni, urutan bilangan tidaklah mengubah hasil. Misalnya: 2 + 3 = 3 + 2. Secara umum, ini menjadi a ∗ b = b ∗ a. Sifat ini tidak berlaku untuk semua operasi biner. Misalnya, perkalian matriks dan perkalian kuaternion, kedua-duanya tidak bersifat komutatif.

Grup

Penggabungan konsep-konsep di atas memberikan salah satu struktur yang paling penting dalam matematika: grup. Grup adalah kombinasi dari sebuah himpunan S dan satu operasi biner ∗, didefinisikan dalam cara apapun yang dipilih, tapi dengan sifat sebagai berikut:

Terdapat sebuah elemen identitas e, sedemikian sehingga untuk setiap anggota a dari S, e ∗ a dan a ∗ e kedua-duanya identik dengan a.
Setiap elemen mempunyai invers: untuk setiap anggota a dari S, terdapat anggota a^-1 sedemikian sehingga a ∗ a^-1 dan a^-1 ∗ a kedua-duanya identik dengan elemen identitas.
Operasi bersifat asosiatif: jika a, b, dan c adalah anggota dari S, maka (a ∗ b) ∗ c identik dengan a ∗ (b ∗ c).

Jika grup ini juga komutatif, yaitu untuk setiap dua anggota a dan b dari S, a ∗ b adalah identik untuk b ∗ a—maka grup tersebut dikatakan abelian.

Sebagai contoh, himpunan bilangan bulat di bawah operasi perjumlahan merupakan grup. Dalam grup ini, elemen identitas adalah 0 dan invers dari setiap elemen a adalah negasinya, −a. Persyaratan asosiativitas terpenuhi, karena untuk setiap bilangan bulat a, b, dan c, (a + b) + c = a + (b + c)

Bilangan rasional tak-nol membentuk grup di bawah operasi perkalian.

Di sini, elemen identitas adalah 1, karena 1 × a = a × 1 = a untuk setiap bilangan rasional a. Invers dari a adalah 1/a, karena a × 1/a = 1.

Meskipun demikian, bilangan bulat di bawah operasi perkalian tidaklah membentuk sebuah grup. Hal ini karena invers perkalian suatu bilangan bulat tidaklah menghasilkan bilangan bulat. Misalnya, 4 adalah bilangan bulat, tetapi invers perkaliannya adalah ¼, yang tentu saja bukan merupakan bilangan bulat.

Teori mengenai grup dipelajari dalam teori grup. Hasil utama dalam teori ini adalah klasifikasi grup-grup sederhana berhingga, sebagian besar diterbitkan antara tahun 1955 dan tahun 1983, yang memisahkan grup-grup sederhana berhingga menjadi kira-kira 30 jenis dasar.

Semigrup, kuasigrup, dan monoid adalah struktur-struktur yang serupa dengan grup, tetapi bersifat lebih umum. Mereka memuat sebuah himpunan dan satu operasi biner tertutup, tetapi tidak perlu memenuhi persyaratan lainnya. Semigrup memiliki operasi biner asosiatif, tetapi tidak memiliki elemen identitas. Monoid adalah semigrup yang memiliki elemen identitas, tetapi tidak memiliki invers untuk setiap elemen. Kuasigrupmemenuhi persyaratan bahwa sembarang elemen dapat diubah menjadi elemen yang lain dengan perkalian-kiri atau perkalian-kanan yang tunggal; tetapi operasi binernya mungkin tidak bersifat asosiatif.

Semua grup adalah monoid dan semua monoid adalah semigrup. Contohnya

Himpunan	Bilangan asli N		Bilangan bulat Z		Bilangan rasional Q (juga Bilangan real R dan kompleks C)				Modulo bilangan bulat 3: Z₃ = {0, 1, 2}
Operasi	+	× (tak-nol)	+	× (tak-nol)	+	−	× (tak-nol)	÷ (tak-nol)	+	× (tak-nol)
Tertutup	Ya	Ya	Ya	Ya	Ya	Ya	Ya	Ya	Ya	Ya
Identitas	0	1	0	1	0	Tidak ada	1	Tidak ada	0	1
Invers	Tidak ada	Tidak ada	−a	Tidak ada	−a	Tidak ada	1/a	Tidak ada	masing-masing: 0, 2, 1	masing-masing: Tidak ada, 1, 2
Asosiatif	Ya	Ya	Ya	Ya	Ya	Tidak	Ya	Tidak	Ya	Ya
Komutatif	Ya	Ya	Ya	Ya	Ya	Tidak	Ya	Tidak	Ya	Ya
Struktur	monoid	monoid	grup abelian	monoid	grup abelian	kuasigrup	grup abelian	kuasigrup	grup abelian	grup abelian (Z₂)

Gelanggang dan medan

Grup hanya memiliki satu operasi biner. Untuk menjelaskan sepenuhnya perilaku jenis-jenis bilangan yang berbeda, struktur-struktur dengan dua operator haruslah dipelajari. Yang paling penting darinya adalah gelanggang, dan medan.

Sebuah gelanggang memiliki dua operasi biner (+) dan (×), dengan × distributif di atas +. Di bawah operator pertama (+), ia membentuk grup abelian. Di bawah operator kedua (×), ia bersifat asosiatif, tetapi tidak harus memiliki identitas, atau invers, sehingga perbagian tidaklah diperlukan. Elemen identitas perjumlahan (+) ditulis sebagai 0 dan invers perjumlahan dari a ditulis sebagai −a.

Sifat distributif memperumum hukum distributif untuk bilangan. Untuk bilangan bulat (a + b) × c = a × c + b × c dan c × (a + b) = c × a + c × b, dan × dikatakan distributif di atas +.

Bilangan bulat adalah contoh dari gelanggang. Bilangan bulat memiliki sifat-sifat perjumlahan yang membuatnya sebagai domain integral, atau ranah bilangan bulat.

Sebuah medan adalah gelanggang dengan sifat perjumlahan bahwa semua elemen tak-nol membentuk grup abelian di bawah ×. Identitas perkalian (×) ditulis sebagai 1 dan invers perkalian dari a ditulis sebagai a⁻¹.

Bilangan rasional, bilangan real dan bilangan kompleks adalah contoh-contoh medan.

Unsur pada Bentuk Aljabar

Variabel, Konstanta, Koefisien & Faktor

Perhatikan contoh berikut :

$3x+2y+7p-10 \$ dan $p =2x+y \$

Penjelasan :

$x \$ dan $y \$ adalah variabel
$p \$ adalah faktor, karena $p \$ mengandung variabel $x \$ dan $y, p =2x+y \$
10 adalah konstanta
3 adalah koefisien dari $x \$
2 adalah koefisien dari $y \$ , dan
7 adalah koefisien dari $p \$

Kesimpulannya :

variabel adalah huruf sebagai simbol pengganti bilangan yang belum diketahui besarnya
konstanta adalah bilangan yang tidak memuat variabel
faktor adalah huruf atau simbol sebagai pengganti bilangan yang di dalamnya mengandung variabel
koefisien adalah besarnya bilangan yang merupakan konstanta dari variabel dalam bentuk aljabar

Suku Sejenis dan Suku Tak Sejenis

Perhatikan contoh berikut :

$3x+2y-7p-10+4x^{3}-4y^{2}+4x+7y-2 \$

Penjelasan :

$3x, 2y, -7p, 4x^{3}, -4y^{2}, 4x, 7y \$ adalah suku
$3x \ \textup{dan} \ 4x, 2y \ \textup{dan} \ 7y \$ adalah suku sejenis
$3x \ \textup{dan} \ 2y, -7p \ \textup{dan} \ -4y^{2} \$ adalah suku tak sejenis

Kesimpulan :

Suku adalah variabel beserta koefisien dalam bentuk aljabar yang dipisahkan oleh operasi penjumlahan atau selisih.
Suku sejenis adalah suku yang memiliki variabel yang sama
Suku tak sejenis adalah suku yang memiliki variabel yang berbeda.

Suku Satu, Suku Dua, Suku Tiga dan Suku Banyak

Suku Satu adalah bentuk aljabar yang tidak dipisahkan oleh operasi penjumlahan atau pengurangan.

Contohnya : $2x, 2y, 3x^{2} \$

Suku Dua adalah bentuk aljabar yang dipisahkan oleh 1 operasi penjumlahan atau pengurangan.

Contohnya : $2x + y, 2y - 3, 7x - 3x^{2} \$

Suku Tiga adalah bentuk aljabar yang dipisahkan oleh 2 operasi penjumlahan atau pengurangan.

Contohnya : $2x + y -1, 7x+ 2xy - 3, 7xy + 2y - 3x^{2} \$

Suku Banyak adalah bentuk aljabar yang dipisahkan oleh $n - 1 \$ operasi penjumlahan atau pengurangan.

Contohnya : $a_n x^{n}+a_{n-1} x^{n-1} + ... +a_2 x^{2}+a_1 x+a_0 \$

Operasi Perhitungan pada Bentuk Aljabar

Operasi Penjumlahan dan Pengurangan

Operasi penjumlahan dan pengurangan pada bentuk aljabar, hanya dapat dilakukan pada suku – suku yang sejenis, yaitu dengan cara menjumlahkan atau mengurangkan koefisien dari variabel yang sejenis.

Contohnya :

$2x + x = 3x \$
$\Rightarrow 7z - 5z = (7 - 5)z = 2z \$
$2x + y -x \$
$\Rightarrow 2x - x + y \$
$\Rightarrow (2-1)x + y \$
$\Rightarrow x + y \$
$5x^{2} + 2y - x^{2} + 3z - 5y -5z - 2x^{2} \$
$\Rightarrow 5x^{2} - x^{2} - 2x^{2} + 2y - 5y + 3z -5z \$
$\Rightarrow (5 - 1 - 2)x^{2} + (2 - 5)y + (3 - 5)z \$
$\Rightarrow 2x^{2} +(-3)y + (-2)z \$
$\Rightarrow 2x^{2} - 3y -2z \$

Operasi Perkalian pada Bentuk Aljabar

Perkalian dalam bentuk aljabar juga berlaku sifat perkalian bilangan bulat, yaitu :

sifat tertutup
sifat komutatif (pertukaran)
sifat asosiatif (pengelompokan)
sifat distributif

Contoh sifat tertutup:

$7 \times p = 7p \$
$(-2) \times 3r = -6r \$
$4 \times (-8)q \times 2p= -64pq \$
$2x \times (-3)y \times (-4)z= 24xyz \$

Contoh sifat komutatif (pertukaran):

$7 \times p = p \times 7 = 7p \$
$(-2) \times 3r = 3r \times (-2) = -6r \$

Contoh sifat asosiatif (pengelompokan):

$(4 \times (-8)q) \times 2p= 4 \times ((-8)q \times 2p)= -64pq \$
$(2x \times (-3)y) \times (-4)z= 2x \times ((-3)y \times (-4)z) = 24xyz \$

Contoh sifat distributif:

Sifat Distributif Perkalian terhadap Penjumlahan dan Pengurangan :

$p \times ( a + b) = (p \times a) + (p \times b) \$
$p \times ( a - b) = (p \times a) - (p \times b) \$
$(p+q) \times ( a + b) = p\times a + p\times b + q\times a + q\times b = pa + pb + qa +qb \$
$(p+q) \times ( a - b) = p\times a + p\times (-b) + q\times a + q \times (-b) = pa - pb + qa - qb \$
$(p-q) \times ( a - b) = p \times a + p\times (-b) -q\times a -q \times (-b) = pa - pb - qa + qb \$

Contoh soal:

$p \times (2 + 3) \$
$\Rightarrow (p \times 2) + (p \times 3) \$
$\Rightarrow 2p + 3p = 5p \$
$x \times ((-2) + 3) \$
$\Rightarrow (x \times (-2)) + (x \times 3) \$
$\Rightarrow (-2)p + 3p = p \$
$q \times (7 - 3) \$
$\Rightarrow (q \times (7)) - (q \times 3) \$
$\Rightarrow 7q - 3q = 4q \$
$y \times (7 - (-2)) \$
$\Rightarrow (y \times (7)) - (y \times (-2)) \$
$\Rightarrow 7y - (-2y) = 9y \$
$(p+2)\times (p+1) \$
$\Rightarrow p^{2} + p +2p +2 \$
$\Rightarrow p^{2}+3p+2 \$
$(p+2q)\times (p-3q) \$
$\Rightarrow p^{2} - 3pq +2pq -6q^{2} \$
$\Rightarrow p^{2} - pq - 6q^{2} \$

Operasi Perpangkatan dalam Bentuk Aljabar

Bentuk bilangan berpangkat atau disebut juga bentuk eksponen merupakan cara praktis dan ringkas untuk menuliskan perkalian dan pembagian dari bilangan – bilangan dengan faktor – faktor yang sama.

Pangkat atau eksponen dapat berupa bilangan positif, negatif, nol atau bilangan rasional lainnya.

PENGERTIAN BILANGAN BERPANGKAT

Perhatikan contoh berikut :

$2^{5}=2 \times 2 \times 2 \times 2 \times 2\$ ,

artinya 2 dikali 2 sebanyak 5 kali

$3^{7}=3 \times 3 \times 3 \times 3 \times 3 \times 3 \times 3 \$ ,

artinya 3 dikali 3 sebanyak 7 kali

atau,

$a^{n}=a \times a \times a \ ...\times a$ ,

artinya a dikali a sebanyak n-kali

Notasi $a^{n} \$ dibaca a pangkat n
$a \$ disebut bilangan pokok dari $a^{n} \$
$n \$ disebut pangkat atau eksponen dari $a \$

SIFAT – SIFAT BILANGAN DENGAN PANGKAT

$a^{m} \times a^{n} = a^{m+n} \$
$\frac{a^{m}}{a^{n}}=a^{m-n} \$
$(a^{m})^{n}=a^{m\times n} \$
$(ab)^{m}=a^{m}\times b^{m} \$
$(\frac{a}{b})^{n}=\frac{a^{n}}{b^{n}}, b \neq 0 \$
$a^{-n}=\frac{1}{a^{n}} \ \textup{atau} \ a^{n}=\frac{1}{a^{-n}} \$
$a^{0}=1 \$

Contoh Soal

$\frac{x^{6}}{x^{9}} \$ $\Rightarrow \frac{1}{x^{9-6}} \$
$\Rightarrow \frac{1}{x^{3}} \$
$\Rightarrow x^{-3} \$
$(pq^{2})^{3}= \$
$\Rightarrow p^{3}q^{2\times 3} \$
$\Rightarrow p^{3}q^{6} \$
$(\frac{2a^{2}}{b})^{3}= \$
$\Rightarrow \frac{2^{3}a^{2\times 3}}{b^{3}} \$
$\Rightarrow \frac{8a^{6}}{b^{3}} \$
$\Rightarrow 8a^{6}b^{-3} \$

Operasi Pembagian dalam Bentuk Aljabar

Dalam memahami operasi pembagian dalam bentuk aljabar, bisa kita ambil sifat pangkat negatif (-) seperti yang telah dijelaskan sebelumnya, dimana

$a^{-1}=\frac{1}{a} \$

Dengan demikian, mengacu dari sifat pangkat tersebut, untuk memahami lebih lanjut, mari simak contoh soal operasi pembagian bentuk aljabar sebagai berikut :

$\frac{x^{5}}{xy^{2}}=$
$\Rightarrow \frac{x^{5-1}}{y^{2}}$
$\Rightarrow \frac{x^{4}}{y^{2}}$
$\Rightarrow x^{4}y^{-2}$
$\frac{x^{2}y^{5}}{x^{3}y}=$
$\Rightarrow x^{2-3}y^{5-1}$
$\Rightarrow x^{-1}y^{4}$
$(a-b)^{-3}(\frac{a+b}{b-a})^{-2}\frac{1}{(a+b)^{-3}}=$
$\Rightarrow \frac{1}{(a-b)^{3}}\frac{(a+b)^{-2}}{(b-a)^{-2}}(a+b)^{3}$
$\Rightarrow \frac{(-a+b)^2}{(a-b)^3}(a+b)^{3-2}$
$\Rightarrow \frac{(-1)^{2}(a-b)^2}{(a-b)^3}(a+b)$ $\Rightarrow (a-b)^{2-3}(a+b)$
$\Rightarrow (a-b)^{-1}(a+b)$
$\ \Rightarrow\frac{a+b}{a-b}$

Contoh Soal Aljabar dan Jawaban

1. Soal: 7x + 3x = ?

Jawaban: 7x + 3x = (7+3)x = 10x

2. Tentukan koefisien dari bentuk – bentuk aljabar berikut:
a. 2x² + x – 1
b. 3x² +- 2x + 1
c. x² + 5x – 6
d. ax³+ bx² + cx + d

Jawab :

a. koefisien x² = 2 dan x = 1
b. koefisien  x²= 3 dan x = 2
c. koefisien  x²= 1 dan x = 5
d. koefisien x³= a ,   x²= b dan x = c

3. Soal: 2 x2 -3 + x2 – 4 = ?

Jawaban: 2 x2 -3 + x2 – 4 = (2+1) x2 + (-3-4) = 3 x2 – 7

4. Soal: 7x – 3x = ?

Jawaban: 7x – 3x = (7-3)x = 4x

5. Sederhanakan bentuk aljabar berikut:
a. 3x² – 4 x²+ 7x – 2 x + 1
b. 4x² – 2y + 1 – 5x² + x + y
c. 4 ( 2x²– y ) + 3 ( x²+ y )

Jawaban:

a. 3x² – 4 x²+ 7x – 2 x + 1
= ( 3 – 4 ) x²+ ( 7 – 2 )x + 1
= -1 x² + 5x + 1

b. 4x² – 2y + 1 – 5x² + x + y
= (4 – 5 )x² – ( 2 + 1 ) y + 1 + x
= -1x² – 3y +1 + x

c. 4 ( 2x²– y ) + 3 ( x²+ y )
= ( 4 + 3 ) + ( 2 + 1 ) x²+ ( -y + y )
= 7 + 3x²– y + y

6. Soal: 5x – 8 – 2x – 1 = ?

Jawaban: 5x – 8 – 2x – 1 = (5-2)x – (8+1) = 3x – 9

7. Soal

Faktoran seperti ini harus lebih teliti, karena jika salah taruh angka, dan min atau plus salah hasilnya akan berbeda. Caranya hampir sama yang di atas. Jika yang dikali diisi dengan konstanta, sekarang yang dikali diisi dengan konstanta kali variabel kuadrat atau angka pertama, dan ada tambahan langkahnya:

? + ? =13
? X ?=(5.6)=30
10 + 3=13
10 X 3=30
Ganti koefiesn tidak berpangkat dengan bilang yang dicari tadi
faktorkan menjadi 2, seperti faktoran contoh pertama dengan sarat dalam kurungnya sama
5x(x+2) +3(x+2}
Karena dalam kurungnya sama ambil satu kurung saaja, dan buat kurung baru untuk yang di luar
(5x+3)(x+2)

Pembuktiannya
(5x X x)+(5x X 2)+(3 X x)+(3 X 2)

Jawaban: 5x²+13x+6=(5+3)(x+2)

8. Soal:

? + ?=-8
? X ?=12

-6 + -2=-8
-6 X -2=12
Harap diingat min kali min jadi plus

3y(y-2) -2(y-2)

(3y-2)(y-2)

Pembuktiannya
(3y.y)+(3y.-2)+(-2.y)+(-2.-2)

Jawaban: 3y²-8y+4=(3y-2)(y-2)

9. Tentukan suku–suku sejenis dari pasangan berikut:
a. x² + 2x² – 1 dengan 3x² + x +xy
b. 2x²+ x dengan –x² +2
c. -2x +5 dengan 5x² -2
d. x³ – x² dengan 4x² + x

Jawaban:

a. x² + 2x – 1 dengan 3x² + x +xy
suku – suku yang sejenis adalah : x²dan 3x², 2x dan x

b. 2x²+ x dengan –x² +2
suku – suku yang sejenis adalah : 2x² dan –x²

c. -2x +5 dengan 5x² -2
suku – suku yang sejenis adalah : s dan -2

d. x³ – x² dengan 4x² + x
suku – suku yang sejenis adalah : – x²dan 4x²

10. Soal: 5x + 2 = 2x + 17

Jawaban: 5x + 2 – 2x =   2x + 17 – 2x
3x + 2   =   17
3x + 2 – 2 =   17 – 2
3x   =   15
x   =   5

11. Tentukan penjumlahan dari bentuk aljabar berikut:
a. 4x + x
b. 5xy + 6xy
c. 3xy + 3 + 4xy +1
d. ( 3x + 4xy + 2 ) + ( 3 + 4x + 2xy )

Jawaban:

a. 4x + x = 5x

b. 5xy + 6xy = 11xy

c. 3xy + 3 + 4xy +1
= ( 3 + 4 ) xy + ( 3 + 1 )
= 7xy + 4

d. ( 3x + 4xy + 2 ) + ( 3 + 4x + 2xy )
= 3x + 4xy + 2 + 3 + 4x + 2xy
= ( 3x + 4x ) + ( 4xy + 2xy ) + ( 2 + 3 )
= 7x + 6xy + 5

12. Soal: 5(x – 4) = 3x + 2

Jawaban: 5x – 20   =   3x + 2
5x – 20 – 3x =   3x + 2 – 3x
2x – 20   =   2
2x – 20 + 20 =   2 + 20
2x   =   22
x   =   11

13. Tentukan hasil pengurangan dari bentuk aljabar berikut:
a. 5xy – xy
b. 3y – 5y
c. -x – 4x

Jawaban:

a. 5xy – xy = 4 xy
b. 3y – 5y = -2y
c. -x -4x = -5x

14.Tentukan hasil dari penjumlahan dan pengurangan dari bentuk aljabar berikut:
a. -2x²+ 5x²b. ( -5 x³+ 4x²-7 ) + ( x²-x + 4 )
c. ( 3p³– 2aq² + 5 ) – ( p²– aq²-10 )
d. 3x² – 4x²+ 7x – 2x +1

Jawaban:

a. -2x²+ 5x²= ( -2 + 5 ) x²= 3 x²

b. ( -5 x³+ 4x²-7 ) + ( x²-x + 4 )
= -5 x³+ ( 4 + 1 )x²– x + ( -7 + 4 )
= -5 x³+ 5x² – x -3

c. ( 3p³– 2aq² + 5 ) – ( p²– aq²-10 )
= 3p³– p²– ( 2 – 1 ) aq²+ ( 5 – 10 )
= 3p³– p²– aq²-5

d. 3x² – 4x²+ 7x – 2x +1
= ( 3 – 4 ) x²+ ( 7 – 2 ) x + 1
= -1 x²– 5x + 1

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: CleverlySmart, Math is Fun, Teachers Choice, Interactive Mathematics, Math Planet

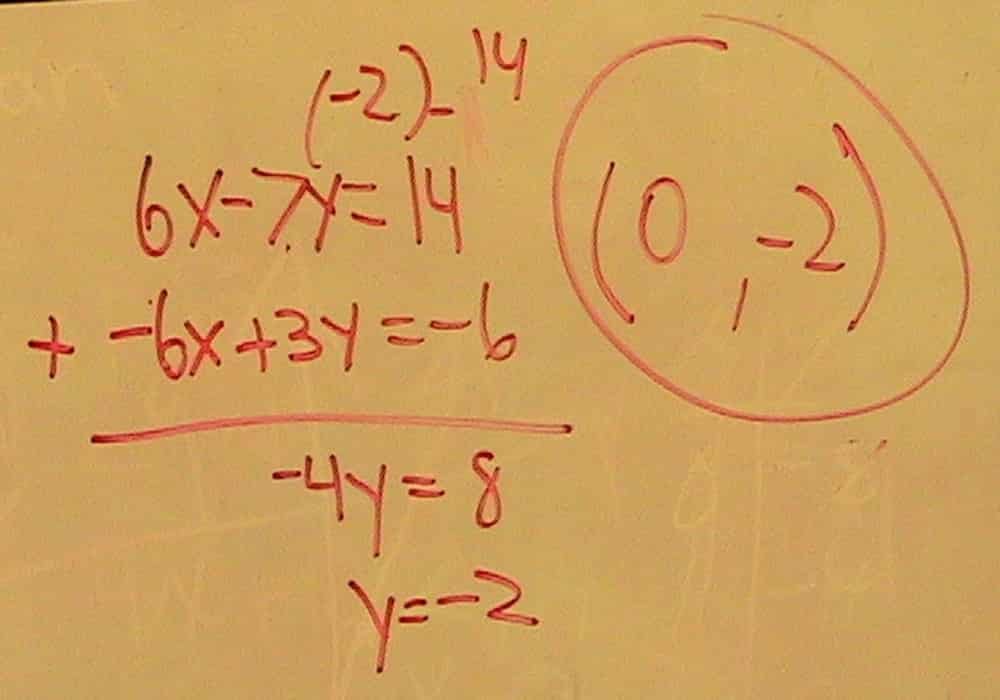
Teorema Binomial (Aljabar) | Binomial Newton

5 Replies to “Rumus Aljabar – Operasi Rumus Perhitungan, Penjelasan, Contoh Soal…”

Micheline berkata:
29/04/2018 pukul 7:30 am
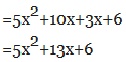
Terima kasih Pinter Pandai
1. Pinter Pandai berkata:
  30/04/2018 pukul 7:33 am
  Sama-sama Micheline 🙂
2. Pinter Pandai berkata:
  03/05/2018 pukul 8:03 am
  Sama-sama Micheline, semoga artikel ini dapat lebih membantu Anda dan banyak orang juga.
Tito berkata:
17/05/2018 pukul 3:05 pm
Bagus dan lengkap, plus ada contoh soal. Terima kasih.
1. Pinter Pandai berkata:
  18/05/2018 pukul 9:04 am
  Makasih Tito, selamat belajar!

Rumus Aljabar – Operasi Rumus Perhitungan, Penjelasan, Contoh Soal dan Jawaban

Penjumlahan dan Pengurangan Bentuk Aljabar

Rumus Penjumlahan Bentuk Aljabar

Rumus Pengurangan Bentuk Aljabar

Penjelasan Aljabar

Rumus kuadrat aljabar:

Operasi bentuk aljabar

Istilah – istilah yang perlu di pahami dalam bentuk aljabar

Aljabar elementer

Polinomial

Aljabar abstrak

Himpunan

Operasi biner

Elemen identitas

Elemen invers atau unsur balikan

Asosiativitas

Komutativitas

Grup

Bilangan rasional tak-nol membentuk grup di bawah operasi perkalian.

Gelanggang dan medan

Unsur pada Bentuk Aljabar

Variabel, Konstanta, Koefisien & Faktor

Suku Sejenis dan Suku Tak Sejenis

Suku Satu, Suku Dua, Suku Tiga dan Suku Banyak

Operasi Perhitungan pada Bentuk Aljabar

Operasi Penjumlahan dan Pengurangan

Operasi Perkalian pada Bentuk Aljabar

Operasi Perpangkatan dalam Bentuk Aljabar

PENGERTIAN BILANGAN BERPANGKAT

SIFAT – SIFAT BILANGAN DENGAN PANGKAT

Operasi Pembagian dalam Bentuk Aljabar

Contoh Soal Aljabar dan Jawaban

1. Soal: 7x + 3x = ?

2. Tentukan koefisien dari bentuk – bentuk aljabar berikut: a. 2x2 + x – 1 b. 3x2 +- 2x + 1 c. x2 + 5x – 6 d. ax3 + bx2 + cx + d

3. Soal: 2 x2 -3 + x2 – 4 = ?

4. Soal: 7x – 3x = ?

5. Sederhanakan bentuk aljabar berikut: a. 3x2 – 4 x2 + 7x – 2 x + 1 b. 4x2 – 2y + 1 – 5x2 + x + y c. 4 ( 2x2 – y ) + 3 ( x2 + y )

6. Soal: 5x – 8 – 2x – 1 = ?

7. Soal <img decoding="async" src="https://1.bp.blogspot.com/-SqP3IXLVDuo/WM7_afuj0uI/AAAAAAAAAN4/qEqHlPBBWuUYxS5naTaVPuMRDnlWpqsRACLcB/s1600/pemfaktoran.jpg" border="0" />

8. Soal: <img decoding="async" src="https://1.bp.blogspot.com/-C0lqLJ6Byxk/WM8ArHoU9mI/AAAAAAAAAOI/RdzGB-Qcxgk_96QX3MtLkyxahv1wnRy5ACLcB/s1600/pemfaktoran4.jpg" border="0" />

9. Tentukan suku–suku sejenis dari pasangan berikut: a. x2 + 2x2 – 1 dengan 3x2 + x +xy b. 2x2 + x dengan –x2 +2 c. -2x +5 dengan 5x2 -2 d. x3 – x2 dengan 4x2 + x

10. Soal: 5x + 2 = 2x + 17

11. Tentukan penjumlahan dari bentuk aljabar berikut: a. 4x + x b. 5xy + 6xy c. 3xy + 3 + 4xy +1 d. ( 3x + 4xy + 2 ) + ( 3 + 4x + 2xy )

12. Soal: 5(x – 4) = 3x + 2

13. Tentukan hasil pengurangan dari bentuk aljabar berikut: a. 5xy – xy b. 3y – 5y c. -x – 4x

14.Tentukan hasil dari penjumlahan dan pengurangan dari bentuk aljabar berikut: a. -2x2 + 5x2 b. ( -5 x3 + 4x2 -7 ) + ( x2 -x + 4 ) c. ( 3p3 – 2aq2 + 5 ) – ( p2 – aq2 -10 ) d. 3x2 – 4x2 + 7x – 2x +1

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

5 Replies to “Rumus Aljabar – Operasi Rumus Perhitungan, Penjelasan, Contoh Soal…”

Tinggalkan Balasan Batalkan balasan

2. Tentukan koefisien dari bentuk – bentuk aljabar berikut:
a. 2x² + x – 1
b. 3x² +- 2x + 1
c. x² + 5x – 6
d. ax³+ bx² + cx + d

5. Sederhanakan bentuk aljabar berikut:
a. 3x² – 4 x²+ 7x – 2 x + 1
b. 4x² – 2y + 1 – 5x² + x + y
c. 4 ( 2x²– y ) + 3 ( x²+ y )

7. Soal

8. Soal:

9. Tentukan suku–suku sejenis dari pasangan berikut:
a. x² + 2x² – 1 dengan 3x² + x +xy
b. 2x²+ x dengan –x² +2
c. -2x +5 dengan 5x² -2
d. x³ – x² dengan 4x² + x

11. Tentukan penjumlahan dari bentuk aljabar berikut:
a. 4x + x
b. 5xy + 6xy
c. 3xy + 3 + 4xy +1
d. ( 3x + 4xy + 2 ) + ( 3 + 4x + 2xy )

13. Tentukan hasil pengurangan dari bentuk aljabar berikut:
a. 5xy – xy
b. 3y – 5y
c. -x – 4x

14.Tentukan hasil dari penjumlahan dan pengurangan dari bentuk aljabar berikut:
a. -2x²+ 5x²b. ( -5 x³+ 4x²-7 ) + ( x²-x + 4 )
c. ( 3p³– 2aq² + 5 ) – ( p²– aq²-10 )
d. 3x² – 4x²+ 7x – 2x +1