Teori Relativitas Khusus
Teori relativitas khusus menjelaskan bagaimana ruang dan waktu terhubung untuk objek yang bergerak pada kecepatan yang konsisten dalam garis lurus. Salah satu aspek yang paling terkenal adalah benda bergerak dengan kecepatan cahaya.
Teori relativitas khusus Einstein berlandaskan pada dua prinsip:
- Prinsip relativitas : Hukum fisika tidak berubah untuk semua objek yang bergerak kerangka acuan inersial (kecepatan tetap).
- Prinsip kecepatan cahaya : Kecepatan cahaya adalah sama untuk semua pengamat, tidak bergantung pada kecepatan gerak pengamat relatif terhadap sumber cahaya.
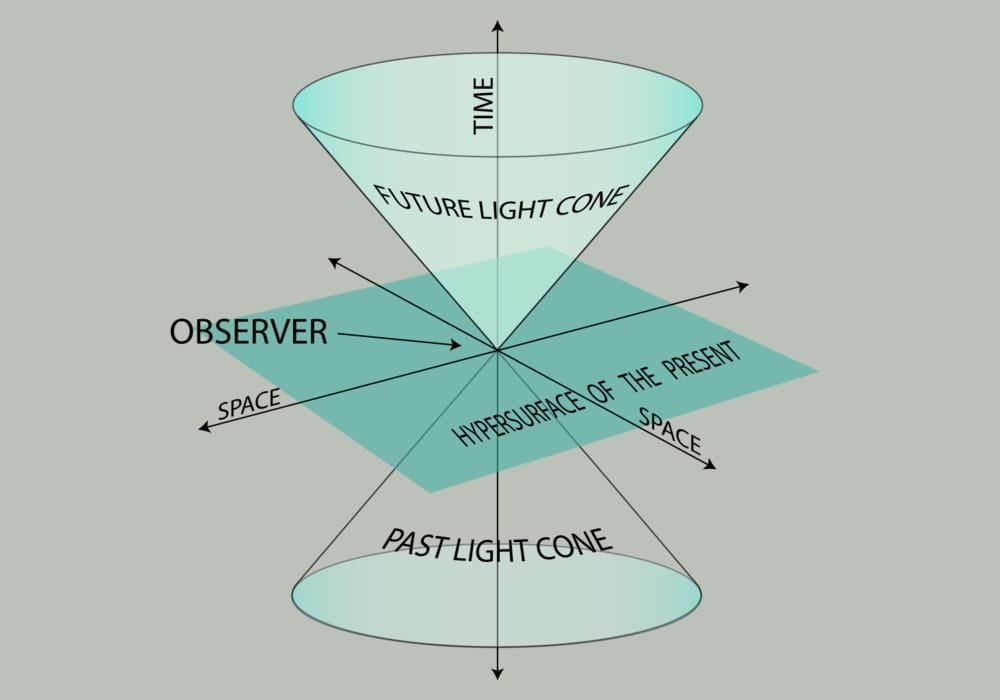
Teori relativitas khusus Einstein menciptakan hubungan fundamental antara ruang dan waktu.
Alam semesta dapat dipandang memiliki tiga dimeni ruang dansatu dimensi waktu. Empat deimensi ini diebut kontinum ruang-waktu.
Sederhananya, ketika sebuah objek mendekati kecepatan cahaya, massanya menjadi tak terhingga dan ia tidak dapat bergerak lebih cepat daripada perjalanan cahaya. Batas kecepatan kosmik ini telah menjadi pokok bahasan banyak diskusi dalam fisika, dan bahkan dalam fiksi ilmiah, ketika orang berpikir tentang bagaimana melakukan perjalanan melintasi jarak yang sangat jauh.
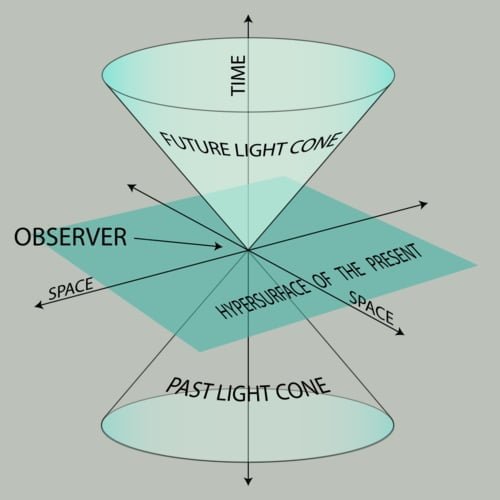
SVG version: K. Aainsqatsi at en.wikipedia
Original PNG version: Stib at en.wikipedia
Pembuktian relativitas khusus
Dua postulat (tesis atau disertasi) relativitas khusus adalah sebagai berikut: Hukum fisika memiliki bentuk yang sama di semua kerangka acuan Galilea. Kecepatan cahaya dalam ruang hampa memiliki nilai yang sama di semua kerangka acuan Galilea.
Baca juga: Kecepatan Cahaya Nilai Presisinya adalah 299792458 Meter per Detik
Teori relativitas khusus dikembangkan oleh Albert Einstein pada tahun 1905 dan membentuk bagian dari dasar fisika modern
Setelah menyelesaikan karyanya dalam relativitas khusus, Einstein menghabiskan satu dekade merenungkan apa yang akan terjadi jika seseorang memperkenalkan akselerasi. Ini membentuk dasar dari relativitas umum, yang diterbitkan pada tahun 1915.
- Kecepatan relatif
- Dilatasi waktu (termasuk “paradok kembar” yang terkenal)
- Konstraksi panjang (konstraksi Lorentz)
- Massa relativistik
- Energi kinetik relativistik
- Energi total relativistik
- Momentum relativistik
- Efek Doppler relativistk
- Simultanitas dan sinkronisasi waktu
Dilatasi Waktu
Dilatasi waktu adalah konsekuensi dari teori relativitas khusus di mana dua pengamat yang bergerak relatif terhadap satu sama lain akan mengamati bahwa jam pengamat lain berdetak lebih lambat dari jamnya. Peristiwa ini bukanlah akibat dari kesalahan jam atau faktor teknis lainnya, tetapi merupakan sifat dasar dari ruang-waktu yang dijelaskan dalam teori relativitas.
Kebingungan yang sering muncul dalam mempelajari efek ini adalah efek ini berlaku dua arah: jika pengamat A mengamati bahwa jam pengamat B berdetak lebih lambat karena efek ini, maka pengamat B juga akan mengamati bahwa jam pengamat A berdetak lebih lambat. Hal ini sangat berlawanan dengan intuisi: jika A mengamati jam B berdetak lebih lambat maka B akan mengamati jam A berdetak lebih cepat.
Secara kuantitatif, jika menurut pengamat A jamnya menyatakan selang waktu sebesar 

di mana 

Konstraksi panjang (konstraksi Lorentz)
Bentuk transformasi yang paling umum dinyatakan sebagai
yang dimana (t, x, y, z) and (t′, x′, y′, z′) mewakili suatu koordinat peristiwa dalam dua frame dengan kecepatan relatif v, c adalah kecepatan cahaya, dan
Pengantar relativitas umum
Pada awal abad ke-20, hukum-hukum Newton tentang gravitasi universal telah diterima selama lebih dari dua ratus tahun sebagai penjelasan valid dari gaya gravitasi antar massa. Dalam model Newton, gravitasi adalah hasil dari kekuatan tarik antara benda-benda besar. Meskipun bahkan Newton bermasalah dengan sifat alami gaya tersebut yang tidak diketahui, kerangka dasar ini sangat sukses dalam menggambarkan gerak.
Percobaan dan pengamatan menunjukkan bahwa deskripsi Einstein mengenai gravitasi memperhitungan beberapa efek yang tidak dapat dijelaskan oleh hukum Newton, seperti anomali menit dalam orbit dari Merkurius dan planet-planet lainnya. Relativitas umum juga memprediksi efek novel gravitasi, seperti gelombang gravitasi, lensa gravitasidan efek gravitasi pada waktu yang dikenal sebagai dilatasi waktu gravitasi. Banyak dari prediksi ini telah dikonfirmasi oleh percobaan atau pengamatan, yang paling baru adalah gelombang gravitasi.
Relativitas umum telah berkembang menjadi alat penting dalam astrofisika modern
Teori ini memberikan dasar untuk pemahaman lubang hitam, daerah ruang di mana efek gravitasi begitu kuat sehingga bahkan cahaya tidak dapat lolos. Gravitasi yang begitu kuat dianggap menjadi penyebab atas radiasi intensi yang dipancarkan oleh beberapa tipe objek astronomi (seperti inti galaksi aktif atau mikrokuasar). Relativitas umum juga merupakan bagian dari kerangka standar model kosmologi Ledakan Dahsyat.
Meskipun relativitas umum bukan hanya teori relativistik satu-satunya, teori ini adalah teori paling sederhana yang konsisten dengan data eksperimen. Namun demikian, sejumlah pertanyaan tetap terbuka, yang paling mendasar adalah bagaimana relativitas umum dapat digabungkan dengan hukum fisika kuantum untuk menghasilkan teori gravitasi kuantum yang lengkap dan konsisten.
Dari relativitas khusus ke relativitas umum
Pada bulan September 1905, Albert Einstein menerbitkan teorinya mengenai relativitas khusus, yang menggabungkan hukum Newton tentang gerak dengan elektrodinamika (interaksi antara benda dengan muatan listrik). Relativitas khusus memperkenalkan kerangka kerja baru untuk ilmu fisika dengan mengusulkan konsep-konsep baru tentang ruang dan waktu.
Beberapa teori fisika yang kemudian diterima inkonsisten dengan kerangka itu; contohnya adalah teori Newton tentang gravitasi, yang menggambarkan saling tarik yang dialami oleh tubuh karena massa mereka.
Beberapa fisikawan, termasuk Einstein, mencari sebuah teori yang dapat menggabungkan hukum gravitasi Newton dan relativitas khusus. Hanya teori Einstein terbukti konsisten dengan eksperimen dan pengamatan. Untuk memahami ide-ide dasar teori, maka mengikuti pikiran Einstein antara 1907 dan 1915, dari yang eksperimen pemikiran sederhana yang melibatkan pengamat jatuh bebas ke teori gravitasi geometriknya.[1]
Prinsip yang setara
Seseorang dalam elevator yang jatuh bebas akan mengalami kehilangan bobot; benda melayang tak bergerak atau melayang pada kecepatan konstan. Karena segala sesuatu di lift jatuh bersama-sama, tidak ada efek gravitasi dapat diamati. Dengan cara ini, pengalaman dari seorang pengamat yang jatuh bebas tidak dapat dibedakan dari orang-orang dari pengamat di luar angkasa, jauh dari sumber gravitasi yang signifikan. Pengamat tersebut adalah yang diistimewakan (“inersia”) yang dijelaskan Einstein dalam teorinya relativitas khusus: pengamat untuk siapa cahaya bergerak sepanjang garis lurus dengan kecepatan konstan.
Secara kasar, prinsip ini menyatakan bahwa seseorang dalam lift yang jatuh bebas tidak bisa mengatakan bahwa mereka sedang jatuh bebas. Setiap percobaan dalam keadaan lingkungan jatuh bebas memiliki hasil yang sama. Seperti pengamat pada saat diam atau bergerak di angkasa secara seragam, jauh dari semua sumber gravitasi.
Gravitasi dan percepatan
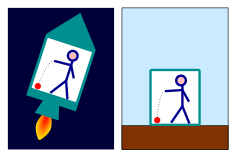
Sebagian besar efek gravitasi hilang pada jatuh bebas, tetapi efek yang terlihat sama seperti gravitasi tersebut dapat diproduksi oleh kerangka acuan yang dipercepat. Seorang pengamat di sebuah ruangan tertutup tidak bisa mengatakan yang mana dari berikut ini benar:
- Benda-benda yang jatuh ke lantai karena ruangan sedang diam di permukaan Bumi dan objek yang ditarik ke bawah oleh gravitasi.
- Benda-benda yang jatuh ke lantai karena ruangan berada di atas roket luar angkasa, yang dipercepat pada 9.81 m/s2 dan jauh dari sumber gravitasi. Benda-benda yang ditarik menuju lantai sama seperti “gaya inersia” yang menekan pengemudi ke belakang pada mobil yang dipercepat.
Sebaliknya, efek teramati pada kerangka acuan yang dipercepat juga harus diamati dalam medan gravitasi dengan kekuatan yang setara. Prinsip ini memungkinkan Einstein untuk memprediksi beberapa efek novel gravitasi pada tahun 1907, seperti yang dijelaskan dalam bagian berikutnya.
Relativitas umum
Prediksi relativitas umum yang berbeda
Banyak prediksi relativitas umum yang berbeda dengan prediksi fisika klasik, utamanya prediksi mengenai berjalannya waktu, geometri ruang, gerak benda pada jatuh bebas, dan perambatan cahaya. Contoh perbedaan ini meliputi dilasi waktu gravitasional, geseran merah gravitasional cahaya, dan tunda waktu gravitasional. Prediksi-prediksi relativitas umum telah dikonfirmasikan dalam semua percobaan dan pengamatan fisika. Walaupun relativitas umum bukanlah satu-satunya teori relativistik gravitasi, ia merupakan teori paling sederhana yang konsisten dengan data eksperimen.
Namun, masih terdapat banyak pertanyaan yang belum terjawab. Secara mendasar, terdapat pertanyaan bagaimanakah relativitas umum ini dapat digabungkan dengan hukum-hukum fisika kuantum untuk menciptakan teori gravitasi kuantumyang lengkap dan swa-konsisten.
Teori Einstein memiliki implikasi astrofisika yang penting
Teori ini memprediksikan adanya keberadaan daerah lubang hitam yang mana ruang dan waktu terdistorsi sedemikiannya tiada satu pun, bahkan cahaya pun, tidak dapat lolos darinya. Terdapat bukti bahwa lubang hitam bintang dan jenis-jenis lubang hitam lainnya yang lebih besar bertanggung jawab terhadap radiasi kuat yang dipancarkan oleh objek-objek astronomi tertentu, seperti inti galaksi aktif dan mikrokuasar. Melengkungnya cahaya oleh gravitasi dapat menyebabkan fenomena pelensaan gravitasi.
Relativitas umum juga memprediksikan keberadaan gelombang gravitasi. Keberadaan gelombang ini telah diukur secara tidak langsung, dan terdapat pula beberapa usaha yang dilakukan untuk mengukurnya secara langsung.
Selain itu, relativitas umum adalah dasar dari model kosmologis untuk alam semesta yang terus berkembang.
Relativitas umum menjadi penting ketika kita memandang sebuah sistem dengan jari-jari jauh lebih kecil daripada massa atau pun massa jauh lebih besar daripada jari-jari. Kasus pertama berlaku pada objek-objek yang mengalami keruntuhan gravitasi seperti bintang neutron atau sebuah lubang hitam yang memiliki massa sebanding dengan massa sebuah bintang (meskipun ada juga lubang hitam yang lebih besar) tetapi dengan radius yang kecil.
Kasus kedua berlaku pada kosmologi, yakni jika ruang diisi dengan materi dengan kerapatan yang sama dimana-mana, maka jika kita mencuplik ruang tersebut dengan jari-jari yang makin besar dan terus membesar, massa akan bertambah dengan laju yang sebanding dengan R3.
Sejarah Teori Relativitas Albert Einstein
Segera setelah mempublikasikan teori relativitas khusus tahun 1905, Einstein mulai berpikir bagaimana menggabungkan gravitasi ke dalam kerangka kerja relativistiknya yang baru.
Pada tahun 1907, percobaan sederhana dengan pengamatan jatuh bebas memulai pengamatannya selama 8 tahun berikutnya dalam teori gravitasi relativistik.
Setelah berulang kali memperbaiki kesalahan, ia mengumumkan hasil kerjanya ke Akademi Sains Prusia pada bulan November 1915 dan menjadi apa yang kita kenal sekarang sebagai persamaan medan Einstein.
Persamaan ini menunjukkan bagaimana geometri ruang dan waktu dipengaruhi kehadiran materi dan radiasi dan membentuk inti dari teori relativitas umum Einstein.
Persamaan medan Einstein nonlinear dan sangat sulit diselesaikan. Einstein menggunakan metode pendekatan dalam mengerjakan prediksi awal teori tersebut. Pada tahun 1916, astrofisikawan Karl Schwarzschild menemukan persamaan eksak untuk persamaan medan Einstein yang kemudian dikenal sebagai metrik Schwarzschild.
Solusi ini memberikan dasar bagi penjelasan tahap akhir hilangnya gravitasi, dan objek yang kita kenal saat ini sebagai lubang hitam. Pada tahun yang sama, dilakukan langkah untuk menggeneralisasi penyelesaian Schwarzschild terhadap benda bermuatan listrik, yang kemudian dihasilkan penyelesaian Reissner–Nordström, saat ini dihubungkan dengan lubang hitam bermuatan listrik.
Relativitas umum dapat dipahami dengan baik dengan mengevaluasi kemiripannya beserta perbedaannya dari fisika klasik. Langkah pertama adalah realisasi bahwa mekanika klasik dan hukum gravitasi Newton mengizinkan adanya deskripsi geometri.
Kombinasi deskripsi ini dengan hukum-hukum relativitas khusus akan membawa kita kepada penurunan heuristik relativitas umum.
Geometri gravitasi Newton
Dasar dari mekanika klasik adalah gagasan bahwa gerak benda dapat dideskripsikan sebagai kombinasi gerak bebas (atau gerak inersia) dengan penyimpangan dari gerak bebas ini.
Penyimpangan ini disebabkan oleh gaya-gaya luar yang bekerja pada benda sesuai dengan hukum kedua Newton, yang menyatakan bahwa total keseluruhan gaya yang bekerja pada sebuah benda adalah sama dengan massa (inersia) benda tersebut dikalikan dengan percepatannya.
Gerak inersia yang dihasilkan berhubungan dengan geometri ruang dan waktu, yakni dalam standar kerangka acuan mekanika klasik, benda yang berada dalam keadaan jatuh bebas bergerak searah garis lurus dengan kecepatan konstan.
Dalam bahasa fisika modern, lintasan benda bersifat geodesik, yaitu garis dunia yang lurus dalam ruang waktu.
Sebaliknya, seseorang dapat mengharapkan bahwa seketika berhasil diidentifikasi dengan memantau gerak benda sebenarnya dan mempertimbangkan gaya-gaya luar (seperti gaya elektromagnetik dan gesekan), gerak inersia dapat digunakan untuk menentukan geometri ruang dan juga waktu. Namun, akan terdapat ambiguitas ketika gravitasi diperhitungkan ke dalamnya.
Menurut hukum gravitasi Newton, terdapat apa yang disebut sebagai universalitas jatuh bebas, yaitu bahwa lintasan suatu benda yang jatuh bebas bergantung hanya pada posisi dan kecepatan awalnya, dan bukannya bergantung pada sifat-sifat bahan penyusunnya.
Versi yang lebih sederhana dapat dilihat pada percobaan elevator Einstein, yang digambarkan pada gambar di samping. Untuk seorang pengamat dalam ruang tertutup yang kecil, adalah tidak mungkin untuk menentukan apakah ruang itu berada dalam keadaan diam dalam suatu medan gravitasi; ataukah ia berada di dalam roket yang dipercepat hanya dengan memetakan lintasan bola jatuh tersebut.
Universalitas jatuh bebas
Disebabkan oleh universalitas jatuh bebas, tiada perbedaan terpantau yang dapat dipantau antara gerak inersial dengan gerak yang berada di bawah pengaruh gaya gravitasi.
Ini kemudian mengarahkan kita pada suatu definisi gerak inersia yang baru; yaitu gerak inersia objek jatuh bebas yang berada di bawah pengaruh gaya gravitasi. Jenis gerak ini juga menentukan geometri ruang dan waktu.
Gerak ini adalah gerak geodesik yang diasosiasikan dengan koneksi tertentu yang bergantung pada gradienpotensial gravitasi.
Ruang, dalam konstruksi ini, masih memiliki geometri Euklides yang seperti biasanya, namun ruang waktu secara keseluruhan menjadi lebih rumit. Seperti yang dapat ditunjukkan dengan menggunakan eksperimen pemikiran sederhana yang menelusuri lintasan partikel-partikel pengujian yang sedang jatuh bebas; hasil dari pemasukan vektor-vektor ruang waktu yang menandakan kecepatan suatu partikel akan bervariasi sesuai dengan lintasan partikel.
Secara matematis, kita katakan bahwa koneksi Newton tidaklah terintegralkan.
Dari hal ini, seseorang dapat mendeduksi bahwa ruang waktu adalah melengkung. Akibatnya adalah perumusan geometri gravitasi Newton yang hanya menggunakan konsep kovarian. Dalam deskripsi geometri ini, efek pasang surut – yaitu percepatan relatif benda yang jatuh bebas – berhubungan dengan turunan koneksi, menunjukkan bagaiman geometri yang dimodifikasikan ini diakibatkan oleh keberadaan massa.
Generalisasi relativistik
Geometri gravitasi Newton pada dasarnya didasarkan pada mekanika klasik. Ia hanyalah kasus khusus dari mekanika relativitas khusus. Dalam bahasa simetri: ketika gravitasi dapat diabaikan, fisika yang berlaku bersifat invarian Lorentz pada relativitas khusus daripada invarian Galileo pada mekanika klasik.
Perbedaan antara keduanya menjadi signifikan apabila kecepatan terlibat di dalamnya mendekati kecepatan cahaya dan berenergi tinggi.
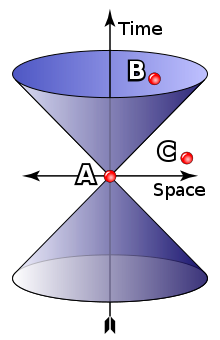
Menggunakan simetri Lorentz, struktur-struktur tambahan mulai berperan penting. Struktur-struktur tambahan ini dijelaskan menggunakan sekumpulan kerucut cahaya. Kerucut cahaya mendefinisikan struktur sebab-akibat:
- untuk setiap peristiwa A, terdapat sekumpulan peristiwa yang menurut prinsipnya dapat memengaruhi ataupun dipengaruhi oleh A melalui sinyal maupun interaksi yang tidak seperlunya merambat lebih cepat daripada cahaya (misalnya pada peristiwa B pada gambar)
- beserta sekumpulan peristiwa yang tidak memungkinkan memperngaruhi atau dipengaruhi oleh A (seperti pada peristiwa C pada gambar).
Sekumplan peristiwa ini tak bergantung pada pengamat. Bersamaan dengan garis dunia partikel jatuh bebas, kerucut cahaya dapat digunakan untuk merekonstruksi metrik semi-Riemann ruang waktu.
Relativitas khusus
dideskripsikan tanpa keberadaan percepatan, sehingganya ia hanya cocok dijadikan sebagai model fisika di mana percepatan dapat di abaikan, dalam hal ini percepatan gravitasi.
Ketika gravitasi terlibat di dalamnya, dengan berasumsi pada universalitas jatuh bebas, maka tiada kerangka inersia global apapun. Yang ada adalah kerangka inersia hampiran yang bergerak sepanjang partikel yang jatuh bebas.
Menggunakan bahasa ruang waktu: garis lurus bak-waktu yang menentukan kerangka inersial tanpa gravitasi dideformasi menjadi garis yang melengkung relatif terhadap satu sama lainnya. Hal ini mensugestikan bahwa pemasukan gravitasi memerlukan perubahan pada geometri ruang waktu.
Kerangka lokal baru dalam peristiwa jatuh bebas
Secara a apriori, tidaklah jelas apakah kerangka lokal baru dalam peristiwa jatuh bebas bertepatan dengan kerangka acuan di mana hukum-hukum relativitas khusus berlaku. Teori relativitas khusus didasarkan pada perambatan cahaya (sehingganya berkaitan dengan elektromagnetisme) dan dapat memiliki sekumpulan kerangka acuan yang berbeda.
Namun menggunakan bermacam-macam asumsi mengenai kerangka relativitas khusus (misalnya dalam keadaan jatuh bebas), kita dapat menurunkan prediksi yang berbeda mengenai geseran merah gravitasional, yakni bagaimana frekuensi cahaya dapat bergeser seiring dengan merambatnya cahaya melalui medan gravitasi.
Berdasarkan hasil pengukuran aktual, kerangka acuan jatuh bebas tersebut adalah kerangka yang mana cahaya merambat sebagaimana yang ada dalam teori relativitas khusus.
Generalisasi pernyataan bahwa hukum-hukum relativitas khusus berlaku sebagai pendekatan yang cukup baik dalam kerangka acuan yang sedang jatuh bebas (dan tidak berotasi); dikenal sebagai Prinsip kesetaraan Einstein. Prinsip ini sangat krusial dalam pengeneralisasian hukum-hukum fisika relativitas khusus agar gravitasi dapat dilibatkan.
Hasil data percobaan
Hasil data percobaan yang sama juga menunjukkan bahwa waktu yang diukur oleh jam yang berada dalam medan gravitasi (waktu wajar) tidak mengikuti hukum-hukum relativitas khusus.
Dalam bahasa geometri ruang-waktu, waktu wajar tidak terukur oleh metrik Minkowski. Dalam skala kecil, semua kerangka acuan yang berada dalam keadaan jatuh bebas adalah setara dan mendekati metrik Minkowski.
Tensor metrik yang menentukan geometri, yakni bagaimana panjang dan sudut ukur, bukanlah metrik Minkowski relativitas khusus, melainkan generalisasi yang dikenal sebagai metrik semi- atau pseudo-Riemann.
Lebih jauh lagi, tiap-tiap metrik Riemann secara alaminya memiliki satu jenis koneksi khusus, yaitu koneksi Levi-Civita. Koneksi inilah yang memenuhi prinsip kesetaraan dan membuat ruang secara lokal bermetrik Minkowski.
Contoh Soal dan Jawaban Relativitas Khusus
Jika sebuah kereta api bergerak dengan kecepatan 120 km/jam. Seekor burung yang hinggap di atas kereta terbang dengan kecepatan 5 km/jam searah kereta tersebut.
Berapa kecepatan terbang burung tersebut tersebut menurut seseorang yang berada di dalam kereta api dan menurut orang yang sedang berdiri di stasiun?
Jawaban:
a. Kecepatan burung relatif terhadap kereta api adalah v’x = 5 km/jam
b. Kecepatan burung relatif terhadap stasiun adalah
vx = v + v’x
= 120 + 5 = 125 km/jam
Bacaan Lainnya
- Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang
- Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender
- Cara Menghentikan Penindasan Bullying
- Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
- Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
- 10 Cara Memotivasi Anak Untuk Belajar Agar Menjadi Pintar
- Di Indonesia, (HAN) Hari Anak Nasional tanggal 23 Juli
- Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
- Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: CleverlySmart (Special Relativity Theory), CleverlySmart (General Relativity Theory)
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing