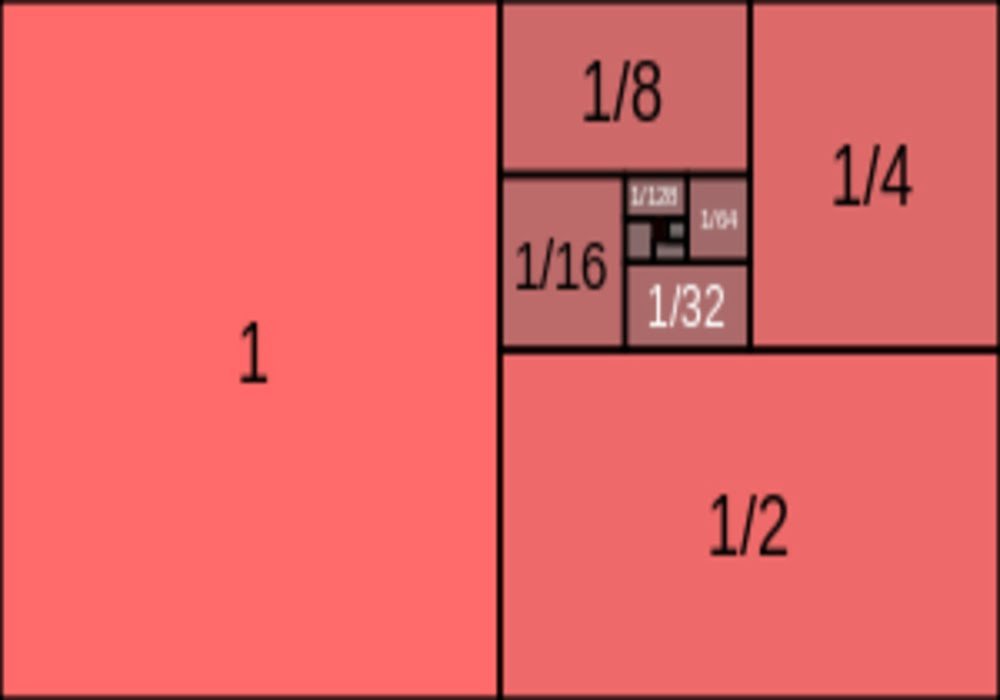
Deret Ukur atau Deret Geometri

Deret ukur atau deret geometri dalam bidang matematika adalah urutan bilangan di mana bilangan berikutnya merupakan perkalian dari bilangan sebelumnya dengan suatu bilangan rasio tertentu. Deret ukur dapat dinyatakan dengan rumus sebagai berikut:

ar^{0}=a,ar^{1}=ar,ar^{2},ar^{3},...\,

di mana r ≠ 0 adalah bilangan rasio pengali dan a adalah faktor skala. Dalam hal ini suku ke-n:

a_{n}=a\,r^{n-1}

Jumlah semua suku:

\sum _{k=0}^{n-1}ar^{k}={\frac {a(r^{n}-1)}{r-1}}

untuk r > 1, dan

$\sum _{k=0}^{n-1}ar^{k}={\frac {a(1-r^{n})}{1-r}}$ untuk r < 1.

1. Pembuktian deret geometri

Suku ke-n: $a_{1}=a$; $a_{2}=a\,r^{1}$; $a_{3}=a\,r^{2}$

….

a_{n}=a\,r^{n-1}

jadi jumlah suku ke-n adalah $a_{n}=a\,r^{n-1}$

Jumlah suku ke-n: $s_{n}=a+a\,r^{1}+a\,r^{2}+....+a\,r^{n-2}+a\,r^{n-1}$ …. (1); $s_{n}r=a\,r^{1}+a\,r^{2}+a\,r^{3}+....+a\,r^{n-1}+a\,r^{n}$ … (2) dikalikan dengan r

persamaan (1) dikurangi (2) menjadi:

s_{n}-s_{n}r=a-a\,r^{1}+a\,r^{1}-a\,r^{2}+a\,r^{2}-a\,r^{3}+....+a\,r^{n-2}-a\,r^{n-1}+a\,r^{n-1}-a\,r^{n}

s_{n}\,(1-r)=a-a\,r^{n}

s_{n}={\frac {a\,(1-r^{n})}{1-r}}

2. Deret geometri tak terhingga

s_{\infty }={\frac {a}{1-r}}

untuk -1 < r < 1 di mana

n

adalah

\infty

serta

r^{n}

adalah 0.

3. Ganjil dan genap

s_{n}={\frac {a}{1-r^{2}}}

untuk bilangan ganjil.

s_{n}={\frac {a\,r}{1-r^{2}}}

untuk bilangan genap.

Rumus umum deret geometri

a_{n}=a\,r^{n-1}

s_{n}={\frac {a\,(1-r^{n})}{1-r}}

untuk r < 1

s_{n}={\frac {a\,(r^{n}-1)}{r-1}}

untuk r > 1

s_{\infty }={\frac {a}{1-r}}

untuk -1 < r < 1

r={\frac {a_{n}}{a_{n-1}}}

u_{t}={\sqrt {a\,{a_{n}}}}

n_{b}=n+(n-1)x

r_{b}=r^{\frac {1}{x+1}}

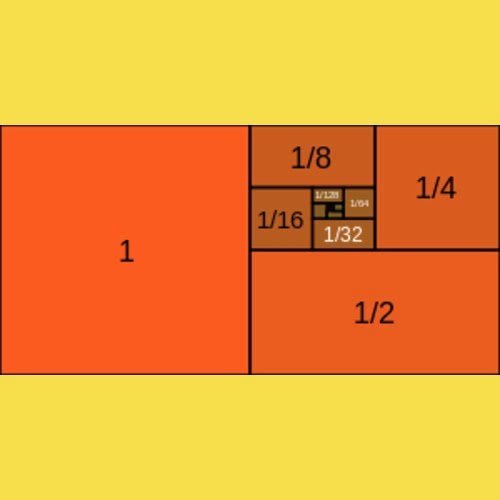
Deret geometri deret ukur — Diagram yang menunjukkan jumlah 1 + 1/2 + 1/4 + 1/8 + … adalah mendekati 2.

Soal dan Jawaban Deret Geometri

1. Soal: $\displaystyle \int \left( \sin x + \sin^3 x + \sin^5 + \dots \right) \, \mathrm{d}x = ...$

Jawaban:

Bentuk dalam integral merupakan Deret Geometri tak hingga dengan suku pertama $a = \sin x$ dan rasio $r = \sin^2 x$ , sehingga bentuk integral tersebut dapat ditulis

$\displaystyle \begin{aligned} \int \left( \sin x + \sin^3 x + \sin^5 + \dots \right) \, \mathrm{d}x &= \int \dfrac{\sin x}{1-\sin^2 x} \, \mathrm{d}x \end{aligned}$

Dengan memisalkan $u = \cos x \rightarrow -\mathrm{d}u = \sin x \, \mathrm{d}x$ dan mengganti $1 - \sin^2 x = \cos^2 x = u^2$ maka

$\displaystyle \begin{aligned} \int \dfrac{\sin x}{1-\sin^2 x} \, \mathrm{d}x &= \int \dfrac{1}{u^2} \, (-\mathrm{d}u) \\ &= u^{-1} + C \\ &= \sec x + C \\ \end{aligned}$

2. Soal: Diketahui deret yang tak hingga $~u_1+u_2+u_3+\dots$ , Jika rasio deret tersebut adalah $~r~$ dengan $~-1<r<1$ ,
$u_1+u_2+u_3+\dots=3$ , dan
$u_3+u_4+u_5+\dots=1$ , maka nilai $~r~$ adalah…

Jawaban:

$~-1<r<1 \rightarrow \text{ deret geometri konvergen }$ .

$u_1+u_2+u_3+\dots=3$

$\displaystyle \begin{aligned} S_\infty&=\frac{a}{1-r}\\ 3&=\frac{a}{1-r}~~~~~... (1) \end{aligned}$

$u_3+u_4+u_5+\dots=1$

$\displaystyle \begin{aligned} S_\infty&=\frac{ar^2}{1-r}\\ 1&=\frac{ar^2}{1-r}~~~~~... (2) \end{aligned}$

Dengan membagi pers (2) oleh (1) diperoleh

$\displaystyle \begin{aligned} r^2&=\frac{1}{3} \\ \therefore\: r&=\pm \frac{1}{\sqrt{3}} \end{aligned}$

catatan:
Deret yang tak hingga konvergen
$\boxed{~S_\infty=\frac{a}{1-r}~}$

Suku ke-n barisan geometri
$\boxed{~U_n=ar^{r-1}~}$

3. Soal: Tiga bilangan membentk barisan geometri dengan rasio positif. Jika bilangan kedua ditambah 4, diperoleh barisan aritmetika. Jika bilangan pertama adalah 2, maka jumlah ketiga bilangan semula adalah…

Jawaban:

$\displaystyle \begin{array}{cccl} 2,&2r,&2r^2& ~\text{ (Barisan Geometri)}\\ 2,&2r+4,&2r^2& ~\text{ (Barisan Aritmetika)} \end{array}$

Pada barisan aritmetika dengan menggunakan rumus suku tengah diperoleh:

$\displaystyle \begin{aligned} 2(2r+4)&=a+2r^2\\ r^2-2r-3&=0\\ (r-3)(r+1)&=0\\ \therefore\: r_1&=3\\ r_2&=-1&~~~~\text{(tidak memenuhi, r harus positif)} \end{aligned}$

Jadi jumlah 3 suku pertamanya: $2+2(3)+2(3)^2=26$