Deret Taylor

Dalam matematika Deret Taylor adalah representasi fungsi matematika sebagai jumlahan tak hingga dari suku-suku yang nilainya dihitung dari turunan fungsi tersebut di suatu titik. Deret ini dapat dianggap sebagai limit polinomial Taylor. Deret Taylor mendapat nama dari matematikawan Inggris Brook Taylor. Bila deret tersebut terpusat di titik nol, deret tersebut dinamakan sebagai deret Maclaurin, dari nama matematikawan Skotlandia Colin Maclaurin.

Definisi Deret Taylor

Deret Taylor dari sebuah fungsi riil atau fungsi kompleks f(x) yang terdiferensialkan takhingga dalam sebuah pemetaan sebuah bilangan riil atau kompleks a adalah deret pangkat

f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f^{(3)}(a)}{3!}}(x-a)^{3}+\cdots

yang dalam bentuk lebih ringkas dapat dituliskan sebagai

\sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}\,(x-a)^{n}

dengan n! melambangkan faktorial n dan f⁽ⁿ⁾(a) melambangkan nilai dari turunan ke-n dari f pada titik a. Turunan kenol dari f didefinisikan sebagai fitu sendiri, dan (x − a)⁰ dan 0! didefinisikan sebagai 1.

Dalam kasus khusus di mana a = 0, deret ini disebut juga sebagai Deret Maclaurin.

Contoh Deret Taylor

Deret Maclaurin untuk setiap polinomial adalah polinomial itu sendiri.

Deret Maclaurin untuk (1 − x)⁻¹ merupakan deret geometri

1+x+x^{2}+x^{3}+\cdots \!

maka deret Taylor untuk x⁻¹ pada a = 1 adalah

1-(x-1)+(x-1)^{2}-(x-1)^{3}+\cdots .\!

Dengan melakukan integrasi deret Maclaurin di atas, dapat dihitung deret Maclaurin untuk log(1 − x), di mana log melambangkan logaritma natural:

-x-{\frac {1}{2}}x^{2}-{\frac {1}{3}}x^{3}-{\frac {1}{4}}x^{4}-\cdots \!

dan deret Taylor yang bersangkutan untuk log(x) pada a = 1 adalah

(x-1)-{\frac {1}{2}}(x-1)^{2}+{\frac {1}{3}}(x-1)^{3}-{\frac {1}{4}}(x-1)^{4}+\cdots ,\!

dan lebih umum, deret Taylor yang bersangkutan untuk log(x) pada suatu a = x₀ adalah:

\log(x_{0})+{\frac {1}{x_{0}}}(x-x_{0})-{\frac {1}{x_{0}^{2}}}{\frac {(x-x_{0})^{2}}{2}}+\cdots .

Deret Taylor untuk fungsi eksponensial e^x pada a = 0 adalah

1+{\frac {x^{1}}{1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {x^{5}}{5!}}+\cdots =1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+{\frac {x^{5}}{120}}+\cdots \!=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}.

Ekspansi di atas berlaku karena derivatif e^x terhadap x juga adalah e^x dan e⁰ sama dengan 1. Ini menyisakan elemen (x − 0)ⁿ pada numerator dan n! pada denominator untuk setiap elemen dalam jumlah tak terhingga.

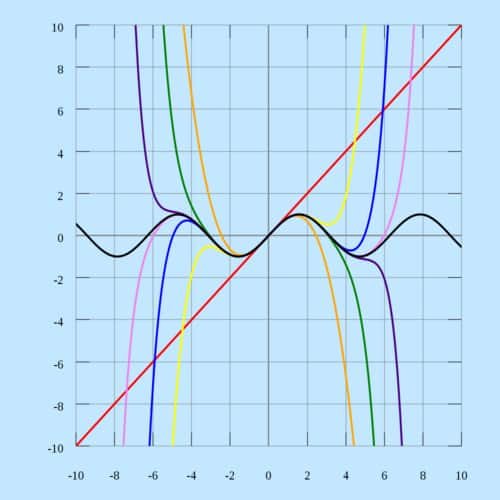
Deret Taylor matematika kalkulus — Deret Taylor. Seiring dengan meningkatya orde, polinomial Taylor mendekati fungsi yang dihampirinya. Gambar ini menunjukkan x (warna hitam) and hampiran Taylor, polinomial orde 1, 3, 5(lima), 7, 9, 11 and 13.

Teorema Taylor

Dalam kalkulus, teorema Taylor memberikan barisan pendekatan sebuah fungsi yang diferensiabel pada sebuah titik menggunakan suku banyak (polinomial). Koefisien polinomial tersebut hanya tergantung pada turunan fungsi pada titik yang bersangkutan. Teorema ini juga memberikan estimasi besarnya galat dari pendekatan itu. Teorema ini mendapat nama dari matematikawan Brook Taylor, yang menyatakannya pada tahun 1712, meskipun hasilnya sudah ditemukan pertama kali tahun 1671 oleh James Gregory

Teorema Taylor dalam satu variabel

Teorema Taylor menyatakan sembarang fungsi mulus dapat dihampiri dengan polinomial. Contoh sederhana penerapan teorema Taylor adalah hampiran fungsi eksponensial e^x di dekat x = 0:

{\textrm {e}}^{x}\approx 1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{n}}{n!}}.

Hampiran ini dinamakan hampiran Taylor orde ke-n’ terhadap e^x karena menghampiri nilai fungsi eksponensial menggunakan polinomial derajat n. Hampiran ini hanya berlaku untuk x mendekati nol, dan bila x bergerak menjauhi nol, hampiran ini menjadi semakin buruk. Kualitas hampiran dinyatakan oleh suku sisa:

$R_{n}(x)={\textrm {e}}^{x}-\left(1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots +{\frac {x^{n}}{n!}}\right).$

Lebih umum lagi, teorema Taylor berlaku untuk setiap fungsi yang dapat diturunkan ƒ, dengan hampiran untuk x di dekat titik a, dalam bentuk:

f(x)\approx f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dots {\frac {f^{(n)}(a)}{n!}}(x-a)^{n}.

Suku sisa adalah perbedaan antara fungsi dan polinomial hampirannya:

R_{n}(x)=f(x)-\left(f(a)+f'(a)(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+\dots {\frac {f^{(n)}(a)}{n!}}(x-a)^{n}\right).

Meskipun rumus eksplisit untuk suku sisa ini jarang digunakan, teorema Taylor juga memberikan estimasi nilai sisanya. Dengan kata lain, untuk x cukup dekat terhadap a, suku sisa haruslah cukup kecil. Teorema Taylor memberikan informasi persis seberapa kecil suku sisa tersebut.

Pernyataan Teorema Taylor

Pernyataan cermat teorema ini adalah sebagai berikut: bila n ≥ 0 adalah bilangan bulat dan f adalah fungsi yang terturunkan kontinu pada selang tertutup [a, x] dan terturunkan n + 1 kali pada selang terbuka (a, x), maka

f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f^{(2)}(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}+R_{n}(x).

Di sini n! melambangkan n faktorial dan R_n(x) adalah suku sisa, melambangkan beda antara polinomial Taylor derajat-n terhadap fungsi asli. Suku sisa R_n(x) tergantung pada x, dan kecil bila x cukup dekat terhadap a. Ada beberapa pernyataan untuk suku sisa ini.

Bentuk Lagrange dari suku sisa menyatakan bahwa terdapat bilangan ξ antara a dan x sedemikian sehingga

R_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}(x-a)^{n+1}.

Ini mengungkapkan teorema Taylor sebagai perampatan teorema nilai rata-rata. Sebenarnya, teorema nilai rata-rata digunakan untuk membuktikan teorema Taylor dengan suku sisa bentuk Lagrange.

Bentuk Cauchy suku sisa menyatakan bahwa terdapat bilangan ξ antara a dan x sehingga

R_{n}(x)={\frac {f^{(n+1)}(\xi )}{n!}}(x-\xi )^{n}(x-a).

Secara umum, bila G(t) adalah fungsi kontinu pada selang tertutup [a,x], yang terturunkan dengan turunan tidak nol pada (a,x), maka ada suatu bilangan ξ antara a dan x sehingga

R_{n}(x)={\frac {f^{(n+1)}(\xi )}{n!}}(x-\xi )^{n}\cdot {\frac {G(x)-G(a)}{G'(\xi )}}.

Ini mengungkapkan teorema Taylor sebagai generalisasi teorema nilai rata-rata Cauchy.

Bentuk di atas terbatas pada fungsi riil. Namun bentuk integral dari suku sisa juga berlaku untuk fungsi kompleks, yaitu:

R_{n}(x)=\int _{a}^{x}{\frac {f^{(n+1)}(t)}{n!}}(x-t)^{n}\,dt,

dengan syarat, seperti yang biasa ditemui, f_n kontinu mutlak dalam [a, x]. Ini menunjukkan teorema ini sebagai perampatan teorema dasar kalkulus.

Secara umum, suatu fungsi tidak perlu sama dengan deret Taylor-nya, karena mungkin saja deret Taylor tersebut tidak konvergen, atau konvergen menuju fungsi yang berbeda. Namun, untuk banyak fungsi f(x), kita dapat menunjukkan bahwa suku sisa R_n mendekati nol saat n mendekati ∞. Fungsi-fungsi tersebut dapat dinyatakan sebagai deret Taylor pada persekitaran titik a, dan disebut sebagai fungsi analitik.

Estimasi suku sisa

Versi umum teorema Taylor lainnya berlaku pada selang (a − r, a + r) tempat variabel x mengambil nilainya. Perumusan teorema ini memiliki keuntungan bahwa mungkin mengendalikan ukuran suku-suku sisa, dan dengan demikian kita dapat menghitung hampiran fungsi yang sahih pada seluruh selang, dengan batas yang cermat untuk mutu hampirannya.

Versi yang cermat untuk teorema Taylor dalam bentuk ini adalah sebagai berikut. Misalkan ƒ adalah fungsi yang terturunkan kontinu n kali pada selang tertutup [a – r, a + r] dan terturunkan n+ 1 kali pada selang terbuka (a − r, a + r). Bila ada konstanta positif riil M_n sedemikian sehingga |ƒ⁽ⁿ⁺¹⁾(x)| ≤ M_n untuk semua x ∈ (a − r, a + r), maka

f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f^{(2)}(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}+R_{n}(x),

di mana fungsi sisa R_n memenuhi ketidaksamaan (dikenal sebagai estimasi Cauchy)

|R_{n}(x)|\leq M_{n}{\frac {r^{n+1}}{(n+1)!}}

untuk semua x ∈ (a − r, a + r). Ini disebut sebagai estimasi seragam galat pada polinomial Taylor yang terpusat pada a, karena ini berlaku seragam untuk setiap x dalam selang.

Bila ƒ adalah fungsi mulus pada [a − r, a + r], maka konstanta positif M_n ada untuk tiapn = 1, 2, 3, … sedemikian sehingga | ƒ⁽ⁿ⁺¹⁾(x)| ≤ M_n untuk semua x ∈ (a − r, a + r). Tambahan lagi, jika mungkin memilih konstanta ini, sehingga

M_{n}{\frac {r^{n+1}}{(n+1)!}}\rightarrow 0

sebagai

n\rightarrow \infty ,\!

maka ƒ adalah fungsi analitik pada (a − r, a + r). Secara khusus, suku sisa pada hampiran Taylor, R_n(x) cenderung menuju nol secara seragam saat n→∞. Dengan kata lain, fungsi analitik adalah limit seragam dari polinomial Taylornya pada sebuah selang.

Pembuktian: satu variabel

Berikut adalah bukti teorema Taylor dengan suku sisa integral

Teorema dasar kalkulus menyatakan bahwa

\int _{a}^{x}\,f'(t)\,dt=f(x)-f(a),

yang dapat disusun ulang menjadi:

f(x)=f(a)+\int _{a}^{x}\,f'(t)\,dt.

Sekarang kita dapat melihat bahwa penerapan integrasi parsial ( kaidah yang mengubah integral perkalian fungsi menjadi bentuk lain, yang diharapkan lebih sederhana) menghasilkan:

{\begin{aligned}f(x)&=f(a)+xf'(x)-af'(a)-\int _{a}^{x}\,tf''(t)\,dt\\&=f(a)+\int _{a}^{x}\,xf''(t)\,dt+xf'(a)-af'(a)-\int _{a}^{x}\,tf''(t)\,dt\\&=f(a)+(x-a)f'(a)+\int _{a}^{x}\,(x-t)f''(t)\,dt.\end{aligned}}

Persamaan pertama diperoleh dengan memisalkan $u=f'(t)\,$ dandv = dt; persamaan kedua didapatkan dengan mencatat bahwa $\int _{a}^{x}\,xf''(t)\,dt=xf'(x)-xf'(a)$ ; yang ketiga didapatkan dengan mengeluarkan faktor yang sama.

Bila integrasi parsial ini diteruskan didapatkan:

f(x)=f(a)+(x-a)f'(a)+{\frac {1}{2}}(x-a)^{2}f''(a)+{\frac {1}{2}}\int _{a}^{x}\,(x-t)^{2}f'''(t)\,dt.

Dengan mengulangi proses ini, kita dapat menurunkan teorema Taylor untuk nilai n yang lebih tinggi.

Proses ini dapat diformalkan dengan menerapkan teknik induksi matematika. Jadi misalkan teorema Taylor berlaku unutk n tertentu, yaitu, misalkan

f(x)=f(a)+{\frac {f'(a)}{1!}}(x-a)+\cdots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}+\int _{a}^{x}{\frac {f^{(n+1)}(t)}{n!}}(x-t)^{n}\,dt.\qquad (*)

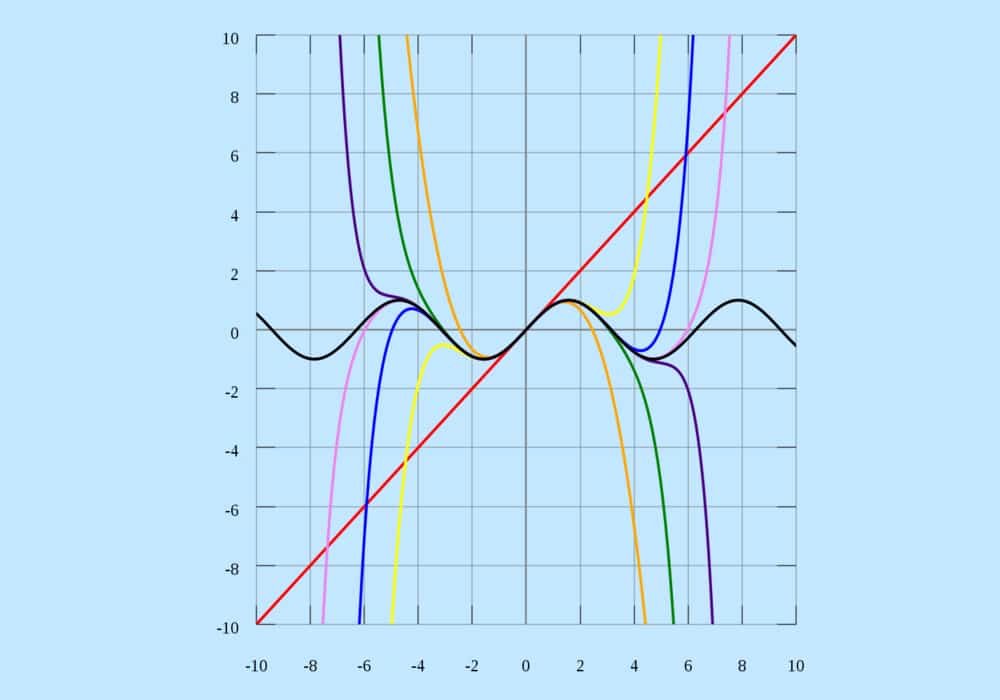
Kita dapat menulis ulang integral dengan integrasi parsial. Sebuah antiturunan (x − t)ⁿ sebagai fungsi dari t diberikan sebagai −(x−t)ⁿ⁺¹ / (n + 1), sehingga