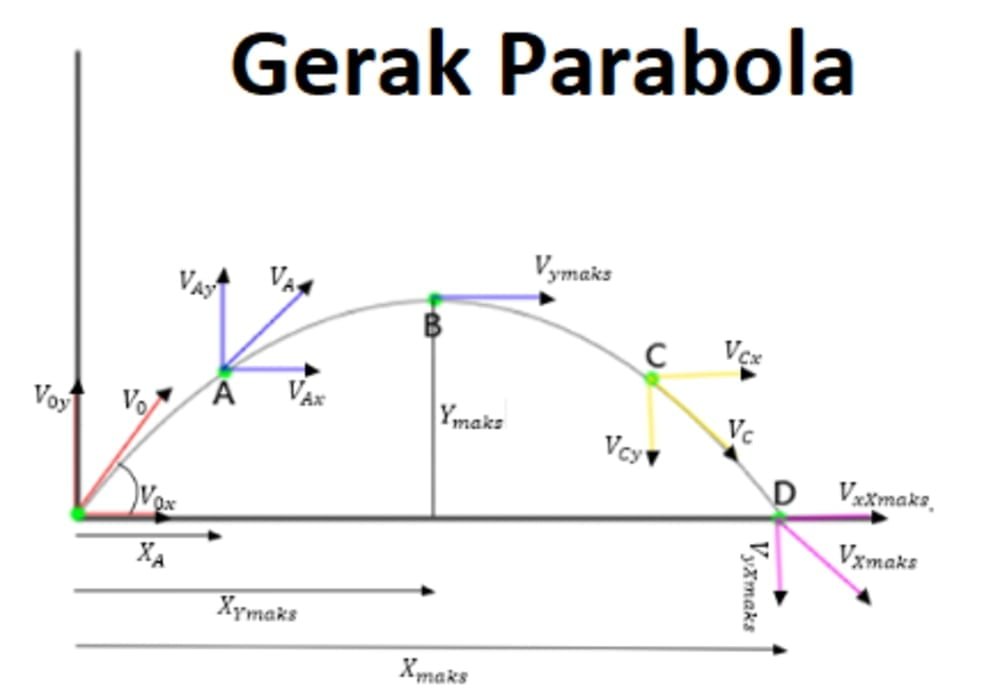
Penjelasan Gerak Parabola

Pengertian dari gerak parabola adalah merupakan sebuah gabungan dari gerak lurus beraturan (GLB) pada sumbu x (horizontal) dan gerak lurus berubah beraturan (GLBB) yaitu pada sumbu y (vertikal).

Gerak parabola disebut gerak peluru karena gerak ini mirip dengan peluru yang ditembakkan. Pada gerak parabola, penyebab gerakan benda dan gesekan udara dapat diabaikan. Kita hanya akan terfokus pada gerakan benda setelah diberi kecepatan awal dan bergerak dalam lintasan melengkung daerah gaya gravitasi bekerja.

Rumus Gerak Parabola

Pada sumbu x untuk gerak parabola telah di tetapkan untuk beberapa rumus di bawah ini yaitu:

Vx = Vοx = Vο cos θ

X = Vοx t = Vο cos θ  x t

Namun pada sumbu y untuk gerak parabola berlaku persamaan GLBB yaitu:

Vοy = Vο sin θ

Dan gerak vertikal ke atas menggunakan rumus gerak parabola sebagai berikut yakni:

Vy = Vοy – gt = Vο sin θ – gt

Y = Vοy t – ½ gt²

Setelah di dapat kecepatan dari sumbu x nya yaitu ( Vx ) dan kecepatan dari sumbu y nya yaitu ( Vy ), kita bisa mencari sebuah nilai kecepatan total nya yaitu ( Vg ), dengan menggunakan rumus resultan kecepatan yaitu seperti pada rumus di bawah ini:

Rumus resultan kecepatan:

Vr­ = √ Vx ² + Vy ² maka, tan θ = Vy / Vx

Keterangan :

• Vox = kecepatan awal sumbu x ( m/s )
• Voy = kecepatan awal sumbu y ( m/s ) vx = kecepatan setelah waktu ( t ) tertentu pada sumbu ( m/s )
• Vy = kecepatan setelah waktu nya ( t ) tertentu pada sumbu y ( m/s )
• Vr = kecepatan total ( m/s )
• x = kedudukan benda pada sumbu x nya ( horizontal ) ( m )
• y = kedudukan benda nya pada sumbu y ( vertikal ) ( m )
• t = waktu ( s )
• g = percepatan gravitasi ( m/s )
• θ = sudut elevasi ( º )

Pada Titik A

Seperti yang sudah dikemukakan di atas, gerak pada sumbu x kita analisis dengan Gerak Lurus Beraturan (GLB). Maka untuk kecepatan V_x sama dengan kecepatan V_0x, sedangkan untuk V_ytergoda oleh gravitasi yang menarik dan unik benda ke bawah(GLBB), sehingga kecepatan berkurang.

Untuk jarak horizontal digunaka rumus jarak Gerak Lurus Beraturan, sedangkan untuk jarak vertikal atau tinggi dicari menggunkan rumus jarak Gerak Lurus Berubah Beraturan.

melalui atau bersama ini demikian kita sanggup merumuskan beberapa persamaan, yaitu :

Rumus Gerak Parabola Pada Titik B  y_maks atau h

Berikut ini beberapa persamaan yang sanggup kita rumuskan ketika melalui titik B (titik maksimum) :

Titik B ini yaitu titik tertinggi dimana kita simbolkan sebagai y_maks atau h. Agar sebuah benda sanggup mencapai ketinggian maksimum maka syaratnya yaitu V_y = 0, maka kecepatan pada titik tertinggi yaitu kecepatan pada sumbu x (V_x ).

Pada Titik C

Untuk gerak parabola pada titik C sama menyerupai gerak parabola pada titik A. Perbedaanya yaitu gerak gravitasi yang bernilai faktual alasannya yaitu menuju ke bawah.

Karena dikatakan sama menyerupai melalui titik A, maka gerak pada sumbu x tetap memakai GLB dan untuk y memakai GLBB (namun gravitasinya bernilai positif).

Bersama ini demikian kita dapat merumuskan beberapa persamaan, yaitu :

Pada Titik D Terjauh atau X_maks

Berikut ini beberapa persamaan gerak parabola pada titik D:

A. Kecepatan pada sumbu x
V_x = V_0x = V₀ . cos θB. Kecepatan pada sumbu y
V_y = V₀ sin θ + gt

C. Waktu yang dibutuhkan hingga ke tanah (titik D)
t = 2.

t =

D. Jarak maksimum (Jarak dari awal bola bergerak hingga titik D)
X_maks =

Keterangan

• V₀ ialah kecepatan awal
• V_0x ialah kecepatan awal pada sumbu x
• V_x ialah kecepatan pada sumbu x
• V_0y ialah kecepatan awal pada sumbu y
• V_y ialah kecepatan pada sumbu y
• g ialah gravitasi
• t ialah waktu tempuh
• X ialah jarak terhadap sumbu x
• X_maks ialah jarak maksimum

Titik D ini yaitu jarak terjauh yang dilalui oleh sebuah benda yang melaksanakan gerak parabola. Pada gambar kita simbolkan jarah terjauh ini dengan simbol X_maks. Jarak maksimum ini sanggup juga dikatakan jarah sebuah objek kembali ke tanah sehabis objek tersebut melaksanakan gerak parabola.

Waktu yang dibutuhkan sebuah benda untuk hingga ke tanah yaitu 2 kali waktu benda tersebut untuk mencapai jarak ketika berada di titik tertinggi.

Koordinat Tempat Kedudukan Setiap Saat (TK)

Tempat kedudukan benda setiap saat dinyatakan dengan koordinat TK = (X_t, Y_t)

Menentukan Waktu Pada Titik Puncak Atau (Ketinggian Maksimum) dan Waktu Pada Ketinggian Semula – Gerak Parabola

Ketinggian maksimum di capai pada saat sebuah benda mencapai titik tertinggi pada sumbu y. Pada ketinggian maksimum, kecepatan benda di titik tersebut iyalah 0 ( Vy = 0 ).

Dan secara matematis, rumus untuk menentukan waktu ketinggian maksimum di tuliskan seperti di bawah ini:

Tp = ( Vo sin θ ) : g

Dan untuk kembali ke posisi semula ( mencapai jarak maksimum ) dari keadaan awal, rumus yang di gunakan harus di kali angka 2 dari waktu untuk mencapai ketinggian maksimum.

Dan secara matematis, rumus untuk menentukan waktu kembali ke posisi semula di tuliskan seperti di bawah ini:

tt­ = 2 x tp = 2 x ( Vo sin θ ) / g

Rumus Menentukan Ketinggian Maksimum (hmax)

Untuk menentukan ketinggian maksimum, rumus yang di gunakan iyalah sebagai berikut :

h_max = ( Vo² sin² θ ) / 2g

Rumus Menentukan Jangkauan Maksimum (x_max)

Selain ketinggian maksimum, kita juga bisa menghitung jangkauan maksimum. Pengertian dari jangkauan maksimum sendiri merupakan jarak maksimum yang di jangkau pada sumbu horizontal ( sumbu x ). Dan jangkauan maksimum di rumuskan sebagai berikut :

X_max =  ( 2Vo² sin θ cos θ ) / g

Keterangan :

• g = percepatan gravitasi ( m/s² )
• θ = sudut elevasi ( º )
• Vº = kecepatan awal ( m/s )
• X_max = jangkauan maksimum ( m )
• h_max = ketinggian maksimum ( m )
• tp = waktu mencapai titik puncak nya ( s )
• tt = waktu mencapai jarak maksimum nya ( s )

Contoh Soal dan Jawaban Gerak Parabola

1. Sebuah peluru ditembakkan secara mendatar dengan kelajuan 50 m/s dari sebuah meriam dari atas sebuah gunung, Jika percepatan gravitasi bumi yakni 10 m/s², dan ketinggian bukit 100 m. Berapa Waktu yang diperlukan peluru untuk menyentuh tanah dan berapa jarak mendatar yang dicapai peluru tersebut ?

Penyelesaian :

Diketahui :

• Percepatan gravitasi bumi = 10 m/s2
• Ketinggian bukit = 100 m

Ditanya :

• Waktu yang diperlukan peluru untuk mencapai tanah
• Jarak mendatar yang dicapai peluru (s)

Pembahasan :

a) Waktu yang diperlukan peluru untuk mencapai tanah

Y = ½ gt²
Y = ½ g t2
100 = (½)(10) t2
t = √20 = 2√5 sekon

Jadi, waktu yang diperlukan peluru mencapai tanah adalah 2√5 sekon

b) Jarak mendatar yang dicapai peluru (S)

S = V t
S = (50)( 2 √5) = 100 √5 meter

Jadi, Jarak mendatar yang dicapai oleh peluru tersebut adalah 100 √5 meter.

2. Sebutkan beberapa faktor yang mempengaruhi gerak parabola!

Gerak pearabola dipengaruhi oleh beberapa faktor yaitu:

• Benda tersebut bergerak karena ada gaya yang diberikan. Gaya Pada kesempatan ini, belum menjelaskan bagaimana proses benda-benda tersebut dilemparkan, ditendang dan diberi gaya pada umumnya. Kita hanya memandang gerakan benda tersebut setelah dilemparkan dan bergerak bebas di udara hanya dengan pengaruh daripadah gravitasi.
• Seperti pada Gerak Jatuh Bebas, benda-benda yang melakukan gerak parabola dipengaruhi oleh gravitasi, yang berarah ke bawah menuju pusat bumi dengan besar g = 9,8 m/s2.
• Hambatan atau gesekan udara. Setelah benda tersebut benda tersebut diberikan kecepatan awal hingga bergerak, maka selanjutnya gerakannya bergantung kepada gravitasi atau gesekan pada hambatan udara. Karena kita menggunakan model ideal, maka dalam menganalisis gerak parabola selalu berpengaruh terhdap gravitasi.

3. Sebuah peluru ditembakkan dari moncong sebuah meriam dengan kelajuan 50 m/s arah mendatar dari atas sebuah bukit, dengan ilustrasi seperti berikut:

•  percepatan gravitasi bumi = 10 m/s2

• ketinggian bukit = 100 m

Tentukan :
a. Waktu yang diperlukan peluru untuk mencapai tanah
b. Jarak mendatar yang dicapai peluru (S)

Pembahasan

a) Waktu yang diperlukan peluru untuk mencapai tanah

Pada saat meninjau pada sumbu Y, yakni merupakan suatu gerak bebas. Sehingga Voy = O dan ketinggian bukit namakan Y (di soal dinamakan h)

• Y = 1/2 g t2
• 100 = (1/2)(10) t2
• t = √20 = 2√5 sekon

Jadi, waktu yang diperlukan peluru mencapai tanah yaitu 2√5 sekon

b) Jarak mendatar yang dicapai peluru (S)

Yakni berupa dengan GLB oleh sebab pada sudutnya nol terhadap horizontal dan rumusnya:

• S=Vt
• S=(50)(2√5)=100√5meter

Maka,  Pada jarak datar yang dicapai peluru (S) ialah 100 √5 meter.

4. Budi menembakkan peluru dengan kecepatan awal 120 m/s membentuk sudut elevasi 30° terhadap permukaan tanah. Jika g = 10 m/s2, peluru mencapai titik tertinggi setelah…

a. 4 s
b. 5 s
c. 6 s
e. 7 s
d. 8 s

Jawaban : C

Pembahasan :
Vo = 120 m/s
θ = 30°
Waktu untuk mencapai titik tertinggi = tp

Jadi waktu yang diperlukan untuk mencapai puncak atau titik tertinggi adalah 6 sekon.

5. Sebuah benda dijatuhkan dari pesawat terbang yang melaju horisontal dengan kelajuan 360 km/jam pada ketinggian 4500 m. Benda akan jatuh pada jarak horisontal sejauh (g = 10 m/s²)…

a. 1.000 m
b. 2.000 m
c. 2.400 m
d. 3.000 m
e.  4.000 m

Jawaban : D

Pembahasan :
Vo = 360 km/jam = 100 m/s
h = 4500 m
X = …………….?

“INGAT : Gerak setengah parabola, Gerak vertikal ke bawah = Gerak jatuh bebas dan Gerak horizontal = Geral Lurus Beraturan”.

Jadi benda tersebut atuh pada jarak 3000 m dari jarak horizontal pesawat.

6. Seorang pemain sepakbola menendang bola dengan sudut elevasi 60°. Jika bola bergerak dengan kecepatan awal 30 m/s, maka jarak pemain yang menerima umpan kiper tersebut mendekati…

a. 60 m
b. 65 m
c. 70 m
d. 75 m
e. 78 m

Jawaban : E
Pembahasan :
Vo = 30 m/s
θ = 60°

Arak horizontal maksimum = X_max

Jadi jarak pemain yang menerima umpan kiper adalah 78 m.

7. Apabila besar sudut antara arah horizontal dan arah tembak suatu peluru adalah 53°, perbandingan antara jarak tembak dalam arah mendatar dengan tinggi maksimum peluru adalah…. (sin 53° = 4/5 )

a. 2 : 3
b. 3 : 2
c. 3 : 1
d. 1 : 3
e. 2 : 1

Jawaban : C
Pembahasan :

Jadi perbandingan jangkauan maksimum dan ketinggian maksimum adalah 3 : 1

8. Seorang pengemudi mobil offroad hendak melewati sebuah rintangan berupa parit sepanjang 7,5 m dengan perbedaan ketinggian sebesar 1,8 m. Maka kecepatan mobil minimum agar mobil tidak masuk ke dalam parit adalah…

a. 7,5 m/s
b. 10 m/s
c. 12,5 m/s
d. 15 m/s
e. 20 m/s

Jawaban : C
Pembahasan

Jadi kecepatan minimum mobil agar tidak masuk ke dalam parit adalah 12,5 m/s

9. Jika sebuah selang air menyemprotkan air ke atas dengan kecepatan 10 m/s pada sudut 37^o berapakah jarak tempuh maksimum air tersebut.

a) 9,3
b) 7,8
c) 8,6
d) 9,6
e) 5,7

Pembahasan:

Dik : vo = 10 m/s; θ =  37^o.
xmax = (vo² sin 2θ)/g
⇒ xmax = (100 . 2 sin 37^o cos 37^o )/10
⇒ xmax = 20 (3/5) (4/5)
⇒ xmax = 9,6 m.
Jadi, air tersebut akan menyentuh tanah pada jarak 9,6 m dari selang.

10. Peluru A dan B ditembakkan dari senapan yang sama dengan sudut elevasi berbeda. Peluru A dengan sudut 30^o dan peluru B dengan sudut 60^o. Tentukanlah perbandingan tinggi maksimum yang dicapai peluru A dan peluru B.

a)¼
b)1/3
c)1/6
d)1/5
e)1/2

Pembahasan:
Dik : θA = 30^o ; θB = 60^o .
hmax = (vo² sin² θ)/ 2g
⇒ hmaxA = (vo² sin² θA)/ 2g dan hmaxB = (vo² sin² θB)/ 2g.
Dari rumus di atas jelas terlihat bahwa ketinggian maksimum berbanding terbalik dengan gravitasi dan berbanding lurus dengan kuadrat kecepatan awal dan sudut elevasi. Karena kecepatan awal peluru dan gravitasi sama, maka perbandingan antara ketinggian maksimum A dan B hanya bergantung pada besar sudut elevasi masing-masing peluru.
hmaxA / hmaxB = sin² θA/ sin² θB
⇒ hmaxA / hmaxB = sin² 30^o/ sin² 60^o
⇒ hmaxA / hmaxB = (½)² / (½√3)²
⇒ hmaxA / hmaxB = (1/4) / (3/4)
⇒ hmaxA / hmaxB = 1/3

11. Sebuah meriam menembakkan peluru dengan kecepatan 78,4 m/s. Jika sudut elevasi tembakan 30°, hitung waktu peluru untuk mencapai titik tertinggi! (g = 9,8 m/s²)

a. 5s
b. 3s
c. 4s
d. 6s
e. 10s

Penyelesaian :

Diketahui:
V₀ = 78,4 m/s
α = 30°

Ditanyakan:
t_H =…?

Jawab :

Peluru mencapai titik terang tertinggi setelah menempuh gerak selama 4 sekon.

12. Michael menendang bola dengan kecepatan awal pada arah vertikal 9 m/s dan kecepatan awal pada arah mendatar 12 m/s. Tentukanlah besar kecepatan awal bola tersebut yang Michael tendang.

a)15 m/s
b)14 m/s
c)17 m/s
d)23 m/s
e)16 m/s

Pembahasan
Dik : vox = 12 m/s ; voy = 9 m/s.
vo = √(vox² + voy²)
⇒ vo = √(12² + 9²)
⇒ vo = √(144 + 81)
⇒ vo = √224
⇒ vo =15 m/s.
Jadi, kecepatan awal bola tersebut adalah 15 m/s.

13. Sebuah bola ditendang dengan sudut elevasi 53^o dan kecepatan awal 5 m/s. Tentukanlah jarak tempuh maksimum yang akan dicapai bola tersebut.

a)2,8 M
b)2,4 M
c)2,5 M
d)2,7 M
e)2,3 M

Pembahasan:
Dik : vo = 5 m/s; θ = 53^o
xmax = (vo² sin 2θ)/g
⇒ xmax = (25 . 2 sin 53^o cos 53^o )/10
⇒ xmax = 5 (4/5) (3/5)
⇒ xmax = 2,4 m.
Jadi, jarak maksimum bola hanya 2,4 meter.

14. Jika sebuah peluru ditembakkan dengan sudut elevasi 37^odan kecepatan awal 10 m/s, maka tentukanlah kecepatan peluru setelah 0,4 detik.

a) 1√17 m/s.
b) 2,5√17 m/s.
c) 2,4√17 m/s.
d) 2√17 m/s.
e) 2

Pembahasan:
Dik : vo = 10 m/s; t = 0,4 s; θ = 37^o
Untuk mengetahui kecepatan peluru setelah 3 detik maka kita harus menentukan terlebih dahulu vx dan vy setelah 3 detik sebagai berikut :
vx = vox (Ingat bahwa GLB kecepatannya tetap)
⇒ vx = vo cos θ
⇒ vx = 10 cos 37^o
⇒ vx = 10 (4/5)
⇒ vx = 8 m/s
vy = voy – g.t (dalam arah vertikal berlaku GLBB)
⇒ vy = vo sin θ – g.t
⇒ vy = 10 sin 37^o – 10.(0,4)
⇒ vy = 10 (3/5) – 4
⇒ vy = 6 – 4
⇒ vy = 2 m/s
vt = √(vx² + vy²)
⇒ vt = √(8² + 2²)
⇒ vt = √68
⇒ vt = 2√17 m/s.

15. Tentukan ketinggian maksimum yang dicapai oleh sebuah bola yang ditendang dengan kecepatan awal 5 m/s pada sudut elevasi 37^o.

a) 0,36
b) 0,45
c) 0,67
d) 0,23
e) 0,47

Pembahasan:
Dik : vo = 5 m/s;  θ = 37^o
hmax = (vo² sin² θ)/ 2g
⇒ hmax = (5² sin² 37^o)/ 2(10)
⇒ hmax = {25 (9/25)}/ 20
⇒ hmax = 9/20
⇒ hmax = 0,45 m
Jadi, ketinggian maksimum yang dicapai bola adalah 0,45 meter. [b]

16. Sebuah peluru meriam ditembakkan dengan kecepatan awal 60 m/s dan sudut elevasi 53°. Bilag =   10 m/s² maka posisi peluru pada detik ke-1 adalah…

A. x = 36 m, y = 64 m
B.   x = 64 m, y = 43 m
C.   x = 36 m, y = 43 m
D.   x = 32 m, y = 32 m
E.   x = 43 m, y = 36 m

Pembahasan:

Gunakan rumus gerak parabola!

Data-data yang diketahui pada soal:

v_o = 60 m/s
g  = 10 m/s²
t   = 1 s
α  = 53°

Sudut α = 53° merupakan sudut segitiga siku-siku yang bisa digambarkan sebagai berikut:

Sin 53 =4/5

Cos 53=3/5

Tan 53=4/3

Gerak horizontal pada gerak parabola merupakan gerak lurus beraturan (GLB), sehingga:

x = v_o cos α . t
= 60 . cos 53° . 1
= 60 . 3/5 . 1
= 36

Sedangkan gerak vertikal pada gerak parabola merupakan gerak lurus berubah beraturan (GLBB), sehingga:

y = v_o sin α − ½gt²
= 60 . sin 53° − ½ . 10 . 1²
= 60 . 4/5 − 5
= 48 − 5
= 43

Jadi, posisi peluru pada detik ke-1 adalah x = 36 m, y = 43 m (C).

17. Tentukanlah waktu yang dibutuhkan untuk mencapai ketinggian maksimum jika sebuah batu dilempar dengan sudut elevasi 30^o dan kecepatan awal 6 m/s.

a) 0,5
b) 0,6
c) 0,3
d) 0,2
e) 0,9

Pembahasan:

Gunakan rumus gerak parabola!
Dik : vo = 6 m/s;  θ = 30^o
tp = (vo sin θ)/g
⇒ tp = (6 sin 30^o)/10
⇒ tp = 0,6 (½)
⇒ tp = 0,3 detik.
Jadi waktu yang dibutuhkan adalah 0,3 detik.

18. Peluru yang ditembakkan oleh seorang Bapak Polisi, ditembakkan dengan kecepatan 60 m/s dan sudut elevasi θ = 30^o. Jika g = 10 m/s², kecepatan peluru setelah bergerak 2 sekon adalah…

a) vx = 10 m/s dan vy = 20 m/s
b) vx = 20 m/s dan vy = 30√3 m/s
c) vx = 30√3 m/s dan vy = 10 m/s
d) vx = 30√3 m dan vy = 30 √3 m/s

Pembahasan:

Kecepatan peluru untuk sumbu x:
vx = v₀ cos θ = 60 m/s . 1/2√3 = 30√3 m/s

Kecepatan peluru untuk sumbu y:
vy = v₀ sin θ – g . t = 60 m/s . 1/2 – (10 m/s2 . 2s) = 30 m/s – 20 m/s = 10 m/s

Jawaban: C

19. Sebuah peluru dengan massa 20 gram ditembakkan pada sudut elevasi 60° dan kecepatan 40 m/s. Jika gesekan dengan udara diabaikan maka energi kinetik peluru pada titik tertinggi adalah…

A. 0 joule
B. 4 joule
C. 8√2 joule
D. 12 joule
E. 24 joule

Penyelesaian:

Data-data yang diketahui pada soal:

m = 20 gram = 0,02 kg
v_o = 40 m/s

α  = 60°
cos α  = ½

Di titik tertinggi, kecepatan gerak peluru ke arah vertikal sama dengan nol (v_y = 0) sehingga yang berperan hanya kecepatan ke arah horizontal (v_x).

v_x = v_o cos α
= 40 . cos 60° m/s
= 40 . ½ m/s
= 20 m/s

Energi kinetik di titik tertinggi adalah

E_k = ½mv_x²
= ½ . 0,02. 20²
= 4

Jadi, energi kinetik peluru di titik tertinggi adalah 4 joule (B)

20. Ketika benda bergerak menempuh lintasan gerak parabola, besaran manakah dari di bawah ini yang konstan (tetap)? ditanya:
– Kelajuan
– Percepatan
– Komponen horizontal kecepatan
– Komponen vertikal kecepatan

a) A dan B
b) B dan C
c) C dan D
d) D dan A

Jawab:

• Kelajuan, nilai v_xkonstan, namun nilai v_ydipengaruhi oleh waktu (t), sehingga kelajuan nilainya tidak konstan.

• Percepatan, a_y= -g nilai percepatan gravitasi Bumi adalah konstan. nilai percepatan gravitasi Bumi alah konstan, sehingga percepatan nilainya

• • Komponen horizontal kecepatan, v_x= v₀. cos α dimana nilaiv₀ dan α adalah konstan,sehingga komponen horizontal kecepatan adalah konstan.

• Komponen vertical kecepatan, v_y= v₀. sin α – g . t dimana nilainya dipengaruhi oleh waktu (t) dan tidak mungkin konstan.

Jadi jawaban yang benar adalah A dan B

21. Sebuah pesawat terbang bergerak mendatar dengan kecepatan 200 m/s melepaskan bom dari ketinggian 500 m. Jika bom jatuh di B dan g = 10 m/s², maka jarak AB adalah…

a) 400 m
b) 500 m
c) 600 m
d) 750 m
e) 1000 m

Jawaban: E

• Kecepatan pesawat dalam arah mendatar, v_x = 200 m/s
• Ketinggian pesawat terhadap tanah, h = 500 m
• Percepatan gravitasi, g = 10 m/s²

22. Sebuah benda dilempar miring ke atas sehingga lintasan gerak parabola, seperti pada gambar di samping. Pada saat jarak tempuh mendatarnya (x) = 20 m, maka ketinggiannya (y) adalah…

a) 5 m
b) 10 m
c) 15 m
d) 20 m
e) 25 m

Jawaban: C

Gerak parabola:

• Kecepatan awal benda, v₀ = 20 √2 m/s

• Percepatan gravitasi, g = 10 m/s²

• Sudut elevasi, θ₀ = 45^o

22. Posisi arah vertikal (ketinggian) benda saat jarak tempuh mendatarnya, x = 20 meter adalah:

a) 17
b) 21
c) 11
d) 15

Pembahasan :

y = (tan θ₀)x – g/2v₀² cos² θ₀ x²
= (tan 45^o) x 20m – 10m/s²/2x(20√2 m/s)² x (cos 45^o)² x (20m)²
= (1)(20m) – (4000 m³ / s²)/2(800m² / s²)(1/2)
= 15 m.

Jadi jawabannya adalah D.

23. Sebuah benda dijatuhkan dari pesawat terbang yang bergerak horizontal dengan kelajuan 360 km/jam pada ketinggian 500 m. Tentukan jarak horizontal jatuhnya benda tersebut!

a) 500 M
b) 800 M
c) 1000 M
d) 250 M

Penyelesaian:

Diketahui:

v₀ = 360 km/jam = 100 m/s
y = 500 m
α= 0^o (horizontal)

Ditanyakan:

R = … ?

Jawab:

y = v₀ . Sin α . t – 1/2 gt², karena α = 0^o maka:
y = – 1/2 gt²
-500 = – 1/2 .10 . t²
t² = 100
t = 10 sekon

Pada arah horizontal
R = v₀ . Cos α .t = 100 . cos 0^o . 10 = 1.000 m

Jadi jawabannya adalah 1000 m.

24. Seorang stuntman melaju mengendarai sepeda motor menuju ujung tebing setinggi 50 m. Berapa kecepatan yang harus dicapai motor tersebut saat melaju dari ujung tebing menuju landasan dibawahnya sejauh 90 m dari tebing? Abaikan gesekan udara.

a) 28.21 m/s
b) 30.11 ms
c) 28.45 m/s
d) 45.00 m/s

Pembahasan:
Gambarkan terlebih dahulu lintasan objek tersebut. Perhatikan gambar dibawah ini:

Kemudian kita identifikasi komponen-komponen yang diketahui,
m.
, jadi kita tahu bahwa
Dengan rumus untuk mencari jarak tempuh, kita bisa mendapatkan kecepatan motor:
Jadi, kecepatan yang harus dicapai harus sebesar 28,21 m/s atau sekitar 100 km/h (101,55 km/h). [A]

25. Sebuah peluru ditembakkan dengan kecepatan 60 m/s dan sudut elevasi 30°. Ketinggian maksimum yang dicapai adalah…

A. 30 m
B. 45 m
C. 50 m
D. 90 m
E. 100 m
Pembahasan
Data dari soal:
v_o = 60 m/s
α = 30°
Y_maks = ……

                v_o ² sin² α
Y_maks = ^{_______________________}
                         2g

                  (60) ² (sin 30° )²
Y_maks = ^{_______________________}
                        2(10)

                       (60) ² (1/2 )²
Y_maks = ^{_______________________} = 45 meter
                           20

26. Peluru ditembakkan condong ke atas dengan kecepatan awal v = 1,4 x 10³ m/s dan mengenai sasaran yang jarak mendatarnya sejauh 2 x 10⁵ m. Bila percepatan gravitasi 9,8 m/s², maka elevasinya adalah n derajad, dengan n sebesar…

A. 10
B. 30
C. 45
D. 60
E. 75
Pembahasan
Data dari soal:
v_o = 1,4 x 10³ m/s
Xmaks = 2 x 10⁵ m
α = …….

Dari rumus jarak mendatar maksimum:

                      v_o ² sin 2 α
X_maks = ^{_______________________}
g
                       (1,4 x 10³) ² sin 2 α
2 x 10⁵ = ^{______________________________}
                                  9,8

                                 2 x 10⁵ x 9,8
sin 2 α = ^{______________________________}
                           (1,4 x 10³) ²

sin 2 α = 1
sin 2α = sin 90°
α = 90°/₂ = 45 °

27. Bom dilepas dari pesawat tempur, karena kecepatan pesawat dalam arah vertikal nol (v_y = 0), maka bom dalam arah vertikal mengalami jatuh bebas, maka waktu yang diperlukan untuk sampai di sasaran (titik B) adalah:

a) 1000 m
b) 2000 m
c) 2500 m
d) 1500 m
e) 4000 m

t = √2h/g
= (2x500m/10m/s²)
= 10 s

Jarak mendatar (AB) adalah:

x = v_x t
= (200 m/s) (10 s)
= 2.000 m.

28. Sebuah bom dijatuhkan di kota Hirosima dari pesawat tempur tanpa kecepatan awal relatif terhadap pesawat. Jika ketinggian pesawat tempur 200 m dan jarak mendatar antara sasaran dengan pesawat tempur 600 m, maka kecepatan pesawat tempur relatif terhadap sasaran mendekati…

A. 745 km/jam
B. 420 km/jam
C. 360 km/jam
D. 340 km/jam
E. 200 km/jam

Pembahasan:
Waktu yang diperlukan bom sampai ditanah
h = 1/2 g t²
200 = 1/2 (10) t²
5 t² = 200
t = √40 = 6,2 s
Pada arah mendatar (sumbu x):
x = v . t
v = x / t = 600 m / 6,2 s = 96,8 m/s = 348 km/jam
Jawaban: D.

29. Jika sebuah diagram menunjukkan lintasan sebuah proyektil yang ditembakkan dengan kecepatan horizontal v dari atap gedung setinggi h. Harga-harga v dan h berikut akan menghasilkan θ terbesar adalah…

A. v = 10 m/s dan h = 30 m
B. v = 10 m/s dan h = 50 m
C. v = 30 m/s dan h = 30 m
D. v = 30 m/s dan h = 30 m
E. v = 50 m/s dan h = 10 m

Pembahasan:

Supaya θ sebesar-besarnya maka tan θ harus sebesar-besarnya. Karena tan θ = vy / vx maka vy harus yang terbesar dan vx = v harus yang terkecil.
Rumus vy = √2gh maka harga vy menjadi besar jika h besar
Jawaban: B.

30. Sebuah benda dtembakkan Vertikal  keatas dengan kecepatan awal 100 m/s. Percepatan grafitasi bumi 10 m/s² , secara berurut. Berapakah :  a).  waktu untuk mencapai tinggi maksimum ? b).  tinggi maksimum yang dicapai  oleh benda ?

a. (11, 1000)
b. (10, 500)
c. (5, 500)
d. (20, 100)

     Diketahui :     Vo = 100 m/s
g = 10 ms^-2

      Ditanya   :  a).  t  = ……?
b).  h _max

      Jawab  :   a).   t  = Vo sin α / g
=  (100 m/s). sin 90^o / 10 ms^-2
                                 =  10 s

                      b).  h max  =  (Vo sin α) ² / 2g
=  [(100 m/s). sin 90^o]² / 2. 10 ms^-2
                                         =  [(100 m/s). 1 ]² / 20. Ms^-2
                                         =  10.000 m².s^-2 /20. ms^-2
                                         =  500 m

Jawabannya : B

31. Sebuah  mobil Tank  alat  tempur menembakkan peluru dari moncong meriam dengan kecepatan awal 150 m/s  membentuk sudut elevasi 60^o (g = 10 ms^-2). Berapakah secara berurut:
1. Tinggi maksimum yang dapat dicapai oleh peluru
2. Waktu yang diperlukan oleh peluru untuk mencapai titik sasaran
3.  Jauh sasaran yang bisa dicapai oleh peluru

a) 785m ,28 s, 2000m
b) 843.75 m ,25,5 s, 1912,5 m
c) 678,75 m, 27 s, 1356 m
d) 834.22 m, 31 s ,567 m

Pembahasan :

Diketahui :    Vo = 150 m/s
g  = 10 ms-2
α  =  60⁰

 ditanya    :    a). h max   = …?
b).  t _tota   = …?
c).  S…?

Jawab :  a).  Waktu yang diperlukan untuk mencapai titik tertinggi :

                        t  = Vo sin α / g
= 150 ms^-1. Sin 60⁰ / 10 ms^-2
                                   = 15  s. ½ V3
= 12,75 s

                            h max  =  (Vo sin α) ² / 2g
=  (150 ms^-1. Sin 60⁰)² /2. 10 ms^-2
                                    =  ( 150 ms-¹. ½ V3)²/ 20 ms^-2
                                    =  (75 V3) m2 s^-2 / 20 ms^-2
                                        =  16875 m/20
=  843,75 m

                   b). t _total  = t _naik + t _turun
                          t _naik =  t _turun  = 12.75 s
maka   t _total  =  t _naik + t _turun
                                                    =  2t _naik = 2t _turun
                                                             =  2. 12,75 s
=  25,5 s

                   c).  S = Vo² . sin 2 α/g
=  (150 ms^-1)² sin 120⁰/10 ms^-1
                             =  22500 m² s^-2. ½ v3  /10 ms^-1
                             =  2250 . ½ v3  m
=  1912,5 m

Jadi jawabannya adalah  [B]

32. Sebuah benda di jatuhkan dari Puncak suatu menara tanpa kecepatan awal. Setelah 3 detik benda menyentu tanah  (g = 10 ms^-1) , berapakahtinggi menara itu dari permukaan tanah?

a) 56 M
b) 45M
c) 23M
d) 50M

Pembahasan :

Gunakan rumus gerak parabola!

      Diketahui :  t = 3 s
g = 10 m.s^-2
                       Vo = 0

       Ditanya :  h  =  …?

      Jawab :  Y_turun = h _turun = V_o t + ½ g t²
                                =  0. 3 s  + ½ .10 m.s^-2 (3 s)²
                                =  0  + 5.9 m
=  45 m.

33. Sebuah benda di jatuhkan dari pesawat terbang yang melaju horizontal dengan kecepatan 720 km/jam pada ketinggian 490 m. Berapa jauh jautuhnya benda tersebut dari tempat pertama kali pesawat menjatuhkan benda itu?

    (g = 9,8 ms^-2)

a) 2500 m
b) 3000m
c) 1500m
d) 2000m

    Diketahui :  Vo = 720 km/jam
=  720.000m/3600 s
=  200 ms^-1
                           h = 490 m
g = 9,8 ms^-2

Ditanya  :  S = …?

Jawab  :  untuk mencari  jarak (S) maka lebih dulu kita mencari waktu yang diperlukan benda jatuh sampai diatas tanah. Benda itu merupakan benda jatuh bebas, mengapa? Karena kecepatan pesawat 200 ms^-1 arahnya mendatar, sedangkan arah vertical (turun) kecepatannya nol (V_oy = 0)

                    h _turun = y = V_oy.t  + ½ gt²
                    490 m  = 0. t + ½ .9,8 ms^-2. t²
                          t²  = 2. 490 m/ 9,8 ms^-2
                               = 980/9,8 s^-2
                               = 100 s²
                           t   = 10 s

           maka  S = v_ox.t  = Vo.t
= 200 ms^-1. 10 s
= 2000 m

Jadi jawabannya adalah [D]

34. Pada gerak parabola, di titik manakah kelajuan benda paling kecil dan paling besar?

a. Titik terjauh dan titik terdangkal
b. Titik tertinggi dan titik terjauh
c. Titik tertinggi dan titik terdepan
d. Titik terjauh dan titik tertinggi

Jawab:

– Kelajuan terkecil adalah pada titik tertinggi, karena pada titik ini v_y = 0 sehingga v= √v_x²

– Kelajuan terbesar adalah pada titik terjauh.

Jadi jawabannya yang tepat adalah B

35. Perhatikan  faktor-faktor  berikut!
1) Kecepatan awal.
2) Sudut yang dialami benda.
3) Waktu.
4) Percepatan gravitasi.
5) Kecepatan akhir.
Faktor-faktor yang memengaruhi  ketinggian  benda yang mengalami gerak  parabola  ditunjukkan pada nomor…

a. 1), 2), dan 3) saja
b. 1),2),3),  dan 4)
c. 1),2),3),dan 5)
d. 3) dan  5) saja
e. 4) dan 5) saja

Pembahasan

Jawaban :

Faktor-faktor yang memengaruhi  ketinggian  benda yang mengalami gerak  parabola

h = vo sin θ . t – ½ g . t²
vo = kecepatan awal
θ          = sudut elevasi
t           = waktu
g          = percepatan gravitasi

Jadi jawabannya adalah [B]

36. John melempar  batu ke arah horizontal dari sebuah bukit dengan  ketinggian 100 meter. Jika batu  jatuh pada jarak 80 meter dari tempat pelemparan, kecepatan  awal  batu adalah… m/s.

a) 2
b) 4
c) 4√3
d) 4√5
e) 8√5

Pembahasan:

Diketahui
θ = 0^o
x = 80 m

langkah 1

menetukan waktu (t) dengan persamaan:

h          = ½ gt²
t           = √2h/g
=√2.100/10 =√20 = 2√5 sekon

Langkah 2

menetukan kecepatan awal (v_o) dengan persamaan:

X         = v_o cos θ . t
v_o              = x/ cos θ . t
= 80/cos 0^O . 2√5
= 40/√5
= 8 √5 m/s

Jadi jawabannya adalah [E]

37. Gerak parabola dapat dipandang sebagai hasil perpaduan gerak lurus beraturan pada sumbu horizontal (sumbu x) dan gerak lurus berubah beraturan pada sumbu vertical (sumbu y) secara terpisah”.Pendapat ini dikemukakan oleh…

a) Newton
b) Robert Boyle
c) Galileo Galilei
d) Steve Roger

Pembahasan:

Pernyataan tersebut dikemukakan oleh Galileo galilee, sehingga di dapatkan jawaban : C

38. Sebuah parabola yang terbuka keatas melalui titik (3,5) dengan titik fokus (-1, 2). Tentukan koordinat titik puncak parabola.

a. (-1.1)
b. (-1.0)
c. (0,1)
d. (-0.0)

Jarak titik (3, 5) ke fokus = jarak titik (3, 5) ke garis direktriks = 5.
Jadi persamaan garis direktriksnya adalah y = 0
Sehingga titik puncaknya adalah (-1, 1)
Jadi jawabannya adalah A.

39. Sebuah benda dilepaskan dari pesawat terbang yang terbang mendatar dengan kecepatan 40 m/s. Benda dilepaskan dari ketinggian 500 m diatas tanah. Jika  g = 10 m/s², berapakah  (secara berurut ):
1. waktu yang diperlukan benda untuk tiba di tanah
2. Jarak mendatar jatuhnya benda
3. Kecepatan benda sebelum menyentuh tanah;

a. (10 ,400 ,107,7)
b. (10 ,500,208)
c. (10 ,234 ,107,7)
d. (20 ,400, 107,7)

Jawab:

• Gerak vertical benda sama dengan gerak jatuh bebas benda

V₀y   = 0
y       =  gt²
500  =  . 10 .t²
500  = 5t²
t ²     = 100
t       =  10 sekon

• Jarak mendatar diperoleh melalui persamaan :

X  = vx . t
X = (40) .(10)
X  = 400 m

Jadi,jarak mendatar benda 400 m.

• Kecepatan benda sebelum menyentuh tanah dapat dihitung dengan rumus vector resultan kecepatan

Vx  = 40 m/s
Vy  = g .t =(10).(10) = 100 m/s
Vb  =
Vb  =
Vb  = 107,7 m/s

Jadi , kecepatan benda sebelum menyentuh tanah 107,7 m/s. (A)

40. Seseorang memegang bola pada ketinggian 20 meter lalu melempar horisontal ke depan dengan kecepatan awal 5 m/s. Tentukan :
(a) Selang waktu bola tiba di tanah
(b) Jarak horisontal terjauh yang dicapai bola
(c) Kelajuan bola ketika tiba di tanah

Pembahasan
(a) Selang waktu bola tiba di tanah (t)
Penyelesaiannya seperti menentukan selang waktu benda yang melakukan gerak jatuh bebas.

(b) Jarak horisontal terjauh yang dicapai bola (s)
Diketahui :
v_ox = 5 m/s (laju awal pada arah horisontal)
t = 2 sekon (selang waktu bola di udara)
Ditanya : s
Jawab :
v = s / t
s = v t = (5)(2) = 10 meter
(c) Kelajuan bola ketika tiba di tanah (v_t)
v_ox = v_tx = v_x = 5 m/s
v_ty = …. ?
Kelajuan akhir pada arah vertikal dihitung seperti menghitung kelajuan akhir pada gerak jatuh bebas.
Diketahui : v_oy = 0, g = 10, h = 20
Ditanya : v_t
Jawab :

Jadi,jawabannya adalah(2;10;20,6)

41. Sebuah peluru ditembakan dengan kecepatan awal 100 m/s dan sudut elevasi 30⁰. Tentukan:
1. Posisi pada t=1 s
2. kecepatan pada t=1 s
3. Tinggi max yang dicapai peluru
4. Jangkauan terjauh yang dicapai peluru

a) (50√3,45; 50√3,40;125; 500√3)
b) (50√8,56;45√2,22;110;200√3)
c) ( 45√3,45;50√2,40;98;500√3)
d) (35√2,23;35√4,22;125;100√2)

Pembahasan:

1. X = V₀.cos ὰ.t
   = 100.cos 30.1
   = 100.1/2√3.1
   = 50√3 m

   Y = V_o.sin ὰ.t-1/2 gt²
     = 100.sin 30.1-1/2.10.1²
     = 100.1/2.1-1/2.10.1²
     = 45 m

1. V_x= V₀.cos ὰ
   = 100. cos 30
   = 100. 1/2√3
   = 50√3 m/s

   V_y = V₀.sin ὰ-gt
= 100.sin 30-10.1
= 100.1/2-10.1
= 40 m/s

1. Y_max=V_y = 0
   V₀ sin ὰ-gt = 0
   V₀ sin ὰ = gt
   t = V₀.sin ὰ
   ─────────
   g
   = 100.1/2
   ───────── = 5 s

10

Y = V₀ sin ὰ t-1/2 gt²
= 100.1/2.5-1/2.10.5²
= 250-125
= 125 m

1. X_max = y = 0

   V₀ sin ὰ t-1/2 gt² = 0
t = 2.V₀.sin ὰ
───────────
g

     = 2.100.1/2
─────────── = 10 S
10

X  = V₀ cos ὰ t
= 100.1/2√3.10
= 500√3 m

jadi, jawabannya adalah (50√3,45; 50√3,40;125; 500√3) [A]

42. John melakukan servis bola voli dengan kecepatan awal 10m/s. sudut elevasi yang terbentuk sebesar 37ᵒ.kecepatan awal pada sumbu x dan y berturut-turut adalah…

a. 8m/s dan 6 m/s
b. 6m/s dan 8m/s
c. 6m/s dan 6m/s
d. 8m/s dan 8m/s

pembahasan:

t_h= v_o sina

      ────

          g

v_x= v₀ sina
=10sin37ᵒ
=8m/s

V_y=V₀cosa
=10 cos37ᵒ
=6m/s

Jawabannya=A

43. Sebuah peluru yang ditembakkan dengan kecepatan v₀ dan sudut elevasi pada titik tertinggi, maka…

a.tenaga kinetiknya nol
b.tenaga kinetiknya maksimum
c.tenaga potensialnya maksimum
d.tenaga totalnya maksimum

Pembahasan:

 Pada saat titik tertinggi v_y=0 kecepatan peluru=v_x,,maka kecepatan minimum.Energi potensial maksimumdan energi kinetik minimum

Jawabannya=C

44. Sebuah peluru ditembakkan dengan kecepatan awal 100m/s dan sudut elevasi 30ᵒ. Jika gravitasi ditempuh itu 10m/s² ,maka waktu  yang yang diperlukan peluru tersebut untuk mencapai titik tertinggi adalah…

a. 2 Sekon
b. 5 Sekon
c. 6 Sekon
d. 10 Sekon

Pembahasan:

Pada titik tertinggi v_y=0

V₀sin30ᵒ- gt=0

T= v₀sin30ᵒ

      ────

           G

  =100(0,5)/10

  =  5 Sekon

Jawabannya: B

45. Sebuah sasaran terletak pada koordinat (50,8). Seseorang melempar batu dengan sudur elevasi 37⁰, kearah sasaran tersebut dari pusat koordinat, berapa kecepatan yang harus diberikan agar batu dapat tepat mengenai sasaran?

a) 25,73 m/s
b) 27,35 m/s
c) 32,87 m/s
d) 23,45 ms

Penyelesaian : agar sasaran kena maka x = 5 m dan y = 80 m

Diketahui :

y₀ = 0
x₀ = 0
θ = 37⁰
y = 8 m
x = 50 m

Ditanya :

v₀ = … ?

Jawab :

v_0x = v₀ cos 37⁰ = 0,8 v₀
v_0y = v₀ sin 37⁰ = 0,6 v₀
x = x₀ + v_0x . t
50 = 0 + 0,8 v₀ . t
t = 50/0,8 v₀ = 62,5/ v₀
y = y0 + v0y . T . -1/2 . g . t2
8 = 0 + 0,6 v₀ (62,5/ v₀) – 1/2 . 10 . (62,5/ v₀) ²
8 = 37,5 – 5 (3906,25/v₀²)
29,5 = 19531,25/ v₀²
v₀² = 19531,25/29,5
v₀ = √662.08 = 25,73 m/s

Jadi jawabannya adalah [A]

46. Seorang pemain golf, memukul bola dengan kecepatan 6,5 m/s dan sudut elevasi 67,4⁰ , terhadap bidang horizontal.Jika percepatan gravitasi bumi 10 m/s². Tentukanlah secra berurut:
1. waktu yang di butuhkan untuk mencapai titik tejauh
2. ketinggian maksimun yang dapat dicapai
3. jarak terjauh yang dapat dicapai

a) 1 s;2m;4m
b) 1,2 s;1,8m;3m
c) 2s;3m;3,2m
d) 2s;2m;4m

Penyelesaian :

Diketahui :

v₀ = 6,5 m/s
g = 10 m/s
θ = 67,4⁰

Ditanya :

t_0B = …. ?
Y_0H= ….?
X_0B = …. ?

Jawab :

Jadi jawabannya adalah [B]

47. Sebuah peluru ditembakkan dengan kecepatan 50 m/s, dengan sudut elavasiθ. Bila peluru sampai ditanah pada jarak 200 m dari tempat peluru ditembakkan, tentukanlah sudut elevasinya, jika perceptan gravitasi bumi 10 m/s^{2 .}

a) 90ᵒ
b) 45ᵒ
c) 88ᵒ
d) 50ᵒ

Penyelesaian :

Diketahui :

v₀ = 50 m/s
x_0B = 200 m
g = 10 m/s²

Ditanya : θ = … ?

Jawab :

Jadi jawabannya adalah [A]

48. Andy melempar bola basket dengan kecepatan 20 m/s dan sudut elevasi 30^o. Waktu yang dibutuhkan bola basket untuk sampai dititik tertinggi adalah… (g = 10 m/s²)

a) 1 sekon
b) 4 sekon
c) 5 sekon
d) 6 sekon

Pembahasan

Menghitung waktu untuk mencapai ketinggian maksimum:

t = v₀ sin θ / g = 20 m/s sin 30^o / 10 m/s²
t = 20 m/s . (1/2) / (10 m/s²) = 1 sekon

Jawaban: A

49. Benedict menendang bola dengan sudut elevasi 45^o. Bola jatuh dengan jarak mendatar sejauh 5 m. Jika percepatan gravitasi bumi 10 m/s², kecepatan awal bola adalah…

a) 1 m
b) 4 m
c) 6 m
d) 10 m

Pembahasan:

Menghitung kecepatan awal jika jarak terjauh diketahui:

X = v₀² sin 2θ / 2 . g
5 m = v₀² sin 2 . 45^o / (2 . 10 m/s²)
5 m = v₀² . 1 / (20 m/s²)
v₀² = 100 (m/s)²
v₀ = 10 m/s

Jawaban: D

50. Benjamin melempar batu dengan kecepatan 10 m/s dengan sudut elevasi 30^o. Tinggi maksimum yang dicapai batu adalah… (g = 10 m/s²)

a) 1,0 m
b) 1,25 m
c) 2,5 m
d) 3,0 m

Pembahasan:

Menghitung ketinggian maksimum gerak parabola

Yh = v₀² sin² θ / 2 . g = (10 m/s)² sin² 30^o / (2 . 10 m/s²)
Yh = 100 . (1/2)² / 20 m = 25 / 20 m = 5/4 m = 1,25 m

Jawaban: B

Bacaan Lainnya

• Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
• Konstanta Listrik (Permitivitas vakum) – Konstanta Fisika ε0 – Soal dan Jawaban
• Tabel Konstanta Fisika – Tabel konstanta universal, elektromagnetik, atom dan nuklir, fisika-kimia, nilai yang diadopsi, satuan natural, bilangan tetap
• Rumus Gaya Fisika: Gesek, Berat, Relativitas Khusus, Normal, Friksi, Pegas, Elastis dan Konservatif
• Entalpi Termokimia – Pemanasan / Kalor Fisika – Soal dan Jawaban
• Rumus Usaha Fisika – Bersama Contoh Soal dan Jawaban
• Rumus Foton (Kuanta Cahaya) Fisika Contoh Soal dan Jawaban
• Rumus Indeks Bias Bersama Contoh Soal dan Jawaban (Pembiasan Cahaya)
• Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
• Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang
• Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender
• Cara Menghentikan Penindasan Bullying
• Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
• Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
• 10 Cara Memotivasi Anak Untuk Belajar Agar Menjadi Pintar
• Di Indonesia, (HAN) Hari Anak Nasional tanggal 23 Juli
• Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
• Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
• Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
• Sistem Reproduksi Manusia, Hewan dan Tumbuhan
• Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
• Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?