PINTERpandai
Pinter Pandai

Rumus Limit Fungsi Matematika Kalkulus Beserta Contoh Soal dan Jawaban

4 min read

Limit fungsi matematika ini ada pada ketakhinggaan

Limit Fungsi

Limit fungsi atau limit suatu fungsi merupakan salah satu konsep mendasar dalam kalkulus dan analisis, tentang kelakuan suatu fungsi mendekati titik masukan tertentu.

Suatu fungsi memetakan keluaran f(x) untuk setiap masukan x. Fungsi tersebut memiliki limit L pada titik masukan p bila f(x) “dekat” pada L ketika x dekat pada p. Dengan kata lain, f(x) menjadi semakin dekat kepada L ketika x juga mendekat menuju p. Lebih jauh lagi, bila f diterapkan pada tiap masukan yang cukup dekat pada p, hasilnya adalah keluaran yang (secara sembarang) dekat dengan L. Bila masukan yang dekatpada p ternyata dipetakan pada keluaran yang sangat berbeda, fungsi f dikatakan tidak memiliki limit.

Definisi limit dirumuskan secara formal mulai abad ke-19.

 

Definisi Limit Fungsi

Berikut beberapa definisi limit fungsi yang umum diterima.

Fungsi pada garis bilangan riil atau bilangan real

Bila f : R{\displaystyle \rightarrow }R terdefinisi pada garis bilangan riil, dan p, L{\displaystyle \in }R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:

{\displaystyle \lim _{x\to p}f(x)=L}

jika dan hanya jika untuk setiap ε > 0 terdapat δ > 0 sehingga |x – p|< δ mengimplikasikan bahwa |f (x) – L | < ε . Di sini, baik ε maupun δ merupakan bilangan riil. Perhatikan bahwa nilai limit tidak tergantung pada nilai f (p)

Limit searah

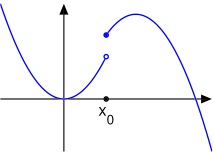
Limit searah - limit fungsi matematika

Limit saat: x → x0+ ≠ x → x0–. Maka, limit x → x0 tidak ada.

Masukan x dapat mendekati p dari atas (kanan di garis bilangan) atau dari bawah (kiri). Dalam hal ini limit masing-masingnya dapat ditulis sebagai

{\displaystyle \lim _{x\to p^{+}}f(x)=L}

atau

{\displaystyle \lim _{x\to p^{-}}f(x)=L}

Bila kedua limit ini sama nilainya dengan L, maka L dapat diacu sebagai limit f(x) pada p . Sebaliknya, bila keduanya tidak bernilai sama dengan L, maka limit f(x) pada p tidak ada.

Definisi formal adalah sebagai berikut. Limit f(x) saat x mendekati p dari atas adalah L bila, untuk setiap ε > 0, terdapat sebuah bilangan δ > 0 sedemikian rupa sehingga |f(x) – L| < ε pada saat 0 < x – p < δ. Limit f(x) saat x mendekati p dari bawah adalah L bila, untuk setiap ε > 0, terdapat bilangan δ > 0 sehingga |f(x) – L| < ε bilamana 0 < p – x < δ.

Bila limitnya tidak ada terdapat osilasi matematis tidak nol.

 

Limit fungsi pada ketakhinggaan

Limit fungsi matematika ini ada pada ketakhinggaan
Limit fungsi matematika ini ada pada ketakhinggaan.

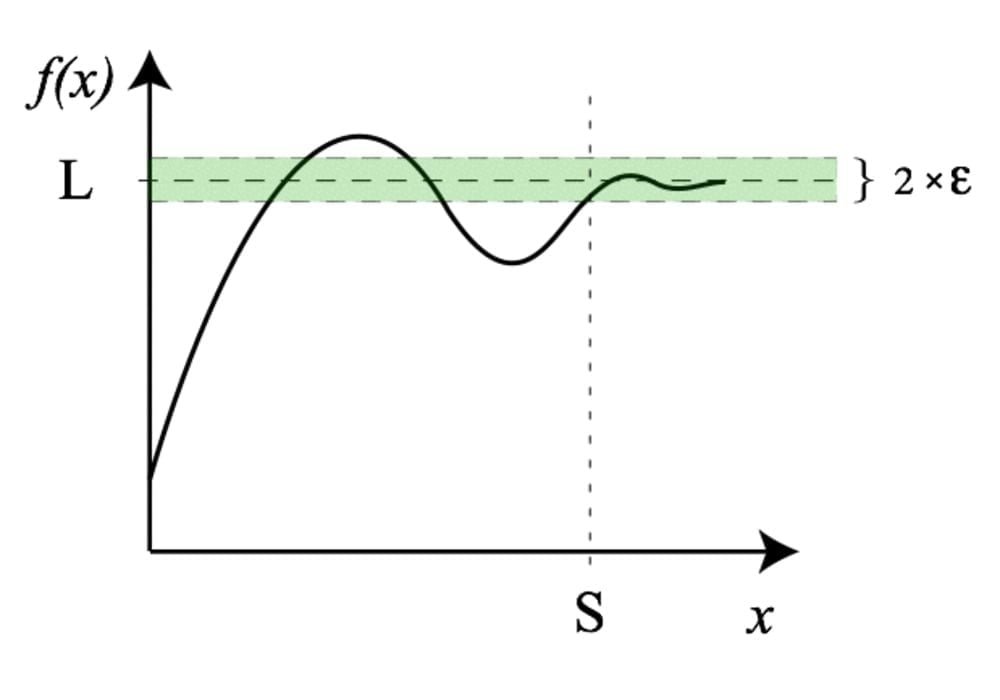
Bila dua unsur, ketakhinggaan positif dan negatif {-∞, +∞}, ditambahkan pada garis bilangan riil, kita dapat mendefinisikan limit fungsi pada ketakhinggaan. Dua unsur tambahan ini bukanlah bilangan, namun berguna dalam memerikan kelakuan limit pada kalkulus dan analisis.

Bila f(x) adalah fungsi riil, maka limit f saat x mendekati tak hingga adalah L, dilambangkan sebagai:

{\displaystyle \lim _{x\to \infty }f(x)=L,}

jika dan hanya jika untuk semua ε > 0 terdapat S > 0 sedemikian rupa sehingga |f (x) – L| < ε bilamana x > S.

Dengan cara yang sama, limit f saat x mendekati tak hingga adalah tak hingga, dilambangkan oleh

{\displaystyle \lim _{x\to \infty }f(x)=\infty ,}

jika dan hanya jika bila untuk semua R > 0 terdapat S > sedemikian sehingga f(x) > R bilamana x > S.

 

Rumus biasa – Limit Fungsi

{\displaystyle {\begin{matrix}\lim \limits _{x\to p}&(f(x)+g(x))&=&\lim \limits _{x\to p}f(x)+\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)-g(x))&=&\lim \limits _{x\to p}f(x)-\lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)\cdot g(x))&=&\lim \limits _{x\to p}f(x)\cdot \lim \limits _{x\to p}g(x)\\\lim \limits _{x\to p}&(f(x)/g(x))&=&{\lim \limits _{x\to p}f(x)/\lim \limits _{x\to p}g(x)}\end{matrix}}}

 

Rumus Limit Fungsi

{\displaystyle {\begin{matrix}\lim \limits _{x\to 0}&{\frac {x}{\sin x}}&=1\\\lim \limits _{x\to 0}&{\frac {\sin x}{x}}&=1\\\lim \limits _{x\to \infty }&x\sin({\frac {1}{x}})&=1\\\lim \limits _{x\to 0}&{\frac {ax}{\sin bx}}&={\frac {a}{b}}\\\lim \limits _{x\to 0}&{\frac {\sin ax}{bx}}&={\frac {a}{b}}\\\lim \limits _{x\to \infty }&{\frac {ax^{m}+b}{px^{n}+q}}&={\frac {a}{p}},\qquad m=n\\\lim \limits _{x\to \infty }&{\sqrt {ax^{2}+bx+c}}-{\sqrt {px^{2}+qx+r}}&={\frac {b-q}{2{\sqrt {a}}}},\qquad a=p\\\lim \limits _{x\to \infty }&(1+{\frac {1}{x}})^{x}&=e\\\lim \limits _{x\to 0}&(1+x)^{\frac {1}{x}}&=e\\\lim \limits _{x\to \infty }&(1+{\frac {a}{x}})^{bx}&=e^{ab}\\\lim \limits _{x\to 0}&(1+ax)^{\frac {b}{x}}&=e^{ab}\\\end{matrix}}}

 

Sejarah Limit Fungsi Matematika

Meskipun termasuk secara implisit dalam pengembangan kalkulus pada abad ke-17 dan 18, gagasan modern limit fungsi baru dibahas oleh Bolzano, yang pada 1817, memperkenalkan dasar-dasar teknik epsilon-delta. Namun karyanya tidak diketahui semasa hidupnya.

Cauchy membahas limit dalam karyanya Cours d’analyse (1821) dan tampaknya telah menyatakan intisari gagasan tersebut, tapi tidak secara sistematis. Presentasi yang ketat terhadap khalayak ramai pertama kali diajukan oleh Weirstrass pada dasawarsa 1850-an dan 1860-an[3], dan sejak itu telah menjadi metode baku untuk menerangkan limit.

Notasi tertulis menggunakan singkatan lim dengan anak panah diperkenalkan oleh Hardy dalam bukunya A Course of Pure Mathematics pada tahun 1908.

 

Contoh Soal dan Jawaban Limit Fungsi

1. Soal: Hitung limit fungsi vektor \displaystyle \lim_{t \to 2} (8ti - t^2j + k)

Penyelesaian:
Dengan metode yang sama seperti limit fungsi pada umumnya, kita langsung mensubstitusikan t = 2 ke fungsi vektornya. Jadi,
\displaystyle \lim_{t \to 2} (8ti - t^2j + k) = (8.2i - (2)^2j + k)
= 16i - 4j + k = (16, -4, 1)
Jadi, fungsi vektor tersebut akan mendekati (16, -4, 1) saat t mendekati 2.

 

 

2. Nilai \displaystyle \lim_{x\to-\infty} \left(2x - \sqrt{4x^2 + 27}\right)=…

Jawaban:

Karena x menuju negatif tak hingga maka, nilai 2x = -\infty  dan \sqrt{4x^2+27} = \infty
Jadi bentuk limitnya -\infty - \infty = - \infty

 

 

3. Jika \displaystyle \lim_{x\to a}\left[f(x)+\frac{1}{g(x)}\right]=4    dan   \displaystyle \lim_{x\to a}\left[f(x)-\frac{1}{g(x)}\right]=-3   maka  \displaystyle \lim_{x\to a}\left[ f(x)g(x)\right]=...

Jawaban:

Dengan menggunakan sifat limit dan menjumlahkan kedua persamaan

\displaystyle \begin{array}{lcrcl} \displaystyle\lim_{x\to a}\left[f(x)+\frac{1}{g(x)}\right]=4&\Leftrightarrow &\displaystyle\lim_{x\to a}f(x)+\lim_{x\to a}\frac{1}{g(x)}&=&4\\ \displaystyle\lim_{x\to a}\left[f(x)-\frac{1}{g(x)}\right]=-3&\Leftrightarrow &\displaystyle\lim_{x\to a}f(x)-\lim_{x\to a}\frac{1}{g(x)}&=&-3~~~~~+\\ \hline &&\displaystyle 2\lim_{x\to a}f(x)&=&1\\ &&\displaystyle \therefore\:\lim_{x\to a}f(x)&=&\dfrac{1}{2} \end{array}

Subtitusi ke persamaan sebelumnya akan didapat nilai \displaystyle \lim_{x\to a}\frac{1}{g(x)}=\frac{7}{2}~\rightarrow~\lim_{x\to a}g(x)=\frac{2}{7} .

Jadi \displaystyle \lim_{x\to a}\left[ f(x)\cdot g(x)\right]=\lim_{x\to a} f(x)\cdot \lim_{x\to a}g(x)=\frac{2}{14}

Jawaban : B

catatan :

\boxed{~\lim_{x\to a} \left[f(x)\pm g(x)\right]=\lim_{x\to a} f(x)\pm \lim_{x\to a}g(x)~}

\boxed{~\lim_{x\to a} \left[f(x)\cdot g(x)\right]=\lim_{x\to a} f(x)\cdot \lim_{x\to a}g(x)~}

 

 

4. Soal: Jika \lim_{x \to 4} \frac{ax+b-\sqrt{x}}{x-4}=\frac{3}{4} maka a + b sama dengan…

Jawaban:

Limit fungsi di ruas kiri ada, padahal nilai penyebut untuk x = 4 bernilai 0, sehingga pembilangnya bernilai 0 juga.

\begin{aligned} ax+b-\sqrt{x} &= 0 \\ 4a+b-\sqrt{4} &= 0 \\ 4a+b &= 2 \qquad ... \, (1) \end{aligned}

Dengan menggunakan dalil L’Hospital

\begin{aligned} \lim_{x \to 4} \frac{ ax+b-\sqrt{x} }{x-4} &= \frac{3}{4} \\ \lim_{x \to 4} \frac{ a-\frac{1}{2} x^{-\frac{1}{2}} }{1} &= \frac{3}{4} \qquad \text{(dalil L'Hospital)} \\ a-\frac{1}{2} (4)^{-\frac{1}{2}} &= \frac{3}{4} \\ \therefore \: a &=1 \end{aligned}

Subtitusi nial a ke persamaan (1) diperoleh b = -2, sehingga a + b = -1

 

 

5. Nilai \displaystyle \lim_{x\to\frac{\pi}{4}} \sin\left(\frac{\pi}{4}-x\right)\tan\left(x+\frac{\pi}{4}\right) adalah…

Jawaban:

\displaystyle \begin{aligned} &\lim_{x\to\frac{\pi}{4}} \sin\left(\frac{\pi}{4}-x\right)\tan\left(x+\frac{\pi}{4}\right)\\ &=\lim_{x-\frac{\pi}{4}\to 0} \sin\left(\frac{\pi}{4}-x\right)\cdot\tan\left\{\left(x-\frac{\pi}{4}\right)+\frac{\pi}{2}\right\}&~~~~~\left[ \text{mis: }p=x-\frac{\pi}{4}\right ]\\ &=\lim_{p\to 0} \:\sin(-p)\cdot\tan\left(p+\frac{\pi}{2}\right)\\ &=\lim_{p\to 0} \:\sin(-p)\cdot\cot(-p)\\ &=\lim_{p\to 0} \frac{-\sin{p}}{-\tan{p}}\\ &=1 \end{aligned}

catatan:

\boxed{~\tan\left(x+\dfrac{\pi}{2}\right)=-\cot x~}

\boxed{~\sin(-x)=-\sin x~}

 

 

6. Soal:  \displaystyle\lim_{x\to\infty}\left(5^x+5^{3x}\right)^{\frac{1}{x}}=....

Jawaban:

\displaystyle \begin{aligned} \lim_{x\to\infty}\left(5^x+125^{x}\right)^{\frac{1}{x}} &=\lim_{x\to\infty}\exp{\left\{\ln\left(5^x+125^{x}\right)^{\frac{1}{x}}\right\}}\\ &=\exp\left\{\lim_{x\to\infty} \frac{\ln\left(5^x+125^{x}\right)}{x}\right\}&\text{(gunakan dalil L'Hospital)}\\ &=\exp\left\{\lim_{x\to\infty} \frac{5^x\ln(5)+125^x\ln(125)}{5^x+125^{x}}\right \}\\ &=\exp\left\{\lim_{x\to\infty} \frac{5^x(\ln(5)+25^x\ln(125))}{5^x(1+25^{x})}\right \}\\ &=\exp\left\{\lim_{x\to\infty} \frac{\ln(5)+25^x\ln(125)}{1+25^{x}} \times\frac{\frac{1}{25^x}}{\frac{1}{25^x}}\right\}\\ &=\exp\left\{\lim_{x\to\infty} \frac{\frac{\ln(5)}{25^x}+\ln(125)}{\frac{1}{25^x}+1} \times\frac{\frac{1}{25^x}}{\frac{1}{25^x}}\right\}\\ &=\exp(\ln125)\\ &=125 \end{aligned}

Cara Alternatif: :

Jawaban : E

catatan :

\boxed{~\ln(a^n)=n\cdot\ln(a)~}

\boxed{~x=e^{\ln{x}}=\exp(\ln{x})~}

Dalil L’Hospital, untuk limit yang berbentuk 0/0 atau \frac{\infty}{\infty}
\boxed{~\lim_{x\to\infty}\frac{f(x)}{g(x)}=\lim_{x\to\infty}\frac{f'(x)}{g'(x)}~}

\boxed{~y=a^x\:\rightarrow\:y'=a^x\cdot\ln(a)~}

\boxed{~y=\ln\left(f(x)\right)\:\rightarrow\:y'=\frac{f'(x)}{f(x)}~}

\boxed{~a^m\cdot a^n=a^{m+n}~}

\boxed{~\lim_{x\to\infty}\frac{1}{x}=0~}

 

 

7. Nilai \displaystyle \lim_{x\to 2}\left(\frac{6}{x^2-x-2}-\frac{2}{x-2}\right) sama dengan…

Jawaban:

Bentuk limit tak tentu \infty-\infty. Lakukan sedikit modifikasi:

\displaystyle \begin{aligned} \lim_{x\to 2}\left\{\frac{6}{x^2-x-2}-\frac{2}{x-2}\right\} &=\lim_{x\to 2}\left\{\frac{6}{(x-2)(x+1)}-\frac{2}{x-2}\right\}\\ &=\lim_{x\to 2}\left\{\frac{6}{(x-2)(x+1)}-\frac{2(x+1)}{(x-2)(x+1)}\right\}\\ &=\lim_{x\to 2}\frac{2(2-x)}{(x-2)(x+1)}\\ &=\lim_{x\to 2}\frac{-2}{(x+1)}\\ &=-\frac{2}{3} \end{aligned}

 

 

8. Nilai \displaystyle \lim_{x\to 0} \frac{1-\cos^2\!{x}}{x^2\cdot\cot\left(x+\frac{\pi}{3}\right)}=...

Jawaban:

\displaystyle \begin{aligned} \lim_{x\to 0} \frac{1-\cos^2\!{x}}{x^2\cdot\cot\left(x+\frac{\pi}{3}\right)} &=\lim_{x\to 0} \frac{\sin^2\!{x}}{x^2\cdot\cot\left(x+\frac{\pi}{3}\right)}\\ &=\lim_{x\to 0} \left(\frac{\sin{x}}{x}\cdot\frac{\sin{x}}{x}\cdot\tan\left(x+\frac{\pi}{3}\right) \right)\\ &=(1)(1)(\sqrt{3})\\ &=\sqrt{3} \end{aligned}

 
 
 

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

 

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

                      

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya


Pinter Pandai
«
»

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

PinterPandai
Okt 14, 2024 58 sec read

Tes matematika logika: Jika 4 + 3 = 27,…

PinterPandai
Okt 9, 2024 1 min read

Nilai Pi 1 juta digit pertama | Analisis dan…

PinterPandai
Mei 8, 2024 1 min read

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *