Kalkulus

Adalah cabang ilmu matematika yang mencakup limit, turunan, integral dan deret takterhingga. Kalkulus adalah ilmu yang mempelajari perubahan, sebagaimana geometri yang mempelajari bentuk dan aljabar yang mempelajari operasi dan penerapannya untuk memecahkan persamaan. Rumus Kalkulus memiliki aplikasi yang luas dalam bidang-bidang sains, ekonomi dan teknik; juga dapat memecahkan berbagai masalah yang tidak dapat dipecahkan dengan aljabar elementer.

Prinsip-prinsip dasar Kalkulus dan Rumus Kalkulus

1. Limit dan kecil tak terhingga Kalkulus

Definisi limit: dapat dikatakan bahwa limit f(x) ketika x mendekati titik p adalah L apabila untuk setiap bilangan ε > 0 apapun, terdapat bilangan δ > 0, sedemikian rupanya:

0<|x-p|<\delta \Rightarrow |f(x)-L|<\epsilon

Pada umumnya rumus Kalkulus dikembangkan dengan memanipulasi sejumlah kuantitas yang sangat kecil. Objek ini, yang dapat diperlakukan sebagai angka, adalah sangat kecil. Sebuah bilangan dx yang kecilnya tak terhingga dapat lebih besar daripada 0, namun lebih kecil daripada bilangan apapun pada deret 1, ½, ⅓, … dan bilangan real positif apapun. Setiap perkalian dengan kecil tak terhingga (infinitesimal) tetaplah kecil tak terhingga, dengan kata lain kecil tak terhingga tidak memenuhi “ciri-ciri Archimedes”. Dari sudut pandang ini, kalkulus adalah sekumpulan teknik untuk memanipulasi kecil tak terhingga.

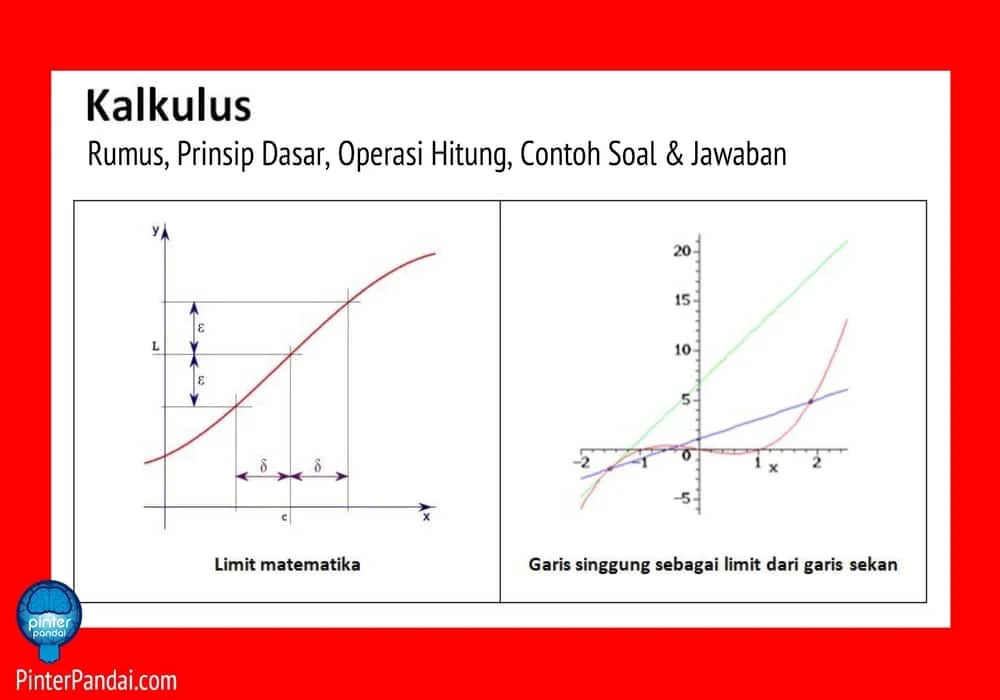
Pada abad ke-19, konsep kecil tak terhingga ini ditinggalkan karena tidak cukup cermat, sebaliknya ia digantikan oleh konsep limit. Limit menjelaskan nilai suatu fungsi pada nilai input tertentu dengan hasil dari nilai input terdekat. Dari sudut pandang ini, rumus kalkulus adalah sekumpulan teknik memanipulasi limit-limit tertentu. Secara cermat, definisi limit suatu fungsi adalah:

Diberikan fungsi f(x) yang terdefinisikan pada interval di sekitar p, terkecuali mungkin pada p itu sendiri. Kita mengatakan bahwa limit f(x) ketika x mendekati p adalah L, dan menuliskan:
$\lim _{x\to p}{f(x)}=L$
jika, untuk setiap bilangan ε > 0, terdapat bilangan δ > 0 yang berkoresponden dengannya sedemikian rupanya untuk setiap x:
$0<|x-p|<\delta \Rightarrow |f(x)-L|<\epsilon \,$

2. Turunan Rumus Kalkulus

Turunan dari suatu fungsi mewakili perubahan yang sangat kecil dari fungsi tersebut terhadap variabelnya. Proses menemukan turunan dari suatu fungsi disebut sebagai pendiferensialan ataupun diferensiasi.

Secara matematis, turunan fungsi ƒ(x) terhadap variabel x adalah ƒ′ yang nilainya pada titik x adalah:

f'(x)=\lim _{h\to 0}{f(x+h)-f(x) \over {h}}

dengan syarat limit tersebut eksis. Jika ƒ′ eksis pada titik x tertentu, kita katakan bahwa ƒ terdiferensialkan (memiliki turunan) pada x, dan jika ƒ′ eksis di setiap titik pada domain ƒ, kita sebut ƒ terdiferensialkan.

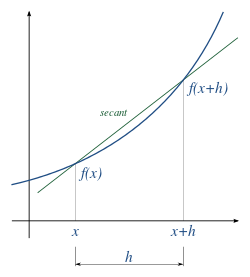
Apabila z = x + h, h = z – x, dan h mendekati 0 jika dan hanya jika z mendekati x, maka definisi turunan di atas dapat pula kita tulis sebagai:

f'(x)=\lim _{z\to x}{f(z)-f(x) \over {z-x}}

Garis singgung pada (x, f(x)). Turunan f’(x) sebuah kurva pada sebuah titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut.

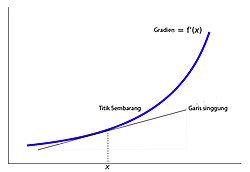
Perhatikan bahwa ekspresi ${f(x+h)-f(x) \over {h}}$ pada definisi turunan di atas merupakan gradien dari garis sekan yang melewati titik (x,ƒ(x)) dan (x+h,ƒ(x)) pada kurva ƒ(x). Apabila kita mengambil limit h mendekati 0, maka kita akan mendapatkan kemiringan dari garis singgung yang menyinggung kurva ƒ(x) pada titik x.

Hal ini berarti pula garis singgung suatu kurva merupakan limit dari garis sekan, demikian pulanya turunan dari suatu fungsi ƒ(x) merupakan gradien dari fungsi tersebut. Klik disini untuk membaca lebih lanjut tentang Rumus Kalkulus: Rumus Turunan Matematika – TABEL TURUNAN DIFERENSIAL

Sebagai contoh, untuk menemukan gradien dari fungsi $f(x)=x^{2}$ pada titik (3,9):

{\begin{aligned}f'(3)&=\lim _{h\to 0}{(3+h)^{2}-9 \over {h}}\\&=\lim _{h\to 0}{9+6h+h^{2}-9 \over {h}}\\&=\lim _{h\to 0}{6h+h^{2} \over {h}}\\&=\lim _{h\to 0}(6+h)\\&=6\end{aligned}}

Ilmu yang mempelajari definisi, properti dan aplikasi dari turunan atau kemiringan dari sebuah grafik disebut kalkulus diferensial.

Garis singgung sebagai limit dari garis sekan. Turunan dari kurva f(x) di suatu titik adalah kemiringan dari garis singgung yang menyinggung kurva pada titik tersebut. Kemiringan ini ditentukan dengan memakai nilai limit dari kemiringan garis sekan.

Notasi pendiferensialan

Terdapat berbagai macam notasi matematika yang dapat digunakan untuk menyatakan turunan, meliputi notasi Leibniz, notasi Lagrange, notasi Newton dan notasi Euler.

Notasi Leibniz diperkenalkan oleh Gottfried Leibniz dan merupakan salah satu notasi yang paling awal digunakan. Ia sering digunakan terutama ketika hubungan antar y = ƒ(x) dipandang sebagai hubungan fungsional antara variabel bebas dengan variabel terikat. Turunan dari fungsi rumus kalkulus tersebut terhadap x ditulis sebagai:

{\frac {dy}{dx}},\quad {\frac {df}{dx}}(x),

ataupun

{\frac {d}{dx}}f(x).

Notasi Lagrange diperkenalkan oleh Joseph Louis Lagrange dan merupakan notasi yang paling sering digunakan. Dalam notasi ini, turunan fungsi ƒ(x) ditulis sebagai ƒ′(x) ataupun hanya ƒ′.

Notasi Newton, juga disebut sebagai notasi titik, menempatkan titik di atas fungsi untuk menandakan turunan. Apabila y = ƒ(t), maka ${\dot {y}}$ mewakili turunan y terhadap t. Notasi ini hampir secara eksklusif digunakan untuk melambangkan turunan terhadap waktu. Notasi ini sering terlihat dalam bidang fisika dan bidang matematika yang berhubungan dengan fisika.

Notasi Euler menggunakan operator diferensial D yang diterapkan pada fungsi ƒ untuk memberikan turunan pertamanya Df. Apabila y = ƒ(x) adalah variabel terikat, maka sering kali x dilekatkan pada D untuk mengklarifikasikan keterbebasan variabel x. Notasi Euler kemudian ditulis sebagai:

D_{x}f(x)\,

Notasi Euler ini sering digunakan dalam menyelesaikan persamaan diferensial linear.

	Notasi Leibniz	Notasi Lagrange	Notasi Newton	Notasi Euler
Turunan ƒ(x) terhadap x	${\frac {d}{dx}}f(x)$	ƒ′(x)	${\dot {y}}$ dengan y = ƒ(x)	$D_{x}f(x)\,$

3. Integral

Integral dapat dianggap sebagai perhitungan luas daerah di bawah kurva ƒ(x), antara dua titik a dan b.

Integral merupakan suatu objek matematika yang dapat diinterpretasikan sebagai luas wilayah ataupun generalisasi suatu wilayah. Proses menemukan integral suatu fungsi disebut sebagai pengintegralan ataupun integrasi. Dalam rumus kalkulus, Integral dibagi menjadi 2, yaitu: integral tertentu dan integral tak tentu. Notasi matematika yang digunakan untuk menyatakan integral adalah $\int \,$ , seperti huruf S yang memanjang (S singkatan dari “Sum” yang berarti penjumlahan).

Integral tertentu

Diberikan suatu fungsi ƒ bervariabel real x dan interval antara [a, b] pada garis real, integral tertentu:

\int _{a}^{b}f(x)\,dx\,,

secara informal didefinisikan sebagai luas wilayah pada bidang xy yang dibatasi oleh kurva grafik ƒ, sumbu-x, dan garis vertikal x = a dan x = b.

Pada notasi integral di atas: a adalah batas bawah dan b adalah batas atas yang menentukan domain pengintegralan, ƒ adalah integran yang akan dievaluasi terhadap xpada interval [a,b], dan dx adalah variabel pengintegralan.

Seiring dengan semakin banyaknya subinterval dan semakin sempitnya lebar subinterval yang diambil, luas keseluruhan batangan akan semakin mendekati luas daerah di bawah kurva.

Terdapat berbagai jenis pendefinisian formal integral tertentu, namun yang paling umumnya digunakan adalah definisi integral Riemann. Integral Rieman didefinisikan sebagai limit dari “penjumlahan Riemann”.

Misalkanlah kita hendak mencari luas daerah yang dibatasi oleh fungsi ƒ pada interval tertutup [a,b]. Dalam mencari luas daerah tersebut, interval [a,b] dapat kita bagi menjadi banyak subinterval yang lebarnya tidak perlu sama, dan kita memilih sejumlah n-1 titik {x₁, x₂, x₃,…, x_{n – 1}} antara a dengan b sehingga memenuhi hubungan:

a=x_{0}\leq x_{1}\leq x_{2}\leq \cdots \leq x_{n-1}\leq x_{n}=b.\,\!

Himpunan $P=\{x_{0},x_{1},x_{2},\ldots ,x_{n-1},x_{n}\}\,$ tersebut kita sebut sebagai partisi [a,b], yang membagi [a,b] menjadi sejumlah n subinterval $[x_{0},x_{1}],[x_{1},x_{2}],\ldots ,[x_{n-1},x_{n}]$ . Lebar subinterval pertama [x₀,x₁] kita nyatakan sebagai Δx₁, demikian pula lebar subinterval ke-i kita nyatakan sebagai Δx_i = x_i – x_{i – 1}. Pada tiap-tiap subinterval inilah kita pilih suatu titik sembarang dan pada subinterval ke-i tersebut kita memilih titik sembarang t_i. Maka pada tiap-tiap subinterval akan terdapat batangan persegi panjang yang lebarnya sebesar Δx dan tingginya berawal dari sumbu x sampai menyentuh titik (t_i, ƒ(t_i)) pada kurva. Apabila kita menghitung luas tiap-tiap batangan tersebut dengan mengalikan ƒ(t_i)· Δx_i dan menjumlahkan keseluruhan luas daerah batangan tersebut, kita akan dapatkan:

S_{p}=\sum _{i=1}^{n}f(t_{i})\Delta x_{i}

Penjumlahan S_p disebut sebagai penjumlahan Riemann untuk ƒ pada interval [a,b]. Perhatikan bahwa semakin kecil subinterval partisi yang kita ambil, hasil penjumlahan Riemann ini akan semakin mendekati nilai luas daerah yang kita inginkan. Apabila kita mengambil limit dari norma partisi $\lVert P\rVert$ mendekati nol, maka kita akan mendapatkan luas daerah tersebut.

Secara cermat, definisi integral tertentu sebagai limit dari rumus kalkulus penjumlahan Riemann adalah:

Diberikan ƒ(x) sebagai fungsi yang terdefinisikan pada interval tertutup [a,b]. Kita katakan bahwa bilangan I adalah integral tertentu ƒ di sepanjang [a,b] dan bahwa I adalah limit dari penjumlahan Riemann $\sum _{i=1}^{n}f(t_{i})\Delta x_{i}$ apabila kondisi berikut dipenuhi: Untuk setiap bilangan ε > 0 apapun terdapat sebuah bilangan δ > 0 yang berkorespondensi dengannya sedemikian rupanya untuk setiap partisi $P=\{x_{0},x_{1},\ldots ,x_{n}\}$ di sepanjang [a,b] dengan $\lVert P\rVert <\delta$ dan pilihan t_i apapun pada [x_{k – 1}, t_i], kita dapatkan
$\left|\sum _{i=1}^{n}f(t_{i})\Delta x_{i}-I\right|<\epsilon .$

Secara matematis dapat ditulis:

\lim _{\lVert P\rVert \to 0}\sum _{i=1}^{n}f(t_{i})\Delta x_{i}=I=\int _{a}^{b}f(x)\,dx

Apabila tiap-tiap partisi mempunyai sejumlah n subinterval yang sama, maka lebar Δx = (b–a)/n, sehingga persamaan di atas dapat pula ditulis sebagai:

\lim _{n\to \infty }\sum _{i=1}^{n}f(t_{i})\Delta x=I=\int _{a}^{b}f(x)\,dx

Limit ini selalu diambil ketika norma partisi mendekati nol dan jumlah subinterval yang ada mendekati tak terhingga banyaknya.

Contoh

Sebagai contohnya, apabila hendak menghitung integral tertentu $\int _{0}^{b}x\,dx$ , yakni mencari luas daerah A di bawah kurva y=x pada interval [0,b], b>0, maka perhitungan integral tertentu $\int _{0}^{b}x\,dx$ sebagai limit dari penjumlahan Riemannnya adalah $\lim _{\lVert P\rVert \to 0}\sum _{i=1}^{n}f(t_{i})\Delta x_{i}$

Pemilihan partisi ataupun titik t_i secara sembarang akan menghasilkan nilai yang sama sepanjang norma partisi tersebut mendekati nol. Apabila kita memilih partisi P membagi-bagi interval [0,b] menjadi n subinterval yang berlebar sama Δx = (b – 0)/n = b/n dan titik t’_i yang dipilih adalah titik akhir kiri setiap subinterval, partisi yang kita dapatkan adalah:

P=\{0,{\frac {b}{n}},{\frac {2b}{n}},{\frac {3b}{n}},\ldots ,{\frac {nb}{n}}\}

dan

t_{i}={\frac {ib}{n}}

, sehingga:

{\begin{aligned}\int _{0}^{b}f(x)\,dx&=\lim _{n\to \infty }\sum _{i=1}^{n}f(t_{i})\Delta x\\&=\lim _{n\to \infty }\sum _{i=1}^{n}{\frac {ib}{n}}.{\frac {b}{n}}\\&=\lim _{n\to \infty }\sum _{i=1}^{n}{\frac {ib^{2}}{n^{2}}}\\&=\lim _{n\to \infty }{\frac {b^{2}}{n^{2}}}\sum _{i=1}^{n}i\\&=\lim _{n\to \infty }{\frac {b^{2}}{n^{2}}}.{\frac {n(n+1)}{2}}\\&=\lim _{n\to \infty }{\frac {b^{2}}{2}}(1+{\frac {1}{n}})\\\end{aligned}}

Seiring dengan n mendekati tak terhingga dan norma partisi $\lVert P\rVert$ mendekati 0, maka didapatkan:

\int _{0}^{b}f(x)\,dx=A={\frac {b^{2}}{2}}

Dalam praktiknya, penerapan definisi integral tertentu dalam mencari nilai integral tertentu tersebut jarang sekali digunakan karena tidak praktis. Teorema dasar rumus kalkulus (lihat bagian bawah) memberikan cara yang lebih praktis dalam mencari nilai integral tertentu.

Integral tak tentu

Manakala integral tertentu adalah sebuah bilangan yang besarnya ditentukan dengan mengambil limit penjumlahan Riemann, yang diasosiasikan dengan partisi interval tertutup yang norma partisinya mendekati nol, teorema dasar rumus kalkulus (lihat bagian bawah) menyatakan bahwa integral tertentu sebuah fungsi kontinu dapat dihitung dengan mudah apabila kita dapat mencari antiturunan/antiderivatif fungsi tersebut.

Apabila
$F'\!(x)={\frac {d}{dx}}F(x)=f(x).$
Keseluruhan himpunan antiturunan/antiderivatif sebuah fungsi ƒ adalah integral tak tentu ataupun primitif dari ƒ terhadap x dan dituliskan secara matematis sebagai:
$\int f(x)dx=F(x)+C$

Ekspresi F(x) + C adalah antiderivatif umum ƒ dan C adalah konstanta sembarang.

Misalkan terdapat sebuah fungsi $f(x)=x^{2}$ , maka integral tak tentu ataupun antiturunan dari fungsi tersebut adalah:

\int x^{2}dx={\frac {1}{3}}x^{3}+C

Perhatikan bahwa rumus kalkulus integral tertentu berbeda dengan integral tak tentu. Integral tertentu dalam bentuk $\int _{a}^{b}f(x)dx$ adalah sebuah bilangan, manakala integral tak tentu: $\int f(x)dx$ adalah sebuah fungsi yang memiliki tambahan konstanta sembarang C.

4. Teorema dasar kalkulus

Teorema dasar rumus kalkulus menyatakan bahwa turunan dan integral adalah 2 operasi yang saling berlawanan. Lebih tepatnya, teorema ini menghubungkan nilai dari anti derivatif dengan integral tertentu. Karena lebih mudah menghitung sebuah anti derivatif daripada menerapkan definisi integral tertentu, teorema dasar kalkulus memberikan cara yang praktis dalam menghitung integral tertentu.

Teorema dasar kalkulus menyatakan:

Jika sebuah fungsi f adalah kontinu pada interval [a,b] dan jika F adalah fungsi yang mana turunannya adalah f pada interval (a,b), maka
$\int _{a}^{b}f(x)\,dx=F(b)-F(a).$
Lebih lanjut, untuk setiap x di interval (a,b),
$F'(x)={\frac {d}{dx}}\int _{a}^{x}f(t)\,dt=f(x).$

Sebagai contohnya apabila kita hendak menghitung nilai integral $\int _{a}^{b}x\,dx$ , daripada menggunakan definisi integral tertentu sebagai limit dari penjumlahan Riemann (lihat bagian atas), kita dapat menggunakan teorema dasar kalkulus dalam menghitung nilai integral tersebut.

Anti derivatif dari fungsi $f(x)=x\,$ adalah $F(x)={\frac {1}{2}}x^{2}+C$ . Oleh sebab itu, sesuai dengan teorema dasar rumus kalkulus, nilai dari integral tertentu $\int _{a}^{b}x\,dx$ adalah:

{\begin{aligned}\int _{a}^{b}x\,dx&=F(b)-F(a)\\&={\frac {1}{2}}b^{2}-{\frac {1}{2}}a^{2}\\\end{aligned}}

Apabila kita hendak mencari luas daerah A dibawah kurva y=x pada interval [0,b], b>0, maka kita akan dapatkan:

\int _{0}^{b}x\,dx={\frac {b^{2}}{2}}

Perhatikan bahwa hasil yang kita dapatkan dengan menggunakan teorema dasar kalkulus ini adalah sama dengan hasil yang kita dapatkan dengan menerapkan definisi integral tertentu (lihat bagian atas). Oleh karena lebih praktis, teorema dasar rumus kalkulus sering digunakan untuk mencari nilai integral tertentu.

Untuk membaca lebih lanjut tentang teorema dasar kalkulus, mohon klik disini.

Apa gunanya kalkulus?

Pola spiral logaritma cangkang Nautilus adalah contoh klasik untuk menggambarkan perkembangan dan perubahan yang berkaitan dengan kalkulus.

Kalkulus digunakan di setiap cabang sains fisik, sains komputer, statistika, teknik, ekonomi, bisnis, kedokteran, kependudukan dan di bidang-bidang lainnya.
Setiap konsep di mekanika klasik saling berhubungan melalui kalkulus. Massa dari sebuah benda dengan massa jenis yang tidak diketahui, momen inersia dari suatu objek, dan total energi dari sebuah objek dapat ditentukan dengan menggunakan kalkulus.
Dalam subdisiplin listrik dan magnetisme, kalkulus dapat digunakan untuk mencari total aliran (fluks) dari sebuah medan elektromagnetik.
Contoh historis lainnya adalah penggunaan kalkulus di hukum gerak Newton, dinyatakan sebagai laju perubahan yang merujuk pada turunan: Laju perubahan momentum dari sebuah benda adalah sama dengan resultan gaya yang bekerja pada benda tersebut dengan arah yang sama.
Bahkan rumus umum dari hukum kedua Newton: Gaya = Massa × Percepatan, menggunakan perumusan kalkulus diferensial karena percepatan bisa dinyatakan sebagai turunan dari kecepatan. Teori elektromagnetik Maxwell dan teori relativitas Einstein juga dirumuskan menggunakan rumus kalkulus diferensial.

Contoh soal dan jawaban Kalkulus

1. Jika f (x) = g (u) dan u = u (x) lalu

(A) f ‘(x) = g’ (u)
(B) f ‘(x) = g’ (u). u ‘(x)
(C) f ‘(x) = u’ (x)
(D) Tidak ada di atas

Jawaban:
(B). Turunan dari komposisi dua fungsi diberikan oleh aturan rantai.

2. Soal: 2x-7<4x-2

Jawab :
2x-4x<-2+7
-2x<5
x>-5/2
HP (-5/~)
HP {x|x>-5/2,XER}

3. Soal: x-7>2x-5

Jawaban:
x-2x>-5+7
-x>2
x>-2
HP (-2,~)
HP {x|x-2,XER}

4. x2+2x-12<0

Jawaban:
x2+2x-12<0 (x nya dihilangkan 1)
x+2<0
x=-2
HP (-~,-2)
HP {x|x-2,XER}
ATAU
x2+2x-12<0 (x nya dihilangkan 1)
x+2<12
x<10
HP (-~,10)
HP {x|x<10,XER}

5. Biaya marginal suatu perusahaan ditunjukkan oleh MC = 4Q² – 3Q + 5, dengan Q = banyak unit dan biaya tetap k = 3, k adalah konstanta integral. Tentukan persamaan biaya total (C).

Jawaban & pembahasan :
Fungsi biaya marginal MC = 4Q² – 3Q + 5.
MC = dC / dQ = dengan kata lain dC = MC dQ
C = ʃ MC dQ
= ʃ (4Q² – 3Q + 5) dQ
= 4/3 Q³ – 3/2 Q² + 5Q + k
Oleh karena itu, C = 4/3 Q³ – 3/2 Q² + 5Q + k

6. Tentukan hasil integral fungsi-fungsi berikut.
a. ʃ 5 dx
b. ʃ 4x⁵ dx
c. ʃ2 dx

Jawaban & pembahasan:

a. ʃ 5 dx = 5 ʃ dx = 5x + c

b. ʃ 4x⁵ dx = 4 ʃ x⁵ dx = x⁵ + 1 + c = x⁶ + c = x⁶ +c

c. ʃ 2 dx = 2 ʃx dx = + c = + c = + c

7. Selesaikan setiap pengintegralan berikut:
a. ʃ x⁴ dx
b. ʃ (x + 3)² dx

Jawaban:

a. ʃ x4 dx = ʃ x⁴ . x^1/2 dx = ʃ dx = dx + c = + c

b. ʃ (x + 3)² dx = ʃ (x² + 6x + 9) dx = x³ + 3x²+ 9x + c

8. Diketahui turunan dari y = f(x) adalah = f ‘(x) = 2x + 3.
Jika kurva y = f(x) melalui titik (1, 6), tentukan persamaan kurva tersebut.

Jawaban :
Diketahui f ‘(x) = 2x + 3.
Dengan demikian, y = f(x) = ʃ (2x + 3) dx = x² + 3x + c.
Kurva melalui titik (1, 6), berarti f(1) = 6 sehingga dapat kita tentukan nilai c, yaitu 1 + 3 + c = 6 ↔ c = 2.
Jadi, persamaan kurva yang dimaksud adalah y = f(x) = x² + 3x + 2.

9. Biaya marginal suatu perusahaan ditunjukkan oleh MC = 4Q² – 3Q + 5, dengan Q = banyak unit dan biaya tetap k = 3, k adalah konstanta integral. Tentukan persamaan biaya total (C).

Pembahasan & jawaban:
Fungsi biaya marginal MC = 4Q² – 3Q + 5.
MC = dC / dQ = dengan kata lain dC = MC dQ
C = ʃ MC dQ
= ʃ (4Q² – 3Q + 5) dQ
= 4/3 Q³ – 3/2 Q² + 5Q + k
Oleh karena itu, C = 4/3 Q³ – 3/2 Q² + 5Q + k

10. Tentukan hasil integral berikut.
a. ʃ (2x + 6)(x2 + 6x + 3)7 dx
b. ʃ (x2 – 8x + 1)(x – 4)dx

Pembahasan:
a. ʃ (2x + 6)(x2 + 6x + 3)7 dx = ʃ (x2 + 6x + 3)7 (2x + 6) dx

Cara 1:
Misalkan u = x2 + 6x + 3 ↔ du/dx = 2x + 6
↔ du = (2x + 6) dx.
Oleh karena itu,
ʃ (x2 + 6x + 3)7 (2x + 6) dx= ʃ u7 du
= 1/8 u8 + c
= 1/8 (x2 + 6x + 3)8 + c

Cara 2:
ʃ (2x + 6)(x2 + 6x + 3)7 dx = ʃ (x2 + 6x +3)7 d (x2 + 6x + 3)
= 1/8 (x2 + 6x + 3)8 + c

b. ʃ (x2 – 8x + 1)(x – 4) dx

Cara 1:
Misalkan u = x2 – 8x + 1.
du/dx = 2x – 8 ↔ 1/2 du = (x – 4) dx
Oleh karena itu,
ʃ (x2 – 8x + 1)(x – 4)dx = u. ½ du = ½ ʃ u du = ½ (1/2 u2) + c = ¼ u2 + c = ¼ (x2 – 8x + 1)2 + c

Cara 2:
ʃ (x2 – 8x + 1)(x – 4)dx
= ʃ (x2 – 8x + 1) ½ d (x2 – 8x + 1)
= ½ ʃ (x2 – 8x + 1) d(x2 – 8x + 1)
= ½ (1/2 (x2 – 8x + 1)2) + c
= ½ (x2 – 8x + 1)2 + c

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Math, University of Tennessee, Math is Fun, Siyavula

Rumus Kalkulus – Limit, Turunan, Integral, Teorema Dasar, Contoh Soal dan Jawaban

Kalkulus

Prinsip-prinsip dasar Kalkulus dan Rumus Kalkulus