Panjang Gelombang

Panjang gelombang adalah sebuah jarak antara satuan berulang dari sebuah pola gelombang. Biasanya memiliki denotasi huruf Yunani lambda (λ).

Gelombang sinus

Dalam sebuah gelombang sinus, panjang gelombang adalah jarak antara puncak:

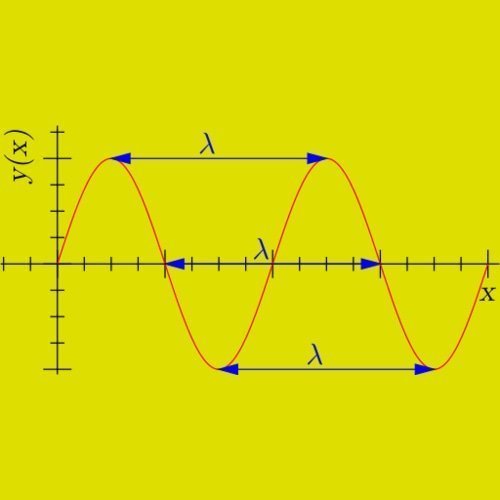
Axis x mewakilkan panjang, dan I mewakilkan kuantitas yang bervariasi (misalnya tekanan udara untuk sebuah gelombang suara atau kekuatan listrik atau medan magnet untuk cahaya), pada suatu titik dalam fungsi waktu x.

Panjang gelombang λ memiliki hubungan inverse terhadap frekuensi f, jumlah puncak untuk melewati sebuah titik dalam sebuah waktu yang diberikan.

Panjang gelombang sama dengan kecepatan jenis gelombang dibagi oleh frekuensi gelombang.

Ketika berhadapan dengan radiasi elektromagnetik dalam ruang hampa, kecepatan ini adalah kecepatan cahaya c, untuk sinyal (gelombang) di udara, ini merupakan kecepatan suara di udara. Hubungannya adalah:

λ = c / f

di mana:

λ = panjang gelombang dari sebuah gelombang suara atau gelombang elektromagnetik

c = kecepatan cahaya dalam ruang hampa = 299.792.458 m/s ~ 300.000 km/s = 300.000.000 m/s atau

c = kecepatan suara dalam udara = 344 m/s pada 20 °C (68 °F)

f = frekuensi gelombang

Gelombang tegak

Sebuah gelombang tegak adalah gerakan tidak terikat yang tetap di satu tempat. Gelombang tegak sinusoidal mencakup titik-titik diam tanpa gerakan, disebut node, dan panjang gelombang dua kali jarak antara node.

Panjang gelombang angular

Kuantitas yang terkait dengan panjang gelombang adalah panjang gelombang angular (juga dikenal sebagai panjang gelombang yang dikurangi), biasanya dilambangkan dengan ƛ (lambda-bar).

Hal ini sama dengan “panjang gelombang” biasa “yang dikurangi” dengan faktor 2π (ƛ = λ / 2π). Ini biasanya ditemui dalam mekanika kuantum, di mana ia digunakan dalam kombinasi dengan konstanta Planck yang berkurang (simbol ħ, h-bar) dan frekuensi angular (simbol ω) atau bilangan gelombang angular (simbol k).

Sub panjang gelombang

Istilah Sub panjang gelombang dapat digunakan untuk menggambarkan objek yang memiliki satu atau lebih dimensi lebih kecil dari panjang gelombang yang digunakan untuk berinteraksi.

Sebagai contoh, istilah serat optik berdiameter bawah gelombang berarti serat optik yang diameternya kurang dari panjang gelombang cahaya yang merambat melaluinya.

Partikel Sub panjang gelombang adalah partikel yang lebih kecil dari panjang gelombang cahaya yang berinteraksi dengannya (hamburan Rayleigh).

Lubang sub panjang gelombang adalah lubang yang lebih kecil dari panjang gelombang cahaya yang merambat melaluinya.

Struktur semacam itu memiliki aplikasi dalam transmisi optik yang luar biasa, dan pemandu gelombang mode-nol, di antara bidang fotonik lainnya.

Sub panjang gelombang juga bisa merujuk pada fenomena yang melibatkan objek subwavelength; misalnya, pencitraan sub panjang gelombang.

---

---

Contoh Soanl dan Jawaban Panjang Gelombang

1. Periode suatu gelombang adalah 0,02 s dengan panjang gelombang sebesar 25 meter. Hitunglah cepat rambat gelombangnya! 

Periode T = 0,02 s
Panjang gelombang λ = 25 m

Ditanya: Cepat rambat ν =………?

ν = λ / T ν = 25 / 0,02 ν = 1250 m/s

6. Suatu sumber bunyi bergerak menjauhi seorang Pendengar yang tidak bergerak dengan kecepatan 108 km/jam. Apabila frekuensinya 120 Hz dan Cepat rambat bunyi di udara 340 m/s, tentukanlah frekuensi yang terdengar oleh Pendengar !

Penyelesaian
Diketahui:
VP    =  0
VS    =  108 km/jam  =  108.000/3600  =  30 m/s
fS    =  120 Hz
V    =  340 m/s
Ditanya    :  fP
Jawab
fP    =  (V ± V_P)/(V ±V_s ) .fS
=  (V+ V_P)/(V+ V_S ) . fS
=  (340+0)/(340+30) . 120
=  110,27 Hz

7. Sebuah tali membentuk gelombang dengan amplitude 20cm dan frekuensi 20 Hz. Di asumsikan bahwa tali elastic sempurna dan bagian-bagian tali yang bergetar memiliki massa 2 gram. Tentukan energy kinetic dan energy potensial setelah gelombang merambat selama 2 sekon.

Penyelesaian:
Diketahui:

A = 20 cm = 0,2 m
m = 2 g = 0,002 kg
f = 20 Hz
t = 2 s

ditanyakan :
Ep dan Ek pada saat t = 2s adalah…..?

Jawab:

Ep = ½ ky² = ½ k A² sin² ωt = ½ m ω² A² sin² ωt
= ½ (0,002). (2. 3,14.20)² . (0,2)² (sin(π. 20.2))²
= ½ (0,002) . (2. 3,14.20)² . (0,02)² . 1
= 0,621 J

8. Sebuah gelombang pada permukaan air dihasilkan dari suatu getaran yang frekuensinya 30 Hz. Jika jarak antara puncak dan lembah gelombang yang berturutan adalah 50 cm, hitunglah cepat rambat gelombang tersebut!

Penyelesaian:
Diketahui : f = 30 Hz , ½ λ = 50 cm à λ = 100 cm = 1 m
Ditanya : v = ..?

Jawaban:
v = λ.f = 1.30 = 30 m/s

9. Sebuah pemancar radio bekerja pada gelombang 1,5 m. Jika cepat rambat gelombang radio 3.108 m/s, pada frekuensi berapakah stasion radio tersebut bekerja!

Penyelesaian:
Diketahui : λ = 1,5 m, v = 3.108 m/s
Ditanya : f = ..?

Jawaban:
f = 2. 108 Hz = 200 MHz

10. Seutas tali tampar yang panjangnya 250 m direntangkan horizontal. Salah satu ujungnya digetarkan dengan frekuensi 2 Hz dan amplitude 10 cm, sedang ujung lainnya terikat . Getaran tersebut merambat pada tali dengan kecepatan 40 cm/s. tentukan :

(a) Amplitudo gelombang stasioner di titik yang berjarak 132,5 cm dari titik asal getaran
(b) Simpangan gelombang pada titik tersebut setelah digetarkan selama 5 s dan 12 s
(c) Letak simpul keenam dan perut kelima dari titik asal getaran

Jawaban:

(a) titik asal getaran yaitu = 250 – 132,5 = 117,5 cm ,
Aѕ = 2A sin (2π x/λ) = 2.10 sin (360. 117,5/20) = 20 sin 315 = -10√2
Nilai ampitudo diambil nilai positifnya yaitu 10√2

(b) t = 250 + 117,5/40 = 9,2 sekon
ys = 2A sin kx cos ωt
ys = As cos ωt = (-10√2) cos 2π. 12/0,5 = (-10√2.cos 48π) = 10√2cm

(c ) simpul keenam = 50 cm dai ujung pantul
Perut kelima = 45 cm dari ujung pantul

11. Dalam 2 menit terjadi 960 getaran pada suatu partikel. Tentukan:
a) periode getaran
b) frekuensi getaran

Penyelesaian/
Diket :
Jumlah getaran n = 960
waktu getar t = dua menit = 120 sekon

a) periode getaran
T = t /n
T = 120 / 960 sekon
T = 0,125 sekon

b) frekuensi getaran
f = n/t
f = 960 / 120
f = 8 Hz

12. Frekuensi suatu getaran adalah 5 Hz. Tentukan:
a) periode getaran
b) banyak getaran yang terjadi dalam 2 menit

Penyelesaian:
Diketahui:
a) T = 1/f
T = 1/5
T = 0,2 sekon

b) n = t x f
n = 120 x 5
n = 600 getaran

13. Sebuah gelombang merambat dengan kecepatan 340 m/s. Jika frekuensi gelombang adalah 50 Hz, tentukan panjang gelombangnya!

Penyelesaian:
Diketahui:
ν = 340 m/s
f = 50 Hz
λ = ………..

λ = ν / f
λ = 340 / 50
λ = 6,8 meter

14. Periode suatu gelombang adalah 0,02 s dengan panjang gelombang sebesar 25 meter. Hitunglah cepat rambat gelombangnya!

Penyelesaian:
Diketahui:

Periode T = 0,02 s
Panjang gelombang λ = 25 m
Cepat rambat ν =………

λ = T ν
ν = λ / T
ν = 25 / 0,02
ν = 1250 m/s

15. Duah buah Garputala bergetar secara bersama-sama dengan frekuensi masing-masing 416 Hz dan 418 Hz

Penyelesaian:
Diketahui:
f1    =  416 Hz
f2    =  418 Hz
Ditanya:
fl
Tl
Jawab
fl   =  f2 –f1
=  418 – 416
=  2 Hz
Tl   =  1/fl
=  1/2 detik

16. Periode suatu getaran adalah 1/2 detik. Tentukan:
a) frekuensi getaran
b) jumlah getaran dalam 5 menit

Penyelesaian:
Diket :
T = 1/2 sekon
t = 5 menit = 5 x 60 = 300 sekon
a) frekuensi getaran
f = 1/T
f = 1/(0,5)
f = 2 Hz

b) jumlah getaran dalam 5 menit = 300 sekon
n = t x f
n = 300 x 4
n = 1200 getaran

17. Sebuah mesin jahit yang sedang bekerja mempunyai intensitas bunyi 10-8 W/m2. Apabila intensitas ambang bunyi 10-12 wb/m2, hitunglah Taraf intensitas bunyi dari 10 mesin jahit sejenis yang sedang bekerja bersama-sama !

Penyelesaian:
Diketahui:
I1    =  10-8 Watt/m2
Io    =  10-12 Watt/m2
Ditanya    :  TI10
Jawab        :
TI10    =   10 log I_10/Io             I10   = 10.I1  =  10.10-8  =  10-7 Watt/m2
=  10 log 〖10〗^(-7)/〖 10〗^(-12)
=  10 (log 10-7 – log 10-12)
=  10 (-7 + 12)
=  10. 5
=  50 dB

18. Pemancar Radio yang berfrekuensi 10.000 Hz mempunyai Panjang gelombang 150 cm. tentukan Cepat rambat bunyi tersebut!

Penyelesaian:
Diketahui:
f    =  10.000 Hz
λ    =  150 cm  = 1,5 m
Ditanya    :  V
Jawab
V    =  λ. f
=  1,5. 10.000
=  15.000 m/s