Teorema Rolle dalam Kalkulus
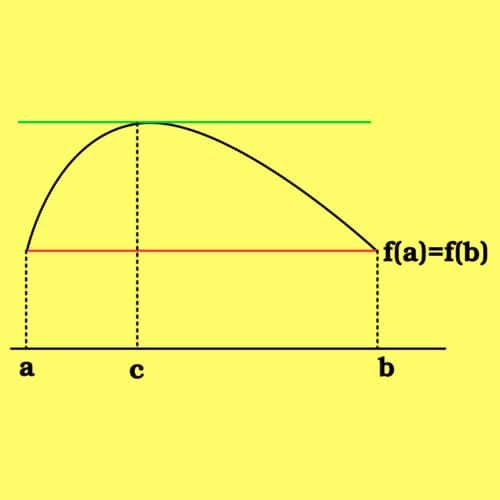
Dalam kalkulus, Teorema Rolle pada dasarnya menyatakan fungsi diferensiabel dan kontinu, yang memiliki nilai sama pada dua titik, mestilah memiliki titik stasioner yang terletak di antara kedua titik tersebut. Pada titik stasioner ini, gradien garis singgung terhadap fungsi tersebut sama dengan nol.
Versi standar Teorema Rolle
Bila sebuah fungsi riil f kontinu pada selang tertutup [a, b], terdiferensialkan pada selang terbuka (a, b), dan ƒ(a) = ƒ(b), maka ada bilangan c dalam selang terbuka (a, b) sedemikian sehingga
Versi Teorema Rolle ini digunakan untuk membuktikan teorema nilai purata atau teorema nila rata-rata, yang merupakan kasus umum daripada teorema Rolle.
Generalisasi Teorema Rolle
Contoh berikut mengilustrasikan generalisasi daripada teorema Rolle:
Perhatikan fungsi riil, kontinu dalam selang tertutup [a, b] dengan f(a) = f(b). Bila untuk setiap x dalam selang terbuka (a,b) limit kanan
dan limit kiri
ada pada garis bilangan riil yang diperluas [−∞,∞], maka ada suatu bilangan c pada selang terbuka (a,b) sehingga salah satu dari dua limit
adalah ≥ 0 dan yang lainnya adalah ≤ 0 (pada garis bilangan riil yang diperluas). Bila limit kiri dan kanan sama untuk setiap x, maka limit ini sama pada khususnya untuk c. Jadi turunan f ada pada c dan sama dengan nol.
Komentar
- Bila f adalah cekung atau cembung, maka turunan kiri atau kanan ada pada setiap titik dalam, sehingga kedua limit di atas ada dan merupakan bilangan riil
- Versi yang digeneralisasi ini cukup untuk membuktikan kecekungan fungsi bila salah satu turunan searah naik monoton:
Pembuktian Teorema Rolle
Di sini akan dibuktikan teorema yang sudah digeneralisasi.
Gagasan dasarnya adalah bahwa bila f(a) = f(b), maka f mestilah mencapai maksimum atau minimum di suatu titik antara a dan b. Sebutlah titik ini c. Fungsi tersebut juga harus berubah dari naik menjadi turun (atau sebaliknya) pada c. Khususnya, bila turunannya ada, nilainya mestilah nol pada c.
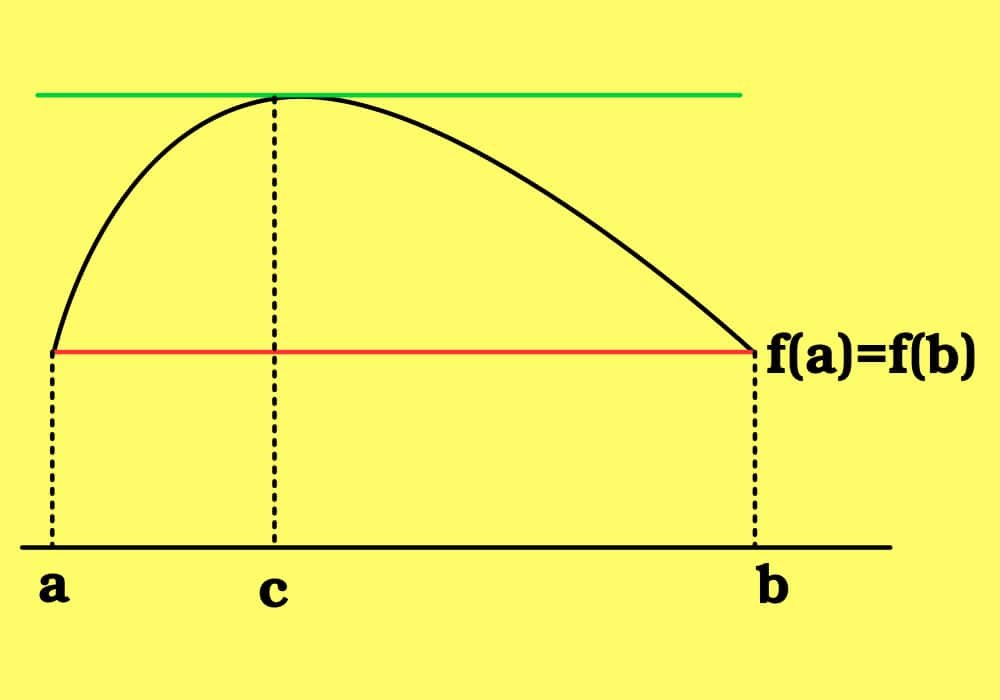
Dari asumsi, diketahui f kontinu pada [a,b] dan menurut teorema nilai ekstrem mencapai baik maksimum maupun minimumnya dalam [a,b]. Bila keduanya dicapai pada titik batas [a,b] maka fadalah fungsi konstan pada [a,b] dan turunannya adalah nol pada setiap titik pada (a,b).
Misalkan bila maksimum diperoleh pada titik dalam c pada selang (a, b) (argumen untuk nilai minimum mirip, perhatikan −f ). Kita akan memeriksa limit kanan dan kiri secara terpisah.
Untuk h riil sedemikian sehingga c + h adalah dalam [a,b], nilai f(c + h) lebih kecil atau sama dengan f(c) karena f mencapai maksimumnya pada c. Karena itu, untuk setiap h > 0,
sehingga
di mana limit ada menurut asumsi, yang bisa saja bernilai minus tak terhingga
Dengan cara yang sama, untuk setiap h < 0, tanda pertidaksamaan berbalik karena penyebutnya negatif dan kita mendapatkan
jadi
sehingga limitnya bisa saja plus tak terhingga
Akhirnya, ketika limit kanan dan kiri di atas sama, (terutama bila f terdiferensialkan), maka turunan f di c haruslah nol.
Teorema nilai ekstrem, digunakan untuk membuktikan Teorema Rolle
Contoh Soal dan Jawaban Teorema Rolle
Tunjukkan bahwa hipotesa teorema rolle terpenuhi pada selang yang diberikan dan tentukan semua nilai c yang memenuhi.
f(x) = x³ – 3x² + 2x; [0,2]
Jawaban:
f(x) = x³ – 3x² + 2x
f(0) = 0
f(2) = 2³ – 3 2² + 2 2 = 0
f(0) = f(2) = 0
f'(c) = 0
3c^2 – 6c + 2 = 0
dg rumus abc didapat
c = 1 ± 1/3 √3
Tunjukkan bahwa hipotesa teorema rolle terpenuhi pada selang yang diberikan dan tentukan semua nilai c yang memenuhi.
f(x) = (x² – 1)/(x² – 2); [-1, 1]
Jawaban:
f(x) = (x² – 1)/(x² – 2)
f(-1) = f(1) = 0
f'(c) = 0
-2c / (x^4 – 4x^2 + 4) = 0
c = 0
Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar
- Fungsi Matematika: Linear, Konstan, Identitas – Beserta Soal dan Jawaban
- Topologi Matematika – Contoh Soal dan Jawaban Ruang Topologi
- Rumus Matematika Keuangan – Contoh Soal dan Jawaban
- Induksi Matematika Rumus, Pembuktian, Deret, Keterbagian, Pertidaksamaan, Soal, Pembahasan dan Jawaban
- Jenis dan Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
- Berapa Kecerdasan IQ Anda? Tes IQ Anda Disini
- Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
- 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
- Tulisan Menunjukkan Kepribadian Anda & Bagaimana Cara Anda Menulis?
- Penyakit yang dapat dicegah dengan vaksin – Wajib diketahui
- Top 10 Sungai Terpanjang Di Dunia
- Tempat Wisata Yang Wajib Dikunjungi Di Indonesia Dan Luar Negri
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
- Bentuk Kaki Menandakan Karakter Anda – Bentuk Kaki nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing









![{\displaystyle f(c)\geq f(x)\geq f(d)\quad {\text{untuk semua }}x\in [a,b].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e95777a694ab6c7394818c0a4c7f31c1e6aa85c)