Rumus, Penjelasan dan Bunyi Hukum Kepler

Berikut bunyi Hukum Kepler 1, 2, 3:

1. Rumus Hukum Kepler 1

Hukum Kepler 1: Lintasan orbit setiap planet ketika mengelilingi matahari berbentuk elips dimana matahari terletak pada salah satu fokusnya.

Merupakan suatu efek langsung akibat sifat kuadrat terbalik dari gaya gravitasi bumi. Seperti yang kita tahu bahwa matahari dan benda-benda asing luar angkasa lainnya memiliki variasi sebagai jalur untuk mencakup objek parabola (e = 1) dan hiperbola (e > 1) , jarak pemisahan dan kuadrat balik.

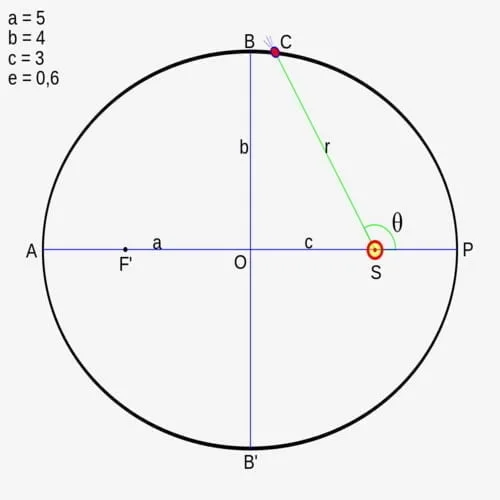
Ini ada ilustrasi dari gambaran elips, yang mana:

a : sumbu Panjang
b : sumbu pendek
ae : perbandingan jarak antara titik fokus I dan II.
r₀: Semi-latus rectum, jari-jari yang sejajar dengan sumbu pendek dari titik fokus II.
r : Jarak antara matahari dan planet
M : Matahari, dimana massa (M>m)
m : Planet

Perlu diketahui bahwa semakin dekat fokus-fokus elipnya, maka bentuknya hampir mendekati lingkaran. Perbandingan dari sebuah lingkaran adalah nol, oleh sebab itu maka syarat nilai elips ialah e>0.

Di dalam lintasan planet berbentuk elips, secara sistematis dirumuskan menjadi:

2. Rumus Hukum Kleper 2

Hukum Kepler 2: Garis khayal yang menghubungkan planet dengan matahari mencakup luas daerah yang sama dalam interval waktu yang sama.

Jika sebuah planet membutuhkan waktu yang sama untuk menempuh P1 – P2 dan P3 – P4, maka luas dari areal P1 – F – P2 akan sebanding dengan F – P4. Hal ini bisa dikatakan bahwa kecepatan dari angulernya konstan.

{\frac {d}{dt}}({\frac {1}{2}}r^{2}{\dot {\theta }})=0

dimana ${\frac {1}{2}}r^{2}{\dot {\theta }}$ adalah “areal velocity”.

3. Rumus Hukum Kleper 3

Hukum Kepler 3: Kuadrat periode orbit suatu planet sebanding dengan pangkat tiga jarak rata-ratanya dari matahari.

Merupakan sebuah hukum yang diprediksikan tentang hukun kuadrat terblik pada orbit lingkaran. Untuk rumus sistematis di Hukum Kleper 3 dapat diasumsikan sebagai M_p(Massa Planet) dan M_s(matahari yang sedang mengorbit).

Adanya suatu gaya gravitasi pada sebuah lingkaran, maka hal itu memberikan sebuah sentripetal planet saat bergerak. Secara sistematis, dapat di perhitungkan sebagai berikut:

F_g= M_pa → = M_p (v²/r)

Sedangkan untuk perhitungan kecepatan orbitan planet ialah 2pr / T, dan di mana K_s adalah konstanta yang diberikan pada:

K_s= =2,97 x 10^-19 s²/m³

Hukum Kepler

Berikut adalah pengenalan 3 hukum Kepler.

Secara umum, Hukum hukum ini menjabarkan gerakan dua badan yang mengorbit satu sama lainnya. Massa dari kedua badan ini bisa hampir sama, sebagai contoh Charon—Pluto (~1:10), proporsi yang kecil, sebagai contoh. Bulan—Bumi(~1:100), atau perbandingan proporsi yang besar, sebagai contoh Merkurius—Matahari (~1:10,000,000).

Dalam semua contoh di atas, kedua badan mengorbit mengelilingi satu pusat massa, barycenter, tidak satu pun berdiri secara sepenuhnya di atas fokus elips. Namun, kedua orbit itu adalah elips dengan satu titik fokus di barycenter. Jika rasio massanya besar, sebagai contoh planet mengelilingi Matahari, barycenternya terletak jauh di tengah objek yang besar, dekat di titik massanya. Di dalam contoh ini, perlu digunakan instrumen presisi canggih untuk mendeteksi pemisahan barycenter dari titik masa benda yang lebih besar. Jadi, hukum Kepler pertama secara akurat menjabarkan orbit sebuah planet mengelilingi Matahari.

Karena Kepler menulis hukumnya untuk aplikasi orbit planet dan Matahari, dan tidak mengenal generalitas hukumnya, artikel ini hanya akan mendiskusikan hukum di atas sehubungan dengan Matahari dan planet-planetnya.

1. Penjelasan Hukum Kepler Pertama

“Setiap planet bergerak dengan lintasan elips, Matahari berada di salah satu fokusnya.”

Hukum ini menjelaskan periode revolusi planet-planet yang mengelilingi matahari. Planet memiliki periode orbit yang lebih panjang ketika planet tersebut letaknya jauh dari matahari dan planet memiliki periode orbit yang lebih pendek ketika planet tersebut letaknya dekat dari matahari.

Pada zaman Kepler, klaim di atas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.

Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproksimasi lingkaran. Jadi, kalau ditilik dari pengamatan jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips.

Namun, dari bukti perhitungan Kepler, orbit-orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari Matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh, Pluto, yang diamati pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elips dan kecil ukurannya.

Hukum Kepler pertama menempatkan Matahari di satu titik fokus edaran elips. Sumber foto: Wikimedia Commons

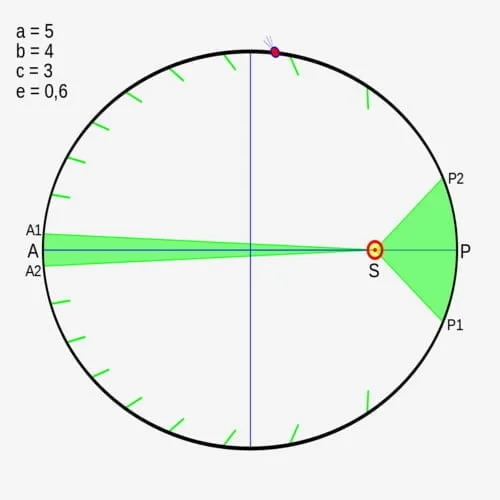
2. Penjelasan Hukum Kepler Kedua

“Luas daerah yang disapu pada selang waktu yang sama akan selalu sama.”

Hukum ini menjelaskan bahwa kecepatan orbit pada suatu planet akan lebih lambat ketika planet berada pada titik terjauh dari matahari (titik aphelion) dan kecepatan orbit suatu planet akan lebih cepat ketika planet berada pada titik terdekat dengan matahari (titik perihelion). Jadi, kecepatan orbit maksimum planet ketika berada di titik perihelion dan kecepatan orbit minimum planet ketika berada di titik aphelion.

Secara matematis rumus hukum kepler 2:

{\frac {d}{dt}}({\frac {1}{2}}r^{2}{\dot {\theta }})=0

dimana ${\frac {1}{2}}r^{2}{\dot {\theta }}$ adalah “areal velocity”.

Illustrasi hukum Kepler kedua. Bahwa Planet bergerak lebih cepat di dekat Matahari dan lambat di jarak yang jauh. Sehingga, jumlah area adalah sama pada jangka waktu tertentu. Sumber foto: Wikimedia Commons

3. Penjelasan Hukum Kepler Ketiga

Planet yang terletak jauh dari Matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepler ketiga menjabarkan hal tersebut secara kuantitatif.

“Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari Matahari.”

Secara matematis rumus hukum Kepler 2:

{P^{2}}\propto {a^{3}}

dengan $P$ adalah perioda orbit planet dan $a$ adalah sumbu semimajor orbitnya.

Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar Matahari.

{\frac {P_{\rm {planet}}^{2}}{a_{\rm {planet}}^{3}}}={\frac {P_{\rm {earth}}^{2}}{a_{\rm {earth}}^{3}}}.

Sejarah Hukum Kepler

Pada tahun 1601 Kepler berusaha mencocokkan berbagai bentuk kurva geometri pada data-data posisi Planet Mars yang dikumpulkan oleh Tycho Brahe.
Hingga tahun 1606, setelah hampir setahun menghabiskan waktunya hanya untuk mencari penyelesaian perbedaan sebesar 8 menit busur (mungkin bagi kebanyakan orang hal ini akan diabaikan), Kepler mendapatkan orbit planet Mars.
Menurut Kepler, lintasan berbentuk elips adalah gerakan yang paling sesuai untuk orbit planet yang mengitari matahari.
Pada tahun 1609, dia mempublikasikan Astronomia Nova yang menyatakan dua hukum gerak planet. Hukum ketiga tertulis dalam Harmonices Mundi yang dipublikasikan sepuluh tahun kemudian.

Hukum Gerakan Planet Kepler

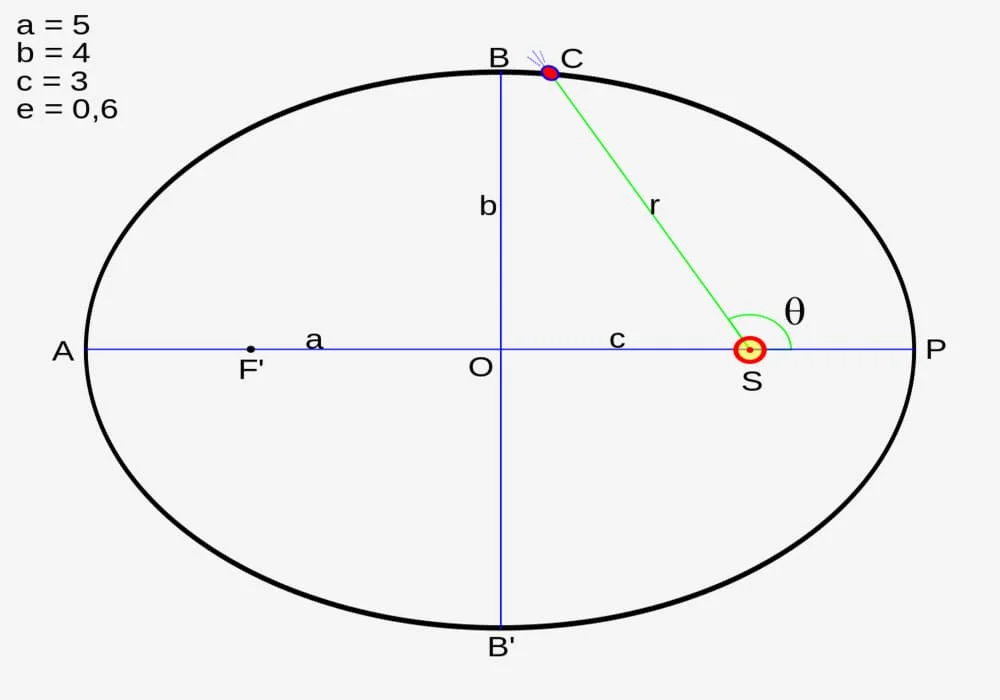
Figure 1: Illustration of Kepler’s three laws with two planetary orbits. (1) The orbits are ellipses, with focal points ƒ₁ and ƒ₂ for the first planet and ƒ₁ and &>. (2) The two shaded sectors A₁ and A₂ have the same surface area and the time for planet 1 to cover segment A₁ is equal to the time to cover segment A₂. (3) The total orbit times for planet 1 and planet 2 have a ratio a₁^3/2 : a₂^3/2.

Di dalam astronomi, 3 Hukum Gerakan Planet Kepler adalah:

Setiap planet bergerak dengan lintasan elips, Matahari berada di salah satu fokusnya.
Luas daerah yang disapu pada selang waktu yang sama akan selalu sama.
Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari Matahari.

Penemu hukum Kepler

Ketiga hukum di atas ditemukan oleh ahli matematika dan astronomi Jerman: Johannes Kepler (1571–1630), yang menjelaskan gerakan planet di dalam tata surya. Hukum di atas menjabarkan gerakan dua benda yang saling mengorbit.

Karya Kepler didasari oleh data pengamatan Tycho Brahe, yang diterbitkannya sebagai ‘Rudolphine tables’. Sekitar tahun 1605, Kepler menyimpulkan bahwa data posisi planet hasil pengamatan Brahe mengikuti rumusan matematika cukup sederhana yang tercantum di atas.

Hukum Kepler mempertanyakan kebenaran astronomi dan fisika warisan zaman Aristoteles dan Ptolemaeus. Ungkapan Kepler bahwa Bumi beredar sekeliling, berbentuk elips dan bukannya epicycle, dan membuktikan bahwa kecepatan gerak planet bervariasi, mengubah astronomi dan fisika. Hampir seabad kemudian, Isaac Newton mendeduksi Hukum Kepler dari rumusan hukum karyanya, hukum gerak dan hukum gravitasi Newton, dengan menggunakan Euclidean geometri klasik.

Penggunaan hukum Kepler

Pada era modern, hukum Kepler digunakan untuk aproksimasi orbit satelit dan benda-benda yang mengorbit Matahari, yang semuanya belum ditemukan pada saat Kepler hidup (contoh: planet luar dan asteroid).

Hukum ini kemudian diaplikasikan untuk semua benda kecil yang mengorbit benda lain yang jauh lebih besar, walaupun beberapa aspek seperti gesekan atmosfer (contoh: gerakan di orbit rendah), atau relativitas (contoh: prosesi preihelion merkurius), dan keberadaan benda lainnya dapat membuat hasil hitungan tidak akurat dalam berbagai keperluan.

Animasi dari gerak Kepler

Fungsi Hukum Kepler

Untuk di zaman yang modern ini, Hukum Kepler sudah resmi digunakan untuk mengamati sebuah orbitan dari matahari. Dari sinilah para ilmuwan memperkirakan lintasan dari planet luar dan asteroid yang mengorbit matahari.

Selain untuk mengamati tentang pengorbitan matahari, Hukum Kepler ini pun digunakan sebagai hukum untuk memperkirakan orbitan bumi dan bulan. Alat yang biasa digunakan untuk memperkirakan orbitan tersebut adalah asteroid, yang ukurannya mencapai 490 kaki atau 150 meteran.

Asteroid pengamat ini diberi nama dengan sebutan Asteroid 2014 OL339. Asteroid ini letaknya sangat dekat dengan bumi. Hanya dengan waktu 364,25 hari Asteroid dapat mengitari Matahari.

Demikianlah fungsi dari Hukum Kepler, berikutnya saya akan menjelaskan tentang pengertian dari bunyi dari Hukum Kepler.

Contoh Soal dan Jawaban Kepler

1. Jika ada planet A dan B sedang mengorbit matahari. Maka perbandingan antara jarak planet A dan B ke matahari (R_A : R_B = 1 : 4). Namun, jika periode planet A mengelilingi matahari ialah 88 hari maka periode planet B menjadi berapa hari?

Pembahasan

Diketahui:

R_A: R_B= 1 : 4
T_A= 88 hari.

Jadi periode T_Badalah:

(Tb/Ta)^2 = (Rb/Ra)^3
(Tb/88)^2 = (4/1)^3
(Tb/88)^2 = 4 x 4 x 4
Tb/88 = √(4 x 4 x 4)
Tb/88 = 2 x 2 x 2
Tb/88 = 8
Tb = 88 x 8
Tb = 704 hari

Jadi periode planet B atau T_B ialah 704 hari.

2. Waktu yang dibutuhkan Pluto untuk berputar mengelilingi matahari adalah selama 2 tahun, dengan jarak tempuh sebesar 1,5 x 10¹¹Apabila waktu yang dibutuhkan planet Saturnus untuk berputar mengelilingi matahari adalah selama 1 tahun, berapakah jarak antara planet Saturnus dengan Matahari?

Diketahui:

T_p = 2 tahun
r_p = 1,5 x 10¹¹ m
T_S = 2 tahun

Ditanyakan:

r_S?

Jawab:

(T_p)²/(r_p)³ = (T_S)²/(r_S)³

(1,5)²/(1,5 x 10¹¹)³ = (2)²/(r_S)³

(r_S)³ = (1,5 x 10¹¹)³ (2²/1,5²)

(r₂) = ∛6,008 x 10³³

Jadi, jarak antara planet Mars dengan matahari adalah sebesar ∛6,008 x 10³³ m.

3. Asumsikan jarak bulan ke Bumi adalah $3, 84 \times 10^{8}$ meter dan periode bulan mengelilingi Bumi adalah $2, 5 \times 10^{6}$ s. Hitung massa Bumi!

Penyelesaian dan jawaban:

Berdasarkan persamaan (5) maka

$\begin{aligned} M & = \frac{4 π^{2} R^{3}}{G T^{2}} \\ = \frac{4 π^{2} \times (3, 84 \times 10^{8})^{3}}{6, 674 \times 10^{- 11} \times {(2, 5 \times 10^{6})}^{2}} \\ = 5, 36 \times 10^{24} kg \end{aligned}$

4. Planet C dan D berputar mengelilingi matahari. Jika kedua planet memiliki jarak tempuh masing-masing 4:1, maka berapa perbandingan periode kedua planet tersebut?

Diketahui:

r_C : r_D = 4:1

Ditanyakan:

T_C : T_D?

Jawab:

Untuk menyelesaikan soal ini, kita gunakan rumus (k) dari hukum Kepler III:

k = T²/r³

k = T_C²/r_C³ = T_D²/r_D³

k = (T_C/T_D)² = (r_C/r_D)³

(T_C/T_D)² = (4/1)³

T_C/T_D = √4³ = 3√4

Jadi, perbandingan periode planet C dan D adalah sebesar 3√4.

5. Bumi membutuhkan waktu untuk mengelilingi Matahari selama 1 tahun, sedangkan jarak rata-rata antara Bumi dengan pusat tata surya yaitu sekitar 1,5 x 1011 m. Jika setelah diketahui bahwa periode orbit dari planet Venus ialah 0,615 tahun, maka berapakah jarak sebenarnya antara matahari dengan venus?

Pembahasan:

Jadi diketahui:

periode bumi : Tb = 1 Tahun
Jarak matahari ke bumi (Rm-b) = 1,5 x 1011 m
Periode venus = Tv = 0,615 tahun

Jadi berapakah Rm-v?

Dengan menggunakan Hukum Kepler 3 di atas, maka Anda bisa mengetahuinya bahwa jarak antara planet venus dan matahari ialah 1,084 x 1011 m. Planet ini diperkirakan lebih dekat jaraknya dengan matahari, jika dibandingkan dengan bumi.

6. Apabila jarak rata-rata bumi ke matahari ialah 149,6 x 10⁶ km dan periode revolusi pada bumi ialah 1 tahun. Maka berapakah konstanta perbandingan kuadrat periode pada pangkat tiga jarak antara matahari dan bumi?

Pembahasan:

Diketahui:

T = 1 tahun
r = 149,6 x 10⁶ km

Maka T²/r³ adalah….?

k = T² / r³= 1² / (149,6 x 10⁶)³ = 1 / (3348071,9 x 10¹⁸) = 2,98 x 10^-25tahun²/km^3.

Konstanta perbandingan pada suatu periode revolusi planet terhadap pangkat tiga jarak umum planet ke matahari sebanding dengan semua planet. Konstanta perbandingan ini dapat dihitung dengan melalui rumus:

k = 4π² / Gm

Keterangan:

Jika (G) atau konstanta gravitasi universal ialah 6,67 x 10^-11 N.m²/kg^{2 .}
Sedangkan (m) massa matahari yaitu 1,99 x 10³⁰ kg pi ialah 3,14.

Untuk menghitungnya, Anda perlu menggunakan rumus yang telah tertulis di atas. Untuk hitungan satuannya, gunakan periode = tahan dan satuan jarak = kilometer.

Pembahasan dan jawaban:

k = 4 (3,14)² / (6,67 x 10 ^–¹¹) x (1,99 x 10³⁰)

k = 39,4383 / 13,2733 x 10¹⁹

k = 2,97 x 10^-19s^2/m³

1 s^2/m³ = 1/31.538.000²: 1/1000³

1 s^2/m³= 1 x 10^-6tahun²/km³

k = (2,97 x 10^-19) (1 x 10^-6tahun²/km³)

k = 2,97 x 10^-25tahun²/km³

7. Jarak standar planet bumi ke matahari adalah 149,6 x 10⁶ km dan jarak standar planet merkurius 57,9 x 10⁶ Periode revolusi bumi adalah 1 tahun, jadi berapa periode revolusi pada planet merkurius ?

Pembahasan

Diketahui :

r bumi ialah 149,6 x 10⁶ km
r merkurius ialah 57,9 x 10⁶ km
T bumi ialah 1 tahun

Lalu, berapakah jarak merkuriusnya?

T₁² / r₁³= T₂²/ r₂³

1 = bumi, 2 = merkurius

1²/ (149,6 x 10⁶)³= T₂² / (57,9 x 10⁶)³

1 / 3348071,936 x 10¹⁸= T₂²/ 194104,539 x 10¹⁸

194104,539 x 10¹⁸/ 3348071,936 x 10¹⁸= T₂²

T₂²= 0,057975

T₂= √0,057975

Jadi T2 ialah 0,24 tahun bumi

1 tahun bumi ialah 365 hari, dan periode revolusi merkurius ialah (0.24)(365) = 87,6 hari.

8. Planet A dan B sama-sama berputar mengelilingi matahari. Perbandingan jarak planet A dan B adalah 1:6. Jika planet A mengelilingi matahari selama 90 hari, maka berapa waktu tempuh dari planet B?

Diketahui:

r_a : r_b = 1:6
T_A = 90 hari

Ditanyakan:

T_B?

Jawab:

k = T²/r³

k = T_A²/r_A³ = T_B²/r_B³

k = (90)²/(1)³ = T_B²/(6)³

T_B = √(6)³ x (90)²

T_B = 36 x 90 = 3240 hari

Jadi, planet B mengelilingi matahari selama 3240 hari.

9. Untuk mengelilingi matahari, bumi membutuhkan waktu tempuh selama 1 tahun. Jarak tempuh antara matahari dan bumi adalah sebesar 1, 6 x 10¹¹ Jika periode orbit dari planet Mars adalah 0,5 tahun, berapakah jarak antara planet Mars dengan matahari?

Diketahui:

Waktu tempuh atau periode bumi (Tb) = 1 tahun

r₁ = 1,6 x 10¹¹ m

waktu tempuh Mars (Tm) = 0,5 tahun

Ditanyakan:

r₂?

Jawab:

(Tb)²/(r₁)³ = (Tm)²/(r₂)³

(1)²/(1,6 x 1,0¹¹)³ = (0,5)²/(r₂)³

(r₂)³ = (1,6 x 10¹¹)³ (0,5²/1²)

(r₂) = ∛1,24 x 10³³

Jadi, jarak antara planet Mars dengan matahari adalah sebesar ∛1,24 x 10³³ m.

Bacaan Lainnya

Kilometer ke Tahun Cahaya - 1 Tahun Cahaya = 9,460,730,472,580.8 km — Peta menunjukkan bintang-bintang yang terletak dalam 12,5 tahun cahaya dari Matahari. Sumber foto: Wikimedia Commons

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Physics Classroom, Hyperphysics, NASA, Earth

Hukum Kepler Pertama, Kedua dan Ketiga Hukum – Rumus, Bunyi Hukum, Soal dan Jawaban

Rumus, Penjelasan dan Bunyi Hukum Kepler

1. Rumus Hukum Kepler 1

2. Rumus Hukum Kleper 2

3. Rumus Hukum Kleper 3

Hukum Kepler

1. Penjelasan Hukum Kepler Pertama

2. Penjelasan Hukum Kepler Kedua

Secara matematis rumus hukum kepler 2:

3. Penjelasan Hukum Kepler Ketiga

Secara matematis rumus hukum Kepler 2:

Sejarah Hukum Kepler

Hukum Gerakan Planet Kepler

Di dalam astronomi, 3 Hukum Gerakan Planet Kepler adalah:

Penemu hukum Kepler

Penggunaan hukum Kepler

Fungsi Hukum Kepler

Contoh Soal dan Jawaban Kepler

1. Jika ada planet A dan B sedang mengorbit matahari. Maka perbandingan antara jarak planet A dan B ke matahari (R_A : R_B = 1 : 4). Namun, jika periode planet A mengelilingi matahari ialah 88 hari maka periode planet B menjadi berapa hari?

2. Waktu yang dibutuhkan Pluto untuk berputar mengelilingi matahari adalah selama 2 tahun, dengan jarak tempuh sebesar 1,5 x 10¹¹Apabila waktu yang dibutuhkan planet Saturnus untuk berputar mengelilingi matahari adalah selama 1 tahun, berapakah jarak antara planet Saturnus dengan Matahari?

3. Asumsikan jarak bulan ke Bumi adalah $3, 84 \times 10^{8}$ meter dan periode bulan mengelilingi Bumi adalah $2, 5 \times 10^{6}$ s. Hitung massa Bumi!

4. Planet C dan D berputar mengelilingi matahari. Jika kedua planet memiliki jarak tempuh masing-masing 4:1, maka berapa perbandingan periode kedua planet tersebut?

6. Apabila jarak rata-rata bumi ke matahari ialah 149,6 x 10⁶ km dan periode revolusi pada bumi ialah 1 tahun. Maka berapakah konstanta perbandingan kuadrat periode pada pangkat tiga jarak antara matahari dan bumi?

7. Jarak standar planet bumi ke matahari adalah 149,6 x 10⁶ km dan jarak standar planet merkurius 57,9 x 10⁶ Periode revolusi bumi adalah 1 tahun, jadi berapa periode revolusi pada planet merkurius ?

8. Planet A dan B sama-sama berputar mengelilingi matahari. Perbandingan jarak planet A dan B adalah 1:6. Jika planet A mengelilingi matahari selama 90 hari, maka berapa waktu tempuh dari planet B?

9. Untuk mengelilingi matahari, bumi membutuhkan waktu tempuh selama 1 tahun. Jarak tempuh antara matahari dan bumi adalah sebesar 1, 6 x 10¹¹ Jika periode orbit dari planet Mars adalah 0,5 tahun, berapakah jarak antara planet Mars dengan matahari?

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

One Reply to “Hukum Kepler Pertama, Kedua dan Ketiga Hukum – Rumus,…”

Tinggalkan Balasan Batalkan balasan

Hukum Kepler Pertama, Kedua dan Ketiga Hukum – Rumus, Bunyi Hukum, Soal dan Jawaban

Rumus, Penjelasan dan Bunyi Hukum Kepler

1. Rumus Hukum Kepler 1

2. Rumus Hukum Kleper 2

3. Rumus Hukum Kleper 3

Hukum Kepler

1. Penjelasan Hukum Kepler Pertama

2. Penjelasan Hukum Kepler Kedua

Secara matematis rumus hukum kepler 2:

3. Penjelasan Hukum Kepler Ketiga

Secara matematis rumus hukum Kepler 2:

Sejarah Hukum Kepler

Hukum Gerakan Planet Kepler

Di dalam astronomi, 3 Hukum Gerakan Planet Kepler adalah:

Penemu hukum Kepler

Penggunaan hukum Kepler

Fungsi Hukum Kepler

Contoh Soal dan Jawaban Kepler

1. Jika ada planet A dan B sedang mengorbit matahari. Maka perbandingan antara jarak planet A dan B ke matahari (RA : RB = 1 : 4). Namun, jika periode planet A mengelilingi matahari ialah 88 hari maka periode planet B menjadi berapa hari?

2. Waktu yang dibutuhkan Pluto untuk berputar mengelilingi matahari adalah selama 2 tahun, dengan jarak tempuh sebesar 1,5 x 1011 Apabila waktu yang dibutuhkan planet Saturnus untuk berputar mengelilingi matahari adalah selama 1 tahun, berapakah jarak antara planet Saturnus dengan Matahari?

3. Asumsikan jarak bulan ke Bumi adalah 3,84×1083,84×108 meter dan periode bulan mengelilingi Bumi adalah 2,5×1062,5×106 s. Hitung massa Bumi!

4. Planet C dan D berputar mengelilingi matahari. Jika kedua planet memiliki jarak tempuh masing-masing 4:1, maka berapa perbandingan periode kedua planet tersebut?

6. Apabila jarak rata-rata bumi ke matahari ialah 149,6 x 106 km dan periode revolusi pada bumi ialah 1 tahun. Maka berapakah konstanta perbandingan kuadrat periode pada pangkat tiga jarak antara matahari dan bumi?

7. Jarak standar planet bumi ke matahari adalah 149,6 x 106 km dan jarak standar planet merkurius 57,9 x 106 Periode revolusi bumi adalah 1 tahun, jadi berapa periode revolusi pada planet merkurius ?

8. Planet A dan B sama-sama berputar mengelilingi matahari. Perbandingan jarak planet A dan B adalah 1:6. Jika planet A mengelilingi matahari selama 90 hari, maka berapa waktu tempuh dari planet B?

9. Untuk mengelilingi matahari, bumi membutuhkan waktu tempuh selama 1 tahun. Jarak tempuh antara matahari dan bumi adalah sebesar 1, 6 x 1011 Jika periode orbit dari planet Mars adalah 0,5 tahun, berapakah jarak antara planet Mars dengan matahari?

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

Tes matematika logika: Jika 4 + 3 = 27,…

Nilai Pi 1 juta digit pertama | Analisis dan…

One Reply to “Hukum Kepler Pertama, Kedua dan Ketiga Hukum – Rumus,…”

Tinggalkan Balasan Batalkan balasan

1. Jika ada planet A dan B sedang mengorbit matahari. Maka perbandingan antara jarak planet A dan B ke matahari (R_A : R_B = 1 : 4). Namun, jika periode planet A mengelilingi matahari ialah 88 hari maka periode planet B menjadi berapa hari?

2. Waktu yang dibutuhkan Pluto untuk berputar mengelilingi matahari adalah selama 2 tahun, dengan jarak tempuh sebesar 1,5 x 10¹¹Apabila waktu yang dibutuhkan planet Saturnus untuk berputar mengelilingi matahari adalah selama 1 tahun, berapakah jarak antara planet Saturnus dengan Matahari?

3. Asumsikan jarak bulan ke Bumi adalah $3, 84 \times 10^{8}$ meter dan periode bulan mengelilingi Bumi adalah $2, 5 \times 10^{6}$ s. Hitung massa Bumi!

6. Apabila jarak rata-rata bumi ke matahari ialah 149,6 x 10⁶ km dan periode revolusi pada bumi ialah 1 tahun. Maka berapakah konstanta perbandingan kuadrat periode pada pangkat tiga jarak antara matahari dan bumi?

7. Jarak standar planet bumi ke matahari adalah 149,6 x 10⁶ km dan jarak standar planet merkurius 57,9 x 10⁶ Periode revolusi bumi adalah 1 tahun, jadi berapa periode revolusi pada planet merkurius ?

9. Untuk mengelilingi matahari, bumi membutuhkan waktu tempuh selama 1 tahun. Jarak tempuh antara matahari dan bumi adalah sebesar 1, 6 x 10¹¹ Jika periode orbit dari planet Mars adalah 0,5 tahun, berapakah jarak antara planet Mars dengan matahari?