Penjelasan Median (Nilai Tengah)

Median adalah nilai tengah dari data yang telah disusun berurutan mulai dari yang terkecil sampai dengan yang terbesar. Secara matematis median dilambangkan dengan Me yang dapat dicari dengan cara sebagai berikut.

Bagaimana Cara Menghitung Median?

Untuk mencarinya, tempatkan semua angka dalam urutan naik dan temukan tengahnya.

Rumus Median

1. Median untuk jumlah data (n) ganjil

Me = x [(n+1) / 2]

atau

Median pada data yang ganjil = suku yang tepat berada di tengah

2. Median untuk jumlah data (n) genap

3. Median untuk data bergolong atau berkelompok

Me = Tb + [ (½ n-F) / f ] C

Keterangan:
Me = median
Tb = tepi bawah kelas median
p = panjang kelas
n = banyak data
F = frekuensi kumulatif sebelum kelas median
f = frekuensi kelas median

Contoh penghitungan Median

Untuk data ganjil

Untuk data 8, 7, 9. Pertama data diurutkan menjadi 7, 8, 9. Sehingga dengan mudah diketahui median adalah 8.

Untuk data genap

Untuk data 2, 8, 3, 4, 1, 8. Pertama data diurutkan menjadi 1, 2, 3, 4, 8, 8. Karena jumlah data pengamatan genap, yaitu 6, maka median terletak pada rata-rata dua nilai pengamatan yang di tengah yaitu data ketiga dan data keempat, maka mediannya adalah (3+4)/2 = 3,5.

Contoh:

3, 13, 7, 5, 21, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29

Ketika kita menyusun angka-angka itu, kita memiliki:

3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56

Ada 15 belas angka. Bagian tengah kita adalah angka kedelapan:

3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 39, 40, 56

Nilai median dari kumpulan angka ini adalah 23.

(Tidak masalah bahwa beberapa nomor sama dalam daftar.)

TAPI, dengan jumlah angka yang genap, hal-hal sedikit berbeda.

Dalam hal ini kita mencari pasangan angka tengah, dan kemudian mencari nilai setengah jalan di antara keduanya. Ini mudah dilakukan dengan menjumlahkan mereka dan membaginya dengan dua.

Contoh:
3, 13, 7, 5, 21, 23, 23, 40, 23, 14, 12, 56, 23, 29

Ketika kita menyusun angka-angka itu, kita memiliki:

3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 40, 56

Sekarang ada empat belas angka dan jadi kami tidak hanya memiliki satu angka tengah, kami memiliki sepasang angka tengah:

3, 5, 7, 12, 13, 14, 21, 23, 23, 23, 23, 29, 40, 56

Dalam contoh ini, angka tengahnya adalah 21 dan 23.

Untuk mencari nilai setengah di antara keduanya, jumlahkan keduanya dan bagi dengan 2:

21 + 23 = 44
kemudian 44 ÷ 2 = 22

Jadi Median dalam contoh ini adalah 22.

(Perhatikan bahwa 22 tidak ada dalam daftar angka … tetapi tidak apa-apa karena setengah angka dalam daftar lebih kecil, dan setengah angka lebih besar.)

Contoh 1:

Misal, median dari 3, 3, 5, 9, 11 adalah 5. Jika ada jumlah observasi nilai yang genap, maka tidak ada nilai tengah tunggal; median kemudian biasanya didefinisikan sebagai nilai tengah dari dua nilai tengah: jadi median dari 3, 5, 7, 9 adalah (5 + 7) / 2 = 6.

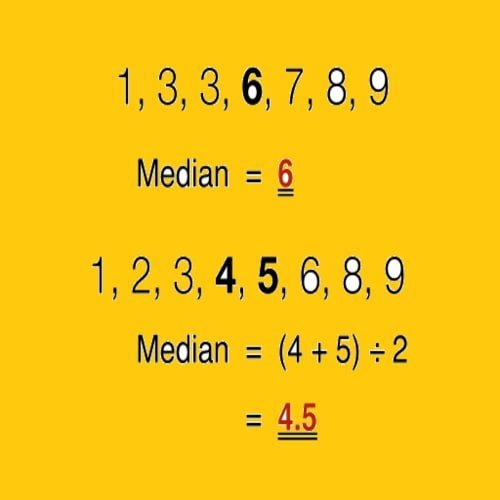
Contoh Soal dan Jawaban Median

Temukan median dari 14, 63 dan 55

Jawaban:

Urutkan dalam urutan naik: 14, 55, 63

Angka tengahnya adalah 55, jadi mediannya adalah 55.

Temukan median dari data berikut ini: 4, 17, 77, 25, 22, 23, 92, 82, 40, 24, 14, 12, 67, 23, 29

Jawaban:

Ketika kita memasukkan angka-angka itu dalam urutan yang kita miliki:

4, 12, 14, 17, 22, 23, 23, 24, 25, 29, 40, 67, 77, 82, 92,

Ada lima belas angka. Bagian tengah kita adalah angka kedelapan:

Nilai median dari kumpulan angka ini adalah 24.

Carilah nilai median dari data angka berikut ini  : 5,6,7,6,7,8,7,8,9 ?

Jawab :

Langkah awal yaitu kita urutkan datanya dari yang terkecil sampai yang terbesar.

data : 5,6,7,6,7,8,7,8,9 diurutkan menjadi 5,6,6,7,7,7,8,8,9

Mencari Median atau nilai tengah

5,6,6,7,7,7,8,8,9

Median adalah nilai tengah setelah data diurutkan dari yang terkecil sampai terbesar jika banyaknya data ganjil maka ambil nilai tengah jika jumlah datanya genap maka kita ambil dua nilai ditengah kemudian dibagi dua, dari soal  diatas karena jumlah datanya ganjil maka bisa kita ambil nilai tengahnya adalah 7, jadi nilai mediannya adalah 7.

Sebuah buku kecil memiliki 12 halaman dengan jumlah kata sebagai berikut: 271, 354, 296, 301, 333, 326, 285, 298, 327, 316, 287 dan 314.
Berapa jumlah median kata per halaman?

Jawaban:

Urutkan nomor halaman terlebih dahulu: 271, 285, 287, 296, 298, 301, 314, 316, 326, 327, 333, 354

Ada dua angka di tengah: 301 dan 314

Rata-rata 301 dan 314 adalah (301 + 314) / 2 = 615/2 = 307.5

Jadi jumlah median kata adalah 307,5

Keluarga Budi melewati 7 negara bagian pada liburan musim panas. Harga Bensin berbeda dari satu negara bagian ke negara bagian lain. Hitung median biaya bensin!

1,79, 1,61, 2,09, 1,84, 1,96, 2,11, 1,75

Jawaban:

Dengan mengatur data dari terkecil hingga terbesar, kita mendapatkan:

1.61, 1.75, 1.79, 1.84, 1.96, 2.09, 2.11

Oleh karena itu, median biaya bensin adalah 1,84. Ada tiga negara bagian dengan biaya bensin lebih besar dan 3 dengan harga lebih kecil.

Data π = 3.141592653589793238462643383…
Berapa median dari 12 digit pertama π?

Jawaban:

12 digit pertama π adalah 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8
Urutkan ini sesuai ukurannya:
1, 1, 2, 3, 3, 4, 5, 5, 5, 6, 8, 9

Median adalah mean dari dua bilangan tengah = (4 + 5) / 2 = 9/2 = 4,5

Baca juga ? Nilai Pi 3,14 atau 22/7 atau 355/113 – Rumus dengan Pi & Contoh Soal dan Jawaban

Dari lima kali kuis statistika, seorang mahasiswa memperoleh nilai 82, 93, 86, 92, dan 79. Tentukan median populasi ini!

Jawaban:

Setelah data disusun dari yang terkecil sampai terbesar, diperoleh  79 82 86 92 93

Oleh karena itu mediannya adalah 86.

Baca juga ? Statistika Matematika – Rumus, Contoh Soal dan Jawaban

Sepuluh orang siswa sekolah dijadikan sampel dan dihitung tinggi badannya. Hasil pengukuran tinggi badan kesepuluh siswa tersebut adalah sebagai berikut: 172, 167, 180, 171, 169, 160, 175, 173, 170, 165.
Hitunglah median dari data tinggi badan siswa!

Hasil ulangan mata pelajaran Matematika yang didapat dari salah seorang murid selama 1 semester adalah: 7.5, 8, 7, 6.5, 7, 7, 6.5, 8, 7.5, 8, 7, 7. Berapakah nilai median dari data tunggal di atas?

Jawaban:

Untuk menghitungnya, maka kita harus mengurutkan data terlebih dahulu mulai dari yang terkecil hingga terbesar, maka didapatkan data sebagai berikut:

6.5, 6.5, 7, 7, 7, 7, 7, 7.5, 7.5, 8, 8, 8

Setelah itu, dilanjutkan dengan mencari nilai tengah dari data yang sudah diurutkan. Jumlah data di atas ada 12 (genap), jadi nilai tengahnya ada dua, yaitu 7 dan 7

= (7+7) : 2
=14 : 2
= 7

Bacaan Lainnya

• Statistika Matematika – Rumus, Contoh Soal dan Jawaban
• Nilai Pi 3,14 atau 22/7 atau 355/113 – Rumus dengan Pi – Contoh Soal dan Jawaban
• Faktorial Matematika Beserta Contoh Soal dan Jawaban
• Teorema Rolle Matematika Beserta Contoh Soal dan Jawaban (Kalkulus)
• Deret Taylor Matematika dan Teorema Taylor Bersama Contoh Soal dan Jawaban (Kalkulus)
• Deret Pangkat Matematika Beserta Contoh Soal dan Jawaban (Kalkulus)
• Rumus Limit Fungsi Matematika Kalkulus Beserta Contoh Soal dan Jawaban
• Fungsi Matematika: Linear, Konstan, Identitas – Beserta Soal dan Jawaban
• Topologi Matematika – Contoh Soal dan Jawaban Ruang Topologi
• Rumus Matematika Keuangan – Contoh Soal dan Jawaban
• Induksi Matematika Rumus, Pembuktian, Deret, Keterbagian, Pertidaksamaan, Soal, Pembahasan dan Jawaban
• Jenis dan Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
• Berapa Kecerdasan IQ Anda? Tes IQ Anda Disini
• Bidang-Bidang Matematika: Besaran, Ruang, Perubahan, Struktur, Dasar dan Filsafat, Diskret, Terapan
• 10 Cara Belajar Pintar, Efektif, Cepat Dan Mudah Di Ingat – Untuk Ulangan & Ujian Pasti Sukses!
• Tulisan Menunjukkan Kepribadian Anda & Bagaimana Cara Anda Menulis?
• Penyakit yang dapat dicegah dengan vaksin – Wajib diketahui
• Top 10 Sungai Terpanjang Di Dunia
• Tempat Wisata Yang Wajib Dikunjungi Di Indonesia Dan Luar Negri
• Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
• Bentuk Kaki Menandakan Karakter Anda – Bentuk Kaki nomer berapa yang Anda miliki?

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

• HP Android
• HP iOS (Apple)

Sumber bacaan: By Jus

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing