PINTERpandai
Pinter Pandai

Pertidaksamaan Matematika: Linear, Kuadrat, Akar, Pecahan, Mutlak – Contoh Soal dan Jawaban

6 min read

Pertidaksamaan matematika 2

Pertidaksamaan Matematika adalah

Pertidaksamaan dalam matematika adalah kalimat/pernyataan matematika yang menunjukkan perbandingan ukuran dua objek atau lebih.

Notasi tanda pertidaksamaan matematika

NotasiArtiContoh
 <lebih kecil
kurang dari		2 < 3
x + 1 < 3
 >lebih besar
lebih dari		3 > 2
3x + 1 > 5
 ≤lebih kecil atau sama dengan
batas dibawah
maksimum
maksimal
sebanyaknya
paling banyak
tidak lebih dari
sekurangnya		2 ≤ 3
x + 1 ≤ 3
 ≥lebih besar atau sama dengan
batas diatas
minimum
minimal
sesedikitnya
paling sedikit
tidak kurang dari
selebihnya		3 ≥ 2
3x + 1 ≥ 5
 ≠tidak sama dengan2 ≠ 3
x + 1 ≠ 3
 a < x < bdiantara a dan b2 < x < 5
 a ≤ x < bdiantara a dan b bila nilai minimal a2 ≤ x < 5
 a < x ≤ bdiantara a dan b bila maksimal b2 < x ≤ 5
 a ≤ x ≤ bdiantara a dan b bila minimal a dan maksimal b2 ≤ x ≤ 5

Jenis-jenis pertidaksamaan matematika

1. Pertidaksamaan Linear

  • Tentukan nilai x dari pertidaksamaan  {\displaystyle 6x-7<5x+3}!
{\displaystyle 6x-7<5x+3}
{\displaystyle 6x-5x<3+7}
{\displaystyle x<10}
{\displaystyle HP=\{x|x<10,x\in R\}}
  • Tentukan nilai x dari pertidaksamaan {\displaystyle 5-2x\geq 4x-1}!
{\displaystyle 5-2x\geq 4x-1}
{\displaystyle -2x-4x\geq -1-5}
{\displaystyle -6x\geq -6} (karena nilai negatif maka tanda harus terbalik)
{\displaystyle x\leq 1}
{\displaystyle HP=\{x|x\leq 1,x\in R\}}

2. Pertidaksamaan Kuadrat

  • Tentukan nilai x dari pertidaksamaan {\displaystyle x^{2}-7x>10-4x}!
{\displaystyle x^{2}-7x>10-4x}
{\displaystyle x^{2}-3x-10>0}

dibuat dengan harga nol

{\displaystyle x^{2}-3x-10=0}
{\displaystyle (x+2)(x-5)=0}
{\displaystyle x=-2\lor x=5}

dibuat irisan

-25
+++N/A—-N/A+++
{\displaystyle HP=\{x|x<-2\lor x>5,x\in R\}}
  • Tentukan nilai x dari pertidaksamaan {\displaystyle 2-x^{2}\leq x-10}!
{\displaystyle 2-x^{2}\leq x-10}
{\displaystyle x^{2}+x-12\geq 0}

dibuat harga nol

{\displaystyle x^{2}+x-12=0}
{\displaystyle (x+4)(x-3)=0}
{\displaystyle x=-4\lor x=3}

dibuat irisan

(-4)(3)
+++N/A—-N/A+++
{\displaystyle HP=\{x|x\leq -4\lor x\geq 3,x\in R\}}

3. Pertidaksamaan Akar

Dalam bentuk pertidaksamaan akar sebagai berikut:

{\displaystyle {\sqrt {f(x)}}<0} atau {\displaystyle {\sqrt {f(x)}}>0}

haruslah mempunyai syarat yaitu f(x) ≥ 0.

  • Tentukan nilai x dari pertidaksamaan {\displaystyle {\sqrt {x^{2}-4x}}<{\sqrt {10-x}}}!
{\displaystyle {\sqrt {x^{2}-4x}}<{\sqrt {10-x}}}
{\displaystyle ({\sqrt {x^{2}-4x}})^{2}<({\sqrt {10-x}})^{2}}
{\displaystyle x^{2}-4x<10-x}
{\displaystyle x^{2}-3x-10<0}

dibuat harga nol

{\displaystyle x^{2}-3x-10=0}
{\displaystyle (x+2)(x-5)=0}
{\displaystyle x=-2\lor x=5}

dibuat irisan

-25
+++N/A—-N/A+++
{\displaystyle -2<x<5}

karena ada syarat akar maka:

akar 1
{\displaystyle x^{2}-4x\geq 0}

dibuat harga nol

{\displaystyle x^{2}-4x=0}
{\displaystyle x(x-4)=0}
{\displaystyle x=0\lor x=4}

dibuat irisan

04
+++N/A—-N/A+++
{\displaystyle x\leq 0\lor x\geq 4}
akar 2
{\displaystyle 10-x\geq 0}
{\displaystyle x\leq 10}

gabungkan umum dan syarat

irisan-2(0)(4)5(10)
pertamatidakN/AyaN/AyaN/AyaN/AtidakN/Atidak
keduayaN/AyaN/AtidakN/AyaN/AyaN/Aya
ketigayaN/AyaN/AyaN/AyaN/AyaN/Atidak
{\displaystyle HP=\{x|-2<x\leq 0\lor 4\leq x<5,x\in R\}}
  • Tentukan nilai x dari pertidaksamaan {\displaystyle {\sqrt {x^{2}-4}}\geq {\sqrt {3x+50}}}!
{\displaystyle {\sqrt {x^{2}-4}}\geq {\sqrt {3x+50}}}
{\displaystyle ({\sqrt {x^{2}-4}})^{2}\geq ({\sqrt {3x+50}})^{2}}
{\displaystyle x^{2}-4\geq 3x+50}
{\displaystyle x^{2}-3x-54\geq 0}

dibuat harga nol

{\displaystyle x^{2}-3x-54=0}
{\displaystyle (x+6)(x-9)=0}
{\displaystyle x=-6\lor x=9}

dibuat irisan

(-6)(9)
+++N/A—-N/A+++
{\displaystyle x\leq -6\lor x\geq 9}

karena ada syarat akar maka:

akar 1
{\displaystyle x^{2}-4\geq 0}

dibuat harga nol

{\displaystyle x^{2}-4=0}
{\displaystyle (x+2)(x-2)=0}
{\displaystyle x=-2\lor x=2}

dibuat irisan

(-2)(2)
+++N/A—-N/A+++
{\displaystyle x\leq -2\lor x\geq 2}
akar 2
{\displaystyle 3x+50\geq 0}
{\displaystyle x\geq -{\frac {50}{3}}}

gabungkan umum dan syarat

irisan(-50/3)(-6)(-2)(2)(9)
pertamayaN/AyaN/AtidakN/AtidakN/AtidakN/Aya
keduayaN/AyaN/AyaN/AtidakN/AyaN/Aya
ketigatidakN/AyaN/AyaN/AyaN/AyaN/Aya
{\displaystyle HP=\{x|2<x\leq 0\lor 4\leq x<5,x\in R\}}

4. Pertidaksamaan Pecahan

Dalam bentuk pertidaksamaan pecahan sebagai berikut:

{\displaystyle {\frac {f(x)}{g(x)}}<0} atau {\displaystyle {\frac {f(x)}{g(x)}}>0}

haruslah mempunyai syarat yaitu penyebut atau g(x) ≠ 0.

  • Tentukan nilai x dari pertidaksamaan {\displaystyle {\frac {x-4}{x-3}}<{\frac {x+1}{x-2}}}!
{\displaystyle {\frac {x-4}{x-3}}<{\frac {x+1}{x-2}}}
{\displaystyle {\frac {x-4}{x-3}}-{\frac {x+1}{x-2}}<0}
{\displaystyle {\frac {(x-4)(x-2)-(x+1)(x-3)}{(x-3)(x-2)}}<0}
{\displaystyle {\frac {(x^{2}-6x+8)-(x^{2}-2x-3)}{(x-3)(x-2)}}<0}
{\displaystyle {\frac {-4x+11}{(x-3)(x-2)}}<0}
{\displaystyle -4x+11<0}
{\displaystyle x<{\frac {11}{4}}}

karena ada syarat pecahan maka:

penyebut 1
{\displaystyle x-3\neq 0}
{\displaystyle x\neq 3}
penyebut 2
{\displaystyle x-2\neq 0}
{\displaystyle x\neq 2}

dibuat irisan

211/43
+++N/A—-N/A+++N/A—-
{\displaystyle HP=\{x|2<x<{\frac {11}{4}}\lor x>3,x\in R\}}
  • Tentukan nilai x dari pertidaksamaan {\displaystyle {\frac {x+6}{x+17}}\geq {\frac {1}{x-3}}}!
{\displaystyle {\frac {x+6}{x+17}}\geq {\frac {1}{x-3}}}
{\displaystyle {\frac {x+6}{x+17}}-{\frac {1}{x-3}}\geq 0}
{\displaystyle {\frac {(x+6)(x-3)-(x+17)}{(x+17)(x-3)}}\geq 0}
{\displaystyle {\frac {x^{2}+3x-18-x-17}{(x+17)(x-3)}}\geq 0}
{\displaystyle {\frac {x^{2}+2x-35}{(x-3)(x-2)}}\geq 0}
{\displaystyle x^{2}+2x-35\geq 0}

dibuat harga nol

{\displaystyle x^{2}+2x-35=0}
{\displaystyle (x+7)(x-5)=0}
{\displaystyle x=-7\lor x=5} (tanpa gambar irisan)

karena ada syarat pecahan maka:

penyebut 1
{\displaystyle x+17\neq 0}
{\displaystyle x\neq -17}
penyebut 2
{\displaystyle x-3\neq 0}
{\displaystyle x\neq 3}

dibuat irisan

-17(-7)3(5)
+++N/A—-N/A+++N/A—-N/A+++
{\displaystyle HP=\{x|x<-17\lor -7\leq x<3\lor x\geq 5,x\in R\}}

5. Pertidaksamaan Mutlak

Dalam bentuk pertidaksamaan mutlak adalah sebagai berikut:

{\displaystyle |f(x)|>g(x)}

haruslah mempunyai dua nilai yaitu

{\displaystyle |f(x)|=\left\{{\begin{matrix}|f(x)|<g(x),&{\mbox{maka penyelesaian}}-g(x)<f(x)<g(x)\\\\|f(x)|>g(x),&{\mbox{maka penyelesaian}}f(x)<-g(x)\lor f(x)>g(x)\end{matrix}}\right.}

Pertidaksamaan mutlak akan memungkinkan definit + dan – karena tidak memotong dan menyinggung sumbu y.

  • Tentukan nilai x dari pertidaksamaan {\displaystyle |x^{2}+x|<12}!
{\displaystyle |x^{2}+x|<12}

karena f(x) < g(x) maka penyelesaian -g(x) < f(x) < g(x)

{\displaystyle -12<x^{2}+x<12}
untuk {\displaystyle -12<x^{2}+x}
{\displaystyle -12<x^{2}+x}
{\displaystyle x^{2}+x+12>0} definit +
untuk {\displaystyle x^{2}+x<12}
{\displaystyle x^{2}+x<12}
{\displaystyle x^{2}+x-12<0}

dibuat harga nol

{\displaystyle x^{2}+x-12=0}
{\displaystyle (x+4)(x-3)<0}
{\displaystyle x=-4\lor x=3}

dibuat irisan

-43
+++N/A—-N/A+++
{\displaystyle -4<x<3}
{\displaystyle HP=\{x|-4<x<3,x\in R\}}
  • Tentukan nilai x dari persamaan {\displaystyle |x^{2}-4x-12|-|7-6x|\geq 5}!
terlebih dahulu untuk mempunyai batas-batas yang ada
untuk | x^2 – 4x – 12 |
{\displaystyle |x^{2}-4x-12|=\left\{{\begin{matrix}x^{2}-4x-12,&{\mbox{maka penyelesaian}}x^{2}-4x-12\geq 0\\\\-(x^{2}-4x-12),&{\mbox{maka penyelesaian}}x^{2}-4x-12<0\end{matrix}}\right.}
batasan f(x)
{\displaystyle x^{2}-4x-12\geq 0}

dibuat harga nol

{\displaystyle x^{2}-4x-12=0}
{\displaystyle (x+2)(x-6)=0}
{\displaystyle x=-2\lor x=6}

dibuat irisan

-26
+++N/A—-N/A+++
{\displaystyle x\leq -2\lor x\geq 6}
batasan -f(x)
{\displaystyle x^{2}-4x-12<0}

dibuat harga nol

{\displaystyle x^{2}-4x-12=0}
{\displaystyle (x+2)(x-6)=0}
{\displaystyle x=-2\lor x=6}

dibuat irisan

-26
+++N/A—-N/A+++
{\displaystyle -2<x<6}
untuk | 7 – 6x |
{\displaystyle |7-6x|=\left\{{\begin{matrix}7-6x,&{\mbox{maka penyelesaian}}7-6x\geq 0\\\\-(7-6x),&{\mbox{maka penyelesaian}}7-6x<0\end{matrix}}\right.}
batasan f(x)
{\displaystyle 7-6x\geq 0}
{\displaystyle x\leq {\frac {7}{6}}}
batasan -f(x)
{\displaystyle 7-6x<0}
{\displaystyle x>{\frac {7}{6}}}

keempat batas-batas akan dibuat irisan

irisan-27/66
pertamax^2 – 4x – 12N/AN/AN/Ax^2 – 4x – 12
keduaN/A-(x^2 – 4x – 12)N/A-(x^2 – 4x – 12)N/A
ketiga7 – 6xN/A7 – 6xN/AN/A
keempatN/AN/A-(7 – 6x)N/A-(7 – 6x)
untuk x <= -2
{\displaystyle x^{2}-4x-12-(7-6x)\geq 5}
{\displaystyle x^{2}-4x-12-7+6x-5\geq 0}
{\displaystyle x^{2}+2x-24\geq 0}

dibuat harga nol

{\displaystyle x^{2}+2x-24=0}
{\displaystyle (x+6)(x-4)=0}
{\displaystyle x=-6\lor x=4}

dibuat irisan

(-6)(-2)(4)
YaN/AYaN/ATidakN/ATidak
+++N/A—-N/A—-N/A+++
{\displaystyle x\leq -6}
untuk -2 < x <= 7/6
{\displaystyle -(x^{2}-4x-12)-(7-6x)\geq 5}
{\displaystyle -x^{2}+4x+12-7+6x-5\geq 0}
{\displaystyle x^{2}-10x\leq 0}

dibuat harga nol

{\displaystyle x^{2}-10x=0}
{\displaystyle x(x-10)=0}
{\displaystyle x=0\lor x=10}

dibuat irisan

-2(0)(7/6)(10)
TidakN/AYaN/AYaN/ATidakN/ATidak
+++N/A+++N/A—-N/A—-N/A+++
{\displaystyle 0\leq x\leq {\frac {7}{6}}}
untuk 7/6 < x < 6
{\displaystyle -(x^{2}-4x-12)-(-(7-6x))\geq 5}
{\displaystyle -x^{2}+4x+12+7-6x-5\geq 0}
{\displaystyle x^{2}+2x\leq 0}

dibuat harga nol

{\displaystyle x^{2}+2x=0}
{\displaystyle x(x+2)=0}
{\displaystyle x=0\lor x=-2}

dibuat irisan

(-2)(0)7/66
TidakN/ATidakN/ATidakN/AYaN/ATidak
+++N/A—-N/A+++N/A+++N/A+++
{\displaystyle \varnothing }

untuk x >= 6

{\displaystyle x^{2}-4x-12-(-(7-6x))\geq 5}
{\displaystyle x^{2}-4x-12+7-6x-5\geq 0}
{\displaystyle x^{2}-10x-10\geq 0} definit +
{\displaystyle \varnothing }
{\displaystyle HP=\{x|x\leq -6\lor 0\leq x\leq {\frac {7}{6}},x\in R\}}

gabungkan ketiga batas-batas. jadi:

{\displaystyle HP=\{x|-{\frac {11}{5}}\leq x<-{\frac {4}{3}}\lor -{\frac {4}{3}}\leq x\leq 3,x\in R\}}
{\displaystyle HP=\{x|-{\frac {11}{5}}\leq x\leq 3,x\in R\}}
  • Tentukan nilai x dari pertidaksamaan {\displaystyle |{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|}!
{\displaystyle |{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|}
{\displaystyle ({\frac {x+4}{10-x}})^{2}<({\frac {1}{x-2}})^{2}}
{\displaystyle ({\frac {x+4}{10-x}})^{2}-({\frac {1}{x-2}})^{2}<0}
{\displaystyle ({\frac {x+4}{10-x}}+{\frac {1}{x-2}})({\frac {x+4}{10-x}}-{\frac {1}{x-2}})<0}
{\displaystyle ({\frac {(x+4)(x-2)+10-x}{(10-x)(x-2)}})({\frac {(x+4)(x-2)-(10-x)}{(10-x)(x-2)}})<0}
{\displaystyle ({\frac {x^{2}+2x-8+10-x}{(10-x)(x-2)}})({\frac {x^{2}+2x-8-10+x}{(10-x)(x-2)}})<0}
{\displaystyle ({\frac {x^{2}+x+2}{(10-x)(x-2)}})({\frac {x^{2}+3x-18}{(10-x)(x-2)}})<0}
akar dari {\displaystyle {\frac {x^{2}+x+2}{(10-x)(x-2)}}}
{\displaystyle {\frac {x^{2}+x+2}{(10-x)(x-2)}}<0}
{\displaystyle x^{2}+x+2=0} definit +

karena ada syarat pecahan maka:

penyebut 1
{\displaystyle 10-x\neq 0}
{\displaystyle x\neq 10}
penyebut 2
{\displaystyle x-2\neq 0}
{\displaystyle x\neq 2}
akar dari {\displaystyle {\frac {x^{2}+3x-18}{(10-x)(x-2)}}}
{\displaystyle {\frac {x^{2}+3x-18}{(10-x)(x-2)}}<0}
{\displaystyle x^{2}+3x-18<0}

dibuat harga nol

{\displaystyle x^{2}+3x-18=0}
{\displaystyle (x+6)(x-3)=0}
{\displaystyle x=-6\lor x=3} (tanpa gambar irisan)

karena ada syarat pecahan maka:

penyebut 1
{\displaystyle 10-x\neq 0}
{\displaystyle x\neq 10}
penyebut 2
{\displaystyle x-2\neq 0}
{\displaystyle x\neq 2}

dibuat irisan

-62*310*
+++N/A—-N/A—-N/A+++N/A+++
nb: * = mempunyai 2 akar
{\displaystyle HP=\{x|-6<x<3,x\in R\}}
  • Tentukan nilai x dari pertidaksamaan {\displaystyle |{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|}{\displaystyle |{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|}!
{\displaystyle |{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|}
{\displaystyle ({\sqrt {x^{2}-4x}})^{2}\geq ({\sqrt {3x-10}})^{2}}
{\displaystyle x^{2}-4x\geq 3x-10}
{\displaystyle x^{2}-7x+10\geq 0}

dibuat harga nol

{\displaystyle x^{2}-7x+10=0}
{\displaystyle (x-2)(x-5)=0}
{\displaystyle x=2\lor x=5}

dibuat irisan

25
+++N/A—-N/A+++
{\displaystyle x\leq 2\lor x\geq 5}

karena ada syarat akar maka:

akar 1
{\displaystyle x^{2}-4x\geq 0}

dibuat harga nol

{\displaystyle x^{2}-4x=0}
{\displaystyle x(x-4)=0}
{\displaystyle x=0\lor x=4}

dibuat irisan

04
+++N/A—-N/A+++
{\displaystyle x\leq 0\lor x\geq 4}
akar 2
{\displaystyle 3x-10\geq 0}
{\displaystyle x\geq {\frac {10}{3}}}

gabungkan umum dan syarat

irisan(0)(2)(10/3)(4)(5)
pertamayaN/AyaN/AtidakN/AtidakN/AtidakN/Aya
keduayaN/AtidakN/AtidakN/AtidakN/AyaN/Aya
ketigatidakN/AtidakN/AtidakN/AyaN/AyaN/Aya
{\displaystyle HP=\{x|x\geq 5,x\in R\}}
Pertidaksamaan matematika 2
Pertidaksamaan Matematika: Linear, Kuadrat, Akar, Pecahan, Mutlak

Contoh Soal dan Jawaban Pertidaksamaan Matematika

1. Jika diketahui a² + b² = 1 dan c² + d² = 1. Berapa nilai minimum ac + bd – 2?

Jawaban pertidaksamaan matematika:

Untuk setiap bilangan real a, b, c, dan d terdapat hubungan

(a+c)² ≥ 0 → a² + c² + 2ac ≥ 0    (1)
(b+d)² ≥ 0 → b² + d² + 2bd ≥ 0  (2)

Jumlahkan persamaan (1) dan (2)

(a²+b²) + c²+d²) + 2(ac + bd) ≥ 0
1+1+2(ac + bd) ≥ 0
ac + ad ≥ -1  (kurangi kedua ruas dengan 2)
∴ ac + bd – 2 ≥ -3

dari bentuk pertidaksamaan terakhir bisa diambil kesimpulan bahwa nilai ac + bd – 2 mempunyai nilai minimum -3.

2. Nilai y yang memenuhi   \dfrac{1}{y} - \dfrac{1}{y-1} < 1

a)  0<y<1
b)  0<y \le 1
c)  y<0 atau y \ge 1
d)  y \le 0 atau y >1
e)  y < 0 atau y > 1

Jawaban:

\displaystyle \begin{aligned} \frac{1}{y}-\frac{1}{y-1}-1 &< 0 \\ \end{aligned}

dengan menyamakan penyebut didapat

\displaystyle \begin{aligned} \frac{y-1}{y(y-1)}-\frac{y}{y(y-1)}-\frac{y(y-1)}{y(y-1)} &< 0 \\ \frac{-y^2+y-1}{y(y-1)} &< 0 \\ \end{aligned}

Pembilang merupakan bentuk definit negatif (D < 0 dan a < 0) jadi berapapun nilai y yang dipilih akan tetap bernilai negatif.

Anda dapat menggunakan bantuan dengan garis bilangan:

Pertidaksamaan matematika nilai y

Jadi nilai y yang memenuhi

y < 0 atau y > 1

Cara alternatif atau cara ke dua:

Dari soal bisa diambil kesimpulan bahwa y \neq 0 dan y \neq 1, karena akan menyebabkan pembagian dengan nol. Jadi semua pilhan yang mengandung 0 dan 1 pasti salah.
Akibatnya yang masih mungkin benar adalah pilihan A dan E.

Pilih y = 2 yang akan menyebabkan nilai pertidaksamaan menjadi \dfrac{1}{2} - \dfrac{1}{1} < 1 merupakan pernyataan yang benar. Karena y=2 tidak termasuk dalam selang dipilhan A, tetapi ada termasuk dalam selang dipilihan E, sehingga pilihan E merupakan pilihan jawaban yang benar

3. Himpunan titik-titik yang memenuhi pertidaksamaan y - 2x > 0 dan y > 4 - x seluruhnya berada di kuadran mana?
a) I
b) II
c) I dan II
d) I dan IV
e) I, III dan IV

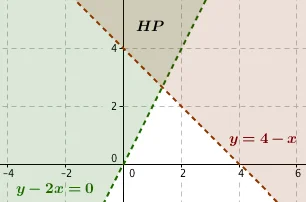
Soal himpunan titik-titik yang memenuhi pertidaksamaan matematika

Jawaban:

Himpunan penyelesaian dari sistem pertidaksamaan berada di kuadran I dan II. Jawaban yang benar: c) I dan II.

4. Banyaknya bilangan real a agar pertidaksamaan |x² + 2ax +3a| ≤ 2 mempunyai tepat satu solusi pada x adalah…

Jawaban:

\displaystyle \begin{aligned} |x^2+2ax+3a|&\le 2 &~~~~~\text{(kuadratkan kedua ruas)}\\ (x^2+2ax+3a)^2&\le 2^2\\ (x^2+2ax+3a)^2-2^2&\le 0&~~~~~\text{(faktorkan)}\\ \{(x^2+2ax+3a)+2\}\{(x^2+2ax+3a)-2\}&\le 0\\ (x^2+2ax+3a+2)(x^2+2ax+3a-2)&\le 0\\ \end{aligned}

Supaya penyelesaian mempunyai tepat satu solusi maka setiap faktor harus mempunyai nilai D=0

(1) x^2+2ax+3a+2 :

\displaystyle \begin{aligned} (2a)^2-4(1)(3a+2)&=0\\ a^2-3a-2&=0 ~~~~~ ...\:(D_1)\\ \therefore\: a_1&=\tfrac{1}{2}\left(3+\sqrt{17}\right)\:\cup\: a_2=\tfrac{1}{2}\left(3-\sqrt{17}\right)\\ \end{aligned}

(2) x^2+2ax+3a-2 :

\displaystyle \begin{aligned} (2a)^2-4(1)(3a-2)&=0\\ a^2-3a+2&=0\\ (a-1)(a-2)&=0 ~~~~~ ...\:(D_2)\\ \therefore\: a_3&=1\:\cup\: a_4=2\\ \end{aligned}

Karena dari kedua faktor itu memberikan nilai a yang berbeda, lakukan cek silang nilai diskriminan dari a

\displaystyle \begin{array}{ll} a_1=\tfrac{1}{2}\left(3-\sqrt{17}\right) &\rightarrow D_2 > 0\\ a_2=\tfrac{1}{2}\left(3+\sqrt{17}\right) &\rightarrow D_2 > 0\\ a_3=1&\rightarrow D_1 < 0\\ a_4=2&\rightarrow D_1 < 0 \end{array}

Nilai a_1 dan a_2 akar dari faktor (1) menyebabkan nilai D_2>0 akibatnya akan membuat faktor (2) mempunyai akar yang lain (tidak memenuhi syarat tepat satu akar).

Nilai a_3 dan a_4 akar dari faktor (2) menyebabkan nilai D_1<0 (definit positif) akibatnya faktor (1) tidak akan mempunyai akar lain.

Jadi banyaknya bilangan riil a yang memembuat pertidaksamaan hanya mempunyai tepat satu solusi ada 2 yaitu a=1 atau a=2.

Dengan menggunakan ilustrasi grafik

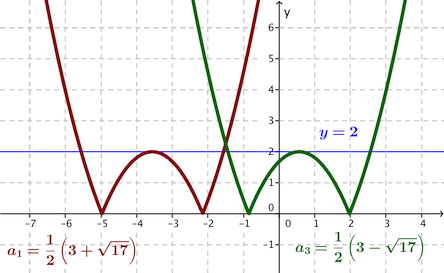
Ilustrasi grafik pertidak samaan 1

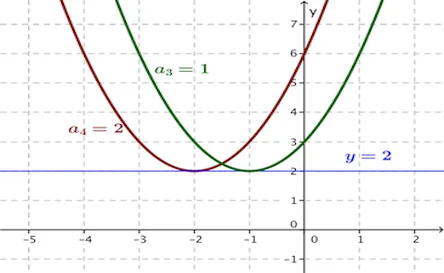
Ilustrasi grafik pertidak samaan 2

catatan:
Persamaan kuadrat ax^2+bx+c=0 mempunyai tepat satu solusi/jawaban jika
\boxed{~D=0~}
dimana:
\boxed{~D=b^2-4ac~}

5. Semua nilai x yang memenuhi (2x+1)(x-1)\le(x-1)
a)  x\le 1
b)  x\ge 0
c)  x\ge \frac{1}{2}
d)  \frac{1}{2}\le x\le 1
e)  0\le x\le 1

Jawaban:

\displaystyle \begin{aligned} (2x+1)(x-1)&\le (x-1)\\ (2x+1)(x-1)-(x-1)&\le 0\\ 2x^2-2x&\le 0\\ 2x(x-1)&\le 0 \end{aligned}

Semua nilai x yang memenuhi pertidaksamaan

Jadi nilai x yang memenuhi 0\le x\le 1

Cara Alternatif :

\displaystyle \begin{array}{lclr} x=0 &\rightarrow &(1)(-1) \le -1 &\text{(Benar)}\\ x=-1&\rightarrow &(-1)(-2) \le -2 &\text{(Salah)}\\ x=2&\rightarrow &(5)(1)\le 1 &\text{(Salah)} \end{array}

Kesimpulannya: pilihan yang paling cocok E

6. Himpunan penyelesaian dari \displaystyle \sqrt{2x+2}-\sqrt{6x-8}\ge 0 adalah…

Jawaban:

\displaystyle \begin{aligned} \sqrt{2x+2}-\sqrt{6x-8}&\ge 0\\ \sqrt{2x+2}&\ge 0\sqrt{6x-8}&~~~~~\text{(kuadratkan kedua ruas)}\\ 2x+2&\ge 6x-8\\ x&\le\frac{5}{2} \end{aligned}

Syarat (1) 2x+2\ge 0\:\rightarrow\:x\ge -1

Syarat (2) 6x-8\ge 0\:\rightarrow\:x\ge \dfrac{4}{3}

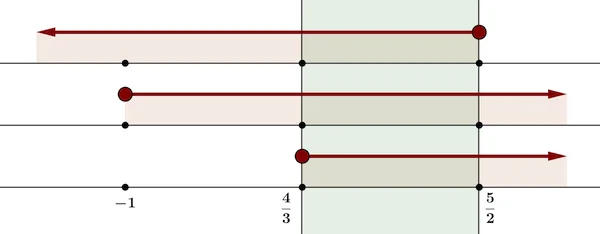
Himpunan penyelesaian pertidaksamaan matematika

Cara Alternatif:
Cek pilihan

x=0\:\rightarrow\: \sqrt{0}\ge\sqrt{-8} ~~~~~\text{(Salah)}
ket: dalam akar tidak boleh negatif. Akibatnya pilihan A dan C pasti salah.

x=3\:\rightarrow\: \sqrt{8}\ge\sqrt{10} ~~~~~\text{(Salah)}
ket: Pilihan B dan D pasti salah, jadi pilihan yang benar adalah E

7. Berapa bilangan bulan terdekat dengan y2 jika y adalah bilangan real sehingga 3 < y < 4 dan y3 - 6y - 7 = 0?

Jawaban:

Gunakan manipulasi aljabar untuk mencari nilai y

\displaystyle \begin{aligned} y^3-6y-7&=0\\ y(y^2-6)&=7\\ y&=\frac{7}{y^2-6} \end{aligned}

Diketahui bahwa 3 < y < 4 sehingga

\displaystyle \begin{aligned} &3 < \frac{7}{y^2-6} < 4&~~~~~|\text{ : 7 }|\\ &\frac{3}{7} < \frac{1}{y^2-6} < \frac{4}{7}&~~~~~\text{(sifat kebalikan)}\\ &\frac{7}{4} < y^2-6 < \frac{7}{3}&~~~~~|\text{ + 6 }|\\ &7\tfrac{3}{4} < y^2 < 8\tfrac{1}{3} \end{aligned}

Jadi bilangan bulan terdekat dengan y2 adalah 8

8.  Jika x dan y memenuhi 2y2 - 1 > x dan 9y - x + 4 = 0, maka x - y memenuhi…

a) 0 < x-y < 44

b)   -\dfrac{1}{2} < x-y < 49

c)  x-y < -\dfrac{11}{2} \text{ atau }x-y > \dfrac{99}{2}

d)  x-y < 0 \text{ atau } x - y > 44

e)  -\dfrac{1}{2}< x-y< 44

Jawaban:

Kurva 2y2 - 1 = x berupa parabola terbuka ke kanan, dan 9y - x + 4 = 0 merupakan garis lurus. Titik potong kedua kurva bisa dicari dari ..

\displaystyle \begin{aligned} &9y-x+4=0~\Leftrightarrow~x=9y-4 ~~(\text{subtitusi ke pers parabola})\\ &2y^2-1=9y-4 \\ &2y^2-9y-5=0\\ &(2y+1)(y-5)=0~\rightarrow~\therefore\:y=-\frac{1}{2}\text{ atau } 5 \end{aligned}

Untuk y = -1/2 nilai x = -1/2
Untuk y = 5 nilai x = 49
Titik potong kedua kurva di A(-1/2, 1/2) dan B(49,5)
Dari gambar di bawah terlihat bahwa himpunan penyelesaian berada pada garis 9y – x + 4 = 0 (garis tebal berpanah)

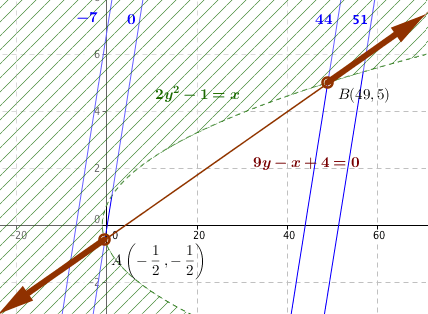
Soal himpunan penyelesaian berada pada garis 9y

Nilai x - y maksimum dan minimum terletak di titik A dan titik B.
jadi interval nilai x - y < 0 atau x - y > 44

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Math is Fun, The Free Dictionary

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing

Pinter Pandai
«
»

Quiz Tantangan Logika Matematika: Jika 6 + 4 =…

PinterPandai
Okt 14, 2024 58 sec read

Tes matematika logika: Jika 4 + 3 = 27,…

PinterPandai
Okt 9, 2024 1 min read

Nilai Pi 1 juta digit pertama | Analisis dan…

PinterPandai
Mei 8, 2024 1 min read

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *