PINTERpandai
Pinter Pandai

Integral Trigonometri – Fungsi Beserta Contoh Soal dan Jawaban

3 min read

Integral trigonometri

Daftar integral dari fungsi trigonometri

Daftar integral trigonometri (antiderivatif: integral tak tentu) dari fungsi trigonometri. Untuk antiderivatif yang melibatkan baik fungsi eksponensial dan trigonometri, lihat Daftar integral dari fungsi eksponensial. Untuk daftar lengkap fungsi-fungsi antiderivatif, lihat Tabel integral. Untuk antiderivatif khusus yang melibatkan fungsi trigonometri.

Umumnya, jika fungsi {\displaystyle \sin(x)} adalah suatu fungsi trigonometri, dan {\displaystyle \cos(x)} adalah turunannya,

{\displaystyle \int a\cos nx\;\mathrm {d} x={\frac {a}{n}}\sin nx+C}

Dalam semua rumus, konstanta a diasumsikan bukan nol, dan C melambangkan konstanta integrasi.

Integral trigonometri – Integrand melibatkan hanya sinus

{\displaystyle \int [fusion_builder_container hundred_percent=
{\displaystyle \int \sin ^{2}{ax}\;\mathrm {d} x={\frac {x}{2}}-{\frac {1}{4a}}\sin 2ax+C={\frac {x}{2}}-{\frac {1}{2a}}\sin ax\cos ax+C\!}
{\displaystyle \int \sin ^{3}{ax}\;\mathrm {d} x={\frac {\cos 3ax}{12a}}-{\frac {3\cos ax}{4a}}+C\!}
{\displaystyle \int x\sin ^{2}{ax}\;\mathrm {d} x={\frac {x^{2}}{4}}-{\frac {x}{4a}}\sin 2ax-{\frac {1}{8a^{2}}}\cos 2ax+C\!}
{\displaystyle \int x^{2}\sin ^{2}{ax}\;\mathrm {d} x={\frac {x^{3}}{6}}-\left({\frac {x^{2}}{4a}}-{\frac {1}{8a^{3}}}\right)\sin 2ax-{\frac {x}{4a^{2}}}\cos 2ax+C\!}
{\displaystyle \int \sin [fusion_builder_container hundred_percent=
{\displaystyle \int \sin ^{n}{ax}\;\mathrm {d} x=-{\frac {\sin ^{n-1}ax\cos ax}{na}}+{\frac {n-1}{n}}\int \sin ^{n-2}ax\;\mathrm {d} x\qquad {\mbox{(for }}n>0{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{\sin ax}}={\frac {1}{a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\mathrm {d} x}{\sin ^{n}ax}}={\frac {\cos ax}{a(1-n)\sin ^{n-1}ax}}+{\frac {n-2}{n-1}}\int {\frac {\mathrm {d} x}{\sin ^{n-2}ax}}\qquad {\mbox{(for }}n>1{\mbox{)}}\,\!}
{\displaystyle \int x\sin ax\;\mathrm {d} x={\frac {\sin ax}{a^{2}}}-{\frac {x\cos ax}{a}}+C\,\!}
{\displaystyle \int x^{n}\sin ax\;\mathrm {d} x=-{\frac {x^{n}}{a}}\cos ax+{\frac {n}{a}}\int x^{n-1}\cos ax\;\mathrm {d} x=\sum _{k=0}^{2k\leq n}(-1)^{k+1}{\frac {x^{n-2k}}{a^{1+2k}}}{\frac {n!}{(n-2k)!}}\cos ax+\sum _{k=0}^{2k+1\leq n}(-1)^{k}{\frac {x^{n-1-2k}}{a^{2+2k}}}{\frac {n!}{(n-2k-1)!}}\sin ax\qquad {\mbox{(for }}n>0{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\sin ax}{x}}\mathrm {d} x=\sum _{n=0}^{\infty }(-1)^{n}{\frac {(ax)^{2n+1}}{(2n+1)\cdot (2n+1)!}}+C\,\!}
{\displaystyle \int {\frac {\sin ax}{x^{n}}}\mathrm {d} x=-{\frac {\sin ax}{(n-1)x^{n-1}}}+{\frac {a}{n-1}}\int {\frac {\cos ax}{x^{n-1}}}\mathrm {d} x\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{1\pm \sin ax}}={\frac {1}{a}}\tan \left({\frac {ax}{2}}\mp {\frac {\pi }{4}}\right)+C}
{\displaystyle \int {\frac {x\;\mathrm {d} x}{1+\sin ax}}={\frac {x}{a}}\tan \left({\frac {ax}{2}}-{\frac {\pi }{4}}\right)+{\frac {2}{a^{2}}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {x\;\mathrm {d} x}{1-\sin ax}}={\frac {x}{a}}\cot \left({\frac {\pi }{4}}-{\frac {ax}{2}}\right)+{\frac {2}{a^{2}}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\sin ax\;\mathrm {d} x}{1\pm \sin ax}}=\pm x+{\frac {1}{a}}\tan \left({\frac {\pi }{4}}\mp {\frac {ax}{2}}\right)+C}

Integral trigonometri – Integrand melibatkan hanya kosinus

{\displaystyle \int \cos ax\;\mathrm {d} x={\frac {1}{a}}\sin ax+C\,\!}
{\displaystyle \int \cos ^{2}{ax}\;\mathrm {d} x={\frac {x}{2}}+{\frac {1}{4a}}\sin 2ax+C={\frac {x}{2}}+{\frac {1}{2a}}\sin ax\cos ax+C\!}
{\displaystyle \int \cos ^{n}ax\;\mathrm {d} x={\frac {\cos ^{n-1}ax\sin ax}{na}}+{\frac {n-1}{n}}\int \cos ^{n-2}ax\;\mathrm {d} x\qquad {\mbox{(for }}n>0{\mbox{)}}\,\!}
{\displaystyle \int x\cos ax\;\mathrm {d} x={\frac {\cos ax}{a^{2}}}+{\frac {x\sin ax}{a}}+C\,\!}
{\displaystyle \int x^{2}\cos ^{2}{ax}\;\mathrm {d} x={\frac {x^{3}}{6}}+\left({\frac {x^{2}}{4a}}-{\frac {1}{8a^{3}}}\right)\sin 2ax+{\frac {x}{4a^{2}}}\cos 2ax+C\!}
{\displaystyle \int x^{n}\cos ax\;\mathrm {d} x={\frac {x^{n}\sin ax}{a}}-{\frac {n}{a}}\int x^{n-1}\sin ax\;\mathrm {d} x\,=\sum _{k=0}^{2k+1\leq n}(-1)^{k}{\frac {x^{n-2k-1}}{a^{2+2k}}}{\frac {n!}{(n-2k-1)!}}\cos ax+\sum _{k=0}^{2k\leq n}(-1)^{k}{\frac {x^{n-2k}}{a^{1+2k}}}{\frac {n!}{(n-2k)!}}\sin ax\!}
{\displaystyle \int {\frac {\cos ax}{x}}\mathrm {d} x=\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|ax|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\cos ax}{x^{n}}}\mathrm {d} x=-{\frac {\cos ax}{(n-1)x^{n-1}}}-{\frac {a}{n-1}}\int {\frac {\sin ax}{x^{n-1}}}\mathrm {d} x\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{\cos ax}}={\frac {1}{a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\mathrm {d} x}{\cos ^{n}ax}}={\frac {\sin ax}{a(n-1)\cos ^{n-1}ax}}+{\frac {n-2}{n-1}}\int {\frac {\mathrm {d} x}{\cos ^{n-2}ax}}\qquad {\mbox{(for }}n>1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{1+\cos ax}}={\frac {1}{a}}\tan {\frac {ax}{2}}+C\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{1-\cos ax}}=-{\frac {1}{a}}\cot {\frac {ax}{2}}+C}
{\displaystyle \int {\frac {x\;\mathrm {d} x}{1+\cos ax}}={\frac {x}{a}}\tan {\frac {ax}{2}}+{\frac {2}{a^{2}}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {x\;\mathrm {d} x}{1-\cos ax}}=-{\frac {x}{a}}\cot {\frac {ax}{2}}+{\frac {2}{a^{2}}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\cos ax\;\mathrm {d} x}{1+\cos ax}}=x-{\frac {1}{a}}\tan {\frac {ax}{2}}+C\,\!}
{\displaystyle \int {\frac {\cos ax\;\mathrm {d} x}{1-\cos ax}}=-x-{\frac {1}{a}}\cot {\frac {ax}{2}}+C\,\!}
{\displaystyle \int \cos [/fusion_text][fusion_builder_container hundred_percent=

Integral trigonometri – Integrand melibatkan hanya tangen

{\displaystyle \int \tan ax\;\mathrm {d} x=-{\frac {1}{a}}\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|\cos ax|[fusion_builder_container hundred_percent=
{\displaystyle \int \tan ^{2}{x}\,\mathrm {d} x=\tan {x}-x+C}
{\displaystyle \int \tan ^{n}ax\;\mathrm {d} x={\frac {1}{a(n-1)}}\tan ^{n-1}ax-\int \tan ^{n-2}ax\;\mathrm {d} x\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{q\tan ax+p}}={\frac {1}{p^{2}+q^{2}}}(px+{\frac {q}{a}}\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\mathrm {d} x}{\tan ax+1}}={\frac {x}{2}}+{\frac {1}{2a}}\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\mathrm {d} x}{\tan ax-1}}=-{\frac {x}{2}}+{\frac {1}{2a}}\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\tan ax\;\mathrm {d} x}{\tan ax+1}}={\frac {x}{2}}-{\frac {1}{2a}}\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|\sin ax+\cos ax|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\tan ax\;\mathrm {d} x}{\tan ax-1}}={\frac {x}{2}}+{\frac {1}{2a}}\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|\sin ax-\cos ax|[fusion_builder_container hundred_percent=

Integral trigonometri – Integrand melibatkan hanya sekan

{\displaystyle \int \sec {ax}\,\mathrm {d} x={\frac {1}{a}}\ln {\left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int \sec ^{2}{x}\,\mathrm {d} x=\tan {x}+C}
{\displaystyle \int \sec ^{3}x\,dx={\frac {1}{2}}\sec x\tan x+{\frac {1}{2}}\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int \sec ^{n}{ax}\,\mathrm {d} x={\frac {\sec ^{n-2}{ax}\tan {ax}}{a(n-1)}}\,+\,{\frac {n-2}{n-1}}\int \sec ^{n-2}{ax}\,\mathrm {d} x\qquad {\mbox{ (for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{\sec {x}+1}}=x-\tan {\frac {x}{2}}+C}

Integral trigonometri – Integrands melibatkan hanya kosekan

{\displaystyle \int csc(ax)\mathrm {d} x=-{\frac {1}{a}}\ln {\left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int \csc ^{2}{x}\,\mathrm {d} x=-\cot {x}+C}
{\displaystyle \int \csc ^{n}{ax}\,\mathrm {d} x=-{\frac {\csc ^{n-1}\left(ax\right)\cos \left(ax\right)}{a(n-1)}}\,+\,{\frac {n-2}{n-1}}\int \csc ^{n-2}{ax}\,\mathrm {d} x\qquad {\mbox{ (for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{\csc {x}+1}}=x-{\frac {2\sin {\frac {x}{2}}}{\cos {\frac {x}{2}}+\sin {\frac {x}{2}}}}+C}
{\displaystyle \int {\frac {\mathrm {d} x}{\csc {x}-1}}={\frac {2\sin {\frac {x}{2}}}{\cos {\frac {x}{2}}-\sin {\frac {x}{2}}}}-x+C}

Integral trigonometri – Integrand melibatkan hanya kotangen

{\displaystyle \int \cot ax\;\mathrm {d} x={\frac {1}{a}}\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|\sin ax|[fusion_builder_container hundred_percent=
{\displaystyle \int \cot ^{n}ax\;\mathrm {d} x=-{\frac {1}{a(n-1)}}\cot ^{n-1}ax-\int \cot ^{n-2}ax\;\mathrm {d} x\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{1+\cot ax}}=\int {\frac {\tan ax\;\mathrm {d} x}{\tan ax+1}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{1-\cot ax}}=\int {\frac {\tan ax\;\mathrm {d} x}{\tan ax-1}}\,\!}

Integral trigonometri – Integrand melibatkan sinus  dan kosinus

{\displaystyle \int {\frac {\mathrm {d} x}{\cos ax\pm \sin ax}}={\frac {1}{a{\sqrt {2}}}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\mathrm {d} x}{(\cos ax\pm \sin ax)^{2}}}={\frac {1}{2a}}\tan \left(ax\mp {\frac {\pi }{4}}\right)+C}
{\displaystyle \int {\frac {\mathrm {d} x}{(\cos x+\sin x)^{n}}}={\frac {1}{n-1}}\left({\frac {\sin x-\cos x}{(\cos x+\sin x)^{n-1}}}-2(n-2)\int {\frac {\mathrm {d} x}{(\cos x+\sin x)^{n-2}}}\right)}
{\displaystyle \int {\frac {\cos ax\;\mathrm {d} x}{\cos ax+\sin ax}}={\frac {x}{2}}+{\frac {1}{2a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\cos ax\;\mathrm {d} x}{\cos ax-\sin ax}}={\frac {x}{2}}-{\frac {1}{2a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\sin ax\;\mathrm {d} x}{\cos ax+\sin ax}}={\frac {x}{2}}-{\frac {1}{2a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|\sin ax+\cos ax\right|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\sin ax\;\mathrm {d} x}{\cos ax-\sin ax}}=-{\frac {x}{2}}-{\frac {1}{2a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|\sin ax-\cos ax\right|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\cos ax\;\mathrm {d} x}{\sin ax(1+\cos ax)}}=-{\frac {1}{4a}}\tan ^{2}{\frac {ax}{2}}+{\frac {1}{2a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|\tan {\frac {ax}{2}}\right|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\cos ax\;\mathrm {d} x}{\sin ax(1-\cos ax)}}=-{\frac {1}{4a}}\cot ^{2}{\frac {ax}{2}}-{\frac {1}{2a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|\tan {\frac {ax}{2}}\right|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\sin ax\;\mathrm {d} x}{\cos ax(1+\sin ax)}}={\frac {1}{4a}}\cot ^{2}\left({\frac {ax}{2}}+{\frac {\pi }{4}}\right)+{\frac {1}{2a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|\tan \left({\frac {ax}{2}}+{\frac {\pi }{4}}\right)\right|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\sin ax\;\mathrm {d} x}{\cos ax(1-\sin ax)}}={\frac {1}{4a}}\tan ^{2}\left({\frac {ax}{2}}+{\frac {\pi }{4}}\right)-{\frac {1}{2a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|\tan \left({\frac {ax}{2}}+{\frac {\pi }{4}}\right)\right|[fusion_builder_container hundred_percent=
{\displaystyle \int \sin ax\cos ax\;\mathrm {d} x=-{\frac {1}{2a}}\cos ^{2}ax+C\,\!}
{\displaystyle \int \sin a_{1}x\cos a_{2}x\;\mathrm {d} x=-{\frac {\cos((a_{1}-a_{2})x)}{2(a_{1}-a_{2})}}-{\frac {\cos((a_{1}+a_{2})x)}{2(a_{1}+a_{2})}}+C\qquad {\mbox{(for }}[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|a_{1}|\neq |a_{2}|[fusion_builder_container hundred_percent=
{\displaystyle \int \sin ^{n}ax\cos ax\;\mathrm {d} x={\frac {1}{a(n+1)}}\sin ^{n+1}ax+C\qquad {\mbox{(for }}n\neq -1{\mbox{)}}\,\!}
{\displaystyle \int \sin ax\cos ^{n}ax\;\mathrm {d} x=-{\frac {1}{a(n+1)}}\cos ^{n+1}ax+C\qquad {\mbox{(for }}n\neq -1{\mbox{)}}\,\!}
{\displaystyle \int \sin ^{n}ax\cos ^{m}ax\;\mathrm {d} x=-{\frac {\sin ^{n-1}ax\cos ^{m+1}ax}{a(n+m)}}+{\frac {n-1}{n+m}}\int \sin ^{n-2}ax\cos ^{m}ax\;\mathrm {d} x\qquad {\mbox{(for }}m,n>0{\mbox{)}}\,\!}
juga: {\displaystyle \int \sin ^{n}ax\cos ^{m}ax\;\mathrm {d} x={\frac {\sin ^{n+1}ax\cos ^{m-1}ax}{a(n+m)}}+{\frac {m-1}{n+m}}\int \sin ^{n}ax\cos ^{m-2}ax\;\mathrm {d} x\qquad {\mbox{(for }}m,n>0{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{\sin ax\cos ax}}={\frac {1}{a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\mathrm {d} x}{\sin ax\cos ^{n}ax}}={\frac {1}{a(n-1)\cos ^{n-1}ax}}+\int {\frac {\mathrm {d} x}{\sin ax\cos ^{n-2}ax}}\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\mathrm {d} x}{\sin ^{n}ax\cos ax}}=-{\frac {1}{a(n-1)\sin ^{n-1}ax}}+\int {\frac {\mathrm {d} x}{\sin ^{n-2}ax\cos ax}}\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\sin ax\;\mathrm {d} x}{\cos ^{n}ax}}={\frac {1}{a(n-1)\cos ^{n-1}ax}}+C\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\sin ^{2}ax\;\mathrm {d} x}{\cos ax}}=-{\frac {1}{a}}\sin ax+{\frac {1}{a}}\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\sin ^{2}ax\;\mathrm {d} x}{\cos ^{n}ax}}={\frac {\sin ax}{a(n-1)\cos ^{n-1}ax}}-{\frac {1}{n-1}}\int {\frac {\mathrm {d} x}{\cos ^{n-2}ax}}\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\sin ^{n}ax\;\mathrm {d} x}{\cos ax}}=-{\frac {\sin ^{n-1}ax}{a(n-1)}}+\int {\frac {\sin ^{n-2}ax\;\mathrm {d} x}{\cos ax}}\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\sin ^{n}ax\;\mathrm {d} x}{\cos ^{m}ax}}={\frac {\sin ^{n+1}ax}{a(m-1)\cos ^{m-1}ax}}-{\frac {n-m+2}{m-1}}\int {\frac {\sin ^{n}ax\;\mathrm {d} x}{\cos ^{m-2}ax}}\qquad {\mbox{(for }}m\neq 1{\mbox{)}}\,\!}
juga: {\displaystyle \int {\frac {\sin ^{n}ax\;\mathrm {d} x}{\cos ^{m}ax}}=-{\frac {\sin ^{n-1}ax}{a(n-m)\cos ^{m-1}ax}}+{\frac {n-1}{n-m}}\int {\frac {\sin ^{n-2}ax\;\mathrm {d} x}{\cos ^{m}ax}}\qquad {\mbox{(for }}m\neq n{\mbox{)}}\,\!}
juga: {\displaystyle \int {\frac {\sin ^{n}ax\;\mathrm {d} x}{\cos ^{m}ax}}={\frac {\sin ^{n-1}ax}{a(m-1)\cos ^{m-1}ax}}-{\frac {n-1}{m-1}}\int {\frac {\sin ^{n-2}ax\;\mathrm {d} x}{\cos ^{m-2}ax}}\qquad {\mbox{(for }}m\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\cos ax\;\mathrm {d} x}{\sin ^{n}ax}}=-{\frac {1}{a(n-1)\sin ^{n-1}ax}}+C\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}
{\displaystyle \int {\frac {\cos ^{2}ax\;\mathrm {d} x}{\sin ax}}={\frac {1}{a}}\left(\cos ax+\ln \left[/fusion_text][/fusion_builder_column][/fusion_builder_row][/fusion_builder_container]|\tan {\frac {ax}{2}}\right|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\cos ^{2}ax\;\mathrm {d} x}{\sin ^{n}ax}}=-{\frac {1}{n-1}}\left({\frac {\cos ax}{a\sin ^{n-1}ax)}}+\int {\frac {\mathrm {d} x}{\sin ^{n-2}ax}}\right)\qquad {\mbox{(for }}n\neq 1{\mbox{)}}}
{\displaystyle \int {\frac {\cos ^{n}ax\;\mathrm {d} x}{\sin ^{m}ax}}=-{\frac {\cos ^{n+1}ax}{a(m-1)\sin ^{m-1}ax}}-{\frac {n-m+2}{m-1}}\int {\frac {\cos ^{n}ax\;\mathrm {d} x}{\sin ^{m-2}ax}}\qquad {\mbox{(for }}m\neq 1{\mbox{)}}\,\!}
juga: {\displaystyle \int {\frac {\cos ^{n}ax\;\mathrm {d} x}{\sin ^{m}ax}}={\frac {\cos ^{n-1}ax}{a(n-m)\sin ^{m-1}ax}}+{\frac {n-1}{n-m}}\int {\frac {\cos ^{n-2}ax\;\mathrm {d} x}{\sin ^{m}ax}}\qquad {\mbox{(for }}m\neq n{\mbox{)}}\,\!}
juga: {\displaystyle \int {\frac {\cos ^{n}ax\;\mathrm {d} x}{\sin ^{m}ax}}=-{\frac {\cos ^{n-1}ax}{a(m-1)\sin ^{m-1}ax}}-{\frac {n-1}{m-1}}\int {\frac {\cos ^{n-2}ax\;\mathrm {d} x}{\sin ^{m-2}ax}}\qquad {\mbox{(for }}m\neq 1{\mbox{)}}\,\!}

Integral trigonometri – Integrand melibatkan baik sinus dan tangen

{\displaystyle \int \sin ax\tan ax\;\mathrm {d} x={\frac {1}{a}}(\ln[/fusion_text][/fusion_builder_column] [/fusion_builder_row][/fusion_builder_container]|[fusion_builder_container hundred_percent=
{\displaystyle \int {\frac {\tan ^{n}ax\;\mathrm {d} x}{\sin ^{2}ax}}={\frac {1}{a(n-1)}}\tan ^{n-1}(ax)+C\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}

Integral trigonometri – Integrand melibatkan baik kosinus dan tangen

{\displaystyle \int {\frac {\tan ^{n}ax\;\mathrm {d} x}{\cos ^{2}ax}}={\frac {1}{a(n+1)}}\tan ^{n+1}ax+C\qquad {\mbox{(for }}n\neq -1{\mbox{)}}\,\!}

Integral trigonometri – Integrand melibatkan baik sinus dan kotangen

{\displaystyle \int {\frac {\cot ^{n}ax\;\mathrm {d} x}{\sin ^{2}ax}}=-{\frac {1}{a(n+1)}}\cot ^{n+1}ax+C\qquad {\mbox{(for }}n\neq -1{\mbox{)}}\,\!}

Integral trigonometri – Integrand melibatkan baik kosinus dan kotangen

{\displaystyle \int {\frac {\cot ^{n}ax\;\mathrm {d} x}{\cos ^{2}ax}}={\frac {1}{a(1-n)}}\tan ^{1-n}ax+C\qquad {\mbox{(for }}n\neq 1{\mbox{)}}\,\!}

Integral trigonometri – Integrand melibatkan baik sekan dan tangen

{\displaystyle \int \sec x\tan x\;\mathrm {d} x=\sec x+C}

Integral dengan limit simetris

{\displaystyle \int _{-c}^{c}\sin {x}\;\mathrm {d} x=0\!}
{\displaystyle \int _{-c}^{c}\cos {x}\;\mathrm {d} x=2\int _{0}^{c}\cos {x}\;\mathrm {d} x=2\int _{-c}^{0}\cos {x}\;\mathrm {d} x=2\sin {c}\!}
{\displaystyle \int _{-c}^{c}\tan {x}\;\mathrm {d} x=0\!}
{\displaystyle \int _{-{\frac {a}{2}}}^{\frac {a}{2}}x^{2}\cos ^{2}{\frac {n\pi x}{a}}\;\mathrm {d} x={\frac {a^{3}(n^{2}\pi ^{2}-6)}{24n^{2}\pi ^{2}}}\qquad {\mbox{(for }}n=1,3,5...{\mbox{)}}\,\!}
{\displaystyle \int _{\frac {-a}{2}}^{\frac {a}{2}}x^{2}\sin ^{2}{\frac {n\pi x}{a}}\;\mathrm {d} x={\frac {a^{3}(n^{2}\pi ^{2}-6(-1)^{n})}{24n^{2}\pi ^{2}}}={\frac {a^{3}}{24}}(1-6{\frac {(-1)^{n}}{n^{2}\pi ^{2}}})\qquad {\mbox{(for }}n=1,2,3,...{\mbox{)}}\,\!}

Integral satu lingkaran penuh

{\displaystyle \int _{0}^{2\pi }\sin ^{2m+1}{x}\cos ^{2n+1}{x}\;\mathrm {d} x=0\!\qquad \{n,m\}\in \mathbb {Z} }

Fungsi trigonometrik

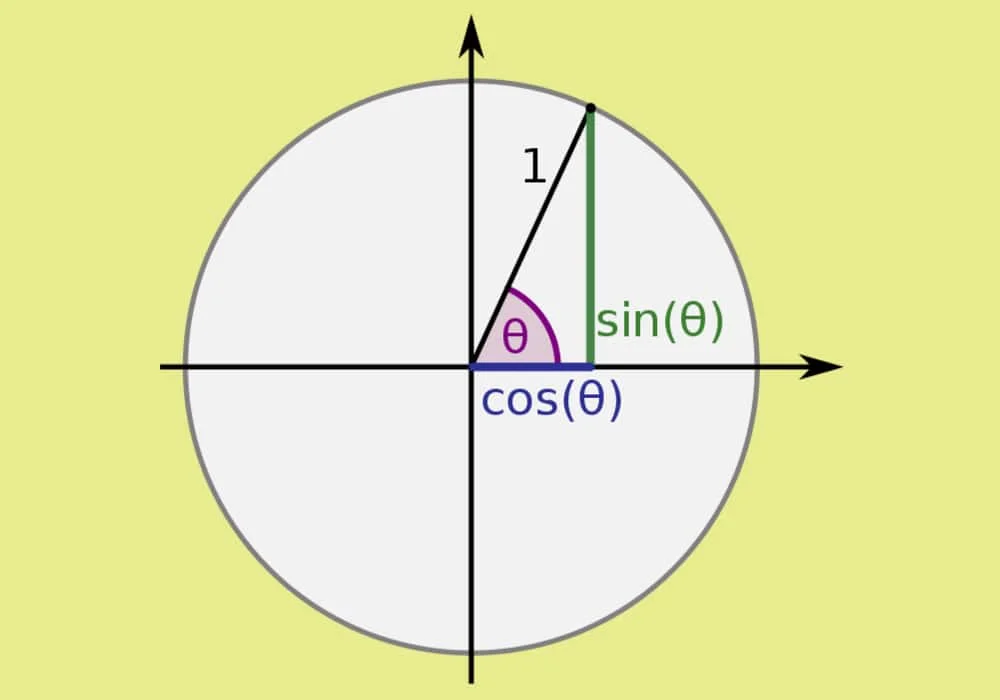
Fungsi trigonometrik adalah fungsi dari sebuah sudut yang digunakan untuk menghubungkan antara sudut-sudut dalam suatu segitiga dengan sisi-sisi segitiga tersebut.

Rtriangle.svg

Fungsi trigonometrik diringkas di tabel di bawah ini. Sudut theta  adalah sudut yang diapit oleh sisi miring dan sisi samping—sudut A pada gambar di samping, a adalah sisi depan, b adalah sisi samping, dan c adalah sisi miring:

FungsiSingkatanDeskripsiIdentitas (memggunakan radian)
Sinussin
Kosinuscos
Tangentan (atau tg)
Kotangencot (atau ctg atau ctn)
Sekansec
Kosekancsc (atau cosec)

Contoh Soal dan Jawaban Integral trigonometri

1. Soal: Tentukan hasil dari ∫sin4 x dx =…

Jawaban:

∫sin4 x dx
=∫ (sin2 x)2 dx
= ∫ (1/2 – 1/2 cos 2x)2 dx
= ∫ (1/4 – 1/2 cos 2x + 1/4 cos2 2x) dx
= ∫ (1/4 – 1/2 cos 2x + 1/4 (1/2 + 1/2 cos 4x)) dx
= ∫ (1/4 – 1/2 cos 2x + 1/8 + 1/8 cos 4x) dx
= ∫ (3/8 – 1/2 cos 2x + 1/8 cos 4x) dx
= 3/8 x – 1/4 sin 2x + 1/32 sin 4x + c

2. Soal: ∫ (x2 – 4x) cos (x3 – 6x2 + 7) dx =…

Jawaban:

misal y = x3 – 6x2 + 7
maka dy/dx = 3x2 – 12x
sehingga dx = dy/(3x2 – 12x)
atau  dx = 1/3 dy/(x2 – 4x)

Jadi

∫ (x2 – 4x) cos (x3 – 6x2 + 7) dx
= ∫ (x2 – 4x) cos y 1/3 dy/(x2 – 4x)
= 1/3 ∫ cos y dy
= 1/3 sin y + c
= 1/3 sin (x3 – 6x2 + 7) + c

3. Soal:  \int sin^2\;3x\; dx = …..

Jawaban:

Gunakan rumus trigonometri
{\color{Red} sin^2\;x=\frac 12-\frac 12\;cos\;2x}   sehingga
 \begin{align*}sin^2\;3x&=&\frac 12-\frac 12\;cos\;2(3x)\\&=&\frac 12-\frac 12\;cos\;6x \end{align*}
Maka :
\begin{align*}\int sin^2\;3x\;dx&=&\int \left (\frac 12-\frac 12\;cos\;6x \right )dx\\&=&\frac 12x-\frac 12.\frac 16\;sin\;6x+C\\&=&\frac 12x-\frac{1}{12}\;sin\;6x+C \end{align*}

4. Soal: ∫ cos4 x dx

Jawaban:

∫ cos4 x dx
=∫ (cos2 x)2 dx
= ∫ (1/2 + 1/2 cos 2x)2 dx
= ∫ (1/4 + 1/2 cos 2x + 1/4 cos2 2x) dx
= ∫ (1/4 + 1/2 cos 2x + 1/4 (1/2 + 1/2 cos 4x)) dx
= ∫ (1/4 + 1/2 cos 2x + 1/8 + 1/8 cos 4x) dx
= ∫ (3/8 + 1/2 cos 2x + 1/8 cos 4x) dx
= 3/8 x + 1/4 sin 2x + 1/32 sin 4x + c

5. Soal: ∫ (tan 2x − sec 2x)2 dx =…

Jawaban:
⇒ ∫ (tan22x + sec22x − 2 sec 2x tan 2x) dx
⇒ ∫ (sec22x − 1 + sec22x − 2 sec 2x tan 2x) dx
⇒ ∫ (2sec22x − 2 sec 2x tan 2x − 1) dx
= 2/2tan 2x − 2/2sec 2x − x + C
= tan 2x − sec 2x − x + C

6. Soal: ∫ (tan24x + 3) dx =…

Jawaban:
⇒ ∫ (sec24x − 1 + 3) dx
⇒ ∫ (sec24x + 2) dx
= ¼tan 4x + 2x + C

7. Soal: \displaystyle \int \sqrt{1+\sin 2x} \, \mathrm{d}x = ...

Jawaban:

Karena   \cos^2x+\sin^2x = 1    dan   \sin 2x = 2 \sin x \cos x   sehingga

\displaystyle \begin{aligned} \int \sqrt{1 + \sin 2x} &= \int \sqrt{\cos^2 x + \sin 2x + \sin^2 x} \, \mathrm{d}x \\ & = \int \sqrt{\cos^2x + 2\sin x \cos x+ \sin^2x} \, \mathrm{d}x \\ & = \int \sqrt{(\cos x + \sin x)^2} \, \mathrm{d}x \\ & = \int (\cos x + \sin x) \, \mathrm{d}x \\ & = \sin x - \cos x + C \end{aligned}

Jawaban : \sin x - \cos x + C

8. Soal: \displaystyle \int \left( \sin x + \sin^3 x + \sin^5 + \dots \right) \, \mathrm{d}x = ...

Jawaban:

Bentuk dalam integral merupakan Deret Geometri tak hingga dengan suku pertama a = \sin xdan rasio r = \sin^2 x, sehingga bentuk integral tersebut dapat ditulis

\displaystyle \begin{aligned} \int \left( \sin x + \sin^3 x + \sin^5 + \dots \right) \, \mathrm{d}x &= \int \dfrac{\sin x}{1-\sin^2 x} \, \mathrm{d}x \end{aligned}

Dengan memisalkan u = \cos x \rightarrow -\mathrm{d}u = \sin x \, \mathrm{d}x dan mengganti 1 - \sin^2 x = \cos^2 x = u^2 maka

\displaystyle \begin{aligned} \int \dfrac{\sin x}{1-\sin^2 x} \, \mathrm{d}x &= \int \dfrac{1}{u^2} \, (-\mathrm{d}u) \\ &= u^{-1} + C \\ &= \sec x + C \\ \end{aligned}

9. Soal: \displaystyle \int \sqrt{1-\cos x} \, \mathrm{d}x = ...

Jawaban:

Dari persamaan trigonometri \cos x = 1 - 2\sin^2\frac{1}{2}x

\displaystyle \begin{aligned} \int \sqrt{1-\cos x} \, \mathrm{d}x &= \int \sqrt{1-(1-2\sin ^2 \frac{1}{2}x)} \, \mathrm{d}x \\ &= \int \sqrt{2\sin^2\frac{1}{2}x} \, \mathrm{d}x \\ &= \sqrt{2} \int \sin \frac{1}{2}x \, \mathrm{d}x \\ &= -2\sqrt{2} \cos \frac{1}{2}x + C \end{aligned}

Jawaban : -2\sqrt{2} \cos \frac{1}{2}x + C

10. Soal: 

∫ (x + 3) cos (2x − π)dx =…..
|____| |__________|
u                  dv

Jawaban:

Langkah pertama yaitu tentukan terlebih dulu mana u dan mana dv
Misalkan

(x + 3) adalah u, dan sisanya, cos (2x − π)dx sebagai dv,
u = (x + 3) …(Persamaan 1)
dv = cos (2x − π) dx … (Persamaan 2)

Langkah pertama selesai, kita tengok lagi rumus dasar integral parsial:

∫ u dv = uv − ∫v du

Terlihat di situ kita perlu u, perlu v dan perlu du. u nya sudah ada, tinggal mencari du dan v nya.

Dari persamaan 1, untuk menentukan du, caranya turunkan u nya,
u = (x + 3)
du/dx = 1
du = dx

Dari persamaan 2, untuk menentukan v,
dv = cos (2x − π)dx
atau
dv/dx = cos (2x − π)

dv/dx artinya turunan dari v adalah cos (2x − π), untuk mendapatkan v, berarti kita harus integralkan cos (2x − π) jika lupa, tengok lagi cara integral fungsi trigonometri,

v = ∫ cos (2x − π) dx = 1/2 sin (2x − π) + C

Kita rangkum lagi :
u = (x + 3)
v = 1/2 sin (2x − π)
du = dx

masukkan nilai-nilai yang sudah dicari tadi sesuai rumus integral parsial:
16 ∫ (x + 3) cos (2x − π)dx
Simpan dulu 16 nya, terakhir nanti hasilnya baru di kali 16
= uv − ∫v du
= (x + 3) 1/2 sin (2x − π) − ∫ 1/2 sin (2x − π) du
= 1/2 (x + 3) sin (2x − π) − ∫ 1/2 sin (2x − π) dx
= 1/2 (x + 3) sin (2x − π) − 1/2 {− 1/2 cos (2x − π) }
= 1/2 (x + 3) sin (2x − π) + 1/4 cos (2x − π)

kalikan 16, tambahkan + C nya

= 16 { 1/2 (x + 3) sin (2x − π) + 1/4 cos (2x − π) } + C
= 8 (x + 3) sin (2x − π) + 4 cos (2x − π) + C

11. Soal:   \[ \int cos \left( 2x + 5 \right) \; dx = ...\]

Pembahasan:
Misalkan:

  \[ u = 2x + 5 \]

  \[ du = 2 dx \rightarrow dx = \frac{du}{2} \]

Sehingga,

  \[ \int cos \left( 2x + 5 \right) \; dx = \int cos \; u \; \frac{du}{2} \]

  \[ = \frac{1}{2} \int cos \; u \; du \]

  \[ = \frac{1}{2} sin \; u + C \]

  \[ = \frac{1}{2} sin \; \left(2x + 5 \right) + C \]

Bacaan Lainnya Yang Dapat Membuat Anda lebih Pintar

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ohh begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: Mathworks

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing

Pinter Pandai
«
»

Nilai Pi 1 juta digit pertama | Analisis dan…

PinterPandai
Mei 8, 2024 1 min read

Menghitung Dimensi Balok dari Luas Jaring-Jaringnya

Pinter Pandai
Apr 27, 2024 1 min read

Rumus Matematika dan Contoh untuk Penggunaan Sehari-hari

PinterPandai
Jul 17, 2023 6 min read

2 Replies to “Integral Trigonometri – Fungsi Beserta Contoh Soal dan Jawaban”

Tinggalkan Balasan

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *