Kecepatan suara
Kecepatan suara adalah istilah yang digunakan untuk menyebut kecepatan gelombang suara yang merambat pada medium elastisitas.
Pada ketinggian air laut, dengan suhu 20 °C (68 °F) dan kondisi atmosfer normal, kecepatan suara adalah 343 m/detik (1238 km/jam). Kecepatan rambatan gelombang suara ini dapat berbeda tergantung medium yang dilewati (misalnya suara lebih cepat melalui air daripada udara), sifat-sifat medium tersebut dan suhu.
Kecepatan suara pada gas ideal hanya tergantung pada suhu dan komposisinya. Kecepatan memiliki ketergantungan lemah terhadap frekuensi dan tekanan pada udara normal, berbeda sedikit dari keadaan ideal.
Kecepatan suara adalah istilah yang digunakan untuk menggambarkan kecepatan gelombang suara yang melewati medium elastis.
Dalam pembahasan sehari-hari, kecepatan suara mengacu kepada kecepatan gelombang suara pada udara. Namun, besar kecepatan suara berbeda dari substansi ke substansi: paling lambat dalam gas; lebih cepat dalam cairan; lebih cepat lagi dalam benda padat. Misalnya, di udara adalah 343 m/detik; di air 1.484 m/detik (4,3 kali); dan di besi 5.120 m/s. Pada beberapa benda yang sangat keras seperti berlian, suara merambat dengan kecepatan 12.000 m/detik; yang merupakan kecepatan maksimum suara pada kondisi normal.
Gelombang suara dalam benda padat terdiri dari gelombang-gelombang kompresi, dan sebuah tipe gelombang suara yang disebut gelombang geser, yang hanya muncul pada benda padat. Gelombang geser dalam benda padat biasanya merambat pada kecepatan berbeda-beda, seperti ditunjukkan dalam seismologi. Kecepatan gelombang kompresi dalam benda padat ditentukan oleh kompresibilitas, modulus geser, dan densitas medium. Kecepatan gelombang geser ditentukan hanya dari modulus geser dan densitas material padat.
Dalam dinamika fluida, kecepatan suara pada medium cair (gas atau liquid) digunakan sebagai pengukuran relatif untuk kecepatan objek yang bergerak melalui medium tersebut. Rasio antara kecepatan objek terhadap kecepatan suara dalam fluida disebut bilangan Mach. Objek yang bergerak melebihi Mach1 disebut bergerak dengan kecepatan supersonik.
Persamaan Kecepatan Suara
Kecepatan suara dalam notasi matematika dilambangkan dengan c, dari bahasa Latin celeritas yang berarti “kelajuan”.
Secara umum, kecepatan suara c dinyatakan dengan persamaan Newton–Laplace:
dengan
- Ks adalah koefisien kekerasan, modulus bulk isentropik (atau modulus elastisitas bulk untuk gas);
- ρ adalah massa jenis.
Maka kecepatan suara meningkat berbanding lurus dengan kekerasan material (resistansi benda elastis terhadap deformasi akibat gaya yang bekerja pada benda tersebut) dan berbanding terbalik dengan meningkatnya massa jenis. Untuk gas ideal, modulus bulk K sederhananya adalah tekanan gas dikali indeks adiabatik, yang nilainya 1,4 untuk udara dibawah kondisi tekanan dan temperatur normal.
Untuk persamaan keadaan umum, jika digunakan mekanika klasik, kecepatan suara c dinyatakan dengan
dengan
- p adalah tekanan;
- ρ adalah massa jenis dan turunan diambil secara isentropis, maka pada entropi konstan s.
Jika efek relativistik menjadi penting, maka kecepatan suara dihitung dari persamaan Euler relativistik.
Dalam medium non-dispersif, kecepatan suara tidak tergantung frekuensi bunyi, maka kecepatan transportasi energi dan perambatan bunyi sama untuk semua frekuensi. Udara, campuran oksigen dan nitrogen, membentuk medium non non-dispersif. Namun, udara juga mengandung sebagian kecil CO2, yang merupakan medium dispersif, dan menyebabkan dispersi ke udara pada frekuensi ultrasonik (> 28 kHz).
Dalam medium dispersif, kecepatan suara merupakan fungsi frekuensi bunyi, melalui hubungan dispersi. Tiap komponen frekuensi merambat pada kecepatannya masing-masing, disebut kelajuan fasa, sedangkan energi disturbansi merambat pada kelajuan grup. Fenomena yang sama muncul dengan gelombang cahaya; lihat dispersi optik untuk penjelasan.
Rumus Kecepatan Suara Untuk Udara Kering
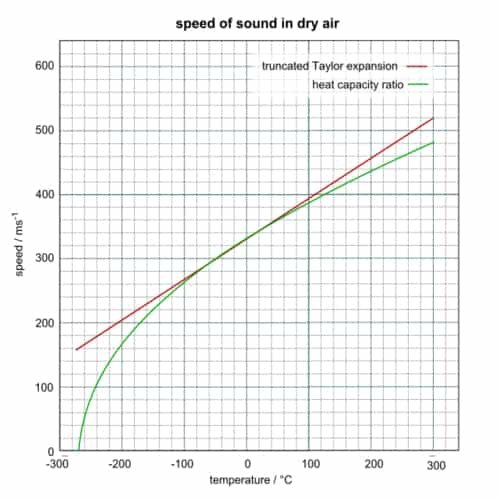
Perkiraan kecepatan suara dalam keadaan udara kering (kelembaban 0%), dalam meter per sekon, suhu mendekati 0 °C, dapat dihitung dari
dimana 
Persamaan ini diturunkan dari 2 term pertama ekspansi Taylor dari persamaan berikut:
Nilai 331.3 m/s, yang menghasilkan kecepatan pada 0 °C (atau 273.15 K), didasarkan pada nilai teoretis rasio kapasitas panas, γ, juga fakta bahwa pada tekanan udara 1 atm sangat bisa dijelaskan oleh perkiraan gas ideal. Beberapa nilai kecepatan suara pada 0 °C dapat bervariasi mulai 331.2 sampai 331.6 karena asumsia-asumsi ketika penghitungan. Jika gas ideal γ diasumsikan tepat 7/5 = 1.4, maka kecepatan suara pada 0 °C akan menghasilkan angka 331.3 m/s.
Persamaan ini dapat digunakan untuk rentang temperatur yang lebar, namun tetap bergantung pada perkiraan rasio kapasitas panas, dan untuk alasan ini tidak dapat digunakan pada suhu yang sangat tinggi. Rumus ini akan menghasilkan prediksi yang baik pada kondisi relatif kering, dingin, tekanan rendah, seperti stratofer bumi. Persamaan ini tidak dapat digunakan untuk tekanan sangat rendah dan panjang gelombang pendek, karena ketergantungan pada asumsi bahwa panjang gelombang suara dalam gas jauh lebih panjang daripada jarak bebas rata-rata antara tumbukan molekul gas.

Efek Karena Gesekan Angin / Pengaruh Suhu Pada Sifat Udara
Kecepatan suara bervariasi dengan suhu. Karena suhu dan kecepatan suara biasanya menurun dengan meningkatnya ketinggian, suara dibiaskan ke atas, menjauh dari pendengar di tanah, menciptakan bayangan akustik pada jarak tertentu dari sumbernya. Gesekan angin sebesar 4 m / (s · km) dapat menghasilkan pembiasan sama dengan tingkat suhu tunda standar sebesar 7,5 ° C / km.
Nilai lebih tinggi dari gradien angin akan membiaskan suara ke bawah menuju permukaan dalam arah melawan arah angin, menghilangkan bayangan akustik pada sisi melawan arah angin. Ini akan meningkatkan kemampuan mendengar suara melawan arah angin. Efek pembiasan arah angin bawah ini terjadi karena ada gradien angin; suara tidak dibawa oleh angin.
Untuk propagasi suara, variasi kecepatan angin eksponensial dengan tinggi dapat didefinisikan sebagai berikut:
yang dimana:
- U (h) adalah kecepatan angin pada ketinggian h;
- ζ adalah koefisien eksponensial berdasarkan kekasaran permukaan tanah, biasanya antara 0,08 dan 0,52;
- dU / dH (h) adalah gradien angin yang diharapkan pada ketinggian h.
Pada 1862 Perang Saudara Amerika Iuka, bayangan akustik, yang diyakini telah ditingkatkan oleh angin timur laut, membuat dua divisi pasukan Union keluar dari pertempuran, karena mereka tidak dapat mendengar suara pertempuran hanya 10 km (enam mil) ) melawan arah angin.
Dalam atmosfer standar:
- T0 adalah 273.15 K (= 0 °C = 32 °F), memberikan nilai teoritis 331.3 m/s (= 1086.9 ft/s = 1193 km/h = 741.1 mph = 644.0 kn). Nilai mulai dari 331.3 to 331.6 m/s dapat ditemukan dalam literatur referensi, namun;
- T20 is 293.15 K (= 20 °C = 68 °F), memberikan nilai 343.2 m/s (= 1126.0 ft/s = 1236 km/h = 767.8 mph = 667.2 kn);
- T25 is 298.15 K (= 25 °C = 77 °F), memberikan nilai 346.1 m/s (= 1135.6 ft/s = 1246 km/h = 774.3 mph = 672.8 kn).
Bahkan, dengan asumsi gas yang ideal, kecepatan suara c hanya bergantung pada suhu, bukan tekanan atau kerapatan (karena perubahan ini berbatasan dengan suhu tertentu dan membatalkan). Udara hampir merupakan gas ideal. Suhu udara bervariasi dengan ketinggian, memberikan variasi kecepatan suara berikut menggunakan atmosfer standar — kondisi sebenarnya dapat bervariasi.
Pengaruh suhu pada sifat udara
| Suhu T (°C) | Kecepatan suara c (m/s) | Densitas udara ρ (kg/m3) | Karakteristik impedansi akustik tertentu z0 (Pa·s/m) |
|---|---|---|---|
| 35 | 351.88 | 1.1455 | 403.2 |
| 30 | 349.02 | 1.1644 | 406.5 |
| 25 | 346.13 | 1.1839 | 409.4 |
| 20 | 343.21 | 1.2041 | 413.3 |
| 15 | 340.27 | 1.2250 | 416.9 |
| 10 | 337.31 | 1.2466 | 420.5 |
| 5 | 334.32 | 1.2690 | 424.3 |
| 0 | 331.30 | 1.2922 | 428.0 |
| −5 | 328.25 | 1.3163 | 432.1 |
| −10 | 325.18 | 1.3413 | 436.1 |
| −15 | 322.07 | 1.3673 | 440.3 |
| −20 | 318.94 | 1.3943 | 444.6 |
| −25 | 315.77 | 1.4224 | 449.1 |
Dengan kondisi atmosfer normal, suhu, dan dengan demikian kecepatan suara, bervariasi dengan ketinggian
| Ketinggian | Temperature | m/s | km/h | mph | kn |
| Permukaan laut | 15 °C (59 °F) | 340 | 1,225 | 761 | 661 |
| 11,000 m−20,000 m (Menjelajahi ketinggian jet komersial, dan penerbangan supersonik pertama) | −57 °C (−70 °F) | 295 | 1,062 | 660 | 573 |
| 29,000 m (Penerbangan Boeing X-43A) | −48 °C (−53 °F) | 301 | 1,083 | 673 | 585 |
Kecepatan Suara Pada Material Lain
Material | Kecepatan Suara |
Karet | 60 m/s |
Udara pada 40oC | 355 m/s |
Udara pada 20 oC | 343 m/s |
Timah | 1210 m/s |
Emas | 3240 m/s |
Kaca | 4540 m/s |
Tembaga | 4600 m/s |
Aluminum | 6320 m/s |
Apa yang terjadi ketika ada perubahan dalam materi yang dilalui oleh suara?
Kecepatan suara tidak selalu sama. Ingat bahwa suara adalah getaran energi kinetik yang dilewatkan dari molekul ke molekul. Semakin dekat molekul satu sama lain dan semakin erat ikatannya, semakin sedikit waktu yang diperlukan bagi mereka untuk melewatkan suara satu sama lain dan suara yang lebih cepat dapat melakukan perjalanan.
Lebih mudah bagi gelombang bunyi untuk melewati zat padat daripada melalui cairan karena molekul-molekul lebih dekat dan lebih terikat erat dalam padatan. Demikian pula, lebih sulit bagi suara untuk melewati gas daripada melalui cairan, karena molekul gas lebih jauh terpisah. Kecepatan suara lebih cepat dalam material padat dan lebih lambat dalam cairan atau gas. Kecepatan gelombang suara dipengaruhi oleh dua sifat materi: sifat elastis dan densitas. Hubungan ini dijelaskan oleh persamaan berikut.

Yang dimana: Cij adalah sifat elastis dan p adalah densitas.
Suhu dan Kecepatan Suara
Suhu juga merupakan kondisi yang mempengaruhi kecepatan suara. Panas, seperti suara, adalah bentuk energi kinetik. Molekul pada suhu yang lebih tinggi memiliki lebih banyak energi, sehingga mereka dapat bergetar lebih cepat. Karena molekul bergetar lebih cepat, gelombang suara dapat melakukan perjalanan lebih cepat. Kecepatan suara di udara suhu kamar adalah 346 meter per detik. Ini lebih cepat dari 331 meter per detik, yang merupakan kecepatan suara di udara pada suhu beku.
Rumus untuk menemukan kecepatan suara di udara adalah sebagai berikut:
v = 331m / s + 0.6m / s / C * T
v adalah kecepatan suara dan T adalah suhu udara. Satu hal yang perlu diingat adalah bahwa rumus ini menemukan kecepatan rata-rata suara untuk suhu tertentu. Kecepatan suara juga dipengaruhi oleh faktor lain seperti kelembaban dan tekanan udara.
Contoh Soal Kecepatan Suara / Cepat Rambat Gelombang Bunyi
Tentukan frekuensi dan periode gelombang bunyi jika panjang gelombang 10 meter dan cepat rambat bunyi 350 m/s!
Pembahasan:
Diketahui: v = 350 m/s
λ = 10 meter
Ditanya: (A). frekuensi (f) dan (B). Peridoe (T)
Jawaban: a. v = λ x f
f = v / λ
f = 350/10 = 35 Hz
- v = λ / T
T = λ / v
T = 10/350 = 1/35 sekon
(Jika ingin menggunakan rumus cepat, ingat : T=1f=135 sekon)
Sebuah kapal mengukur kedalaman laut menggunakan perangkat suara. Jika bunyi ditembakkan ke dasar laut, bunyi pantul diterima setelah 10 detik. Tentukan kedalaman laut tersebut jika cepat rambat bunyi 1600 m/s!
Pembahasan:
Diketahui: t = 10 s
v = 1600 m/s
Ditanya: s ?
Jawaban: S= vt/2 (panjang gelombang harus dibagi 2, karena akan memantul dan kembali lagi ke kapal)
S = (1600 x 10) / 2 = 8000 m
Bacaan Lainnya
- Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang
- Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender
- Cara Menghentikan Penindasan Bullying
- Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
- Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
- 10 Cara Memotivasi Anak Untuk Belajar Agar Menjadi Pintar
- Di Indonesia, (HAN) Hari Anak Nasional tanggal 23 Juli
- Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
- Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Live Science, NASA, NDT Resource Center
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya






