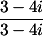Bilangan Kompleks

Bilangan kompleks adalah gabungan antara bilangan Real dengan bilangan Imajiner.

Dalam pelajaran matematika, bilangan ini adalah bilangan yang berbentuk

a+bi

di mana a dan b adalah bilangan riil, dan i adalah bilangan imajiner tertentu yang mempunyai sifat i² = −1. Bilangan riil a disebut juga bagian riil dari bilangan kompleks dan bilangan real b disebut bagian imajiner.

Jika pada suatu bilangan kompleks, nilai b adalah 0, maka bilangan kompleks tersebut menjadi sama dengan bilangan real a.

Sebagai contoh, 3 + 2i adalah bilangan kompleks dengan bagian riil 3 dan bagian imajiner 2i.

Bilangan ini dapat ditambah, dikurang, dikali dan dibagi seperti bilangan riil; namun bilangan ini juga mempunyai sifat-sifat tambahan yang menarik.

Misalnya, setiap persamaan aljabar polinomial (suku banyak) mempunyai solusi bilangan kompleks, tidak seperti bilangan riil yang hanya memiliki sebagian.

Dalam bidang-bidang tertentu (seperti teknik elektro, di mana i digunakan sebagai simbol untuk arus listrik), bilangannya ditulis a + bj.

Penjelasan bilangan kompleks

Dalam matematika, himpunan bilangan kompleks dibuat sebagai perpanjangan dari himpunan bilangan real, yang mengandung khususnya bilangan imajiner yang dicatat ia, b sehingga i2 = −1. Kuadrat dari (−i) juga sama dengan −1: (−i) 2 = −1.

Bilangan kompleks apa pun dapat ditulis sebagai a + i b di mana a dan b adalah bilangan real.

Kita dapat menyediakan himpunan bilangan kompleks dengan penjumlahan dan perkalian yang membuatnya menjadi bidang komutatif yang berisi bidang bilangan real. Ini disebut bidang bilangan kompleks dan ditulis ℂ.

Pengertian nilai absolut yang didefinisikan pada himpunan bilangan real dapat diperluas ke himpunan bilangan kompleks dan kemudian mengambil nama modul.

Tetapi kita tidak dapat menyediakan himpunan bilangan kompleks dengan relasi urutan yang akan membuatnya menjadi bidang yang terurut secara total, artinya tidak mungkin membandingkan dua kompleks sambil menghormati aturan prosedur operasi yang berlaku untuk bilangan real.

Bentuk Penjumlahan

Pada umumnya dinyatakan sebagai penjumlahan 2 suku, dengan suku pertama adalah bilangan riil dan suku kedua adalah bilangan imajiner.

a+bi

Angka kompleks ditambahkan dengan menambahkan secara terpisah bagian nyata dan imajiner dari summands. Artinya:

Bentuk Penjumlahan

(a+bi) + (c+di) = (a+c) + (b+d)i

Bentuk Pengurangan

(a+bi) – (c+di) = (a-c) + (b-d)i

Bentuk Perkalian

Perkalian dalam dua bilangan kompleks dengan rumus berikut:

(a+bi) (c+di) = (ac-bd) + (bc+ad)i

Secara khusus, kuadrat i adalah -1:

i² = i x i = -1

Definisi sebelumnya tentang penggandaan bilangan kompleks secara umum mengikuti secara alami dari properti fundamental i. Memang, jika saya diperlakukan sebagai angka sehingga berarti d kali i, aturan perkalian di atas identik dengan peraturan biasa untuk mengalikan dua jumlah dari dua syarat.

Bentuk Pembagian

Pembagian dua bilangan kompleks didefinisikan dalam hal perkalian kompleks, yang dijelaskan di atas, dan pembagian nyata. Bila setidaknya satu dari c dan d tidak nol, jadi:

${\frac {a+bi}{c+di}}=\left({ac+bd \over c^{2}+d^{2}}\right)+\left({bc-ad \over c^{2}+d^{2}}\right)i.$

Pembagian dapat didefinisikan dengan cara ini, karena pengamatan sebagai berikut:

${\frac {a+bi}{c+di}}={\frac {\left(a+bi\right)\cdot \left(c-di\right)}{\left(c+di\right)\cdot \left(c-di\right)}}=\left({ac+bd \over c^{2}+d^{2}}\right)+\left({bc-ad \over c^{2}+d^{2}}\right)i.$

Bentuk Polar

Dengan menganggap bahwa:

r={\sqrt {a^{2}+b^{2}}}

dan

\theta =\arctan \left({\frac {b}{a}}\right)

maka

a+bi=r(\cos \theta +i\sin \theta )

Untuk mempersingkat penulisan, bentuk $r(\cos \theta +i\sin \theta )$ juga sering ditulis sebagai $r\,cis\theta$ .

Bentuk Eksponen

Bentuk lain adalah bentuk eksponen, yaitu:

re^{i\theta }=r(\cos \theta +i\sin \theta )

Bidang kompleks

Bilangan kompleks dapat divisualisasikan sebagai titik atau vektor posisi pada sistem koordinat dua dimensi yang dinamakan bidang kompleks atau Diagram Argand.

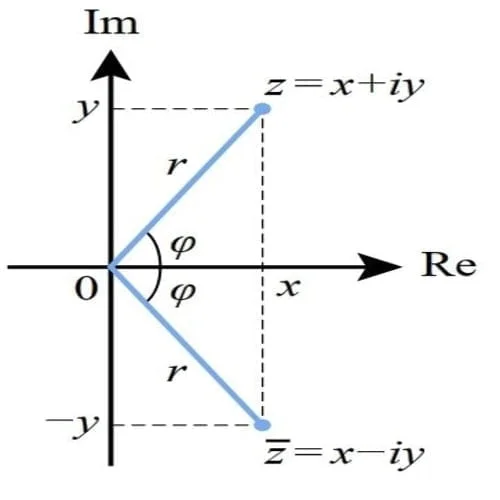
Koordinat Kartesius bilangan kompleks adalah bagian riil x dan bagian imajiner y, sedangkan koordinat sirkulernya adalah r = |z|, yang disebut modulus, dan φ = arg(z), yang disebut juga argumen kompleks dari z (Format ini disebut format mod-arg). Dikombinasikan dengan Rumus Euler, dapat diperoleh:

z=x+iy=r(\cos \phi +i\sin \phi )=re^{i\phi }.\,

Kadang-kadang, notasi r cis φ dapat juga ditemui.

Perlu diperhatikan bahwa argumen kompleks adalah unik modulo 2π, jadi, jika terdapat dua nilai argumen kompleks yang berbeda sebanyak kelipatan bilangan bulat dari 2π, kedua argumen kompleks tersebut adalah sama (ekivalen).

Dengan menggunakan identitas trigonometri dasar, dapat diperoleh:

r_{1}e^{i\phi _{1}}\cdot r_{2}e^{i\phi _{2}}=r_{1}r_{2}e^{i(\phi _{1}+\phi _{2})}\,

dan

{\frac {r_{1}e^{i\phi _{1}}}{r_{2}e^{i\phi _{2}}}}={\frac {r_{1}}{r_{2}}}e^{i(\phi _{1}-\phi _{2})}.\,

Penjumlahan dua bilangan kompleks sama seperti penjumlahan vektor dari dua vektor, dan perkalian dengan bilangan kompleks dapat divisualisasikan sebagai rotasi dan pemanjangan secara bersamaan.

Perkalian dengan i adalah rotasi 90 derajat berlawanan dengan arah jarum jam $\pi /2$ radian). Secara geometris, persamaan i² = −1 adalah dua kali rotasi 90 derajat yang sama dengan rotasi 180 derajat ( $\pi$ radian).

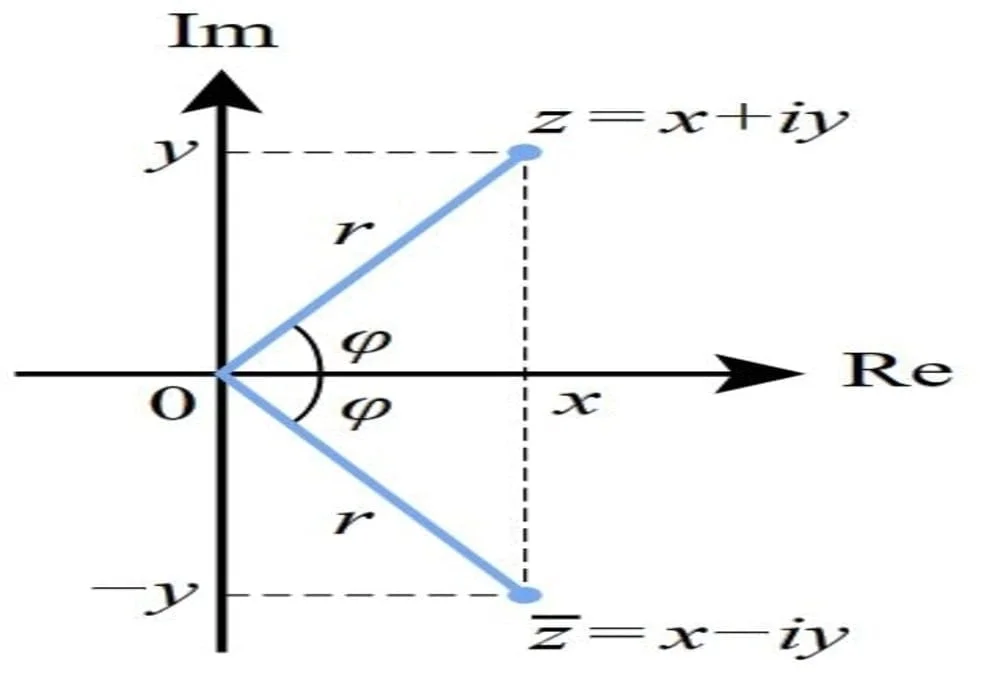
Bentuk Konjugasi

Bentuk konjugat dari angka kompleks $z = x + yi$ didefinisikan sebagai $x - yi$ . Hal ini dilambangkan dengan salah satu seperti ${\overline {z}}$ atau $z *$ .

Secara geometris, ${\bar {z}}$ is the “reflection” of $z$ tentang sumbu sebenarnya. Konjugasi dua kali memberikan bilangan kompleks asli: ${\bar {\bar {z}}}=z$ .

Bagian nyata dan imajiner dari bilangan kompleks z dapat diekstraksi menggunakan konjugat:

\operatorname {Re} (z)={\dfrac {z+{\overline {z}}}{2}},\,

\operatorname {Im} (z)={\dfrac {z-{\overline {z}}}{2i}}.\,

Selain itu, bilangan kompleks adalah nyata jika dan hanya jika sama dengan konjugatnya sendiri.

Konjugasi mendistribusikan operasi aritmatika standar:

{\overline {z+w}}={\overline {z}}+{\overline {w}},\,

{\overline {z-w}}={\overline {z}}-{\overline {w}},\,

{\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}},\,

{\overline {z/w}}={\overline {z}}/{\overline {w}}.\,

Contoh Soal dan Jawaban Bilangan Kompleks

1. Suatu bilangan kompleks z dinotasikan sebagai z = (x + y).
Jika z = , tentukan x dan y. Lalu, gambarkan z dalam bidang kompleks!

Jawaban:
Bentuk z diubah dulu atau disederhanakan…
z =
z =
z =
z =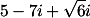
z =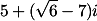
Di sini didapat bahwa x=5 dan y = .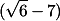
Ini adalah lokasi titik z di bidang kompleks:

Titik yang berwarna merah adalah titik yang dimaksud.

2. Jika z1 = z2 = z3.
z1 = c + a.
z2 = b + 2c.
z3 = a+2 – d.
Tentukan a, b, c, d dan z1, z2 dan z3!

Jawab:
Di sini, kita harus tahu bahwa 2 bilangan kompleks p + q dan r+sdikatakan sama jika dan hanya jika p = r DAN q = s.

Oleh karena itu, kita tinggal menghubung-hubungkan koefisiennya..

z1 = z2 = z3

c + a

= b + 2c

= a+2 – d

c = b = a+2 … (i)
a = 2c = -d … (ii)

c= a+2
Substitusikan nilai c ke persamaan 2
a = 2(a+2)
a = 2a + 4
a = -4
Jadi, kita dapatkan nilai d = 4. c=-2. b = -2. (Substitusi biasa)

Kita dapatkan z1 = z2 = z3 = c + a = -2 -4.

3. Soal penambahan: (3+2)+(-2+7) =…

Jawaban:
(3+2)+(-2+7) = 3 + 2 -2 + 7 = 1 + 9.

4. Soal pengurangan: (2-3)-(8-2)=…

Jawaban:
Dikerjakan sama seperti penjumlahan..
(2-3)-(8-2) = 2 -3 -8 +2 = -6 –.

5. Soal perkalian: (3+4)(2-5) = …

Jawaban:
Lakukan perkalian biasa terlebih dahulu.
(3+4)(2-5) = 6 -15 + 8 -20.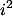
Lalu ubah 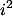menjadi 1.(3+4)(2-5) = 6 -15 + 8 +20 = 26 -7.

6. Soal pembagian:

= ….
Jawaban:
Lihat bagian penyebut, yaitu 3+4i. Maka, sekawan/konjugatnya adalah 3-4i. Kalikan bilangan konjugat ini di pembilang dan penyebut. (lihat langkah di bawah).
=
====-=
====-=
====-=
====-=

7. Soal pemangkatan sederhana: Jika z = 3-. Tentukan .

Jawaban:
Hasil dari pemangkatan dapat diselesaikan dengan dalil De Moivre. Namun, karena kita belum belajar hal itu, kita akan mengalikannya secara biasa.
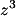= (3-)(3-)(3-) = (9-6-1)(3-)=(8-6)(3-)=24-8-18-6=18-27.

8. Tambahkan bilangan kompleks 3 + 2i dan 1 + 7i:

Jawaban:

tambahkan bilangan real, dan tambahkan bilangan imajiner:
(3 + 2i) + (1 + 7i)
= 3 + 1 + (2 + 7)i
= 4 + 9i

9. Mengingat bilangan akar bilangan kompleks: z = -2 + 7i adalah akar dari persamaan: z³ + 6 z² + 61 z + 106 = 0
temukan akar sebenarnya dari persamaan tersebut.

Jawaban:

Karena z = -2 + 7i adalah akar persamaan dan semua koefisien dalam persamaan tersebut adalah bilangan real, maka z ‘konjugasi kompleks dari z juga merupakan solusi. Maka:
z³ + 6 z² + 61 z + 106 = (z – (-2 + 7i))(z – (-2 – 7i)) q(z)
= (z² + 4z + 53) q(z)
q(z) = [ z³ + 6 z² + 61 z + 106 ] / [ z² + 4z + 53 ] = z + 2
Z + 2 adalah faktor z³ + 6 z² + 61 z + 106 dan oleh karena itu z = -2 adalah akar sebenarnya dari persamaan yang diberikan.

10. Selesaikan soal ini: a) Tunjukkan bahwa bilangan kompleks 2i adalah akar persamaan: z⁴ + z³ + 2 z² + 4 z – 8 = 0
b) Temukan semua akar dari persamaan ini.

Jawaban:

a) (2i)⁴ + (2i)³ + 2 (2i)² + 4 (2i) – 8
= 16 – 8i – 8 + 8i – 8 = 0

b) 2i adalah root -2i juga merupakan root (konjugasi kompleks karena semua koefisien adalah nyata).
z⁴ + z³ + 2 z² + 4 z – 8 = (z – 2i)(z + 2i) q(z)
= (z² + 4)q(z)
q(z) = z² + z – 2
Dua akar persamaan lainnya adalah akar dari q(z): z = 1 and z = -2.

Quiz Matematika Tersulit (Berani mencobanya?)

Jenis Bilangan Matematika: Asli, Prima, Ganjil, Genap, Rasional, Irrasional, Imajiner, Komposit, Kompleks, Romawi…

Klik disini untuk membaca tentang bilangan matematika lainnya. (Akan membuka layar baru, tanpa meninggalkan layar ini).

Artikel Matematika Lainnya

Bacaan Lainnya

Sumber bacaan: Cleverly Smart, Wikipedia, Math is Fun, Brilliant, Wolfram

Rumus Bilangan Kompleks – Contoh Soal dan Jawaban