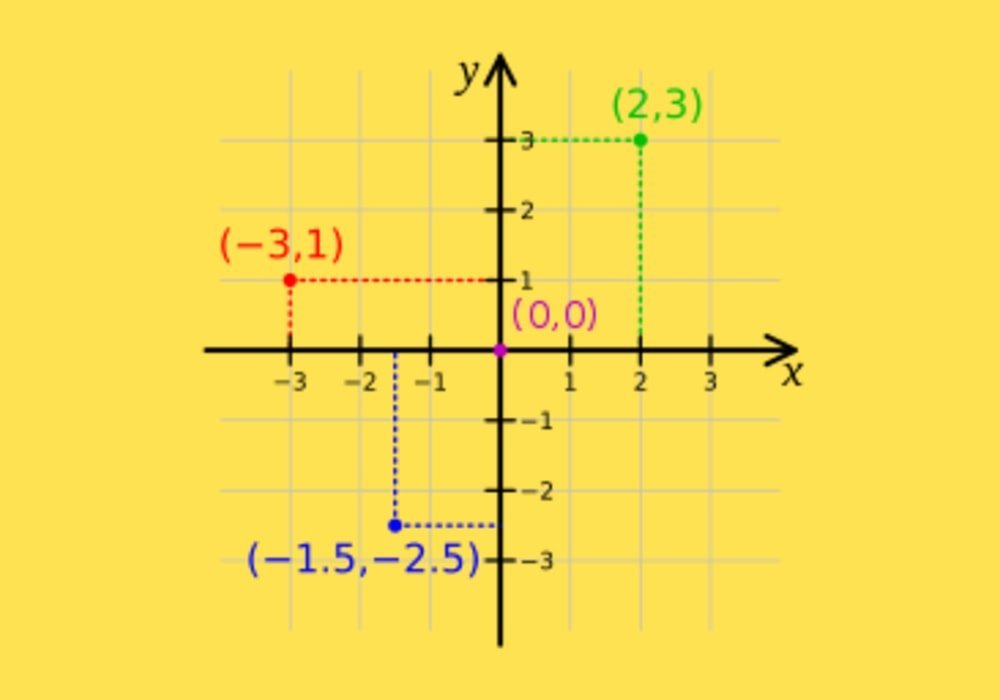
Koordinat Kartesius
Dalam koordinat kartesius, grafik dari persamaan kuadrat dengan dua variabel selalu menghasilkan irisan kerucut, dan semua irisan kerucut dapat dihasilkan dengan cara ini.
Jika terdapat persamaan dengan bentuk:
- {
maka:
- Jika h2 = ab, persamaan ini menghasilkan parabola.
- Jika h2 < ab, persamaan ini menghasilkan elips.
- Jika h2 > ab, persamaan ini menghasilkan hiperbola.
- Jika a = b dan h = 0, persamaan ini menghasilkan lingkaran.
- Jika a + b = 0, persamaan ini menghasilkan hiperbola persegi.
Cara mencari koordinat kartesius
Cara menentukan posisi titik dari koordinat kartesius:
1. Mencari koordinat x dengan cara menarik garis lurus dari titik ke arah atas/ bawah (vertikal) menuju sumbu-x, kemudian lihat menyentuh angka berapa.
2. Mencari koordinat y dengan cara menarik garis lurus dari titik ke arah kiri/ kanan (horizontal) menuju sumbu-y, kemudian lihat menyentuh angka berapa.
Koordinat kartesius adalah
Simstem koordinat untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x dan koordinat y dari titik tersebut.
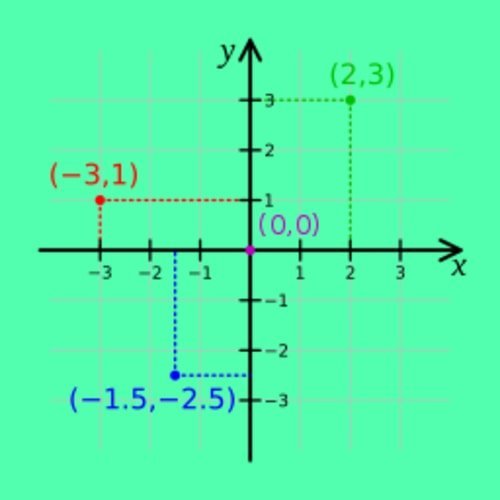
Sistem Koordinat Kartesius
Dalam matematika, Sistem koordinat Kartesius digunakan untuk menentukan tiap titik dalam bidang dengan menggunakan dua bilangan yang biasa disebut koordinat x (absis) dan koordinat y (ordinat) dari titik tersebut.
Untuk mendefinisikan koordinat diperlukan dua garis berarah yang tegak lurus satu sama lain (sumbu x dan sumbu y), dan panjang unit, yang dibuat tanda-tanda pada kedua sumbu tersebut (lihat Gambar 1).
Sistem koordinat Kartesius dapat pula digunakan pada dimensi-dimensi yang lebih tinggi, seperti 3 dimensi, dengan menggunakan tiga sumbu (sumbu x, y, dan z).
Dengan menggunakan sistem koordinat Kartesius, bentuk-bentuk geometri seperti kurva dapat diekspresikan dengan persamaan aljabar. Sebagai contoh, lingkaran yang berjari-jari 2 dapat diekspresikan dengan persamaan x² + y² = 4 (lihat Gambar 2).
Istilah Kartesius digunakan untuk mengenang ahli matematika sekaligus filsuf dari Prancis Descartes, yang perannya besar dalam menggabungkan aljabar dan geometri (Cartesius adalah latinisasi untuk Descartes). Hasil kerjanya sangat berpengaruh dalam perkembangan geometri analitik, kalkulus, dan kartografi.
Ide dasar sistem ini dikembangkan pada tahun 1637 dalam dua tulisan karya Descartes. Pada bagian kedua dari tulisannya Discourse on the Method, ia memperkenalkan ide baru untuk menggambarkan posisi titik atau objek pada sebuah permukaan, dengan menggunakan dua sumbu yang bertegak lurus antar satu dengan yang lain. Dalam tulisannya yang lain, La Géométrie, ia memperdalam konsep-konsep yang telah dikembangkannya.
Lihat koordinat untuk sistem-sistem koordinat lain seperti sistem koordinat polar.
Garis bilangan, Sistem koordinat 1 dimensi
Garis bilangan (bahasa Inggris: number line) dalam matematika dasar adalah suatu gambar garis lurus di mana setiap titiknya diasumsikan melambangkan suatu bilangan real dan setiap bilangan real merujuk pada satu titik tertentu.
Seringkali bilangan bulat ditunjukkan dengan lambang titik-titik tertentu yang berjarak sama di sepanjang garis ini.
Misalnya, gambar di bawah ini menunjukkan bilangan bulat dari −9 sampai 9. Meskipun demikian, garis ini mencakup semua bilangan real, berkelanjutan tak terhingga ke kedua arahnya, dan juga bilangan-bilang tak bertanda yang terdapat di antara bilangan-bilangan bulat itu. Biasanya digunakan sebagai alat bantu dalam mengajar penjumlahan dan pengurangan sederhana, khususnya yang melibatkan bilangan negatif.
Garis di atas dibagi menjadi dua belahan simetri oleh titik nol (origin), yaitu yang melambangkan bilangan nol.
Dalam matetmatika lanjutan, ekspresi “garis bilangan real” (real number line atau real line) biasanya dipakai untuk melambangkan konsep di atas, yaitu setiap titik pada garis lurus ini melambangkan satu bilangan real tertentu, dan vice versa (“sebaliknya”).
Sistem koordinat 2 dimensi
Sistem koordinat Kartesius dalam dua dimensi umumnya didefinisikan dengan dua sumbu yang saling bertegak lurus antar satu dengan yang lain, yang keduanya terletak pada satu bidang (bidang xy). Sumbu horizontal diberi label x, dan sumbu vertikal diberi label y. Pada sistem koordinat tiga dimensi, ditambahkan sumbu yang lain yang sering diberi label z. Sumbu-sumbu tersebut ortogonal antar satu dengan yang lain. (Satu sumbu dengan sumbu lain bertegak lurus.)
Titik pertemuan antara kedua sumbu, titik asal, umumnya diberi label 0. Setiap sumbu juga mempunyai besaran panjang unit, dan setiap panjang tersebut diberi tanda dan ini membentuk semacam grid. Untuk mendeskripsikan suatu titik tertentu dalam sistem koordinat dua dimensi, nilai x ditulis (absis), lalu diikuti dengan nilai y (ordinat). Dengan demikian, format yang dipakai selalu (x,y) dan urutannya tidak dibalik-balik.
Pilihan huruf-huruf didasari oleh konvensi, yaitu huruf-huruf yang dekat akhir (seperti x dan y) digunakan untuk menandakan variabel dengan nilai yang tak diketahui, sedangkan huruf-huruf yang lebih dekat awal digunakan untuk menandakan nilai yang diketahui.
Sebagai contoh, pada Gambar 3, titik P berada pada koordinat (3,5).
Karena kedua sumbu bertegak lurus satu sama lain, bidang xy terbagi menjadi empat bagian yang disebut kuadran, yang pada Gambar 3 ditandai dengan angka I, II, III, dan IV. Menurut konvensi yang berlaku, keempat kuadran diurutkan mulai dari yang kanan atas (kuadran I), melingkar melawan arah jarum jam (lihat Gambar 3). Pada kuadran I, kedua koordinat (x dan y) bernilai positif. Pada kuadran II, koordinat x bernilai negatif dan koordinat y bernilai positif. Pada kuadran III, kedua koordinat bernilai negatif, dan pada kuadran IV, koordinat x bernilai positif dan y negatif (lihat tabel di bawah ini).
| Kuadran | nilai x | nilai y |
|---|---|---|
| I | > 0 | > 0 |
| II | < 0 | > 0 |
| III | < 0 | < 0 |
| IV | > 0 | < 0 |
Sistem koordinat 3 dimensi
3 dimensi atau biasa disingkat 3D atau disebut ruang, adalah bentuk dari benda yang memiliki panjang, lebar, dan tinggi.
Istilah ini biasanya digunakan dalam bidang seni, animasi, komputer dan matematika. Setiap bangun 3 dimensi memiliki kapasitas, disebut juga dengan volume.
Gradien
Gradien (bahasa Inggris: gradient) dalam matematika adalah salah satu operator dalam kalkulus vektor yang berguna untuk mencari perubahan arah dan kecepatan dalam bidang skalar. Dalam matematika, gradien didefinisikan sebagai:
Sebagai contoh dalam sistem koordinat Kartesius tiga dimensi, gradien dari suatu vektor adalah:
Contoh Soal Koordinat Kartesius
Diketahui garis p dan q merupakan dua garis lurus yang tidak mempunyai titik potong walaupun telah diperpanjang hingga tak terhingga.
Kedudukan dari garis p dan q yaitu…
a. Berimpit
b. Sejajar
c. Bersilangan
d. Berpotongan
Jawab:
Dua buah garis yang tidak mempunyai titik potong walaupun diperpanjang merupakan dua garis yang saling sejajar.
Jawaban yang tepat adalah B.
Perhatikan garis g pada koordinat Cartesius. Garis k tegak lurus garis g dan saling berpotongan di titik (0,-20). Koordinat titik potong garis k dengan sumbu-x adalah…

A. (8,0)
B. (12,0)
C. (16,0)
D. (20,0)
Jawaban : C
titik (-25,0) (0,-20)
gradien = -20 / 25 = -4/5
gradien yang tegak lurus = -1 : -4/5 = 5/4
titik potong (0,-20)
persamaan garis k :
y + 20 = 5/4 (x – 0)
y + 20 = 5/4 x
titik potong garis k terhadap sumbu x :
y = 0
y + 20 = 5/4 x
20 = 5/4 x
80 = 5x
x = 16
titik potong = (16,0)
Untuk koordinat kartesius ke koordinat kutub koordinat kutub titik (-4,4) adalah…
penyelesaian :
(x,y)⇒ (r, α)
x = -4, y=4
(karena x negatif dan y positif, maka α sudut di kuadran II)
tan α = x/y
⇒4/ – 4
⇒ – 1
karena α sudut di kuadran II, maka : α = (180-45)°= 135°
maka koordinat kutubnya ialah ( 4√2, 135°)
Komplemen dari sudut 48 dejarat yaitu…
a. 42°
b. 52°
c. 68°
d. 138°
Jawab:
Komplemen = 90 – 48 = 42
Jawaban yang benar adalah A.
Koordinat kutub suatu titik (4,45 derajat) koordinat cartesius titik tersebut adalah…
X = r.cosα = 4.cos45 = 4.1/2√2 = 2√2
y = r.sinα = 4.sin45 = 4.1/2√2 = 2√2
(x,y) = (2√2,2√2)
Besar <P = 113 derajat maka sudut P adalah sudut…
a. Refleks
b. Tumpul
c. Siku-siku
d. Lancip
Jawab:
Sudut P besarnya 113 derajat, yang berarti sudut P merupakan sudut tumpul.
Sebab sudut tumpul merupakan sudut yang berada dalam kisaran 90 derajat sampai 180 derajat.
Jawaban yang benar adalah B.
Besar sudut pada jarum jam saat menunjukkan pukul 03.00 adalah…
a. 180°
b. 90°
c. 60°
d. 30°
Jawab:
Pada saat pukul 03.00, jarum pendek akan menunjuk pada angka 3 sedangkan jarum panjang akan menunjuk angka 12, oleh karena itu sudut yang dibentuk yaitu 90 derajat.
Jawaban yang benar adalah B.
Mengubah atau Mengkonversi Koordinat Polar ke Koordinat Kartesius. Koordinat kartesius dari titik (10, 315°) adalah…
A. (-5, -5√2)
B. (-5, 5√2)
C. (5√2, 5√2)
D. (5√2, -5√2)
E. (5, -5√2)
Jawab : D
» Sudut 315° (kuadran IV) —–> (x, -y)
» Dari pilihan jawaban di atas maka kemungkinan jawabannya D atau E
» (r, α) ——> (10, 315°)
x = 10 . cos 315°
x = 10 . ½√2
x = 5√2
y = 10 . sin 315°
y = 10 . -½√2
y = -5√2
Jadi koordinat kartesiusnya adalah (5√2, -5√2)
Untuk lebih jelas dapat dilihat pada gambar di samping.
Mengubah atau Mengkonversi Koordinat Kartesius ke Koordinat Polar. Koordinat kutup dari titik (-6, 6√3) adalah…
A. (12, 30°)
B. (12, 60°)
C. (12, 90°)
D. (12, 120°)
E. (12, 210°)
Jawab : D
Cara biasa
r² = (-6)² + (6√3)²
r² = 36 + 108
r² = 144
r = 12
a = arc tan (6√3) / -6
a = arc tan -√3
a = 120°
Jadi koordinat kutubnya adalah (12, 120°)
Cara praktis
» (-6, 6√3) ——-> (-x, y) —–> maka berada di kuadran II
» Dari pilihan jawaban di atas yang berada di kuadran II yaitu hanya pilihan D
» Sedangkan r tidak usah dicari karena dari pilihan jawaban semuanya sama.
Bacaan Lainnya
- Induksi Elektromagnetik – Hukum Faraday dan Hukum Lenz – Soal dan Jawaban
- Induksi dan Fluks Magnetik Bersama Contoh Soal dan Jawaban
- Rumus Rangkaian Listrik Dan Contoh-Contoh Soal Beserta Jawabannya
- Tabel Konstanta Fisika – Tabel konstanta universal, elektromagnetik, atom dan nuklir, fisika-kimia, nilai yang diadopsi, satuan natural, bilangan tetap
- Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Cara Mengemudi Aman Pada Saat Mudik atau Liburan Panjang
- Jenis Virus Komputer – Cara Gratis Mengatasi Dengan Windows Defender
- Cara Menghentikan Penindasan Bullying
- Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
- Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
- Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
- Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Apakah Produk Pembalut Wanita Aman?
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Lumen Learning, Math is Fun
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing