Persamaan Pangkat 3

Bentuk umum dari persamaan pangkat 3 adalah ax³ + bx² + cx + d = 0  dengan a ≠ 0

Persamaan ini memiliki 3 akar

Untuk mendapatkan akarnya ada 3 cara yang bisa dilakukan

1. Memfaktorkan

2. Menyederhanakan menjadi persamaan kuadrat

3. Menggunakan rumus

Fungsi Kubik (Fungsi Pangkat 3)

Dalam matematika, sebuah fungsi kubik atau lebih dikenal sebagai fungsi pangkat tiga adalah suatu fungsi yang memiliki bentuk

dengan a bernilai tidak nol; atau dengan kata lain merupakan suatu polinomial orde tiga. Turunan dari suatu fungsi kubik adalah suatu fungsi kuadrat. Integral dari suatu fungsi kubik adalah fungsi pangkat empat (kuartik).

Menetapkan ƒ(x) = 0 menghasilkan persamaan kubik dengan bentuk:

Biasanya, koefisien a, b, c, dan d merupakan bilangan riil. Untuk menyelesaikan persamaan kubik, caranya dengan mencari akar (nilai nol) dari fungsi kubik.

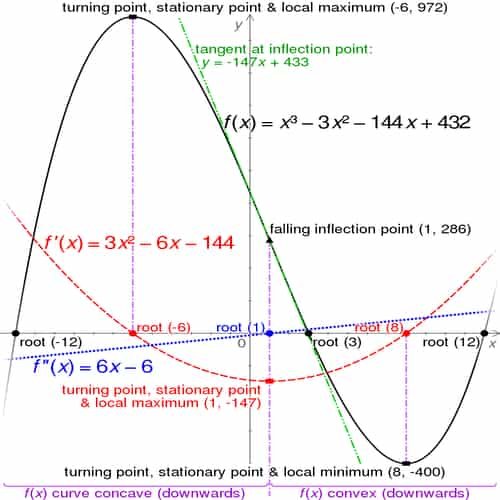
Titik puncak dan titik belok

Titik puncak suatu fungsi adalah ketika gradien atau turunan pertama fungsi itu sama dengan nol.

Titik puncak fungsi kubik:

adalah fungsi kuadrat:

sedangkan titik beloknya diberikan rumus:

Cara Menyelesaikan Persamaan Pangkat 3

Car 1. Memfaktorkan

Cara ini biasanya hanya dipakai untuk mencar akar-akar rasional.

Cara 2. Menggunakan Pendekatan Diskriminan

1. Tuliskan persamaan a, b, c, dan d

Untuk mencari jawaban persamaan kubik dengan cara ini, kita akan banyak melakukan perhitungan dengan koefisien dalam persamaan kita. Karena hal ini, sebaiknya Anda mencatat nilai a, b, c, dan d sebelum Anda lupa salah satu nilainya.

• • Sebagai contoh, untuk persamaan x³ – 3x² + 3x – 1, tuliskanlah menjadi a = 1, b = -3, c = 3, dan d = -1. Jangan lupa bahwa saat variabel x tidak memiliki koefisien, maka nilainya adalah 1.

2. Hitung Δ0 = b² – 3ac

Pendekatan diskriminan untuk mencari jawaban dari persamaan kubik membutuhkan perhitungan yang rumit, tetapi jika Anda mengikuti langkahnya dengan hati-hati, pendekatan ini akan sangat bermanfaat untuk menyelesaikan persamaan kubik yang sulit dipecahkan dengan cara lain. Untuk memulainya, carilah nilai Δ0, yang merupakan nilai penting pertama dari beberapa yang kita perlukan, dengan memasukkan nilai yang sesuai ke dalam rumus b² – 3ac.

• • Dalam contoh yang kita gunakan, kita akan menyelesaikannya sebagai berikut:

  • b² – 3ac
  • (-3)² – 3(1)(3)
  • 9 – 3(1)(3)
  • 9 – 9 = 0 = Δ0

3. Hitung Δ1= 2b³ – 9abc + 27a²d

Nilai penting selanjutnya yang kita butuhkan, Δ1, memerlukan perhitungan yang lebih panjang, tetapi dapat diketahui dengan cara yang sama seperti Δ0. Masukkan nilai yang sesuai ke dalam rumus 2b³ – 9abc + 27a²d untuk mendapatkan nilai Δ1.

• • Dalam contoh ini, kita menyelesaikannya sebagai berikut:

2(-3)³ – 9(1)(-3)(3) + 27(1)²(-1)

2(-27) – 9(-9) + 27(-1)

-54 + 81 – 27

81 – 81 = 0 = Δ1

4. Hitung Δ = Δ1² – 4Δ0³) ÷ -27a².

Selanjutnya, kita hitunng nilai “diskriminan” dari nilai Δ0 dan Δ1. Diskriminan adalah angka yang memberikan Anda informasi mengenai akar polinomial (Anda mungkin telah hafal secara tidak sadar rumus diskriminan kuadrat: b² – 4ac). Dalam kasus persamaan kubik, jika nilai diskriminan positif, maka persamaan tersebut memiliki tiga jawaban bilangan riil. Jika nilai diskriminan sama dengan nol, maka persamaan tersebut memiliki satu atau dua jawaban bilangan riil, dan beberapa jawaban di antaranya bernilai sama. Jika nilainya negatif, maka persamaan tersebut hanya memiliki satu jawaban bilangan riil, karena grafik persamaan akan selalu memotong sumbu x paling tidak satu kali.)

• • Dalam contoh ini, karena baik nilai Δ0 dan Δ1 = 0, mencari nilai Δ akan sangat mudah dilakukan. KIta hanya perlu menghitungnya dengan cara berikut ini:

Δ1² – 4Δ0³) ÷ -27a²

(0)² – 4(0)³) ÷ -27(1)²

0 – 0 ÷ 27

0 = Δ, jadi persamaan kita memiliki 1 atau 2 jawaban.

5. Hitung C = ³√(√((Δ1² – 4Δ0³) + Δ1)/ 2)

Nilai terakhir yang penting untuk kita dapatkan adalah nilai C. Nilai ini memungkinkan kita untuk mendapatkan ketiga akar dari persamaan kubik kita. Selesaikan seperti biasanya, masukkan nilai Δ1 dan Δ0 ke dalam rumus.

• • Dalam contoh ini, kita akan mendapatkan nilai C dengan cara:

³√(√((Δ1² – 4Δ0³) + Δ1)/ 2)

³√(√((0² – 4(0)³) + (0))/ 2)

³√(√((0 – 0) + (0))/ 2)

0 = C

6. Hitung ketiga akar persamaan dengan variabel Anda

Akar (jawaban) dari persamaan kubik Anda ditentukan dengan rumus (b + uⁿC + (Δ0/uⁿC)) / 3a, di mana u = (-1 + √(-3))/2 dan n sama denagn 1, 2, atau 3. Masukkan nilai Anda ke dalam rumus untuk menyelesaikannya — mungkin perhitungan yang perlu Anda selesaikan cukup banyak, tetapi Anda seharusnya akan mendapatkan ketiga jawaban persamaan kubik Anda!

• • Dalam contoh ini, kita mungkin menyelesaikannya dengan memeriksa jawaban saat n sama dengan 1, 2, dan 3. Jawaban yang kita dapatkan dari perhitungan ini adalah kemungkinan jawaban dari persamaan kubik kita — nilai apa pun yang kita masukkan ke dalam persamaan kubik dan memberikan hasil sama dengan 0, adalah jawaban yang benar. Sebagai contohnya, jika kita mendapatkan jawaban sama dengan 1 jika dalam salah satu percobaan perhitungan kita, dengan memasukkan nilai 1 ke dalam persamaan x³ – 3x² + 3x – 1 menghasilkan hasil akhir sama dengan 0. Dengan demikian 1 merupakan salah satu jawaban dari persamaan kubik kita.

Cara 3. Menyelesaikan Menggunakan Persamaan Kuadrat

1. Periksa apakah persamaan kubik Anda memiliki konstanta

Sebagaimana dinyatakan di atas, bentuk persamaan kubik adalah ax³ + bx² + cx + d = 0. b, c, dan nilai d bisa jadi 0 tanpa mempengaruhi bentuk persamaan kubik ini; hal ini pada dasarnya berarti bahwa persamaan kubik tidak harus selalu menyertakan nilai bx², cx, atau d untuk bisa menjadi sebuah persamaan kubik. Untuk mulai menggunakan cara yang cukup mudah dalam memecahkan persamaan kubik ini, periksalah apakah persamaan kubik Anda memiliki sebuah konstanta (atau nilai d). Jika persamaan Anda tidak memiliki konstanta atau nilai d, maka Anda dapat menggunakan persamaan kuadrat untuk mencari jawaban dari persamaan kubik setelah melakukan beberapa langkah perhitungan.

• • Di sisi lain, jika persamaan Anda memiliki nilai konstanta, maka Anda akan membutuhkan cara penyelesaian yang lainnya. Lihat langkah di bawah untuk mengetahui pendekatan lainnya.

2. Faktorkan nilai x dari persamaan kubik

Karena persamaan Anda tidak memiliki nilai konstanta, semua komponen di dalamnya memiliki variabel x. Hal ini berarti, nilai x ini dapat difaktorkan keluar dari persamaan untuk menyederhanakannya. Lakukan langkah ini dan tulis ulang persamaan kubik Anda dalam bentuk x(ax² + bx + c).

• • Sebagai contohnya, katakanlah bahwa persamaan kubik asal di sini adalah 3x³ + -2x² + 14x = 0. Dengan memfaktorkan satu variabel x dari persamaan ini, kita akan mendapatkan persamaan x(3x² + -2x + 14) = 0.

3. Gunakan persamaan kuadrat untuk memecahkan persamaan yang berada di dalam tanda kurung

Kalian mungkin menyadari bahwa sebagian persamaan baru Anda, yang terdapat di dalam tanda kurung, berbentuk persamaan kuadrat (ax² + bx + c). Hal ini berarti kita dapat mencari nilai yang dibutuhkan agar hasil persamaan ini sama dengan nol dengan memasukkan a, b, dan c ke dalam rumus persamaan kuadrat ({-b +/-√ (b²– 4ac)}/2a). Lakukan perhitungan ini untuk mencari dua jawaban dari persamaan kubik Anda.

4. Gunakanlah nol dan jawaban persamaan kuadrat Anda sebagai jawaban persamaan kubik Anda

Contoh Soal dan jawaban Persamaan Pangkat 3

1. Soal: Nilai x yang memenuhi persamaan 1-8x=-4x-15 adalah…

Jawaban:

1-8x=-4x-15
-8x+4x=-15-1
-4x=-16
x=-16/-4=4

2. Tentukan himpunan penyelesaian dari persamaan pangkat 3 berikut ini: x³ – 5x² – 2x + 10 = 0

Jawaban:

x³ – 5x² – 2x + 10 = 0
x² ( x – 5) – 2(x – 5) = 0
(x² – 2)(x – 5) = 0
(x+√2) (x-√2) (x-5) = 0
x= -√2 atau x= √2 atau x=5

Jadi himpunan penyelesaiannya adalah {-√2, √2,5}

3. Tentukan himpunan penyelesaian dari persamaan pangkat 3 berikut ini: x³ – 7x² + 10x  = 0

Jawaban:

x³ – 7x² + 10x  = 0
x(x² – 7x + 10)  = 0
x(x – 2)(x – 5) = 0
x = 0 atau x = 2 atau x = 5

Jadi himpunan penyelesaiannya adalah {0, 2, 5}

4. Tentukan himpunan penyelesaian dari persamaan pangkat 3 berikut ini: x³ – 3x² – 4x + 12 = 0

Jawaban:

x³ – 3x² – 4x + 12 = 0
x² (x – 3) – 4(x – 3) = 0
(x² – 4)(x – 3)= 0
(x – 2)(x + 2)(x – 3) = 0
x = 2 atau x = -2 atau x = 3

Jadi himpunan penyelesaiannya adalah  {-2, 2, 3}

5. Tentukan himpunan penyelesaian dari: x³ – 5x² – 25x + 125 = 0

Jawaban:

x³ – 5x² – 25x + 125 = 0
x² (x – 5) – 25(x – 5) = 0
(x² – 25) (x – 5) = 0
(x – 5)(x + 5)(x – 5) = 0
x = 5 atau x = -5 atau x = 5

Jadi himpunan penyelesaiannya adalah  {-5, 5}

6. Tentukan himpunan penyelesaian dari: 3x³ – x² + 6x – 2 = 0

Jawaban:

3x³ – x² + 6x – 2 = 0
x² (3x – 1) + 2(3x – 1) = 0
(x² + 2)(3x – 1) = 0
x² = – 2 (tidak mungkin)
x = 1/3

Jadi himpunan penyelesaiannya adalah {1/3}

7. Tentukan himpunan penyelesaian dari x³ – 3x² – 5x + 15 = 0

Jawaban:

x³ – 3x² – 5x + 15 = 0
x²(x – 3) – 5(x – 3) = 0
(x² – 5)(x – 3) = 0
Jadi himpunan penyelesaian dari persamaan berikut ialah {√5, -√5, 3}

8. Tentukan himpunan penyelesaian dari x³ – x² – 4x = 0

Jawaban:

x³ – x² – 12x = 0
x(x² – x – 12) = 0
x(x- 4)(x + 3) = 0
x = 0 atau x = 4 atau x = -3
Jadi himpunan penyelesaian dari persamaan tersebut ialah {-3, 0, 4}.

Bacaan Lainnya

• Persamaan Kuadrat – Rumus Kuadratis (Rumus abc), Pembuktian rumus persamaan kuadrat, Diskriminan/determinan, Akar riil dan kompleks, Geometri, Rumus fungsi kuadrat
• Pangkat Eksponen- Integer – Daftar eksponensial bilangan bulat dan contoh soal dan jawaban
• Quiz Matematika- 4√16 + 4√16 = jawaban A, B, C atau D ? ‪- Penyederhanaan Akar Kuadrat
• Pangkat Matematika – Tabel dari 1-100 – Pangkat 2, 3, Akar Pangkat 2 dan 3 – Beserta Contoh Soal dan Jawaban
• Nilai Pi 1 juta digit pertama π
• Nilai Pi Yang Tepat π – 100 000 digit pertama
• Perbandingan Rasio Matematika – Rumus, Contoh Soal dan Jawaban
• Faktoradik Matematika – Nilai, Cara, Kode Program dan Contohnya
• Rumus Geometri – Contoh Soal dan Jawaban – Segi tiga, Persegi, Trapesium, Layang-layang, Jajaran Genjang, Belah ketupat, Lingkaran, Prisma, Balok, Kubus, Tabung, Limas, Bola
• Rumus Volume (Isi) Matematika – rumus volume untuk: kubus, balok, silinder, limas, kerucut, bola, ellipsoid, torus, tetrahedron, tarallelepiped, volume benda putar…
• Sudut Matematika dan Radian – Geometri – Soal Jawaban
• Rumus Turunan Matematika – TABEL TURUNAN DIFERENSIAL KALKULUS – Beserta Contoh Soal dan Jawaban
• Rumus-Rumus Lingkaran – Volume – Tes Matematika Lingkaran
• Induksi Elektromagnetik – Hukum Faraday dan Hukum Lenz – Soal dan Jawaban
• Rumus Induktansi, Induktor dan Energi Medan Magnet – Soal dan Jawaban
• Induksi dan Fluks Magnetik Bersama Contoh Soal dan Jawaban
• Rumus Rangkaian Listrik Dan Contoh-Contoh Soal Beserta Jawabannya
• Tabel Konstanta Fisika – Tabel konstanta universal, elektromagnetik, atom dan nuklir, fisika-kimia, nilai yang diadopsi, satuan natural, bilangan tetap
• Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
• Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
• Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
• Apakah Produk Pembalut Wanita Aman?
• Sistem Reproduksi Manusia, Hewan dan Tumbuhan
• Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
• Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?

Sumber: California Institute of Technology

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing