Rumus Volume

Volume atau bisa juga disebut kapasitas adalah penghitungan seberapa banyak ruang yang bisa ditempati dalam suatu objek. Objek itu bisa berupa benda yang beraturan ataupun benda yang tidak beraturan. Temukan di bawah ini berbagai rumus volume untuk: kubus, balok, silinder, limas, kerucut, bola, ellipsoid, torus, tetrahedron, tarallelepiped, volume benda putar…

Benda yang beraturan misalnya kubus, balok, silinder, limas, kerucut, dan bola. Benda yang tidak beraturan misalnya batu yang ditemukan di jalan. Volume digunakan untuk menentukan massa jenis suatu benda. Berikut adalah rumus volume untuk:

Bentuk	Rumus volume	Variabel
Kubus	$a^{3}\;$	a = panjang sisi/rusuk
Silinder (Tabung)	$\pi r^{2}h\;$	r = jari-jari alas, h = tinggi
Prisma	$B\cdot h$	B = luas alas, h = tinggi
Balok	$l\cdot w\cdot h$	l = panjang, w = lebar, h = tinggi
Prisma segitiga	${\frac {1}{2}}bhl$	b = panjang dasar segitiga, h = tinggi prisma, l = length of prism or distance between the triangular bases
Bola	${\frac {4}{3}}\pi r^{3}$	r = jari-jari bola di mana merupakan integral luas permukaan bola
Ellipsoid	${\frac {4}{3}}\pi abc$	a, b, c = semi-axes of ellipsoid
Torus	$(\pi r^{2})(2\pi R)=2\pi ^{2}Rr^{2}$	r = jari-jari kecil, R = jari-jari besar
Limas	${\frac {1}{3}}Bh$	B = luas alas, h = tinggi limas
Limas persegi	${\frac {1}{3}}s^{2}h\;$	s = sisi samping alas limas, h = tinggi
Limas segiempat	${\frac {1}{3}}lwh$	l = panjang, w = lebar, h = tinggi
Kerucut	${\frac {1}{3}}\pi r^{2}h$	r = jari-jari lingkaran di dasar kerucut, h = jarak dari dasar ke pucuk atau tinggi
Tetrahedron	${{\sqrt {2}} \over 12}a^{3}\,$	panjang sisi $a$
Parallelepiped	$abc{\sqrt {K}}$ ${\begin{aligned}K=&1+2\cos(\alpha )\cos(\beta )\cos(\gamma )\\&-\cos ^{2}(\alpha )-\cos ^{2}(\beta )-\cos ^{2}(\gamma )\end{aligned}}$	a, b, and c are the parallelepiped edge lengths, and α, β, and γ are the internal angles between the edges
Volume benda putar (dibutuhkan kalkulus)	$\int _{a}^{b}A(h)\,\mathrm {d} h$	h = dimensi apapun, A(h) = luasan cross-section tegak lurus terhadap h yang didefinisikan sebagai fungsi posisi sepanjang h. a dan b adalah batas integrasi volume putar. (Berlaku untuk semua bangun jika cross-sectional area nya dapat ditentukan dari h).
Semua benda diputar (dibutuhkan kalkulus)	$\pi \int _{a}^{b}\left({\left[R_{O}(x)\right]}^{2}-{\left[R_{I}(x)\right]}^{2}\right)\mathrm {d} x$	$R_{O}$ dan $R_{I}$ menyatakan fungsi dari jari-jari luar dan jari-jari dalam fungsi, secara berurutan.

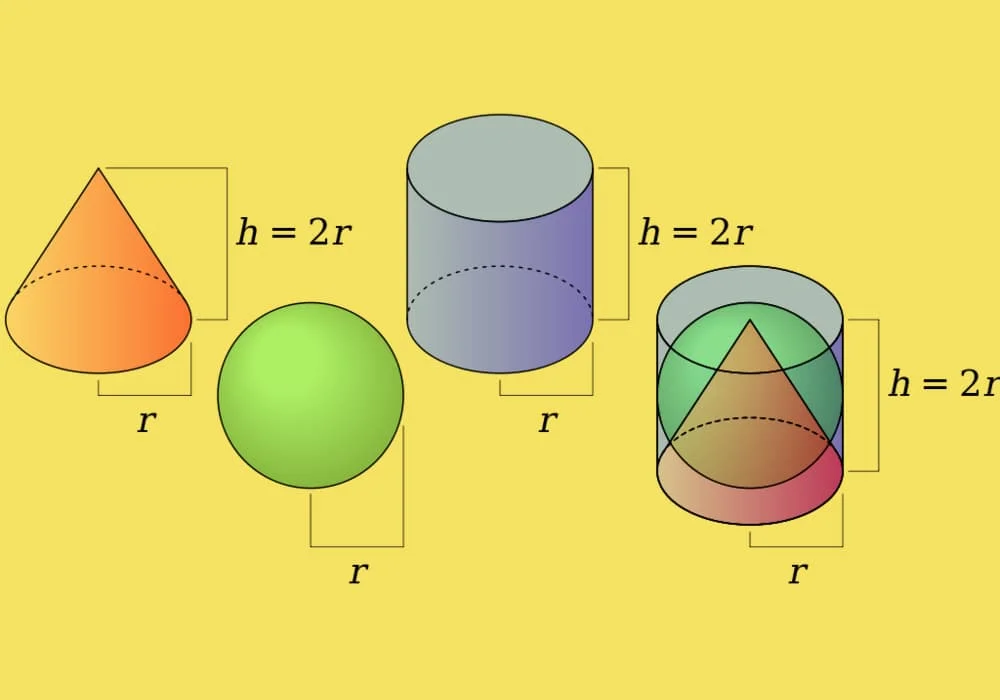
Rumus volume Kerucut, bola, dan silinder dengan jari-jari r dan tinggi h — Rumus-rumus volume: Kerucut, bola, dan silinder dengan jari-jari r dan tinggi h

Rasio volume untuk kerucut, bola, dan silinder dengan tinggi dan jari-jari sama

Rumus di atas dapat digunakan untuk menunjukkan bahwa volume kerucut, bola, dan silinder dengan jari-jari dan tinggi sama memiliki rasio 1 : 2 : 3, seperti berikut ini.

Besar jari-jari dianggap r dan tinggi dianggap h (menjadi 2r untuk bola), maka volume kerucut

{\tfrac {1}{3}}\pi r^{2}h={\tfrac {1}{3}}\pi r^{2}(2r)=({\tfrac {2}{3}}\pi r^{3})\times 1,

volume bola

{\tfrac {4}{3}}\pi r^{3}=({\tfrac {2}{3}}\pi r^{3})\times 2,

sedangkan volume silinder

\pi r^{2}h=\pi r^{2}(2r)=({\tfrac {2}{3}}\pi r^{3})\times 3.

Penemuan rasio volume bola dan silinder 2 : 3 ditemukan oleh Archimedes.

Rumus Volume dalam kalkulus

Pada kalkulus, volume dari sebuah region D dalam R³ adalah integral rangkap tiga dari fungsi konstanta $f(x,y,z)=1$ dan biasanya dituliskan sebagai:

\iiint \limits _{D}1\,dx\,dy\,dz.

Integral volume pada koordinat silinder adalah

\iiint \limits _{D}r\,dr\,d\theta \,dz,

dan integral volume dalam koordinat bola dituliskan sebagai

\iiint \limits _{D}\rho ^{2}\sin \phi \,d\rho \,d\theta \,d\phi .

Satuan volume

Satuan SI volume adalah m³. Satuan lain yang banyak dipakai adalah liter (=dm³) dan ml.

1 m³ = 10³ dm³ = 10⁶ cm³
1 dm³ = 1 l
1 cm³ = 1 ml = 1 cc

Volume dalam termodinamika

Dalam termodinamika, volume dari sebuah sistem termodinamika adalah suatu parameter ekstensif untuk menjelaskan keadaan termodinamika.

Volume spesifik, adalah properti intensif, adalah volume per satuan massa. Volume merupakan fungsi keadaan dan interdependen dengan properti termodinamika lainnya seperti tekanan dan suhu. Contohnya, volume berhubungan tekanan dan suhu gas ideal melalui hukum gas ideal.

Klik disini untuk membaca “Rumus Termodinamika Entropi – Contoh Soal dan Jawaban Termodinamika Entropi“.

Bacaan Lainnya

Sumber bacaan: Math, Basic Mathematics

Rumus Volume (Isi) Matematika – rumus volume untuk: kubus, balok, silinder, limas, kerucut, bola, ellipsoid, torus, tetrahedron, tarallelepiped, volume benda putar…

Rumus Volume

Bentuk

Rumus volume

Variabel

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2f80731f16bb951a9dae465d1def439c3f8e1f89" alt="{\displaystyle a^{3}\;}" />

a = panjang sisi/rusuk

Silinder (Tabung)

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6577ed24266c4e899663056b68646265170e0c4b" alt="{\displaystyle \pi r^{2}h\;}" />

r = jari-jari alas, h = tinggi

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/8546ac33d5cc63f312dc46e7f272cb8a7ff9163f" alt="{\displaystyle B\cdot h}" />

B = luas alas, h = tinggi

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/665d8994ec0ab3a941e4a67728f26fd4e2897bbe" alt="{\displaystyle l\cdot w\cdot h}" />

l = panjang, w = lebar, h = tinggi

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/47fc50cd415fac3454bc46bb086c571ceada78ad" alt="{\displaystyle {\frac {1}{2}}bhl}" />

b = panjang dasar segitiga, h = tinggi prisma, l = length of prism or distance between the triangular bases

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/7112cb504e1399319cb9edbc622d1c4609fd56e3" alt="{\displaystyle {\frac {4}{3}}\pi r^{3}}" />

r = jari-jari bola

di mana merupakan integral luas permukaan bola

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e6bab0d7b6f5d52c794e589223f04011463277e9" alt="{\displaystyle {\frac {4}{3}}\pi abc}" />

a, b, c = semi-axes of ellipsoid

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/73fc04dc08da6df57be7b4961db0d65c6ff434d6" alt="{\displaystyle (\pi r^{2})(2\pi R)=2\pi ^{2}Rr^{2}}" />

r = jari-jari kecil, R = jari-jari besar

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/31fdab0536eaf11c26391cac9ae01644f380e9ee" alt="{\displaystyle {\frac {1}{3}}Bh}" />

B = luas alas, h = tinggi limas

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5bb744ae4843f867f87603bdc2bf46382c54ed37" alt="{\displaystyle {\frac {1}{3}}s^{2}h\;}" />

s = sisi samping alas limas, h = tinggi

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/a5bb53217e5e54687bd78774ee42c4e64d8cbbe0" alt="{\displaystyle {\frac {1}{3}}lwh}" />

l = panjang, w = lebar, h = tinggi

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6d2006a2f5533ecd0dce30332eba227da86b7404" alt="{\displaystyle {\frac {1}{3}}\pi r^{2}h}" />

r = jari-jari lingkaran di dasar kerucut, h = jarak dari dasar ke pucuk atau tinggi

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4981067eb214e485499952bda8fed98775873f94" alt="{\displaystyle {{\sqrt {2}} \over 12}a^{3}\,}" />

panjang sisi <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/ffd2487510aa438433a2579450ab2b3d557e5edc" alt="{\displaystyle a}" />

Parallelepiped

<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f3e4b8b3b1cde51f83356ccc7a33c0ae01c4445d" alt="{\displaystyle abc{\sqrt {K}}}" />

a, b, and c are the parallelepiped edge lengths, and α, β, and γ are the internal angles between the edges

Volume benda putar

(dibutuhkan kalkulus)

h}<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/bf389e165e67594607a07e96126d3b8d16da0067" alt="{\displaystyle \int _{a}^{b}A(h)\,\mathrm {d} h}" />

h = dimensi apapun,

A(h) = luasan cross-section tegak lurus terhadap h yang didefinisikan sebagai fungsi posisi sepanjang h. a dan b adalah batas integrasi volume putar.

(Berlaku untuk semua bangun jika cross-sectional area nya dapat ditentukan dari h).

Semua benda diputar

(dibutuhkan kalkulus)

x}<img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/15f622970c61715e48e9c33088619c89a4bd40e1" alt="{\displaystyle \pi \int _{a}^{b}\left({\left[R_{O}(x)\right]}^{2}-{\left[R_{I}(x)\right]}^{2}\right)\mathrm {d} x}" />

Rasio volume untuk kerucut, bola, dan silinder dengan tinggi dan jari-jari sama

Besar jari-jari dianggap r dan tinggi dianggap h (menjadi 2r untuk bola), maka volume kerucut

volume bola

sedangkan volume silinder

Rumus Volume dalam kalkulus

Integral volume pada koordinat silinder adalah

dan integral volume dalam koordinat bola dituliskan sebagai

Satuan volume

Volume dalam termodinamika

Bacaan Lainnya

Tinggalkan Balasan Batalkan balasan

$a^{3}\;$

$\pi r^{2}h\;$

$B\cdot h$

$l\cdot w\cdot h$

${\frac {1}{2}}bhl$

${\frac {4}{3}}\pi r^{3}$

${\frac {4}{3}}\pi abc$

$(\pi r^{2})(2\pi R)=2\pi ^{2}Rr^{2}$

${\frac {1}{3}}Bh$

${\frac {1}{3}}s^{2}h\;$

${\frac {1}{3}}lwh$

${\frac {1}{3}}\pi r^{2}h$

${{\sqrt {2}} \over 12}a^{3}\,$

panjang sisi $a$

$abc{\sqrt {K}}$

$\int _{a}^{b}A(h)\,\mathrm {d} h$

$\pi \int _{a}^{b}\left({\left[R_{O}(x)\right]}^{2}-{\left[R_{I}(x)\right]}^{2}\right)\mathrm {d} x$