Termodinamika
Adalah fisika energi, panas, kerja, entropi dan kespontanan proses. Termodinamika berhubungan dekat dengan mekanika statistik di mana hubungan termodinamika berasal. Temukan Rumus Termodinamika Entropi di bawah ini.
Dalam bahasa Yunani: thermos = ‘panas’ and dynamic = ‘perubahan’.
Pada sistem di mana terjadi proses perubahan wujud atau pertukaran energi, termodinamika klasik tidak berhubungan dengan kinetika reaksi (kecepatan suatu proses reaksi berlangsung). Karena alasan ini, penggunaan istilah “termodinamika” biasanya merujuk pada termodinamika setimbang. Dengan hubungan ini, konsep utama dalam termodinamika adalah proses kuasistatik, yang diidealkan, proses “super pelan”. Proses termodinamika bergantung-waktu dipelajari dalam termodinamika tak-setimbang.

Pengertian Entropi
Jika makin luas distribusinya, maka semakin tersebara dan kurang teratur strukturnya. Sehingga tingkat ketersediaan energi untuk melakukan usaha semakin rendah. Maka entropi dapat juga dikaitkan dengan tingkat keteraturan sistem dan ketersediaan energi (energi bebas) untuk melakukan usaha.
Rumus Termodinamika
Hukum Termodinamika I
ΔU = Q − W
Keterangan :
ΔU = perubahan energi dalam (joule)
Q = kalor (joule)
W = usaha (joule)
Proses-proses
Isobaris → tekanan tetap
Isotermis → suhu tetap → ΔU = 0
Isokhoris → volume tetap (atau isovolumis atau isometric) → W = 0
Adiabatis → tidak terjadi pertukaran kalor → Q = 0
Siklus → daur → ΔU = 0
Persamaan Keadaan Gas
Hukum Gay Lussac
Tekanan tetap → V/T = Konstan → V1/T1 = V2/T2
Hukum Charles
Volume tetap → P/T = Konstan → P1/T1 = P2/T2
Hukum Boyle
Suhu tetap → PV = Konstan → P1V1 = P2V2
P, V, T Berubah (non adiabatis)
(P1V1) / (T1) = (P2V2) / (T2)
Adiabatis
P1V1 γ= P2V2γ
T1V1 γ − 1= T2V2γ − 1
γ = perbandingan kalor jenis gas pada tekanan tetap dan volum tetap → γ = Cp/Cv
Usaha
W = P(ΔV) → Isobaris
W = 0 → Isokhoris
W = nRT ln (V2 / V1) → Isotermis
W = − 3/2 nRΔT → Adiabatis ( gas monoatomik)
Keterangan:
T = suhu (Kelvin, jangan Celcius)
P = tekanan (Pa = N/m2)
V = volume (m3)
n = jumlah mol
1 liter = 10−3m3
1 atm = 105 Pa ( atau ikut soal!)
Jika tidak diketahui di soal ambil nilai ln 2 = 0,693
Mesin Carnot
η = ( 1 − Tr / Tt ) x 100 %
η = ( W / Q1 ) x 100%
W = Q1 − Q2
Keterangan :
η = efisiensi mesin Carnot (%)
Tr = suhu reservoir rendah (Kelvin)
Tt = suhu reservoir tinggi (Kelvin)
W = usaha (joule)
Q1 = kalor masuk / diserap reservoir tinggi (joule)
Q2 = kalor keluar / dibuang reservoir rendah (joule)
Hukum Termodinamika 2
“Hukum II termodinamika dalam menyatakan aliran kalor. Kalor mengalir secara spontan dari benda bersuhu tinggi ke benda bersuhu rendah dan tidak mengalir secara spontan dalam arah kebalikannya”
Hukum II termodinamika dalam pernyataan tentang mesin kalor
Tidak mungkin membuat suatu mesin kalor yang bekerja dalam suatu siklus yang semata-mata menyerap kalor dari sebuah reservoir dan mengubah seluruhnya menjadi usaha luar.
Hukum II termodinamika dalam pernyataan entropi (besaran termodinamika yang menyertai suatu perubahan setiap keadaan dari awal sampai akhir sistem dan menyatakan ketidakteraturan suatu sistem)
Total entropi semesta tidak berubah ketika proses reversibel terjadi dan bertambah ketia proses irreversible terjadi.
Rumus Termodinamika Lubang Hitam Entropi
Hukum kedua termodinamika mensyaratkan bahwa lubang hitam memiliki entropi. Jika lubang hitam tidak membawa entropi, akan memungkinkan untuk melanggar hukum kedua dengan melemparkan massa ke dalam lubang hitam.
Peningkatan entropi lubang hitam lebih banyak daripada mengkompensasi penurunan entropi yang dibawa oleh benda yang tertelan. Baca juga ? Lubang Hitam di Alam Semesta “Black Hole” dan Lubang Putih di Alam Semesta “White Hole”
Persamaan untuk entropi lubang hitam biasanya diberikan dengan rumus: Bekenstein-Hawking menduga bahwa entropi lubang hitam itu
yang diana dimana 




Fakta bahwa entropi lubang hitam juga merupakan entropi maksimal yang dapat diperoleh oleh Bekenstein yang terikat (dimana Bekenstein terikat menjadi persamaan) adalah pengamatan utama yang mengarah pada prinsip holografik (sebuah prinsip teori dawai dan properti yang seharusnya dimiliki gravitasi kuantum yang menyatakan bahwa deskripsi volume dari sebuah ruangdapat dianggap sebagai pengkodean pada batas dimensi yang lebih rendah ke wilayah itu—kemungkinan besar sebuah batas serupa-cahaya seperti horison gravitasi).
Kecepatan cahaya
Disimbolkan dengan c, adalah sebuah konstanta fisika universal yang penting dalam banyak bidang fisika. Nilai presisinya adalah 299.792.458 meter per detik (kira-kira 3,00×108 m/s)
Panjang Planck
Dalam fisika, Panjang Planck, dinotasikan ℓP, adalah satuan panjang, sama dengan 1,616199(97)×10−35 meter. Satuan ini adalah satuan dasar dalam sistem satuan Planck, dikembangkan oleh fisikawan Max Planck. Panjang Planck bisa didefinisikan dari 3 konstanta fisika dasar: kecepatan cahaya dalam vakum, konstanta Planck, dan konstanta gravitasi.
Panjang Planck ℓP didefinisikan dengan rumus
dengan 
Panjang Planck sekitar 10−20 kali diameter proton (partikel subatomik dengan muatan positif sebesar 1,6 × 10−19 coulomb dan massa 938 MeV (1,6726231 × 10−27 kg, atau sekitar 1.836 kali massa sebuah elektron).
Konstata gravitasi
Menurut hukum gravitasi universal, gaya tarik (F) antara dua benda proporsional terhadap massa benda (m1 dan m2), dan berbanding terbaik proporsional terhadap kuadrat jarak r, (hukum kuadrat terbalik) di antara keduanya:
G, adalah tetapan gravitasi.
Tetapan gravitasi sulit diukur secara akurat. Dalam SSI tahun 2010 direkomendasikan:
dengan standar ketidakpastan relative 1,2×10−4.
Koefisien aktivitas
Koefisien aktivitas adalah suatu faktor yang digunakan dalam termodinamika untuk memperhitungkan penyimpangan dari perilaku ideal dalam campuran zat kimia.
Dalam suatu campuran ideal, interaksi mikroskopis antara masing-masing pasangan spesi kimia adalah sama (atau secara makroskopik setara, perubahan entalpi larutan dan variasi volume dalam pencampuran adalah nol) dan, sebagai hasilnya, sifat-sifat campuran dapat diekspresikan secara langsung dalam bentuk konsentrasi sederhana atau tekanan parsial dari zat yang ada, misalnya hukum Raoult.
Deviasi dari idealitas diakomodasikan dengan memodifikasi konsentrasi dengan koefisien aktivitas. Secara analog, ekspresi yang melibatkan gas dapat disesuaikan untuk non-idealitas dengan menskala tekanan parsial dengan koefisien fugasitas (Fugasitas adalah besaran dari suatu tekanan ekuivalen yang dinyatakan dalam dimensi tekanan sebagai pengganti tekanan p menurut hukum gas ideal).
Konsep koefisien aktivitas terkait erat dengan aktivitas dalam kimia.
Definisi termodinamika
Potensial kimia, μB, dari suatu zat B dalam suatu campuran ideal cairan atau suatu larutan ideal dinyatakan oleh
di mana μoB adalah suatu potensial kimia dari suatu zat murni dan xB adalah fraksi mol zat dalam campuran.
Hal ini digeneralisasi untuk memasukkan perilaku non-ideal dengan menuliskan
di mana aB adalah aktivitas zat dalam campuran dengan
di mana γB adalah koefisien aktivitas, yang bergantung pada xB. Karena γB mendekati 1, zat tersebut berperilaku selayaknya ideal. Misalnya, jika γB ≈ 1, maka hukum Raoult adalah akurat. Untuk γB > 1 dan γB < 1, zat B menunjukkan penyimpangan positif dan negatif dari Hukum Raoult, berturut-turut. Suatu penyimpangan positif menyiratkan bahwa zat B lebih mudah menguap.
Dalam banyak kasus, karena xB menuju ke nol, koefisien aktivitas zat B mendekati konstan; hubungan ini merupakan Hukum Henry bagi pelarut. Hubungan ini saling terkait satu sama lain melalui persamaan Gibbs–Duhem. Perlu dicatat bahwa koefisien aktivitas umum adalah tidak berdimensi.
Secara detail: Hukum Raoult menyatakan bahwa tekanan parsial komponen B terkait dengan tekanan uap (tekanan saturasi) dan fraksi molnya xB dalam fasa cair,
dengan konvensi Dengan kata lain: Cairan murni mewakili kasus ideal.
Pada pengenceran tak terbatas, koefisien aktivitas mendekati nilai batas, γB∞. Dibandingkan dengan hukum Henry,
memberikan
Dengan kata lain: Senyawa ini menunjukkan perilaku nonideal dalam kasus encer.
Definisi di atas dari koefisien aktivitas tidak praktis jika senyawa tidak ada sebagai cairan murni. Ini sering terjadi untuk elektrolit atau senyawa biokimia. Dalam kasus seperti itu, definisi yang berbeda digunakan yang menganggap pengenceran tak terbatas sebagai keadaan ideal:
dengan dan
Simbol telah digunakan di sini untuk membedakan antara dua jenis koefisien aktivitas. Biasanya dihilangkan, karena jelas dari konteks yang dimaksudkan. Namun ada beberapa kasus di mana kedua jenis koefisien aktivitas diperlukan dan bahkan mungkin muncul dalam persamaan yang sama, misalnya, untuk larutan garam dalam campuran (air + alkohol). Ini terkadang merupakan sumber kesalahan.
Memodifikasi fraksi mol atau konsentrasi oleh koefisien aktivitas memberikan aktivitas efektif dari komponen, dan karenanya memungkinkan ekspresi seperti hukum Raoult dan konstanta kesetimbangan untuk diterapkan pada campuran ideal dan non-ideal.
Pengetahuan tentang koefisien aktivitas sangat penting dalam konteks elektrokimia karena perilaku larutan elektrolit sering jauh dari ideal, karena efek atmosfer ionik. Selain itu, mereka sangat penting dalam konteks kimia tanah karena volume rendah pelarut dan, akibatnya, konsentrasi elektrolit yang tinggi.
Dependensi pada parameter tetap
Turunan dari koefisien aktivitas sehubungan dengan suhu memiliki kaitan dengan entalpi molar berlebih oleh
Demikian pula, turunan dari koefisien aktivitas sehubungan dengan tekanan dapat dikaitkan dengan kelebihan volume molar.
Contoh Soal Termodinamika Entropi
1. Sejumlah gas dalam sebuah wadah mengalami pemuaian adiabatik. Berapakah perubahan entropi gas tersebut?
Pembahasan:
Selama proses adiabatik, tidak ada kalor yang masuk atau keluar sistem (gas). Karena Q = 0 maka ΔS = 0. Entropi sistem tidak berubah alias konstan. Bagaimana dengan penekanan adiabatik ? Pada dasarnya sama saja. Selama penekanan adiabatik, tidak ada kalor yang masuk atau keluar dari sistem (Q = 0). Karenanya entropi sistem konstan.
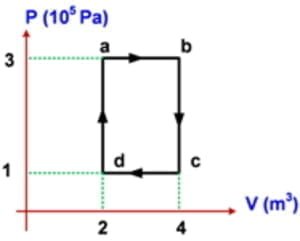
2. Suatu gas ideal mengalami proses siklus seperti pada gambar P − V. Kerja yang dihasilkan pada proses siklus ini adalah… kilojoule.
A. 200
B. 400
C. 600
D. 800
E. 1000
Pembahasan:
W = Usaha (kerja) = Luas kurva siklus = Luas bidang abcda
W = ab x bc
W = 2 x (2 x 105) = 400 kilojoule.
3. 1,5 m3 gas helium yang bersuhu 27oC dipanaskan secara isobarik sampai 87oC. Jika tekanan gas helium 2 x 105 N/m2 , gas helium melakukan usaha luar sebesar…
A. 60 kJ
B. 120 kJ
C. 280 kJ
D. 480 kJ
E. 660 kJ
Pembahasan:
Data:
V1 = 1,5 m3
T1 = 27oC = 300 K
T2 = 87oC = 360 K
P = 2 x 105 N/m2
W = PΔV
Mencari V2 :
V2/T2 = V1/T1
V2 = ( V1/T1 ) x T2 = ( 1,5/300 ) x 360 = 1,8 m3
W = PΔV = 2 x 105(1,8 − 1,5) = 0,6 x 105 = 60 x 103 = 60 kJ.
4. Suatu gas memiliki volume awal 2,0 m3 dipanaskan dengan kondisi isobaris hingga volume akhirnya menjadi 4,5 m3. Jika tekanan gas adalah 2 atm, tentukan usaha luar gas tersebut!
(1 atm = 1,01 x 105 Pa)
Pembahasan:
Data:
V2 = 4,5 m3
V1 = 2,0 m3
P = 2 atm = 2,02 x 105 Pa
Isobaris → Tekanan Tetap
W = P (ΔV)
W = P(V2 − V1)
W = 2,02 x 105 (4,5 − 2,0) = 5,05 x 105 joule.
5. 2000/693 mol gas helium pada suhu tetap 27oC mengalami perubahan volume dari 2,5 liter menjadi 5 liter. Jika R = 8,314 J/mol K dan ln 2 = 0,693 tentukan usaha yang dilakukan gas helium!
Pembahasan:
Data:
n = 2000/693 mol
V2 = 5 L
V1 = 2,5 L
T = 27oC = 300 K
Usaha yang dilakukan gas :
W = nRT ln (V2 / V1)
W = (2000/693 mol) ( 8,314 J/mol K)(300 K) ln ( 5 L / 2,5 L )
W = (2000/693) (8,314) (300) (0,693) = 4988,4 joule.
6. Mesin Carnot bekerja pada suhu tinggi 600 K, untuk menghasilkan kerja mekanik. Jika mesin menyerap kalor 600 J dengan suhu rendah 400 K, maka usaha yang dihasilkan adalah…
A. 120 J
B. 124 J
C. 135 J
D. 148 J
E. 200 J
Pembahasan:
Data:
η = ( 1 − Tr / Tt ) x 100 %
Hilangkan saja 100% untuk memudahkan perhitungan :
η = ( 1 − 400/600) = 1/3
η = ( W / Q1 )
1/3 = W/600
W = 200 J.
7. Suatu mesin Carnot, jika reservoir panasnya bersuhu 400 K akan mempunyai efisiensi 40%. Jika reservoir panasnya bersuhu 640 K, efisiensinya…%
A. 50,0
B. 52,5
C. 57,0
D. 62,5
E. 64,0
Pembahasan:
Data pertama:
η = 40% = 4 / 10
Tt = 400 K
Cari terlebih dahulu suhu rendahnya (Tr) hilangkan 100 % untuk mempermudah perhitungan:
η = 1 − (Tr/Tt)
4 / 10 = 1 − (Tr/400)
(Tr/400) = 6 / 10
Tr = 240 K
Pembahasan:
Data kedua:
Tt = 640 K
Tr = 240 K (dari hasil perhitungan pertama)
η = ( 1 − Tr/Tt) x 100%
η = ( 1 − 240/640) x 100%
η = ( 5 / 8 ) x 100% = 62,5%.
8. Jika kalor yang diserap reservoir suhu tinggi adalah 1200 joule, tentukan :
a) Efisiensi mesin Carnot
b) Usaha mesin Carnot
c) Perbandingan kalor yang dibuang di suhu rendah dengan usaha yang dilakukan mesin Carnot
d) Jenis proses ab, bc, cd dan da

a) Efisiensi mesin Carnot
Data :
Tt = 227oC = 500 K
Tr = 27oC = 300 K
η = ( 1 − Tr/Tt) x 100%
η = ( 1 − 300/500) x 100% = 40%
η = W/Q1
4/10 = W/1200
W = 480 joule
Q2 = Q1 − W = 1200 − 480 = 720 joule
Q2 : W = 720 : 480 = 9 : 6 = 3 : 2
d) Jenis proses ab, bc, cd dan da
ab → pemuaian isotermis (volume gas bertambah, suhu gas tetap)
bc → pemuaian adiabatis (volume gas bertambah, suhu gas turun)
cd → pemampatan isotermal (volume gas berkurang, suhu gas tetap)
da → pemampatan adiabatis (volume gas berkurang, suhu gas naik)
Aplikasi termodinamika yang biasa digunakan dalam kehidupan sehari-hari
1. Air Conditioner (AC)
Sistem kerja AC terdiri dari bagian yang berfungsi untuk menaikkan dan menurunkan tekanan supaya penguapan dan penyerapan panas dapat berlangsung. Kompresor yang ada pada sistem pendingin dipergunakan sebagai alat untuk memampatkan fluida kerja (refrigent), jadi refrigent yang masuk ke dalam kompresor dialirkan ke kondenser yang kemudian dimampatkan di kondenser.
2. Mesin penanak nasi (Rice Cooker)
Pada rice cooker, energi panas ini dihasilkan dari energi listrik. Suatu cairan akan menguap bila tekanan uap gas yang berasal dari cairan adalah sama dengan tekanan dari cairan ke sekitarnya (Puap = Pcair). Jadi, titik didih suatu cairan sebenarnya bisa dimanipulasi dengan meningkatkan tekanan di luar cairan (tekanan eksternal). Pada penanak nasi biasa, air akan dididihkan dengan tekanan eksternal biasa, yaitu 101 kPa, dan mendidih pada titik didih biasa, yaitu 100°C.
3. Dispenser air
Dispenser Prinsip kerja pemanas air Proses pemanasan air terjadi pada saat air masuk kedalam tabung pemanas.
Tabung pemanas merupakan tabung yang terbuat dari logam yang disekitar tabung tersebut dikelilingi oleh elemen pemanas:
Sehingga ketika air mengalir dari tampungan menuju tabung pemanas sensor suhu yang ada pada tabung pemanas akan memicu elemen pemanas untuk bekerja.
Suhu tinggi yang dihasilkan elemen pemanas diserap oleh air yang suhunya lebih rendah.
Setelah suhu air dalam tabung pemanas tinggi maksimal sensor suhu yang ada pada tabung pemanas akan memutuskan arus listrik pada elemen pemanas.
Pada saat elemen pemanas menyala lampu indikator pemanas menyala dan pada saat elemen pemanas mati lampu indikator pemanas mati.
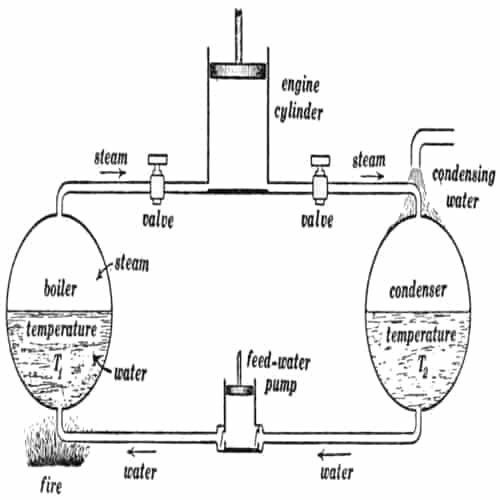
Sistem termodinamika
Sistem termodinamika adalah bagian dari jagat raya yang diperhitungkan. Sebuah batasan yang nyata atau imajinasi memisahkan sistem dengan jagat raya, yang disebut lingkungan.
Klasifikasi sistem termodinamika berdasarkan pada sifat batas sistem-lingkungan dan perpindahan materi, kalor dan entropi antara sistem dan lingkungan.
Terdapat 3 jenis sistem berdasarkan jenis pertukaran yang terjadi antara sistem dan lingkungan:
- Terisolasi: tak terjadi pertukaran panas, benda atau kerja dengan lingkungan. Contoh dari sistem terisolasi adalah wadah terisolasi, seperti tabung gas terisolasi.
- Tertutup: terjadi pertukaran energi (panas dan kerja) tetapi tidak terjadi pertukaran benda dengan lingkungan. Rumah hijau adalah contoh dari sistem tertutup di mana terjadi pertukaran panas tetapi tidak terjadi pertukaran kerja dengan lingkungan. Apakah suatu sistem terjadi pertukaran panas, kerja atau keduanya biasanya dipertimbangkanh sebagai sifat pembatasnya:
- pembatas adiabatik: tidak memperbolehkan pertukaran panas.
- pembatas rigid: tidak memperbolehkan pertukaran kerja.
- Terbuka: terjadi pertukaran energi (panas dan kerja) dan benda dengan lingkungannya. Sebuah pembatas memperbolehkan pertukaran benda disebut permeabel. Samudra merupakan contoh dari sistem terbuka.
Dalam kenyataan, sebuah sistem tidak dapat terisolasi sepenuhnya dari lingkungan, karena pasti ada terjadi sedikit pencampuran, meskipun hanya penerimaan sedikit penarikan gravitasi. Dalam analisis sistem terisolasi, energi yang masuk ke sistem sama dengan energi yang keluar dari sistem.
Hukum-hukum Dasar Termodinamika
Terdapat 4 Hukum Dasar yang berlaku di dalam sistem termodinamika, yaitu:
Hukum Awal (Zeroth Law) Termodinamika
- Hukum awal menyatakan bahwa dua sistem dalam keadaan setimbang dengan sistem ketiga, maka ketiganya dalam saling setimbang satu dengan lainnya. Hukum ini dimasukkan setelah hukum pertama.
Hukum pertama Termodinamika
- Hukum yang sama juga terkait dengan kasus kekekalan energi. Hukum ini menyatakan perubahan energi dalam dari suatu sistem termodinamika tertutup sama dengan total dari jumlah energi kalor yang disuplai ke dalam sistem dan kerja yang dilakukan terhadap sistem. Hukum ini dapat diuraikan menjadi beberapa proses, yaitu proses dengan Isokhorik, Isotermik, Isobarik, dan juga adiabatik.
- Hukum kedua termodinamika terkait dengan entropi. Tidak ada bunyi untuk hukum kedua termodinamika yang ada hanyalah pernyataan kenyataan eksperimental yang dikeluarkan oleh kelvin-plank dan clausius. Pernyataan clausius: tidak mungkin suatu sistem apapun bekerja sedemikian rupa sehingga hasil satu-satunya adalah perpindahan energi sebagai panas dari sistem dengan temperatur tertentu ke sistem dengan temperatur yang lebih tinggi.
Pernyataan kelvin-planck: tidak mungkin suatu sistem beroperasi dalam siklus termodinamika dan memberikan sejumlah netto kerja kesekeliling sambil menerima energi panas dari satu reservoir termal.(sumber Fundamentals of engineering thermodynamics (Moran J., Shapiro N.M. – 6th ed. – 2007 – Wiley) Bab5). “total entropi dari suatu sistem termodinamika terisolasi cenderung untuk meningkat seiring dengan meningkatnya waktu, mendekati nilai maksimumnya hal ini disebut dengan prinsip kenaikan entropi” merupakan korolari dari kedua pernyataan diatas (analisis Hukum kedua termodinamika untuk proses dengan menggunakan sifat entropi)(sumber Fundamentals of engineering thermodynamics (Moran J., Shapiro N.M. – 6th ed. – 2007 – Wiley) Bab6).
- Hukum kedua termodinamika terkait dengan entropi. Tidak ada bunyi untuk hukum kedua termodinamika yang ada hanyalah pernyataan kenyataan eksperimental yang dikeluarkan oleh kelvin-plank dan clausius. Pernyataan clausius: tidak mungkin suatu sistem apapun bekerja sedemikian rupa sehingga hasil satu-satunya adalah perpindahan energi sebagai panas dari sistem dengan temperatur tertentu ke sistem dengan temperatur yang lebih tinggi.
Hukum ketiga Termodinamika
- Hukum ketiga termodinamika terkait dengan temperatur nol absolut. Hukum ini menyatakan bahwa pada saat suatu sistem mencapai temperatur nol absolut, semua proses akan berhenti dan entropi sistem akan mendekati nilai minimum. Hukum ini juga menyatakan bahwa entropi benda berstruktur kristal sempurna pada temperatur nol absolut bernilai nol.
Contoh Soal dan Jawaban Termodinamika
1. Berikan penjelasan dan tuliskan komentar untuk pernyataan berikut ini: Sebuah silinder yang dilenmgkapi dengan piston berisi sejumlah gas. Di atas piston diletakkan 2 (dua) anak timbangan masing-masing dengan massa 1 kg, jika satu anak timbangan diambil maka tekanan dan volume sistem gas akan berubah.
Bagaimana pendapat Anda, contoh ini merupakan proses kuasistatik atau proses nonkuasistatik?
Jawaban:
Jelas sistem ini mengalami proses nonkuasistatik, sebab bukan merupakan rentetan keadaan setimbang tak terhingga banyak, melainkan hanya dua keadaan setimbang yaitu setimbang awal dan setimbang akhir.
2. Sebuah mesin Carnot yang menggunakan reservoir suhu tinggi sebesar 1000°K mempunyai efisiensi sebesar 50%. Agar efesiensinya naik menjadi 60%, berapakah reservoir suhu tinggi harus dinaikkan?
Jawab:
h = 1-T2/T1 —^ 0,5 = 1 T2/1000 jadi T2 = 500°K Apabila efesiensinya dijadikan 60% (dengan T2 tetap), maka h = 1 – T2/T1 —^ 0,6 =1 – 500/T2 jadi T1= 12.50 °K.
3. Berikan dan tuliskan penjelasan mengenai proses reversibel!
Jawab:
Proses reversibel adalah merupakan proses dari suatu keadaan awal ke keadaan tertentu dan dari keadaan akhir tersebut dimungkinkan terjadinya proses balik ke keadaan awal kembali melalui jalan yang sama. Sedemikian rupa dengan mudah jika pada sistem dikenai kondisi tertentu.
4. Tuliskan 2 (dua) persyaratan agar proses dikatakan berbalik (reversibel)
Jawab:
proses tersebut merupakan proses kuasistatik
dalam proses tersebut tidak terjadi efek-efek disipasi.
5. Berikan dan tuliskan penjelasan mengenai daur atau siklus.
Jawab:
Daur atau siklus adalah proses terus menerus yang merupakan sederetan proses yang terdiri atas beberapa tahapan dari suatu keadaan setimbang ke keadaan setimbang lain kemudian kembali keadaan setimbang semula yang hasilnya adalah pengubahan kalor menjadi kerja atau usaha luar.
6. Apakah pengubahan kalor seluruhnya menjadi usaha dapat terjadi?
Jawab:
Pengubahan kalor seluruhnya menjadi tenaga/usaha dalam satu tahap saja dapat terjadi; yaitu pada proses ekspansi isotermal sistem gas ideal.
– pelajari lebih lanjut, apakah proses yang demikian dapat diambil manfaatnya? (bacalah kembali uraian dengan seksama dan kembangkan wawasan dan penalaran Ada).
7. Selama proses isokhorik (v = 1 m3), gas menerima kalor 1000 kalori sehingga tekanan berubah sebesar 814 N/m2. Hitunglah perubahan energi dalam gas selama proses tersebut!
Jawab:
Proses isokhorik: AV = 0 sehingga AW = P . AV = 0 AQ = AU + AW ^ 1000 = AU + 0
Jadi perubahan energi dalam gas = 1000 kalori =1000 x 4.186 J = 4186J.
8. Gas diatomik pada suhu sedang 200°C dan tekanan 105 N/m2 bervolume 4 lt. Gas mengalami proses isobarik sehingga volumenya 6 liter kemudian proses isokhorik sehingga tekanannya 1.2 x 105 N/m2. Berapakah besar perubahan energi dalam gas selama proses tersebut?
Jawab:
PV = n R T—— ^ P AV + V AP = n R AT
Proses A – B (AP = 0):
P AV = n R AT = 105 . 2.10-3 = 200 J AUBC = 5/2 n R AT = 500 J (diatomik 200°C)
Proses :B – C (AV = 0):
V AP = n R AT = 6.10-3.0,2. 105 = 1120 J AUBC = 5/2 n R AT = 300 J (diatomik 200°C)
Jadi AU total = AUAB + AUBC = 800 J.
9. Mesin Carnot bekerja pada suhu tinggi 600 K, untuk menghasilkan kerja mekanik. Jika mesin menyerap kalor 600 J dengan suhu rendah 400 K, maka usaha yang dihasilkan adalah…
Jawab:
Diketahui:
T2 = 400 K
T1 = 600 K
Ditanyakan: Wdihasilkan?
Wdihasilkan = . Wserap = = 200 J
10. Bila suatu gas dimampatkan secara isotermik maka tentukanlah tekanan, energi dalam dan usaha yang dilakukan oleh gas!
Jawab:
Gas dimampatkan berarti volume gas bertambah kecil (AV < 0)
Proses gas secara isotermik berarti AT = 0 Jadi: PV = C——————— ^ P = C/V
Karena volume gas bertambah kecil maka tekanan gas akan bertambah besar. Kenaikan tekanan gas ini disebabkan oleh makin seringnya molekul-molekul gas menumbuk dinding tempatnya (jarak tempuh molekul gas makin pendek) bukan karena kecepatannya yang bertambah.
AU=3/2 n R AT
Karena proses isotermik (AT= 0), maka perubahan energi dalam sama dengan nol Berarti energi dalam gas tidak berubah.
AQ = AU + AW———– ^ AW = P AV
Karena AU = 0 maka AQ = AW, berarti kalor yang diserap gas seluruhnya diubah menjadi usaha gas. Karena volume gas bertambah kecil (DV < 0) maka usaha yang dilakukan gas negatif(AW < O), berarti gas menerima kerja dari luar.
11. Suatu gas memiliki volume awal 10 m3 dipanaskan dengan kondisi isobaris hingga volume akhirnya menjadi 25 m3. Jika tekanan gas adalah 2 atm, tentukan usaha luar gas tersebut! (1 atm = 1,01 x 105 Pa).
Jawab:
Diketahui:
V2 = 25 m3
V1 = 10 m3
P = 2 atm = 2,02 x 105 Pa
Ditanyakan: W?
Isobaris → Tekanan Tetap, gunakan rumus W = P (ΔV)
W = P(V2 − V1)
W = 2,02 x 105 x (25 − 10) = 3,03 x 106 joule.
12. 1,5 m3 gas helium yang bersuhu 27oC dipanaskan secara isobarik sampai 87oC. Jika tekanan gas helium 2 x 105 N/m2, gas helium melakukan usaha luar sebesar…
A. 60 kJ
B. 120 kJ
C. 280 kJ
D. 480 kJ
E. 660 kJ
Pembahasan
Data :
V1 = 1,5 m3
T1 = 27oC = 300 K
T2 = 87oC = 360 K
P = 2 x 105 N/m2
W = PΔV
Mencari V2 :
V2/T2 = V1/T1
V2 = ( V1/T1 ) x T2 = ( 1,5/300 ) x 360 = 1,8 m3
W = PΔV = 2 x 105(1,8 − 1,5) = 0,6 x 105 = 60 x 103 = 60 kJ.
13. Pernyataan yang benar tentang proses termodinamika adalah…
A. isobarik adalah proses perubahan gas pada tekanan tetap
B. isobarik adalah proses perubahan gas pada suhu tetap
C. isokhorik merupakan proses perubahan gas pada tekanan tetap
D. isotermis adalah proses perubahan gas pada volume tetap
E. isokhorik adalah proses perubahan gas pada suhu tetap
Pembahasan:
Isobarik = tekanan tetap
Isokhorik = volume tetap
Isotermis = suhu tetap
Jawaban yang benar adalah A.
14. Suatu gas memiliki volume awal 2 m3 dipanaskan dengan isobaris hingga volume akhirnya 4,5 m3. Jika tekanan gas adalah 2 atm, tentukan usaha luar gas tersebut (1 atm = 1,01 x 105 Pa)
Penyelesaian :
Dik : V1=2 m3
V2=4,5 m3
P = 2 atm = 2,02 x 105 Pa
Dit : W? isobaris = tekanan tetap
Jawab :
W = P (ΔV)
W = P ( V2 – V1)
W = 2,02 x 105 Pa . (4,5 – 2,0)
= 5,05 x 105 Joule
15. Berikan dan tuliskan penjelasan mengenai proses reversibel.
Jawab:
Proses reversibel adalah merupakan proses dari suatu keadaan awal ke keadaan tertentu dan dari keadaan akhir tersebut dimungkinkan terjadinya proses balik ke keadaan awal kembali melalui jalan yang sama. Sedemikian rupa dengan mudah jika pada sistem dikenai kondisi tertentu.
16. Suatu gas yang menghasilkan usaha sebesar 200 joule, dengan perubahan energy dalam pada ags adalah 70 J. Tentukanlah kalor yang dapat diterima gas tersebut!
Penjelasan dan jawaban:
Diketahui: W = 200 J
êU = 70 J
Ditanyakan: Q …?
Jawab:
êU = Q – w
Q = êU + W
Q = (70 + 200) J
Q = 270 J
17. Gas sebanyak dua liter dipanaskan dari suhu 47 derajat celcius sampai 127 derajat celcius pada tekanan 2×1052×105 N/m2. Usaha gas tersebut sebesar…
Jawab :
Diketahui :
Ditanya : Usaha WW = ….?.
Jawab:
Ini merupakan soal tentang termodinamika khususnya isobarik. Karena dari soal terlihat tekanannya dibuat tetap. Kita tahu rumus untuk mencari usaha pada keadaan isobarik -tekanan tetap – adalah :
Terlebih dahulu kita harus mencari nilai V2V2 dulu dengan memakai persamaan :
Berarti:
Jadi, usaha yang dilakukan oleh gas tersebut adalah :
18. Sejumlah 6 mMol gas hidrogen suhunya dinaikkan dari 20 oc menjadi 110 oc pada tekanan tetap. Jika konstanta gas umum R = 8,314J/mol.K, tentukan:
a) perubahan energy dalam
b) usaha yang dilakukan gas
c) kalor yang diperlukan
Penjelasan dan jawaban:
diketahui: n = 6 mMol =0,006 mol
T1 = 20 oc (20 + 273) K = 293 K
T2 = 110 oc (110 + 273)K = 383 K
R = 8,314 J/mol.K
Ditanyakan: a) êU …?
- b) W …?
- c) Q …?
Jawab:
a). êU = 3/2nR(T2 –T1)
= 3/2 (0,006 . 8,314 (383 – 293)) J
= 3/2 (4,489) J
= 6,734 J
b). W = P (V2 – V1) P = nR
V1 = T1
V2 = T2
W = nR (T2 – T1)
W = o,oo6 x 8,314 (383 – 293)
W = 4,489 J
c). Q = êU + W
Q = (6,734 + 4,489) J = 2,245 J
19. Gas helium M = 4 g/mol sebanyak 8 gram mengalami ekspansi isotermik dari 2 liter menjadi 4 liter pada suhu 47 derajat celcius. Tentukan usaha yang dilakukan oleh gas helium!. ln 2 = 0,693
Jawab:
Diketahui :
M = 4 g/mol
Massa m = 8 g
Volume awal v1=2v1=2 liter =2.10−3m32.10−3m3
Volume akhir v2=4v2=4 liter=4.10−3m34.10−3m3
Suhu T = 47 Celcius = 273 + 47 = 320 K
R = 8.314 J/kmol.K
Ditanya : W = …?.
Jawab:
Soal ini merupakan soal tentang termodinamika dalam kondisi isotermik. Usaha yang dilakukan oleh gas dalam kondisi isotermik secara matematis dirumuskan dengan:
Dan didalam soal belum terlihat adanya nilai mol nn, kita tahu untuk mencari nilai mol kita memakai rumus:
20. Suatu gas menerima kalor 1.500 kalori, menghasilkan usaha sebesar 4.000 J. Berapakah energy dalam pada gas? (1 kalori = 4,18 joule)
Penjelasan dan jawaban:
Diketahui: Q = 1.500 kalori (1 kalori = 4,18 joule)
Q = 1.500 x 4,18 J = 6.720 J
W = 4.000 J
Ditanyakan: êU …?
Jawab:
êU = êQ – W
êU = (6.200 – 4.000) J
êU = 2.270 J.
21. Gas helium 0,0003 mol pada tekanan tetap. Suhunya dinaikkan dari 10 oc menjadi 70 oc. diketahui R = 8,314 J/mol.K, hitunglah kalor yang diperlukan?
Penjelasan dan jawaban:
Diketahui: n = 0,0003 mol
T1 = 10 oc = (10 + 273) K = 283 K
T2 = 70 oc =(70 + 273)
R = 8,314 J/mol.K
Ditanyakan: Q ….?
Jawab:
Q = êU + W êU = 3/2nR (T2 – T1)
W = P (V2 – V1) = nR(T2 – T1)
êU = 3/2nR (T2 – T1)
êU = 3/2(0,0003 x 8,314 (343 – 283))
êU = 3/2 (0,149) J
êU = 0,224 J
W = nR(T2 – T1)
W = 0,0003 x 8,314 (343 – 283)
W = 0,149 J
Jadi, kalor yang diperlukan:
Q = êU + W
Q = (0,224 + 0,149) J
Q = 0,373 J
22. Suatu zat menerima kalor 20 kalori, suhunya dinaikkan dari 15 oc menjadi 50 oc. Tentukan kapasitas kalor yang diperlukan untu menaikkan suhu zat tersebut! (1 kalori = 4,18 joule)
Penjelasan dan jawaban:
Diketahui: Q = 20 kalor (1 kalor = 4,18 J)
Jadi, Q = 20 x 4,18 J =83,6 J
T1 = 15 oc = (15 + 273) K = 288 K
T2 = 50 oc = (50 + 273) K = 323 K
Ditanyakan: C ….?
Jawab:
C = QêT êT = T2 –T1
êT = (323 – 288) K = 35 K
C = 83,6 J/35 K
C = 2,389 J/K
23. Sejumlah 0,005 mol gas hydrogen suhunya dinaikkan 12 oc menjadi 64 oc pada tekanan tetap. Jika konstanta gas umum R = 8,314 J/mol.K, tentukan:
a) perubahan energy dalam
b) kapasitas kalor pada tekanan tetap
c) kapasiras kalor pada volume tetap
penyelesaian:
diketahui: n = 0,005 mol
T1 = 12 oc = (12 + 273) K = 285 K
T2 = 64 oc = (64 + 273) K = 337 K
R = 8,314 J/mol.K
Ditanyakan: a). êU …?
b). Cp …?
c). Cv …?
Jawab:
a). êU = 3/2 nRêT
êU = 3/2 (0,005 x 8,314 (337 – 285))
êU = 3/2 (3,162) J
êU = 3,243 J
b). Cp = 3/2 nR
Cp = 3/2 (0,005 x 8,314)
Cp = 3/2 (0,042)
Cp = 0,063 J/K
c). Cv = 5/2 nR
Cv = 5/2 (0,005 x 8,314)
Cv = 5/2(0,042)
Cv = 0,105 J/K.
24. Gas diatomik dipanaskan pada volume tetap dengan kapasitas kalor 24 J/K. jika R = 8,314 J/mol.K, tentukan jumlah mol gas tersebut!
Penjelasan dan jawaban:
Diketahui:
Cv = 24 J/k
R = 8,314 J/mo.K
Ditanyakan: n ….?
Jawab:
Cv = 3/2 nR
24 J/K = 3/2 n x8,314 J/mol.K
24 = 12,471 x n
n = 24/12,471 mol
n = 1,924 mol.
25. Sejumlah 3 mol gas monoatomik pada tekanan tetap. Jika R = 8,314 J/mol.K, tentukan kapasits kalor pada tekanan tetap untuk gas momoatomik tersebut!
Penjelasan dan jawaban:
Diketahui: n = 3 mol
R = 8,314 J/mol.K
Ditanyakan: Cp …?
Jawab:
Cp = 5/2 nR
Cp = 5/2 (3 x 8,314)
Cp = 5/2 (29,942)
Cp = 62,355 J/K.
26. Gas diatomik dipanaskan pada keadaan tetap dengan kapasitas kalor 520 J/K. diketahui konstanta gas umum R = 8,314 J/mol.K, tentukan:
a) jumlah mol gas (kapasitas kalor pada volume tetap)
b) jumlah mol gas (kapasitas kalor pada tekanan tetap)
Penjelasan dan jawaban:
Diketahui: C = 520 J/K
R = 8,314 J/mol.K
Ditanyakan:
a) nv …?
b) np …?
Jawab:
a) Cv = 5/2 nR
520 J/K = 5/2n x 8,314 J/mol.k
520 = 20,785 x n
nv = 520/20,785 mol
nv = 25,018 mol
b) Cv = 7/2 nR
520 J/K = 7/2n x 8,314 J/mol.k
520 = 29,099 x n
np = 520/29,099 mol
np = 17,870 mol
Bacaan Lainnya
- Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
- Senyawa Organik – Rumus Kimia, Soal dan Jawaban
- Rumus Kimia Konsep Mol Dan Empiris Beserta Contoh Soal Dan Jawaban
- Sebagian cabang biologi: Biofisika
- Contoh Soal SBMPTN Beserta Jawabannya
- Tabel Periodik Lengkap Dengan Daftar Unsur Kimia Berdasarkan Nama, Warna Dan Jenis
- Pemahaman Kanker: Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Apakah Produk Pembalut Wanita Aman?
- Penyakit Difteri Penularan, Penyebab, Gejala, Perawatan dan Pencegahan
- Penyakit Kusta Penularan, Penyebab, Gejala, Perawatan dan Pencegahan
- Sakit Punggung: Penyebab, gejala, pencegahan dan perawatan
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing


















