Penjelasan Persamaan Nilai absolut atau nilai mutlak atau modulus

Nilai absolut atau nilai mutlak adalah nilai suatu bilangan riil tanpa tanda plus atau minus. Baik $|a|$ ataupun $|-a|$ sama-sama bernilai $a$ . Sebagai contoh, nilai absolut dari 3 adalah 3, dan nilai absolut dari –3 juga 3.

Untuk semua bilangan riil a nilai absolut dinyatakan dengan $| a |$ (a diapit garis vertikal) dan didefinisikan sebagai:

|a|={\begin{cases}a,&{\mbox{jika }}a\geq 0\\-a,&{\mbox{jika }}a<0.\end{cases}}

Persamaan Nilai Mutlak adalah

Suatu nilai mutlak dari sebuah bilangan yang dapat didefinisikan sebagai jarak bilangan tersebut terhadap titik 0 pada garis bilangan tanpa memperhatikan arahnya.

Dari definisi di atas, nilai absolut a akan selalu positif atau nol, tetapi tidak pernah negatif

Definisi lain dari nilai absolut adalah

|a|={\sqrt {a^{2}}}

|a|^{2}=a^{2}\,

karena nilai dari akar kuadrat diwakili bilangan positif.

Definisi ini sering digunakan untuk menyelesaikan suatu persamaan absolut. Contoh:

|x-2|=x

|x-2|^{2}=x^{2}

(x-2-x^{2})(x-2+x^{2})=0

(x^{2}-x+2)(x^{2}+x-2)=0

x=1\lor x=-2

(Catatan: $x^{2}-x+2$ tidak mempunyai akar riil.)

Dalam bentuk persamaan mutlak sebagai berikut:

|f(x)|=g(x)

haruslah mempunyai dua nilai yaitu

|f(x)|=\left\{{\begin{matrix}f(x),&{\mbox{maka penyelesaian}}f(x)\geq 0\\\\-f(x),&{\mbox{maka penyelesaian}}f(x)<0\end{matrix}}\right.

Persamaan mutlak akan memungkinkan definit + dan – karena tidak memotong dan menyinggung sumbu y.

Contoh Soal Persamaan Nilai Mutlak atau Nilai Absolut beserta jawabannya

1. Tentukanlah himpunan penyelesaian dari persamaan |4 – 2/5 x|-7 = 13

Jawab :

|4 – 2/5 x|-7 = 13
|4 – 2/5 x|= 13 + 7
|4 – 2/5 x|= 20

maka

|4 – 2/5 x|= 20 atau |4 – 2/5 x|= -20

sehingga

– 2/5 x = 16 atau -2/5 x = -24
x = -40 atau x = 60

Maka himpunan penyelesaiannya adalah {-40,60}

2. Tentukan nilai x dari persamaan $|x^{2}+x|=12$ !

|x^{2}+x|=12

batasan f(x): $x^{2}+x=12$; $x^{2}+x-12=0$; $(x+4)(x-3)=0$; $x=-4\lor x=3$

batasan -f(x): $x^{2}+x=-12$; $x^{2}+x+12=0$ definit +

HP=\{x|x=\{-4,3\},x\in R\}

3. Tentukan nilai x dari persamaan $|{\sqrt {x^{2}-4x}}|=|{\sqrt {3x-10}}|$ !

|{\sqrt {x^{2}-4x}}|=|{\sqrt {3x-10}}|

({\sqrt {x^{2}-4x}})^{2}=({\sqrt {3x-10}})^{2}

x^{2}-4x=3x-10

x^{2}-7x+10=0

(x-2)(x-5)=0

x=2\lor x=5

HP=\{x|x=\{2,5\},x\in R\}

4. Tentukanlah sebuah himpunan penyelesaian dari |3x – 7| = 3

Penyelesaian :
Berdasarkan sifat a :
|3x – 7| = 3 ⇔ 3x – 7 = 3 atau 3x – 7 = -3
|3x – 7| = 3 ⇔ 3x = 10 atau 3x = 4
|3x – 7| = 3 ⇔ x = 5 atau x = 3

Maka, HP = {3, 5}.

5. Tentukan nilai x dari |3x+2|²+|3x+2|-2=0

Penyelesaian :

Misal : |3x+2| = p

maka

|3x+2|²+|3x+2|-2=0

p² + p – 2 = 0

(p+2) (p-1) = 0

p+2 = 0

p = -2 (nilai mutlak tidak negatif )

atau

p-1 = 0

p = 1

|3x+2| = 1

=> 3x+2 = 1

3x = 1-2

3x = -1

x = -1/3

=> -(3x+2) = 1

3x+2 = -1

3x = -1-2

3x = -3

x = -1

Jadi penyelesaiannya adalah x=-1/3 atau x=-1

6. Tentukan nilai x dari persamaan $|x^{2}-4x-12|-|7-6x|=5$ !

terlebih dahulu untuk mempunyai batas-batas yang ada

untuk | x^2 – 4x – 12 |: $|x^{2}-4x-12|=\left\{{\begin{matrix}x^{2}-4x-12,&{\mbox{maka penyelesaian}}x^{2}-4x-12\geq 0\\\\-(x^{2}-4x-12),&{\mbox{maka penyelesaian}}x^{2}-4x-12<0\end{matrix}}\right.$

batasan f(x): $x^{2}-4x-12\geq 0$

dibuat harga nol

x^{2}-4x-12=0

(x+2)(x-6)=0

x=-2\lor x=6

dibuat irisan

	-2		6
+++	N/A	—-	N/A	+++

x\leq -2\lor x\geq 6

batasan -f(x): $x^{2}-4x-12<0$

dibuat harga nol

x^{2}-4x-12=0

(x+2)(x-6)=0

x=-2\lor x=6

dibuat irisan

	-2		6
+++	N/A	—-	N/A	+++

-2<x<6

untuk | 7 – 6x |: $|7-6x|=\left\{{\begin{matrix}7-6x,&{\mbox{maka penyelesaian}}7-6x\geq 0\\\\-(7-6x),&{\mbox{maka penyelesaian}}7-6x<0\end{matrix}}\right.$

batasan f(x): $7-6x\geq 0$; $x\leq {\frac {7}{6}}$

batasan -f(x): $7-6x<0$; $x>{\frac {7}{6}}$

keempat batas-batas akan dibuat irisan

irisan		-2		7/6		6
pertama	x^2 – 4x – 12	N/A		N/A		N/A	x^2 – 4x – 12
kedua		N/A	-(x^2 – 4x – 12)	N/A	-(x^2 – 4x – 12)	N/A
ketiga	7 – 6x	N/A	7 – 6x	N/A		N/A
keempat		N/A		N/A	-(7 – 6x)	N/A	-(7 – 6x)

untuk x <= -2

x^{2}-4x-12-(7-6x)=5

x^{2}-4x-12-7+6x-5=0

x^{2}+2x-24=0

(x+6)(x-4)=0

x=-6\lor x=4

x=-6

dipenuhi

untuk -2 < x <= 7/6

-(x^{2}-4x-12)-(7-6x)=5

-x^{2}+4x+12-7+6x-5=0

x^{2}-10x=0

x(x-10)=0

x=0\lor x=10

hanya

x=0

dipenuhi

untuk 7/6 < x < 6

-(x^{2}-4x-12)-(-(7-6x))=5

-x^{2}+4x+12+7-6x-5=0

x^{2}+2x=0

x(x+2)=0

x=0\lor x=-2

tidak memenuhi

untuk x >= 6

x^{2}-4x-12-(-(7-6x))=5

x^{2}-4x-12+7-6x-5=0

x^{2}-10x-10=0

definit +

tidak memenuhi

HP=\{x|x=\{-6,0\},x\in R\}

7. Tentukanlah himpunan dari |3x – 1| = |x + 4|

Penyelesaian :
Berdasarkan sifat a :
|3x – 1| = |x + 4|
⇔ 3x – 1 = x + 4 atau 3x – 1 = -(x + 4)
⇔ x = 5 atau 4x = -4
⇔ x = 5 atau x = -1

Maka, HP = {-1, 5}.

8. Selesaikanlah persamaan -3|x-4|+5 = 14

Jawab :

Isolasikan nilai mutlak dengan cara memisahkan nilai mutlak agar berada pada satu ruas, sementara suku yang lain akan kita pindahkan menuju ruas yang lain.

-3|x-4|+5 = 14
-3|x-4|= 14 – 5
-3|x-4|= 9
|x-4|= 3

Pada persamaan nilai mutlak x-4 adalah “X” sehingga kita bisa menyimpulkan bahwa:

x-4 = 3 atau x-4 = -3

sehingga

x = 7 atau x = 1

maka himpunan penyelesaian dari persamaan di atas adalah {7,1}

9. Tentukan nilai x yang memenuhi |2x+16|=x+4

Penyelesaian :

|2x+16|

===> 2x+16 untuk 2x+16 ≥ 0

2x ≥ -16

x ≥ -16/2

x ≥ -8

===> -(2x+16) untuk 2x+16 < 0

2x < -16

x < -16/2

x < -8

====>Untuk interval x≥-8

|2x+16| = x+4

2x+16 = x+4

2x-x = 4-16

x = -12

x=-12 tidak termuat dalam interval x≥8

Jadi interval x≥8 tidak mempunyai penyelesaian.

====>Untuk interval x<-8

|2x+16| = x+4

-(2x+16) = x+4

-2x-16 = x+4

-2x-x = 4+16

-3x = 20

x = 20/-3

x = -6 2/3

x=-6 2/3 tidak termuat dalam interval x<-8

Jadi interval x<-8 tidak mempunyai penyelesaian.

10. Tentukanlah himpunan penyelesaian |4x + 2| ≥ 6

Jawaban :
|4x + 2| ≥ 6 (4x + 2 ≤ -6 atau 4x + 2 ≥ 6)
|4x + 2| ≥ 6 (4x ≤ -8 atau 4x ≥ 4)
|4x + 2| ≥ 6 (x ≤ -2 atau x ≥ 1)

Maka, HP = (x ≤ -2 atau x ≥ 1)

11. Tentukan penyelesaian dari |x-2| = |6+2x|

Penyelesaian :

|x-2| = |6+2x|

(x-2)² = (6+2x)²

x²-4x+4 = 36+24x+4x²

0 = 4x²-x²+24x+4x+36-4

0 = 3x²+28x+32

0 = (3x+4) (x+8)

3x+4 = 0

3x = -4

x = -4/3

atau

x+8 = 0

x = -8

Sehingga penyelesaiannya x=-4/3 atau x=-8

12. Tentukan nilai x dari persamaan $|{\frac {x+4}{10-x}}|=|{\frac {1}{x-2}}|$ !

|{\frac {x+4}{10-x}}|=|{\frac {1}{x-2}}|

({\frac {x+4}{10-x}})^{2}=({\frac {1}{x-2}})^{2}

({\frac {x+4}{10-x}})^{2}-({\frac {1}{x-2}})^{2}=0

({\frac {x+4}{10-x}}+{\frac {1}{x-2}})({\frac {x+4}{10-x}}-{\frac {1}{x-2}})=0

({\frac {(x+4)(x-2)+10-x}{(10-x)(x-2)}})({\frac {(x+4)(x-2)-(10-x)}{(10-x)(x-2)}})=0

({\frac {x^{2}+2x-8+10-x}{(10-x)(x-2)}})({\frac {x^{2}+2x-8-10+x}{(10-x)(x-2)}})=0

({\frac {x^{2}+x+2}{(10-x)(x-2)}})({\frac {x^{2}+3x-18}{(10-x)(x-2)}})=0

akar dari ${\frac {x^{2}+x+2}{(10-x)(x-2)}}$: ${\frac {x^{2}+x+2}{(10-x)(x-2)}}=0$; $x^{2}+x+2=0$ definit +

{\frac {x^{2}+3x-18}{(10-x)(x-2)}}

{\frac {x^{2}+3x-18}{(10-x)(x-2)}}=0

x^{2}+3x-18=0

(x+6)(x-3)=0

x=-6\lor x=3

HP=\{x|x=\{-6,3\},x\in R\}

Penjelasan Pertidaksamaan Mutlak

Pertidaksamaan nilai mutlak merupakan jenis pertidaksamaan yang mengandungnilai mutlak. Nilai mutlak menghitung jarak suatu angka dari 0—misal, x. mengukur jarak x dari nol.

Dalam bentuk pertidaksamaan mutlak sebagai berikut:

|f(x)|<g(x)

atau

|f(x)|>g(x)

haruslah mempunyai dua nilai yaitu

|f(x)|=\left\{{\begin{matrix}|f(x)|<g(x),&{\mbox{maka penyelesaian}}-g(x)<f(x)<g(x)\\\\|f(x)|>g(x),&{\mbox{maka penyelesaian}}f(x)<-g(x)\lor f(x)>g(x)\end{matrix}}\right.

Pertidaksamaan mutlak akan memungkinkan definit + dan – karena tidak memotong dan menyinggung sumbu y.

Langkah-langkah Menyelesaikan Pertidaksamaan Nilai Mutlak

Pertidaksamaan nilai mutlak merupakan jenis pertidaksamaan yang mengandung nilai mutlak didalamnya. Nilai mutlak menghitung jarak pada suatu angka dari 0—misal, |x| mengukur jarak x dari nol.

Pertidaksamaan nilai mutlak bisa didapatkan dan di terapkan dalam simetri, batas-batas simetris, ataupun kondisi batas. Pahami dan selesaikanlah jenis-jenis pertidaksamaan ini dengan beberapa langkah yang sederhana, baik dengan cara evaluasi ataupun transformasi.

Langkah 1
Evaluasi bentuk pertidaksamaan nilai mutlak. Seperti yang sudah disebutkan di atas, nilai mutlak x, yang dinotasikan dengan |x|, didefinisikan sebagai berikut ini :

Pertidaksamaan nilai mutlak umumnya mempunyai salah 1 bentuk berikut :

|x| < a atau |x|> a ; |x±a| < b atau |x±a| > b ; |ax2+bx| < c

Pada artikel ini, fokusnya adalah pertidaksamaan dengan bentuk |f(x)|< a maupun |f(x)| > a , dengan f(x) berupa fungsi apapun dan a adalah kosntanta.

Langkah 2
mengubah dahulu pertidaksamaan nilai mutlak hingga menjadi pertidaksamaan biasa. Ingat bahwa nilai mutlak dari x bisa bernilai x positif maupun x negatif. Pertidaksamaan nilai mutlak |x| < 3 juga bisa diubah jadi 2 pertidaksamaan: -x < 3 dan x < 3.

Contoh :

│x−3│>5 bisa dirubah menjadi – (x-3) > 5 atau x-3 > 5.
|3x+2| < 5 bisa dirubah menjadi – (3x+2) < 5 atau 3x+2 < 5.
Istilah “atau” diatas memiliki arti bahwa kedua pertidaksamaan itu memenuhi persyaratan soal nilai mutlak.

Langkah 3
Kita abaikan saja tanda pertidaksamaan ketika mencari nilai x untuk persamaan yang pertama. Jika membantu, ubah saja tanda pertidaksamaan menjadi tanda sama dengan hingga bagian akhir hanya untuk sementara.

Langkah 4
Cari nilai x seperti yang biasa di lakukan. Ingat bahwa jika membagi dengan angka negatif untuk menyendirikan x ke salah 1 sisi dari tanda pertidaksamaan, harus membalik tanda pertidaksamaannya.

Contohnya, jika membagi kedua sisi dengan -1, -x > 5 bisa menjadi x < -5.

Langkah 5
Tulis himpunan penyelesaiannya. Dari nilai diatas, perlu menulis jangkauan nilai yang bisa disubstitusikan ke x. Jangkauan nilai ini sering juga dikenal sebagai himpunan penyelesaian.

Karena harus menyelesaikan dua pertidaksamaan dari pertidaksamaan nilai mutlak tersebut, maka akan mempunyai 2 penyelesaian.

Pada contoh yang dipakai di atas, penyelesaiannya bisa ditulis dengan 2 cara yakni :

-7/3 < x < 1
(-7/3,1)

Contoh Soal dan Jawaban Pertidaksamaan Nilai mutlak

1. Tentukan nilai x dari persamaan $|x^{2}-4x-12|-|7-6x|\geq 5$ !

terlebih dahulu untuk mempunyai batas-batas yang ada

untuk | x^2 – 4x – 12 |: $|x^{2}-4x-12|=\left\{{\begin{matrix}x^{2}-4x-12,&{\mbox{maka penyelesaian}}x^{2}-4x-12\geq 0\\\\-(x^{2}-4x-12),&{\mbox{maka penyelesaian}}x^{2}-4x-12<0\end{matrix}}\right.$

batasan f(x): $x^{2}-4x-12\geq 0$

dibuat harga nol

x^{2}-4x-12=0

(x+2)(x-6)=0

x=-2\lor x=6

dibuat irisan

	-2		6
+++	N/A	—-	N/A	+++

x\leq -2\lor x\geq 6

batasan -f(x): $x^{2}-4x-12<0$

dibuat harga nol

x^{2}-4x-12=0

(x+2)(x-6)=0

x=-2\lor x=6

dibuat irisan

	-2		6
+++	N/A	—-	N/A	+++

-2<x<6

untuk | 7 – 6x |: $|7-6x|=\left\{{\begin{matrix}7-6x,&{\mbox{maka penyelesaian}}7-6x\geq 0\\\\-(7-6x),&{\mbox{maka penyelesaian}}7-6x<0\end{matrix}}\right.$

batasan f(x): $7-6x\geq 0$; $x\leq {\frac {7}{6}}$

batasan -f(x): $7-6x<0$; $x>{\frac {7}{6}}$

keempat batas-batas akan dibuat irisan

irisan		-2		7/6		6
pertama	x^2 – 4x – 12	N/A		N/A		N/A	x^2 – 4x – 12
kedua		N/A	-(x^2 – 4x – 12)	N/A	-(x^2 – 4x – 12)	N/A
ketiga	7 – 6x	N/A	7 – 6x	N/A		N/A
keempat		N/A		N/A	-(7 – 6x)	N/A	-(7 – 6x)

untuk x <= -2

x^{2}-4x-12-(7-6x)\geq 5

x^{2}-4x-12-7+6x-5\geq 0

x^{2}+2x-24\geq 0

dibuat harga nol

x^{2}+2x-24=0

(x+6)(x-4)=0

x=-6\lor x=4

dibuat irisan

	(-6)		(-2)		(4)
Ya	N/A	Ya	N/A	Tidak	N/A	Tidak
+++	N/A	—-	N/A	—-	N/A	+++

x\leq -6

untuk -2 < x <= 7/6

-(x^{2}-4x-12)-(7-6x)\geq 5

-x^{2}+4x+12-7+6x-5\geq 0

x^{2}-10x\leq 0

dibuat harga nol

x^{2}-10x=0

x(x-10)=0

x=0\lor x=10

dibuat irisan

	-2		(0)		(7/6)		(10)
Tidak	N/A	Ya	N/A	Ya	N/A	Tidak	N/A	Tidak
+++	N/A	+++	N/A	—-	N/A	—-	N/A	+++

0\leq x\leq {\frac {7}{6}}

untuk 7/6 < x < 6

-(x^{2}-4x-12)-(-(7-6x))\geq 5

-x^{2}+4x+12+7-6x-5\geq 0

x^{2}+2x\leq 0

dibuat harga nol

x^{2}+2x=0

x(x+2)=0

x=0\lor x=-2

dibuat irisan

	(-2)		(0)		7/6		6
Tidak	N/A	Tidak	N/A	Tidak	N/A	Ya	N/A	Tidak
+++	N/A	—-	N/A	+++	N/A	+++	N/A	+++

\varnothing

untuk x >= 6

x^{2}-4x-12-(-(7-6x))\geq 5

x^{2}-4x-12+7-6x-5\geq 0

x^{2}-10x-10\geq 0

definit +

\varnothing

HP=\{x|x\leq -6\lor 0\leq x\leq {\frac {7}{6}},x\in R\}

gabungkan ketiga batas-batas. jadi:

HP=\{x|-{\frac {11}{5}}\leq x<-{\frac {4}{3}}\lor -{\frac {4}{3}}\leq x\leq 3,x\in R\}

HP=\{x|-{\frac {11}{5}}\leq x\leq 3,x\in R\}

Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) │x – 6│ ≤ 9
(b) │x + 2│ > 4

Jawaban:
(a) │x – 6│ ≤ 9
–9 ≤ x – 6 ≤ 9
–9 + 6 ≤ x – 6 + 6 ≤ 9 + 6
–3 ≤ x ≤ 15
(b) │x + 2│ > 4
x + 2 < –4 atau x + 2 > 4
x < –4 – 2 atau x > 4 – 2
x < –6 atau x > 2

02. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) │2x + 1│ ≥ │x – 2│
(b) │x + 2│ > 2│x – 1│

Jawaban:
(a) │2x + 1│ ≥ │x – 2│

(2x + 1)2 ≥ (x – 2)²
4x² + 4x + 1 ≥ x² – 4x + 4
3x² + 8x – 3 ≥ 0
(3x – 1)(x + 3) ≥ 0
x1 = 1/3 dan x2 = –3
Jadi x ≤ –3 atau x ≥ 1/3

(b) │x + 2│ > 2│x – 1│
(x + 2)² > 4(x – 1)²
x² + 4x + 4 > 4(x² – 2x + 1)
x² + 4x + 4 > 4x² – 8x + 4
3x² – 12x < 0
3x(x – 4) < 0
x1 = 0 dan x2 = 4
Jadi 0 < x < 4

Tentukanlah himpunan penyelesaian pertidaksamaan berikut.

|2x – 3| ≤ 7

Jawab:

Dengan menggunakan sifat 1 (b), diperoleh:

−7 ≤ 2x – 3 ≤ 7

⇔ −7 + 3 ≤ 2x ≤ 7 + 3

⇔ −4 ≤ 2x ≤ 10

⇔ −2 ≤ x ≤ 5

Jadi, himpunan penyelesaiannya adalah {x| −2 ≤ x ≤ 5, x ∈ R}.

Tentukan penyelesaian dari pertidaksamaan nilai mutlak berikut.

|2x + 1| ≥ |x – 2|

Jawab:

Dengan menggunakan sifat 2, maka kita peroleh:

√(2x + 1)2 ≥ √(x – 2)2

⇔ (2x + 1)2 ≥ (x – 2)2

⇔ 4x2 + 4x + 1 ≥ x2 – 4x + 4

⇔ 4x2 – x2 + 4x + 4x + 1 – 4 ≥ 0

⇔ 3x2 + 8x – 3 ≥ 0

⇔ (x + 3)(3x – 1) ≥ 0

⇔ x ≤ −3 atau x ≥ 1/3

Jadi, himpunan penyelesaiannya adalah {x| x ≤ −3 atau x ≥ 1/3, x ∈ R}.

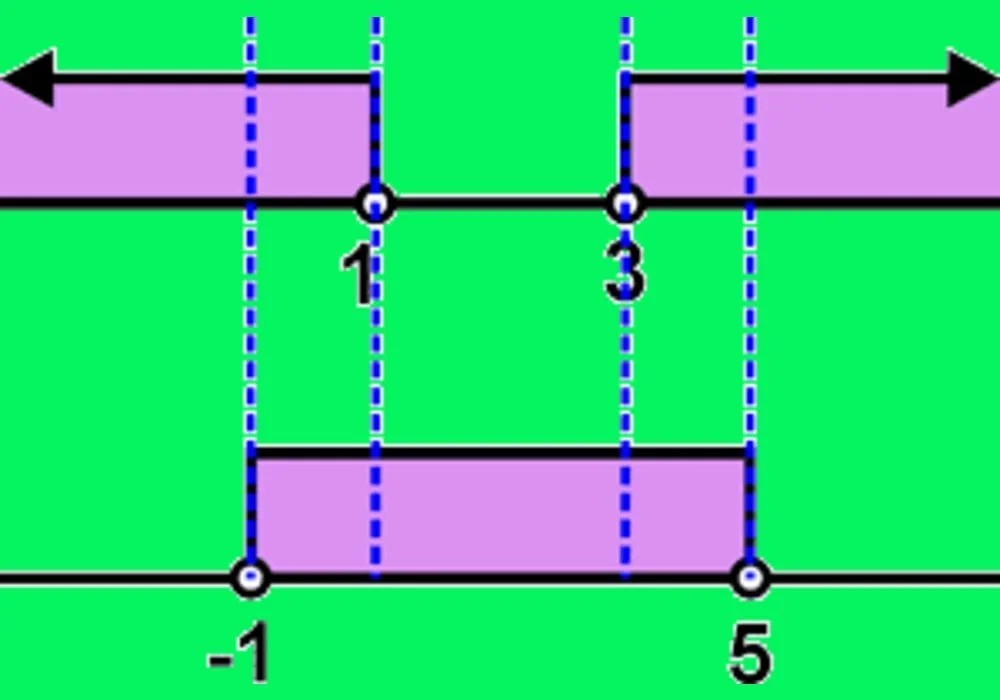
Carilah himpunan penyelesaian dari pertidaksamaan berikut ini dengan menggunakan analisis penyelesaian pada garis bilangan.

|x – 2|2 – 4|x – 2| + 3 < 0

Jawab:

Pertidaksamaan ini dapat kita kerjakan dengan memisalkan bentuk nilai mutlak |x – 2| dalam suatu variabel baru, misalnya a.

Misalkan a = |x – 2| maka pertidaksamaan di atas menjadi:

a2 – 4a + 3 < 0

⇔ (a – 1)(a – 3) < 0

⇔ 1 < a < 3

Karena a = |x – 2| maka 1 < |x – 2| < 3. Bentuk ini dapat dipisahkan menjadi bentuk 1 < |x – 2| dan |x – 2| < 3.

■Untuk 1 < |x – 2| atau |x – 2| > 1

Dengan menggunakan sifat 1 (c) diperoleh:

⇔ x – 2 < −1 atau x – 2 > 1

⇔ x < −1 + 2 atau x > 1 + 2

⇔ x < 1 atau x > 3 ……………….. (1)

■Untuk |x – 2| < 3

Dengan menggunakan sifat 1 (a) diperoleh:

⇔−3 < x – 2 < 3

⇔−3 + 2 < x < 3 + 2

⇔−1 < x < 5 ……………….. (2)

Jika interval (1) dan (2) kita gambarkan dalam garis bilangan, tampak seperti gambar di bawah ini.

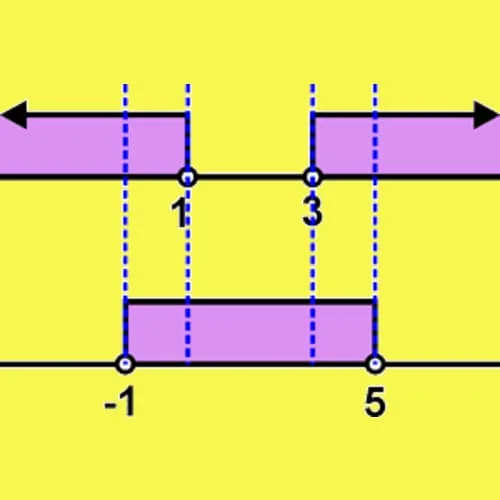
Garis bilangan pertidaksamaan nilai mutlak

Dari garis bilangan di atas, diperoleh himpunan penyelesaian adalah {x| −1 < x < 1 atau 3 < x < 5}.

2. Tentukan nilai x dari pertidaksamaan $|{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|$ !

|{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|

({\sqrt {x^{2}-4x}})^{2}\geq ({\sqrt {3x-10}})^{2}

x^{2}-4x\geq 3x-10

x^{2}-7x+10\geq 0

dibuat harga nol

x^{2}-7x+10=0

(x-2)(x-5)=0

x=2\lor x=5

dibuat irisan

	2		5
+++	N/A	—-	N/A	+++

x\leq 2\lor x\geq 5

karena ada syarat akar maka:

akar 1: $x^{2}-4x\geq 0$

dibuat harga nol

x^{2}-4x=0

x(x-4)=0

x=0\lor x=4

dibuat irisan

	0		4
+++	N/A	—-	N/A	+++

x\leq 0\lor x\geq 4

akar 2: $3x-10\geq 0$; $x\geq {\frac {10}{3}}$

gabungkan umum dan syarat

irisan		(0)		(2)		(10/3)		(4)		(5)
pertama	ya	N/A	ya	N/A	tidak	N/A	tidak	N/A	tidak	N/A	ya
kedua	ya	N/A	tidak	N/A	tidak	N/A	tidak	N/A	ya	N/A	ya
ketiga	tidak	N/A	tidak	N/A	tidak	N/A	ya	N/A	ya	N/A	ya

HP=\{x|x\geq 5,x\in R\}

3. Tentukan nilai x dari pertidaksamaan $|{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|$ !

|{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|

({\frac {x+4}{10-x}})^{2}<({\frac {1}{x-2}})^{2}

({\frac {x+4}{10-x}})^{2}-({\frac {1}{x-2}})^{2}<0

({\frac {x+4}{10-x}}+{\frac {1}{x-2}})({\frac {x+4}{10-x}}-{\frac {1}{x-2}})<0

({\frac {(x+4)(x-2)+10-x}{(10-x)(x-2)}})({\frac {(x+4)(x-2)-(10-x)}{(10-x)(x-2)}})<0

({\frac {x^{2}+2x-8+10-x}{(10-x)(x-2)}})({\frac {x^{2}+2x-8-10+x}{(10-x)(x-2)}})<0

({\frac {x^{2}+x+2}{(10-x)(x-2)}})({\frac {x^{2}+3x-18}{(10-x)(x-2)}})<0

akar dari ${\frac {x^{2}+x+2}{(10-x)(x-2)}}$: ${\frac {x^{2}+x+2}{(10-x)(x-2)}}<0$; $x^{2}+x+2=0$ definit +

karena ada syarat pecahan maka:

penyebut 1: $10-x\neq 0$; $x\neq 10$

penyebut 2: $x-2\neq 0$; $x\neq 2$

akar dari ${\frac {x^{2}+3x-18}{(10-x)(x-2)}}$: ${\frac {x^{2}+3x-18}{(10-x)(x-2)}}<0$; $x^{2}+3x-18<0$

dibuat harga nol

x^{2}+3x-18=0

(x+6)(x-3)=0

x=-6\lor x=3

(tanpa gambar irisan)

karena ada syarat pecahan maka:

penyebut 1: $10-x\neq 0$; $x\neq 10$

penyebut 2: $x-2\neq 0$; $x\neq 2$

dibuat irisan

	-6		2*		3		10*
+++	N/A	—-	N/A	—-	N/A	+++	N/A	+++

nb: * = mempunyai 2 akar

HP=\{x|-6<x<3,x\in R\}

4. Tentukan nilai x dari pertidaksamaan $|x^{2}+x|<12$ !

|x^{2}+x|<12

karena f(x) < g(x) maka penyelesaian -g(x) < f(x) < g(x)

-12<x^{2}+x<12

untuk $-12<x^{2}+x$: $-12<x^{2}+x$; $x^{2}+x+12>0$ definit +

untuk $x^{2}+x<12$: $x^{2}+x<12$; $x^{2}+x-12<0$

dibuat harga nol

x^{2}+x-12=0

(x+4)(x-3)<0

x=-4\lor x=3

dibuat irisan

	-4		3
+++	N/A	—-	N/A	+++

-4<x<3

HP=\{x|-4<x<3,x\in R\}

Bacaan Lainnya

Pangkat Eksponen – Integer – Daftar eksponensial bilangan bulat dan contoh soal dan jawaban

Pangkat Matematika “Tabel dari 1-100” – Pangkat 2, 3, Akar Pangkat 2 dan 3 – Beserta Contoh Soal dan Jawaban

Unduh / Download Aplikasi HP Pinter Pandai

Respons “Ooo begitu ya…” akan sering terdengar jika Anda memasang applikasi kita!

Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!

Sumber bacaan: EduPlace, Math is Fun, Chilimath

Nilai Mutlak (Nilai Absolut) | Persamaan & Pertidaksamaan Contoh Soal dan Jawaban

Penjelasan Persamaan Nilai absolut atau nilai mutlak atau modulus

Persamaan Nilai Mutlak adalah

Dari definisi di atas, nilai absolut a akan selalu positif atau nol, tetapi tidak pernah negatif

Definisi ini sering digunakan untuk menyelesaikan suatu persamaan absolut. Contoh:

Dalam bentuk persamaan mutlak sebagai berikut:

Contoh Soal Persamaan Nilai Mutlak atau Nilai Absolut beserta jawabannya

1. Tentukanlah himpunan penyelesaian dari persamaan |4 – 2/5 x|-7 = 13

2. Tentukan nilai x dari persamaan <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cbc0bcb9f23f4a4dcc21952d73ecccae14298b5b" alt="{\displaystyle |x^{2}+x|=12}" aria-hidden="true" />!

3. Tentukan nilai x dari persamaan <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/cb3e7e6757f3f916bf73cb5c0aae7c868eab16f2" alt="{\displaystyle |{\sqrt {x^{2}-4x}}|=|{\sqrt {3x-10}}|}" aria-hidden="true" />!

4. Tentukanlah sebuah himpunan penyelesaian dari |3x – 7| = 3

5. Tentukan nilai x dari |3x+2|²+|3x+2|-2=0

6. Tentukan nilai x dari persamaan <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/e3c5a12e8ceeda2585b991882b01bffc7230ea37" alt="{\displaystyle |x^{2}-4x-12|-|7-6x|=5}" aria-hidden="true" />!

7. Tentukanlah himpunan dari |3x – 1| = |x + 4|

8. Selesaikanlah persamaan -3|x-4|+5 = 14

9. Tentukan nilai x yang memenuhi |2x+16|=x+4

10. Tentukanlah himpunan penyelesaian |4x + 2| ≥ 6

11. Tentukan penyelesaian dari |x-2| = |6+2x|

12. Tentukan nilai x dari persamaan <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/42fc38b4f34db10c1a49dbce109f2e204fc3edb3" alt="{\displaystyle |{\frac {x+4}{10-x}}|=|{\frac {1}{x-2}}|}" aria-hidden="true" />!

Penjelasan Pertidaksamaan Mutlak

Langkah-langkah Menyelesaikan Pertidaksamaan Nilai Mutlak

Contoh Soal dan Jawaban Pertidaksamaan Nilai mutlak

1. Tentukan nilai x dari persamaan <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/64f34ceec60536edd4dc354ef5e330463893871b" alt="{\displaystyle |x^{2}-4x-12|-|7-6x|\geq 5}" aria-hidden="true" />!

keempat batas-batas akan dibuat irisan

Tentukanlah interval penyelesaian pertidaksamaan berikut ini : (a) │x – 6│ ≤ 9 (b) │x + 2│ > 4

02. Tentukanlah interval penyelesaian pertidaksamaan berikut ini : (a) │2x + 1│ ≥ │x – 2│ (b) │x + 2│ > 2│x – 1│

Tentukanlah himpunan penyelesaian pertidaksamaan berikut.

|2x – 3| ≤ 7

Tentukan penyelesaian dari pertidaksamaan nilai mutlak berikut.

|2x + 1| ≥ |x – 2|

Carilah himpunan penyelesaian dari pertidaksamaan berikut ini dengan menggunakan analisis penyelesaian pada garis bilangan.

|x – 2|2 – 4|x – 2| + 3 < 0

2. Tentukan nilai x dari pertidaksamaan <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/f1de5f86f3859901a63206e77dda8e49bc8179e3" alt="{\displaystyle |{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|}" aria-hidden="true" />!

3. Tentukan nilai x dari pertidaksamaan <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/249185aa2b5392673e59281792ecfd51c5cbb87f" alt="{\displaystyle |{\frac {x+4}{10-x}}|&lt;|{\frac {1}{x-2}}|}" aria-hidden="true" />!

4. Tentukan nilai x dari pertidaksamaan <img decoding="async" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4945faa25c905a7e17d7182aabdb8411b058bb9c" alt="{\displaystyle |x^{2}+x|&lt;12}" aria-hidden="true" />!

Bacaan Lainnya

Unduh / Download Aplikasi HP Pinter Pandai

Nilai Pi 1 juta digit pertama | Analisis dan…

Menghitung Dimensi Balok dari Luas Jaring-Jaringnya

Rumus Matematika dan Contoh untuk Penggunaan Sehari-hari

Tinggalkan Balasan Batalkan balasan

2. Tentukan nilai x dari persamaan $|x^{2}+x|=12$ !

3. Tentukan nilai x dari persamaan $|{\sqrt {x^{2}-4x}}|=|{\sqrt {3x-10}}|$ !

6. Tentukan nilai x dari persamaan $|x^{2}-4x-12|-|7-6x|=5$ !

12. Tentukan nilai x dari persamaan $|{\frac {x+4}{10-x}}|=|{\frac {1}{x-2}}|$ !

1. Tentukan nilai x dari persamaan $|x^{2}-4x-12|-|7-6x|\geq 5$ !

Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) │x – 6│ ≤ 9
(b) │x + 2│ > 4

02. Tentukanlah interval penyelesaian pertidaksamaan berikut ini :
(a) │2x + 1│ ≥ │x – 2│
(b) │x + 2│ > 2│x – 1│

2. Tentukan nilai x dari pertidaksamaan $|{\sqrt {x^{2}-4x}}|\geq |{\sqrt {3x-10}}|$ !

3. Tentukan nilai x dari pertidaksamaan $|{\frac {x+4}{10-x}}|<|{\frac {1}{x-2}}|$ !

4. Tentukan nilai x dari pertidaksamaan $|x^{2}+x|<12$ !