Geometri Analitik

Geometri analitik, juga dikenal sebagai geometri koordinat atau geometri kartesian, adalah ilmu yang mempelajari geometri menggunakan sistem koordinat. Ini kontras dengan geometri sintetis. Geometri analitik digunakan dalam fisika dan teknik dan juga dalam penerbangan, peroketan, ilmu ruang angkasa dan penerbangan luar angkasa.

Baca juga: Koordinat Kartesius, Koordinat persegi | Contoh Soal dan Jawaban

Persamaan dan Kurva dalam Geometri Analitik

Dalam geometri analitik, setiap persamaan yang melibatkan koordinat menentukan bagian dari bidang, yaitu kumpulan solusi untuk persamaan, atau lokus. Misalnya, persamaan y = x sesuai dengan himpunan semua titik pada bidang yang koordinat x dan koordinat y-nya sama. Titik-titik ini membentuk garis, dan y = x disebut sebagai persamaan untuk garis ini. Secara umum, persamaan linier yang melibatkan garis x dan y menentukan, persamaan kuadrat menentukan bagian berbentuk kerucut, dan persamaan yang lebih rumit menggambarkan gambar yang lebih rumit.

Biasanya, satu persamaan sesuai dengan kurva di bidang. Ini tidak selalu terjadi: persamaan trivial x = x menentukan seluruh bidang, dan persamaan x2 + y2 = 0 hanya menentukan titik tunggal (0, 0). Dalam tiga dimensi, persamaan tunggal biasanya memberikan permukaan, dan kurva harus ditentukan sebagai perpotongan dua permukaan (lihat di bawah), atau sebagai sistem persamaan parametrik.

Persamaan x2 + y2 = r2 adalah persamaan untuk setiap lingkaran yang berpusat pada titik asal (0, 0) dengan jari-jari r.

Garis dan Bidang dalam Geometri Analitik

Garis dalam bidang Cartesian, atau lebih umum lagi, dalam koordinat affine, dapat dijelaskan secara aljabar dengan persamaan linier. Dalam dua dimensi, persamaan untuk garis non-vertikal sering kali diberikan dalam bentuk titik potong-gradien:

y = mx + b

yang dimana:

m adalah kemiringan atau kemiringan garis.
b adalah perpotongan garis dengan sumbu y.
x adalah variabel independen dari fungsi y = f (x).

Dengan cara yang dianalogikan dengan garis-garis jalan dalam ruang dua dimensi yang dideskripsikan menggunakan bentuk kemiringan titik untuk persamaannya, bidang-bidang dalam ruang tiga dimensi memiliki deskripsi alami menggunakan titik pada bidang dan vektor ortogonal untuk itu ( vektor normal) untuk menunjukkan “kecenderungan” nya.

Secara spesifik, misalkan r0 menjadi vektor posisi suatu titik P0 = (x0, y0, z0) dan misalkan n = (a,b,c) adalah vektor bukan nol.

Bidang yang ditentukan oleh titik dan vektor ini terdiri dari titik-titik tersebut P, dengan vektor posisi r, sehingga vektor yang ditarik dari P0 ke tegak lurus terhadap n. Mengingat bahwa dua vektor tegak lurus jika dan hanya jika hasil kali titiknya nol, maka bidang yang diinginkan dapat digambarkan sebagai himpunan semua titik r sedemikian rupa sehingga

n.(r-r0) = 0

(Titik di sini berarti perkalian titik, bukan perkalian skalar.) Memperluas ini menjadi:

a(x-x0) + b(y-y0) + c(z-z0) = 0

yang merupakan bentuk normal dari persamaan bidang. Ini hanyalah persamaan linier:

ax + by + cz + d = 0, yang dimana d = -(ax0 + by0 + cz0)

Sebaliknya, dengan mudah ditunjukkan bahwa jika a, b, c dan d adalah konstanta dan a, b, dan c tidak semuanya nol, maka grafik persamaan

ax + by + cz + d = 0

adalah bidang yang memiliki vektor n=(a,b,c) sebagai normal. Persamaan umum untuk bidang ini disebut bentuk umum persamaan bidang.

Dalam bidang tiga dimensi, garis tidak dapat dijelaskan dengan persamaan linier tunggal, sehingga sering kali digambarkan dengan persamaan parametrik:

x = x0 + at
y = y0 + bt
z= z0 + ct

di mana:

x, y, dan z adalah semua fungsi dari variabel independen t yang berkisar di atas bilangan real.
(x0, y0, z0) adalah titik mana pun pada garis.
a, b, dan c terkait dengan kemiringan garis garis, sehingga vektor (a, b, c) sejajar dengan garis.

Irisan kerucut dalam Geometri Analitik

Dalam sistem koordinat Kartesius, grafik persamaan kuadrat dalam dua variabel selalu berupa penampang berbentuk kerucut – meskipun dapat merosot, dan semua bagian berbentuk kerucut muncul dengan cara ini. Persamaannya akan berbentuk

Ax² + Bxy + Cy² + Dx + Ey + F = 0 dengan A, B, C tidak semuanya nol

Karena penskalaan keenam konstanta menghasilkan lokus nol yang sama, kerucut dapat dianggap sebagai titik dalam ruang proyektif lima dimensi P5.

Bagian berbentuk kerucut yang dijelaskan oleh persamaan ini dapat diklasifikasikan menggunakan diskriminan

B² – 4AC

Jika kerucut tidak berdegenerasi, maka:

• jika B² – 4AC<0, persamaan tersebut mewakili elips;
• jika A = C dan B = 0, persamaan tersebut mewakili lingkaran, yang merupakan kasus khusus untuk elips;
• jika B² -4AC = 0, persamaan tersebut mewakili parabola;
• jika B² -4AC> 0, persamaan tersebut mewakili hiperbola;
• jika kita juga memiliki A + C = 0, persamaan tersebut mewakili hiperbola persegi panjang.

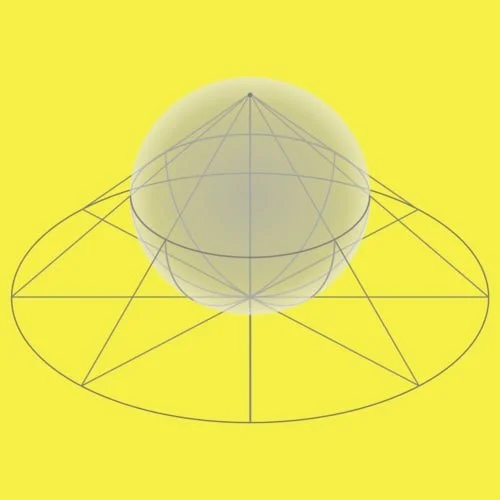
Permukaan kuadrik atau kuadrat

Permukaan kuadrik, atau kuadrat, adalah permukaan 2 dimensi dalam ruang 3 dimensi yang didefinisikan sebagai lokus nol dari polinomial kuadrat. Dalam koordinat x1, x2, x3, kuadrat umum ditentukan oleh persamaan aljabar

^3 Σ {i, j = 1} xi Qij xj + ^3 Σ {i, j = 1} Pi xi + R = 0

atau

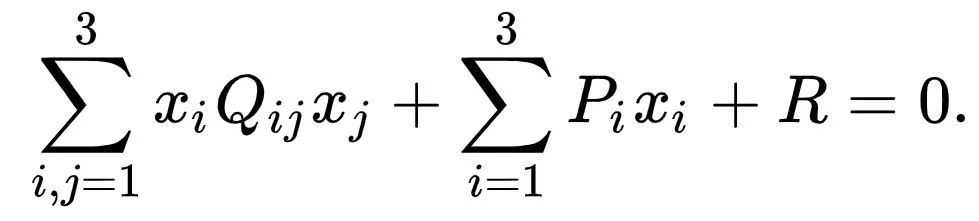
Permukaan kuadrat meliputi elipsoid (termasuk bola), paraboloids, hiperboloid, silinder, kerucut dan bidang (geometri).

Jarak dan Sudut

Dalam geometri analitik, pengertian geometri seperti jarak dan ukuran sudut didefinisikan menggunakan rumus. Definisi ini dirancang agar konsisten dengan geometri Euclidean yang mendasari. Misalnya, dengan menggunakan koordinat Kartesius di pesawat, jarak antara dua titik (x1, y1) dan (x2, y2) ditentukan dengan rumus

yang dapat dilihat sebagai versi dari teorema Pythagoras. Demikian pula, sudut yang dibuat garis dengan horizontal dapat ditentukan dengan rumus

θ = arctan(m)

yang dimana m adalah kemiringan garis.

Dalam tiga dimensi, jarak diberikan oleh generalisasi teorema Pythagoras:

d = √(x2 x1)² + (y2 y1)² + (z2 z1)²

while the angle between two vectors is given by the dot product. The dot product of two Euclidean vectors A and B is defined by

sedangkan sudut antara dua vektor diberikan oleh perkalian titik. Produk titik dari dua vektor Euclidean A dan B ditentukan oleh

dimana θ adalah sudut antara A dan B.

Transformasi

Transformasi diterapkan ke fungsi induk untuk mengubahnya menjadi fungsi baru dengan karakteristik serupa.

Grafik R (x, y) diubah dengan transformasi standar sebagai berikut:

• Mengubah x menjadi x-h memindahkan grafik ke kanan h unit.
• Mengubah y menjadi y-k memindahkan grafik ke atas k unit.
• Mengubah x menjadi x/b akan meregangkan grafik secara horizontal dengan faktor b. (anggaplah sebagai x dilatasi)
• Mengubah y menjadi y/a akan meregangkan grafik secara vertikal.
• Mengubah x menjadi x cos A + ysin A dan mengubah y menjadi x sin A + y cos A memutar grafik dengan suatu sudut A.

Terdapat transformasi standar lain yang biasanya tidak dipelajari dalam geometri analitik dasar karena transformasi mengubah bentuk objek dengan cara yang biasanya tidak dipertimbangkan. Kemiringan adalah contoh transformasi yang biasanya tidak dipertimbangkan.

Contoh Soal + Jawaban Geometri Analitik

1. Tentukan jarak antara A (5, -3) dan B (2, 1).

Jawaban:

Jarak antara dua titik A(x1,y1) dan B(x2,y2) dirumuskan dengan:

Jarak = √(x2-x1)² + (y2-y1)²

AB = √(5-2)² + (-3-1)²
= √3² + (-4)² = √9+16
= √25 = 5

2. Temukan persamaan garis yang melewati A (4, -1) dan sejajar sumbu x.

Jawaban:

Kemiringan garis yang sejajar dengan sumbu x adalah nol. Jadi:

y+1 = 0(x-4) → y+1 = 0 → y = -1

3. Tentukan nilai m, sehingga D1, D2, D3 saling bertemu pada satu titik.
D1: x – y = 1
D2: 2x + y = 5
D3: (2m – 5)x – my = 3

Jawaban:

D1​: x−y=1
D2 = 2x + y = 5
→ 3x = 6 → x = 2,y = 1
(2m – 5)x – my = 3 → (2m – 5)2 – m = 3 → 4m – 10 – m = 3 → 3m =13 → m = 13/3

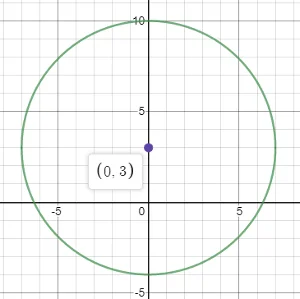
3. Dimana P (pusatnya) dan berapa jari-jari lingkarannya x² + (y-3)² = 49 ? dan buatlah grafiknya!

A. P: (0-3) r = 49
B. P : (3,0) r = 49
C. P: (+3,0) r = 7
D. P: (0,3) r = 7

Jawaban:

Bentuk kanonik dari persamaan lingkaran adalah
(x-h)² + (y-k)² yang dimana pusatnya P : (h,k) dan jari-jari r
Kita memiliki x² + (y-3)² = 49
Jadi, pusatnya di (0,3) dan r = 7 (0,3) r = 7

4. Perpotongan parabola (y+4)² = 4 (x+1) dengan sumbu koordinat berada pada?

A. (0,2); (0,6); (-3,0)
B. (0,2); (0,6); (3,0)
C. (0,-2); (0,6); (3,0)
D. (0,2); (0,+6); (-3,0)

Jawaban:

(y+4)² = 4(x+1)
Jika x = 0x = 0 maka (y + 4)² = 4 (y + 4)
y+4 = ±2 ⇒ y = -2 dan y = -6 adalah  y – perpotongan sumbu y-sumbu.
Ketika y = 0,4 (x+1) = 16 ⟹ x = 3
Maka jawabannya adalah (0, -2); (0, -6); (3,0)

5. Identifikasi bagian kerucut yang diwakili oleh persamaan 2x² – 2xy + 2y² = 1

A. Elips
B. Parabola
C. Hyperbola
D. Lingkaran

Jawaban:

2x² – 2xy + 2y² = 1
Persamaan umum untuk setiap bagian kerucut adalah
Ax² + Bxy + Cy² + Dx + Ey + F = 0
A= 4
B=-2
C=2
Diskriminan adalah
B² −4AC = 4 −4 (2) (2) = -12 <0
Bagian berbentuk kerucut adalah elips.

6. Ubah persamaan y = 10y = 10 menjadi bentuk kutub!

A. r = 10 sin θ
B. r = tan 10/π
C. r = 10/sin θ
D. r = 10tan 10/π

Jawaban:

y = 10 ⟹ y = r sin θ = 10 ⟹ r = 10/sin θ = 10 csc θ

Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing