Rumus Fungsi Kuadrat
Berikut rumus-rumus fungsi kuadrat:
Rumus umum fungsi kuadrat
y = f(x) = ax² + bx + c
Diskriminan
D = b² – 4.a.c
Sumbu simetri
x = – b/2a
Nilai ekstrim
y = – D/4a = f (-b/2a)
Titik balik/puncak
(x,y) = (-b/2a, – D/4a)
Titik potong pada sumbu x
(x1,0) dan (x2,0)
Titik potong pada sumbu y
(x,y) = (O,c)
Bentuk parabola
a>0 : terbuka ke atas
a<0 : terbuka ke bawah
Keterangan:
- Bentuk umum: syarat a≠0.
- Titik potong pada sumbu x: x1 dan x2 merupakan akar dari ax²+bx+c=0.
- Titik potong pada sumbu y: jika x = 0, maka y = a(0)² + b(0) + c = c.
Persamaan fungsi kuadrat
Persamaan fungsi kuadrat : dimana f(x) = y maka titik balik (titik puncak) fungsi kuadrat adalah ( , ).
- Pembuktian
Dari bentuk umum persamaan kuadrat,
anggapan bahwa adalah 0 maka:
- atau
maka titik balik adalah ( , ).
Penjelasan Fungsi Kuadrat
Di dalam aljabar, fungsi kuadrat, polinomial kuadratis, polinomial berderajat 2, atau sederhananya kuadratis, adalah fungsi polinomial yang memuat satu variabel atau lebih, di mana derajat tertinggi suku sama dengan dua.
Misalnya, fungsi kuadrat dengan tiga variabel x, y, dan z secara eksklusif memuat suku-suku x2, y2, z2, xy, xz, yz, x, y, z, dan sebuah konstanta:
dengan paling sedikit satu dari koefisien a, b, c, d, e, atau f dari suku-suku berderajat dua tidak sama dengan nol.
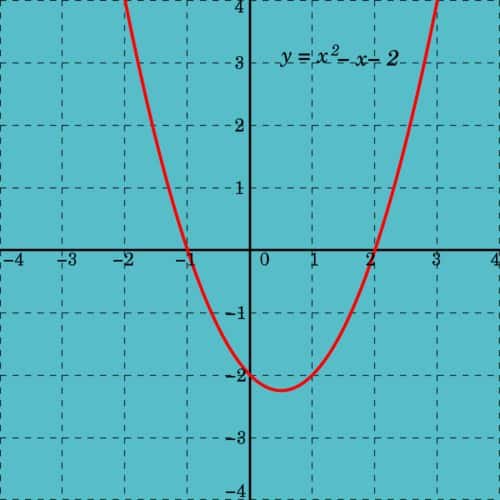
Suatu fungsi kuadrat univariate (bervariabel tunggal) memiliki bentuk:
di dalam variabel tunggal x. Grafik fungsi kuadrat univariat adalah parabola yang sumbu simetrinya sejajar dengan sumbu-y, seperti ditunjukkan dalam ilustrasi di kanan.
Jika suatu fungsi kuadrat ditetapkan sama dengan nol, maka hasilnya adalah persamaan kuadrat. Penyelesaian untuk persamaan univariat disebut akar fungsi univariat.
Kasus bivariat dalam suku-suku variabel x dan y memiliki bentuk:
dengan paling sedikit satu dari a, b, c tidak sama dengan nol, dan suatu persamaan yang menetapkan fungsi ini sama dengan nol akan menghasilkan irisan kerucut (lingkaran atau elips, parabola, atau hiperbola).
Secara umum, bisa terdapat sejumlah besar variabel sembarang, di mana kasus yang menghasilkan permukaan disebut kuadrik, tetapi suku berderajat tertinggi haruslah 2, seperti x2, xy, yz, dan dst.
Contoh Soal dan Jawaban Fungsi Kuadrat
1. Diketahui grafik fungsi y = (m -3) x2 + 4x – 2m merupakan fungsi definit negatif. Batas-batas nilai m yang memenuhi adalah…
a. m < 3
b. m > 3
c. 1 < m < 2
d. 1 < m < 3
e. 2 < m < 3
Jawaban : C
Pembahasan :
Definit negatif jika D < 0 dan a < 0
1) m – 3 < 0 maka m < 3
2) D < 0 maka b2 – 4ac < 0

Sehingga 1 < m < 2
Dari 1) dan 2) diperoleh 1 < m < 2
2. Tentukan sumbu simetri grafik fungsi kuadrat y = 5x2 – 20x + 1.
Sumbu simetri suatu fungsi kuadrat dapat dihitung dengan rumus x = -b/2a. Dari fungsi kuadrat pada soal diperoleh a = 5 dan b = -20.
x = -b/2a
⇒ x = -(-20)/2(5)
⇒ x = 20/10
⇒ x = 2
Jadi sumbu simetri untuk fungsi kuadrat y = 5x2 – 20x + 1 adalah x = 2.
3. Sebuah grafik fungsi kuadrat memotong sumbu –x di A ( 1, 0 ) dan B ( 2, 0 ). Jika grafik tersebut juga melewati titik ( 0, 4 ), maka tentukanlah persamaan fungsi kuadratnya!
Penyelesaian :
Persamaan fungsi kuadrat bisa dinyatakan menjadi y = a ( x – 1 )
( x – 2 ). Nilai a ditentukan dari keterangan bahwa fungsi kuadrat itu lewat titik ( 0, 4 ). Maka artinya untuk nilai x = 0 didapatkan y = 4.
y = a ( x – 1 ) ( x – 2 )
4 = a ( 0 – 1 ) ( 0 – 2 )
4 = a ( -1 ) ( -2 )
4 = 2a
a = 2
Maka dari itu, persamaan fungsi kuadratnya adalah seperti di bawah ini:
y = f ( x )
y = a ( x – 1 ) ( x – 2 )
y = 2 ( x – 1 ) ( x – 2 )
y = 2 ( x² – x – 2x + 2 )
y = 2 ( x² – 3x + 2 ?)
y = 2x² – 6x + 4
4. Jika grafik fungsi y = x2 + px + k mempunyai titik puncak (1,2), maka tentukan nilai p dan k.
Dari y = x2 + px + k diperoleh a = 1, b = p dan c = k.
Titik puncak (1,2) maka x = 1 dan y = 2.
x = -b/2a = 1
⇒ -b/2a = 1
⇒ -p/2 =1
⇒ p = -2
y = y(-b/2a) = y(1) = 2
⇒ x2 + px + k = 2
⇒ (1)2 + -2(1) + k = 2
⇒ 1 – 2 + k = 2
⇒ k = 2 + 1
⇒ k = 3
Jadi, p = -2 dan k = 3.
5. Tentukan koordinat titik balik dari grafik fungsi kuadrat yang persamaannya y = (x – 6)(x + 2).
y = (x – 6)(x + 2)
⇒ y = x2 + 2x – 6x – 12
⇒ y = x2 – 4x – 12
Dari persamaan di atas diperoleh a = 1 dan b = -4.
Titik balik fungsi kuadrat dapat ditentukan dengan (x,y) = (-b/2a, F(-b/2a)).
x = -b/2a
⇒ x = -(-4)/2(1)
⇒ x = 4/2
⇒ x = 2
y = F(-b/2a) = F(x)
⇒ y = F(2)
⇒ y = 22 – 4(2) – 12
⇒ y = 4 – 8 – 12
⇒ y = -16
Jadi, titik balik fungsi kuadrat y = (x – 6)(x + 2) adalah (2,-16).
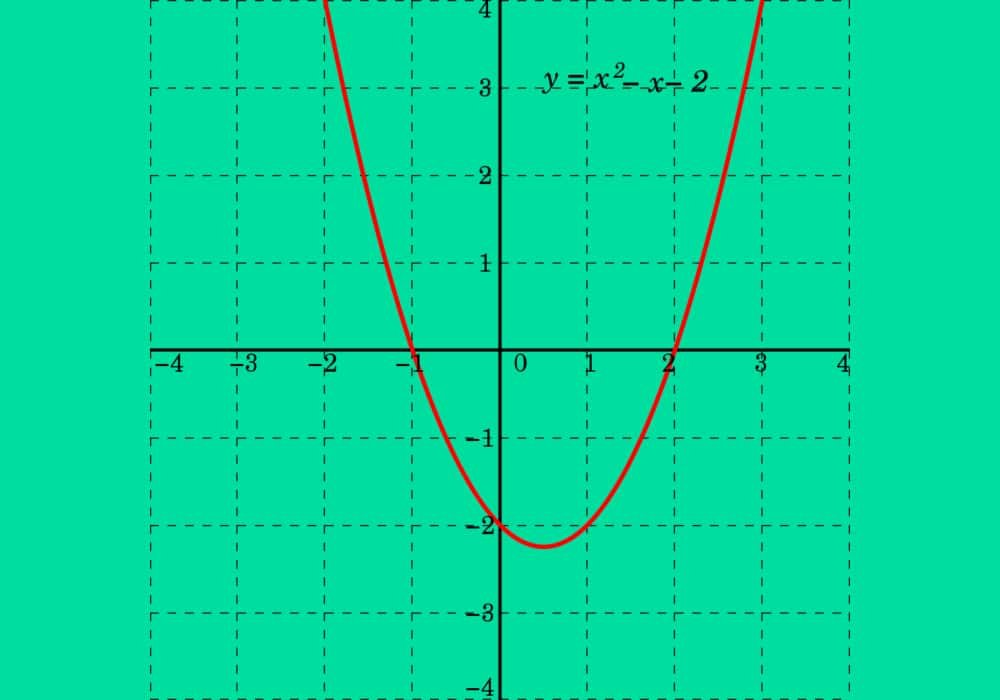
6. Tentukan koordinat titik potong grafik fungsi kuadrat y = 3x2 – x – 2 dengan sumbu x dan sumbu y.
Titik potong pada sumbu x dapat diperoleh jika y = 0.
3x2 – x – 2 = 0
⇒ (3x + 2)(x – 1) = 0
⇒ x1 = -2/3 dan x2 = 1
Maka titik potongnya (-2/3,0) dan (1,0).
Titik potong pada sumbu y dapat diperoleh dengan x = 0.
⇒ y = 3x2 – x – 2
⇒ y = 3(0)2 – (0) – 2
⇒ y = -2
Maka titik potongnya (0,-2).
7. Jika diketahui fungsi kuadrat f(x)=2×2−7x−5 serta titik A(2,−11), B(−1,0), dan C(−4,55). Maka titik yang dilalui grafik fungsi f(x) adalah…
A. titik A,B, dan C
B. titik A dan B
C. titik A dan C
D. titik A saja
E. titik C saja
Titik dilalui oleh grafik fungsi apabila substitusi nilai x pada rumus fungsi menghasilkan nilai y.
Diketahui f(x)=2×2−7x−5.
Periksa titik :
Substitusi pada f(x), diperoleh
Diperoleh y=−11 sehingga titik A dilalui oleh grafik fungsi f(x).
Periksa titik B(−1,0):
Substitusi pada , diperoleh
Diperoleh sehingga titik tidak dilalui oleh grafik fungsi f(x).
Periksa titik C(−4,55):
Substitusi x=−4 pada f(x), diperoleh
Diperoleh y=55 sehingga titik C dilalui oleh grafik fungsi .
Jadi, titik yang dilalui adalah titik dan C.
(Jawaban C)
8. Tentukan titik balik fungsi kuadrat F(x) = 2(x + 2)2 + 3.
Uraikan terlebih dahulu fungsi kuadrat di atas menjadi :
F(x) = 2(x + 2)2 + 3
⇒ F(x) = 2(x2 + 4x + 4) + 3
⇒ F(x) = 2x2 + 8x + 8 + 3
⇒ F(x) = 2x2 + 8x + 11
Dari fungsi di atas diperoleh a = 2, b = 8.
Titik balik fungsi kuadrat dapat ditentukan dengan (x,y) = (-b/2a, F(-b/2a)).
x = -b/2a
⇒ x = -8/2(2)
⇒ x = -8/4
⇒ x = -2
y = F(-b/2a) = F(x)
⇒ y = F(-2)
⇒ y = 2(-2)2 + 8(-2) + 11
⇒ y = 2(4) – 16 + 11
⇒ y = 8 – 16 + 11
⇒ y = 8 – 16 + 11
⇒ y = 3
Jadi, titik balik untuk fungsi kuadrat F(x) = 2(x + 2)2 + 3 adalah (-2,3).
Cara Menggambar Grafik Fungsi Kuadrat
1. Tentukan titik potong terhadap sumbu x.
2. Tentukan titik potong terhadap sumbu y.
3.Tentukan titik balik.
4.Tarik garis parabola
Keterangan:
Fungsi kuadrat: F(x) ax² + bx + c , a ≠ 0.
- Untuk tiktik potong terhadap sumbu x (jika ada), maka merupakan akar dari ax² + bx + c = 0.
- Untuk tiktik potong terhadap sumbu y, maka x = 0, sehingga y = a(0) + b(0) + c = c → titik (0,c).
- Titik balik dapat dapat berupa titik maksimum (grafik terbuka ke bawah) atau minimum (terbuka ke atas).
Contoh Soal Grafik Fungsi Kuadrat dan Jawabannya
1. Jika grafik fungsi kuadrat menyinggung garis dengan , maka nilai yang memenuhi adalah…
A. 55
B. 44
C. 33
D. 22
E. 11
Substitusikan f(x)=y=x2+x+p ke persamaan 3x+y=1, sehingga diperoleh
3x+(x²+x+p)=1
x²+4x+(p-1)=0
Karena grafik fungsi kuadrat (parabola) dan garisnya bersinggungan, maka diskriminan dari persamaan kuadrat di atas bernilai 0.
D=b²−4ac=0
(4)²−4(1)(p−1)=0
16−4p+4=0
4p=20
p=5
Jadi, nilai p adalah 5
(Jawaban A)
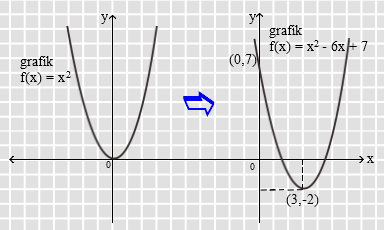
2. Ke arah manakah grafik fungsi f(x) = x2 harus digeser untuk memperoleh grafik fungsi kuadart f(x) = x2 – 6x + 7.
Fungsi kuadrat f(x) = x2 memiliki nilai :
⇒ a > 0 sehingga parabola terbuka ke atas.
⇒ b = 0 sehingga titik balik parabola berada pada sumbu y.
⇒ c = 0 sehingga grafik parabola melalui titik (0,0).Fungsi kuadrat f(x) = x2 – 6x + 7 memiliki nilai :
⇒ a > 0 sehingga parabola terbuka ke atas
⇒ b = -6 maka a.b = -6 < 0 sehingga titik balik ada di kanan sumbu y.
⇒ c = 7 > 0 sehingga parabola memotong sumbu y di atas sumbu x.
Karena titik balik ada di kanan sumbu y, berarti grafik f(x) = x2 harus digeser ke arah kanan sumbu x. Untuk lebih jelasnya kita dapat menentukan terlebih dahulu titik-titik yang dibutuhkan, yaitu :
⇒ sumbu simetri = x = -b/2a = -(-6)/2(1) = 3
⇒ nilai ekstrim = y = f(-b/2a) = f(3) = 32 – 6(3) + 7 = -2
⇒ titik balik = (x,y) = (3,-2)
Ingat bahwa grafik f(x) = x2 melalui titik (0,0) sedangkan grafik f(x) = x2 – 6x + 7 melalui titik (3,-2), maka kita dapat menggambar grafik fungsi kuadrat f(x) = x2 – 6x + 7 dengan menggeser grafik fungsi kuadrat f(x) = x2 ke arah kanan sumbu x sejauh 3 satuan dan ke arah bawah sumbu y sejauh 2 satuan seperti gambar di bawah ini :
3. Grafik fungsi y=ax²+bx−1 memotong sumbu-X di titik (12,0) dan (1,0). Fungsi ini mempunyai nilai ekstrem…
A. maksimum 3/8
B. minimum −3/8
C. maksimum -2/8
D. maksimum 1/8
E. minimum −1/8
F. maksimum 5/8
Pembahasan:
Secara aljabar, kasus di atas dapat dimisalkan sebagai suatu persamaan kuadrat yang memiliki akar x1=1/2 dan x2=1, sehingga ditulis
(x−1/2)(x−1)=0
x²−32/x+1/2=0
Kalikan kedua ruas dengan −2
−2x²+3x−1=0
Bandingkan dengan rumus fungsi y=ax²+bx−1.
Dari sini, diperoleh a=−2a=−2 dan b=3.
Karena koefisien x², yaitu a, bernilai negatif, maka parabola (grafik fungsi) akan terbuka ke bawah sehingga nilai ekstremnya maksimum yaitu
yp=−D/4a
=−b²−4ac/4a
=[−3²−4(−2)(−1)] / [4(−2)]
=−[9−8] / [−8] =1/8
Jadi, nilai ekstrem fungsi tersebut adalah maksimum 1/8
(Jawaban D)
4. Gambarkan grafik fungsi kuadrat y = x2 + 2x + 5.
Dari soal diperoleh a = 1, b = 2 dan c = 5. Tentukan titik-titik yang dibutuhkan, yaitu :
⇒ sumbu simetri = x = -b/2a = -2/2(1) = -1
⇒ nilai ekstrim = y = f(-1) = (-1)2 + 2(-1) + 5 = 4
⇒ titik balik = (x,y) = (-1,4) berarti parabola tidak memotong sumbu x.
⇒ titik potong pada sumbu y = (0,c) = (0,5)
maka grafik untuk y = x2 + 2x + 5 adalah seperti berikut ini :
Jika dianalisis berdasarkan nilai a, b, c dan diskriminan, kita dapat membuktikan bahwa grafik di atas sesuai atau tidak.
⇒ a = 1 → a > 0 : parabola terbuka ke atas.
⇒ b = 2 → a.b = 1(2) = 2 → a.b > 0 : titik balik di kiri sumbu y.
⇒ c = 5 → c > 0 : parabola memotong sumbu y di atas sumbu x.
⇒ D = b2 – 4ac = 4 – 4(1)(5) = – 16 : grafik tidak memotong sumbu x karena D < 0.
5. Tentukan persamaan grafik fungsi kuadrat yang mempunyai titik balik minimum (1,2) dan melalui titik (2,3).
Misalkan fungsi kuadrat f(x) = ax2 + bx + c maka kita harus mencari nilai a, b, dan c.
sumbu simetri = x = 1
⇒ -b/2a = 1 maka b = -2a
nilai ekstrim = y = 2
⇒ f(-b/2a) = 2
⇒ a(1)2 + b(1) + c = 2
⇒ a + b + c = 2 → ganti b dengan -2a.
⇒ a – 2a + c = 2
⇒ -a + c = 2Melalui titik (2,3), maka :
⇒ f(2) = 3
⇒ a(2)2 + b(2) + c = 3
⇒ 4a + 2b + c = 3
⇒ 4a + 2(-2a) + c = 3
⇒ 4a – 4a + c = 3
⇒ c = 3
Substitusi nilai c = 3 ke persamaan -a + c = 2.
⇒ -a = -1
⇒ a = 1
Karena a = 1 maka :
⇒ b = -2a
⇒ b = -2(1)
⇒ b = -2
Jadi fungsi kuadrat yang grafiknya melalaui titik (2,3) dan titik balik minimum (1,2) adalah : x2 – 2x + 3.
Bacaan Lainnya
- Persamaan Pangkat 3 – Fungsi Kubik – Matematika Aljabar – Beserta Contoh Soal dan jawaban
- Akar Kuadrat / Pangkat – Penjelasan, Contoh Soal dan Jawaban
- Quiz Matematika- 4√16 + 4√16 = jawaban A, B, C atau D ? - Penyederhanaan Akar Kuadrat
- Pangkat Matematika – Tabel dari 1-100 – Pangkat 2, 3, Akar Pangkat 2 dan 3 – Beserta Contoh Soal dan Jawaban
- Nilai Pi 1 juta digit pertama π
- Nilai Pi Yang Tepat π – 100 000 digit pertama
- Perbandingan Rasio Matematika – Rumus, Contoh Soal dan Jawaban
- Faktoradik Matematika – Nilai, Cara, Kode Program dan Contohnya
- Rumus Geometri – Contoh Soal dan Jawaban – Segi tiga, Persegi, Trapesium, Layang-layang, Jajaran Genjang, Belah ketupat, Lingkaran, Prisma, Balok, Kubus, Tabung, Limas, Bola
- Rumus Volume (Isi) Matematika – rumus volume untuk: kubus, balok, silinder, limas, kerucut, bola, ellipsoid, torus, tetrahedron, tarallelepiped, volume benda putar…
- Sudut Matematika dan Radian – Geometri – Soal Jawaban
- Rumus Turunan Matematika – TABEL TURUNAN DIFERENSIAL KALKULUS – Beserta Contoh Soal dan Jawaban
- Rumus-Rumus Lingkaran – Volume – Tes Matematika Lingkaran
- Induksi Elektromagnetik – Hukum Faraday dan Hukum Lenz – Soal dan Jawaban
- Rumus Induktansi, Induktor dan Energi Medan Magnet – Soal dan Jawaban
- Induksi dan Fluks Magnetik Bersama Contoh Soal dan Jawaban
- Rumus Rangkaian Listrik Dan Contoh-Contoh Soal Beserta Jawabannya
- Tabel Konstanta Fisika – Tabel konstanta universal, elektromagnetik, atom dan nuklir, fisika-kimia, nilai yang diadopsi, satuan natural, bilangan tetap
- Rumus Fisika: Alat optik: Lup, Mikroskop, Teropong Bintang, Energi, Frekuensi, Gaya, Gerak, Getaran, Kalor, Massa jenis, Medan magnet, Mekanika fluida, Momen Inersia, Panjang gelombang, Pemuaian, Percepatan (akselerasi), Radioaktif, Rangkaian listrik, Relativitas, Tekanan, Usaha Termodinamika, Vektor
- Bagaimana Albert Einstein mendapatkan rumus E=mc² ?
- Cara menjaga keluarga Anda aman dari teroris – Ahli anti-teror menerbitkan panduan praktis
- Apakah Anda Memerlukan Asuransi Jiwa? – Cara Memilih Asuransi Jiwa Untuk Pembeli Yang Pintar
- Ibu Hamil Dan Bahaya Kafein – Sayur & Buah Yang Baik Pada Masa Kehamilan
- Daftar Jenis Kanker: Pemahaman Kanker, Mengenal Dasar-Dasar, Contoh Kanker, Bentuk, Klasifikasi, Sel dan Pemahaman Penyakit Kanker Lebih Jelas
- Penyebab Dan Cara Mengatasi Iritasi Atau Lecet Akibat Pembalut Wanita
- Apakah Produk Pembalut Wanita Aman?
- Sistem Reproduksi Manusia, Hewan dan Tumbuhan
- Cara Mengenal Karakter Orang Dari 5 Pertanyaan Berikut Ini
- Kepalan Tangan Menandakan Karakter Anda & Kepalan nomer berapa yang Anda miliki?
Unduh / Download Aplikasi HP Pinter Pandai
Respons “Ooo begitu ya…” akan lebih sering terdengar jika Anda mengunduh aplikasi kita!
Siapa bilang mau pintar harus bayar? Aplikasi Ilmu pengetahuan dan informasi yang membuat Anda menjadi lebih smart!
Sumber bacaan: Math World, Popular Mechanics, Cliffs Notes
Pinter Pandai “Bersama-Sama Berbagi Ilmu”
Quiz | Matematika | IPA | Geografi & Sejarah | Info Unik | Lainnya | Business & Marketing